Dilatation du temps
Le terme dilatation du temps désigne un effet de la relativité restreinte selon lequel l'intervalle de temps entre deux événements mesurés dans un référentiel inertiel quelconque est toujours supérieur à l'intervalle de temps mesuré dans le référentiel inertiel (en mouvement relatif au premier) où ces deux événements ont la même position spatiale mais n'ont pas lieu au même moment[1].
Étant donné que le temps est défini, dans la théorie de la relativité, par la donnée initiale d'une horloge pour chaque référentiel[2],[3],[4], on peut en déduire que pour un observateur une horloge en mouvement semble ralentie par rapport à une horloge immobile[5]. Cet effet intervient sur tout mesureur du temps[6].
Un diagramme de Minkowski, en deux dimensions, permet une représentation de ce phénomène dans l'espace de Minkowski et peut aider à une compréhension qualitative et intuitive.
Ce phénomène de ralentissement des horloges s'étend, en relativité générale, à des référentiels non inertiels, et aussi, en raison du principe d’équivalence, à des points n’ayant pas le même potentiel gravitationnel : les horloges proches d'un corps massif vont ralentir par rapport à celles qui en sont plus éloignées.

Dessin de droite : ce même observateur voit passer à vitesse v une installation identique, il voit que la distance parcourue par la lumière entre le départ et le retour (qui n'ont pas lieu au même endroit) est 2*D et est supérieure à 2*L, mais la vitesse de la lumière est toujours c, même si la source lumineuse est en mouvement (postulat de la relativité restreinte). Pour lui, cet aller-retour dans l'installation en mouvement prend plus de temps que dans l'installation immobile.
Conclusion : le même phénomène prend plus de temps, donc paraît plus lent, quand il est vu en mouvement.
En relativité restreinte[modifier | modifier le code]
Exemple[modifier | modifier le code]
Considérons deux événements, par exemple l'émission de deux éclairs, par un appareil transporté par une fusée, et séparés par l'intervalle de temps Δτ mesuré dans cette fusée (c'est l'intervalle de temps propre les séparant car ces éclairs sont émis au même endroit pour la fusée). Chaque éclair est émis alors que la fusée passe devant un observateur terrestre différent lisant l'heure sur sa montre, et ces deux observateurs constatent que leurs lectures diffèrent du temps Δt . Comme la fusée se déplace à la vitesse v par rapport à la Terre, la distance entre ces deux observateurs terrestres concernés est de v Δt. Les deux mêmes événements « éclairs » étant séparés par l'intervalle d'espace-temps (Δx =vΔt, Δt ) dans le repère terrestre et (0, Δτ ) dans le repère de la fusée, la relativité restreinte affirme que le carré de l'intervalle d'espace-temps entre les deux événements est le même dans les deux repères et que de ce fait l'égalité suivante est respectée :
On en déduit:
avec
ce que l'on peut aussi obtenir par les transformations de Lorentz.
Ainsi, le temps propre mesuré dans la fusée est : le temps s'écoule plus lentement dans la fusée d'après les observateurs terrestres.
Cet effet est négligeable pour de faibles vitesses et c'est la raison pour laquelle la correction n'intervient pas dans la vie courante et que le phénomène n'est pas perceptible d'ordinaire. En revanche, dès qu'un objet atteint une vitesse de l'ordre du 1/10e de celle de la lumière, ou lorsque la précision demandée est importante, comme dans le cas d'un GPS, cet effet relativiste est notable et peut même devenir colossal, croissant sans limites, si v se rapproche tout près de la valeur c.
Vérifications expérimentales[modifier | modifier le code]
- Une vérification expérimentale a été menée en 1960 par les physiciens Robert Pound et Glen Rebka en accélérant des atomes par augmentation de la chaleur (les atomes restent sur place car ce sont les atomes d'un cristal radioactif vibrant autour de leur position d'équilibre par agitation thermique), ce qui a donné une diminution de la fréquence des rayons gamma émis (ce qui signifie un ralentissement du temps propre des atomes par rapport à celui des atomes non accélérés), les mesures étant en accord avec les prévisions avec 10 % de marge d'erreur[7].
- On a observé que les particules instables se désintègrent plus lentement du point de vue de l'observateur lorsqu'elles se meuvent à grande vitesse par rapport à celui-ci, notamment dans les accélérateurs de particules.
- Cet effet est également observé pour les muons atmosphériques produits par la collision des rayons cosmiques (particules très énergétiques en provenance de l'espace cosmique) et les molécules de l'atmosphère. Ces muons, animés d'une vitesse proche de celle de la lumière, atteignent le sol où ils sont observés et ce malgré leur courte durée de vie propre, la dilatation du temps leur donnant le temps nécessaire pour atteindre les détecteurs[8].
- Un autre cas observé de dilatation temporelle est le décalage entre horloges atomiques au sol et en vol ; mais il se complique dans ce dernier cas de considérations gravitationnelles de sorte que le cadre de la relativité restreinte est insuffisant et qu'on doit considérer les effets de relativité générale. Incidemment l'expérience réelle d'horloges atomiques embarquées en avion est une version réalisable, et souvent réalisée, de l'expérience des jumeaux, laquelle exploite l'effet de ralentissement des horloges en mouvement.
- Signalons également que l'on observe aussi une dilatation du temps lorsqu'on mesure la durée de l'évolution de la luminosité des supernovas lointaines, mais que ce dernier effet est dû à l'expansion de l'Univers.
Paradoxe apparent de la symétrie[modifier | modifier le code]
Le paradoxe des jumeaux[modifier | modifier le code]
Supposons qu'un observateur no 1 voie, depuis son référentiel inertiel muni d'une horloge (dite no 1) qui y est immobile, une horloge (dite no 2) en mouvement à vitesse constante comme fonctionnant au ralenti. Alors, par symétrie, un observateur no 2 immobile par rapport à l'horloge no 2 voit l'horloge no 1 comme étant en mouvement à vitesse constante par rapport à son référentiel (dit no 2) et donc comme fonctionnant au ralenti. Ainsi chacun voit l'horloge de l'autre comme fonctionnant au ralenti et voit également l'autre voyageur comme ayant subi une compression dans le sens de son déplacement. La contradiction est flagrante car si on imagine qu'ils se croisent deux fois : la première fois ils initialisent leurs deux horloges à 0, mais, la seconde fois, quelle horloge sera en retard par rapport à l'autre ?
L'explication la plus courante est que la contradiction n'est qu'apparente car pour qu'il y ait deux rencontres, une des deux horloges a dû changer de référentiel inertiel : la relativité restreinte s'y applique différemment et les calculs montrent que c'est cette horloge qui, à la seconde rencontre, retarde sur l'autre[7].
Réciprocité de la dilatation temporelle[modifier | modifier le code]
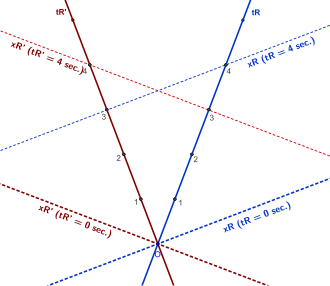
Dans le paradoxe des jumeaux, la dilatation temporelle est asymétrique et non réciproque car les deux référentiels en jeu ne sont pas galiléens. Mais si on considère deux référentiels galiléens, n'est-il pas paradoxal de considérer que chaque observateur dans son référentiel estime que le temps pour l'autre observateur passe plus lentement que pour lui ?
Cette situation peut être représentée par un diagramme de Minkowski symétrique (voir ci-contre). Chaque observateur (, et ) a synchronisé sa montre avec l'autre au point , et les deux observateurs s'éloignent ensuite l'un de l'autre à vitesse constante. Chaque observateur est immobile dans son propre référentiel et décrit une ligne d'univers droite dans l'espace de Minkowski ( et ). Supposons que chaque observateur a déclenché en un même processus physique censé durer quatre secondes. Chaque observateur constate, à sa propre horloge, que le phénomène a en effet duré quatre secondes. Ceci est la conséquence du principe de relativité : tout phénomène physique se déroule exactement de la même manière dans tout référentiel galiléen. Une seconde mesurée par dans le référentiel de est exactement égale à une seconde mesurée par dans le référentiel de [9],[note 1].
Ensuite, chaque observateur essaye de savoir combien de temps s'est passé pour l'autre observateur à la fin du processus. Les deux observateurs étant éloignés, ils ne peuvent comparer directement leurs horloges. Ils doivent donc estimer le temps dans l'autre référentiel simultané à la fin du processus dans le leur. Dans une vision présentiste de l'univers, l'observateur et son horloge possède une existence et un état réel à chaque instant du temps de , et réciproquement. L'horloge de l'autre observateur indique donc un temps bien défini au même moment que la fin du processus, qu'il s'agit de déterminer[9].
Mathématiquement, sur le diagramme de Minkowski, la droite de temps constant pour un référentiel donné est indiquée en pointillés. Cette droite représente une « photographie » en trois dimensions de l'univers à un instant donné dans un référentiel[note 2]. Dans l'espace de Minkowski, c'est la droite orthogonale à cet instant à la ligne d'univers du référentiel. Dans un espace euclidien deux droites orthogonales forment un angle de 90°, mais dans l'espace de Minkowski, approprié pour la relativité, l'angle dépend d'une certaine relation mathématique. On constate que, symétriquement, chaque observateur considère selon ce critère que moins de secondes se sont passées pour l'autre observateur (ici, 3 secondes au lieu de 4, le diagramme de Minkowski donne géométriquement les mêmes résultats que la transformation de Lorentz). Encore une fois, le principe de relativité est respecté : chaque observateur fait des observations similaires.

Mais n'est-ce pas paradoxal ? Qu'en est-il réellement ? Au même moment qui est le plus jeune ou le plus vieux ? Le paradoxe n'en est pas un si on considère que la notion de simultanéité elle-même est relative à un référentiel : c'est ce que l'on constate géométriquement sur le diagramme : chaque ligne de simultanéité pour chaque référentiel est clairement différente; c'est la conclusion à laquelle amène la théorie de la relativité. Le paradoxe n'apparaît que si on considère que la simultanéité est une notion absolue[9].
Une erreur fréquemment commise[10] est de considérer que le temps lui-même passe plus lentement dans le référentiel en mouvement et que les intervalles de temps mesurés dans le référentiel en mouvement seront toujours plus courts que ceux mesurés dans un référentiel fixe. D'une part, ce serait contraire au principe de relativité : chaque référentiel peut être considéré indifféremment fixe ou en mouvement. D'autre part, si on considère les intervalles de temps concernant des mêmes événements, l'estimation du temps écoulé entre deux mêmes événements pourra être plus courte, égale, ou plus longue dans chacun des référentiels, quel que soit leur état de mouvement. Par exemple l'intervalle de temps entre les événements A et B est plus longue dans , plus courte dans , entre B et C les intervalles sont égaux, et entre C et D, plus courte dans et plus longue dans (diagramme ci-contre). De plus les événements D et E sont simultanés dans mais ne le sont pas dans , alors que les événements D et F sont simultanés dans mais pas dans . La dilatation du temps est un phénomène causé par la relativité de la simultanéité et n'a rien à voir avec la façon dont le temps s'écoule[10].
Pour Carlo Rovelli, se poser la question des intervalles temporels quand on ne peut pas comparer directement les horloges n'a même pas de sens : « Si deux horloges se séparent et ne se rencontrent plus se demander laquelle est en avance et laquelle retarde n'a pas de sens. Si elles se rencontrent de nouveau, elles peuvent être comparées »[11].
En mouvement accéléré[modifier | modifier le code]
Contrairement à une idée répandue, la relativité restreinte ne s'arrête pas aux mouvements rectilignes uniformes mais est également capable de traiter des mouvements accélérés[12]. Ce qui fait la différence entre la relativité restreinte et la relativité générale, c'est qu'en relativité générale, on étend le concept de relativité au fait qu'il est impossible de distinguer masse inerte et masse pesante et donc, on ne peut pas non plus distinguer ponctuellement une accélération d'une attraction gravitationnelle. Pour cela, il devient nécessaire de sortir de la géométrie euclidienne ou plutôt minkovskienne qui décrivent des espaces sans courbure intrinsèque, pour passer à la géométrie différentielle avec les variétés de Lorentz. Toutefois, en relativité restreinte, il est possible d'étudier les effets d'un mouvement accéléré à partir des observations faites depuis un référentiel inertiel.
Pour comprendre les conséquences du mouvement accéléré sur la dilatation du temps, supposons une fusée qui contiendrait deux horloges, à l'avant et à l'arrière, qui chacune enverraient un signal lumineux toutes les secondes[13],[14].
Dans un référentiel accéléré (force appliquée à l'arrière de la fusée), chaque signal lumineux envoyé de l'avant vers l'arrière va aller à la rencontre de l'arrière de la fusée qui avance de plus en plus rapidement vers lui, alors que dans l'autre sens, les signaux lumineux venant de l'arrière vont eux, au contraire, devoir rattraper l'avant de la fusée qui lui, s'éloigne toujours plus vite de leur point d'émission.
Par conséquent les signaux allant de l'avant vers l'arrière vont donc à chaque fois parcourir une distance un peu plus courte pour atteindre leur cible, de sorte que, toujours dans le même référentiel inertiel, ils vont arriver à l'arrière à une cadence plus rapide que celle à laquelle ils ont été émis. Alors qu'au contraire, les signaux allant de l'arrière vers l'avant vont arriver à une cadence plus lente que leur cadence d'émission.
Pour les observateurs situés à l'avant et à l'arrière de la fusée, par contre, la lumière continue à se déplacer à la même vitesse indépendamment de leur propre mouvement, ce qui conduit à ce que pour eux c'est le temps qui ne s'écoule pas à la même vitesse entre l'avant et l'arrière de la fusée (notons au passage que cet exemple n'est pas tout à fait exact, car il ne prend pas en compte dans le référentiel inertiel, les déformations du temps et de l'espace subies par la fusée qui va de plus en plus vite).
En relativité générale[modifier | modifier le code]
Description du phénomène[modifier | modifier le code]
En relativité générale, un objet massif courbe l'espace-temps en le dilatant, dilatant ainsi le temps par rapport à un temps mesuré à distance de la déformation de l'espace-temps : si deux horloges sont identiques et que l'une a fait un séjour dans un champ de gravitation, alors elle retarde par rapport à l'autre. Cet effet se calcule grâce à la différence de potentiel gravitationnel entre deux points : le temps est dilaté là où le potentiel gravitationnel est le plus bas[15],[16] (en effet, par convention, le potentiel gravitationnel porte un signe négatif[17], et il peut être soit proche de 0, soit « profond »[16]). On mesure le temps dilaté en « minutes BNo », unité inventée par le physicien Robert Pound pour simplifier les calculs entre deux référentiels inertiels[réf. nécessaire].
Explication qualitative[modifier | modifier le code]
L'utilisation du principe d'équivalence entre accélération et gravitation sur l'exemple vu plus haut, de la fusée en accélération constante permet de prédire l'existence d'un même effet de dilatation temporelle entre le haut et le bas d'une tour jouant le rôle de l'avant et l'arrière de la fusée ou entre un satellite en orbite et le sol, comme c'est le cas pour le système GPS.
Contrairement à une croyance répandue [réf. souhaitée], la distorsion du temps entre deux points situés à des potentiels gravitationnels différents n'est pas directement liée aux variations de cette gravitation, mais est un effet cumulatif (dans le langage rigoureux de la théorie, il s'agit d'intégrer une forme différentielle)[18] lié à la pénétration vers le centre du champ gravitationnel, ce qui, par exemple, sur Terre, en fait essentiellement un corrélat de l'altitude (la variation de la gravitation due à cette altitude ajoutant une correction négligeable). Cet effet peut ainsi être présent entre deux points où la gravité est nulle, comme le montre l'exemple du centre de la Terre[19],[15].
Métrique de Schwarzschild[modifier | modifier le code]
On sait que la métrique est . Dans le cas d'une masse à symétrie sphérique, on peut utiliser la métrique de Schwarzschild[20]
où est le rayon de Schwarzschild de la masse sphérique, strictement inférieur au rayon .
On en déduit . Ainsi où est l'élément infinitésimal de temps propre du corps, et est celui du temps mesuré dans le référentiel de l'observateur, par hypothèse non soumis à la gravitation (sinon les formules sont différentes).
On peut dire que par la gravitation le temps propre est ralenti par rapport au temps du référentiel (qui est par hypothèse mesuré hors d'influence de la masse), ou que le temps impropre est dilaté par rapport au temps propre du corps influencé par la gravitation.
Cas d'un trou noir[modifier | modifier le code]
Dans le cas d'un trou noir, ici réduit à ses caractéristiques liées à la métrique, une horloge peut s'approcher du rayon de Schwarzschild du corps massif. En la supposant quasi immobile dans le référentiel, elle marque son temps propre , et le temps observé très loin du trou noir (à l'infini, pour faire court) est . Ce qui signifie qu'au fur et à mesure que l'horloge s'approche du rayon de Schwarzschild, le temps de l'horloge parait mettre un temps infini pour s'écouler aux yeux de l'observateur, et semble même s'arrêter à ses yeux, mais l'horloge ne s'arrête pas pour elle-même (comme la métrique de Lemaître ou celle de Kruskal et Szekeres le montrent).
Effets théoriques sur la Terre[modifier | modifier le code]
« Une horloge servant à chronométrer une rotation complète de la Terre mesurera environ 10 ns / jour de plus par jour pour chaque kilomètre d'altitude au-dessus du géoïde de référence. » (traduit de l'anglais : General relativity predicts that clocks run more slowly near massive objects. The effect is small — a clock at sea level lags behind one 1000 m above sea level by only 9.4 ns/day »)[21]. L'âge de la Terre se comptant en milliards d'années, l'effet est non négligeable : le calcul (effectué en 2016, en utilisant l'approximation newtonienne[22]) montre que le centre de la Terre est plus jeune de plus de deux ans que la surface[15]. En effet bien que la force de gravité y soit nulle[note 3], le centre de la Terre possède un potentiel gravitationnel une fois et demi plus important en valeur absolue[15] (Φ(0) = –3GM2R soit environ −94 MJ/kg) par rapport à celui en surface[15] (Φ(R) = –GMR soit environ[23] -63 MJ/kg).
Résultats expérimentaux[modifier | modifier le code]
En 1977, une expérience embarquant des horloges atomiques dans une fusée a confirmé les prévisions théoriques avec une précision de 0,01 %[24]. En 1959, Robert Pound et Glen Rebka ont pu vérifier expérimentalement que la différence d'altitude de 22,6 mètres d'une tour de l'université Harvard donnait une différence de fréquence de la lumière conforme aux prévisions de la relativité générale (expérience de Pound-Rebka mettant en évidence le décalage d'Einstein)[24],[25]. En 2009, une équipe de physiciens a mesuré avec une précision 10 000 fois supérieure à la précédente expérience (Gravity Probe A (en)) cette dilatation du temps sans déceler de différence avec les prédictions de la relativité générale[26],[27].
Combinaison des deux phénomènes[modifier | modifier le code]

Dans le cas des satellites artificiels en orbite circulaire, les deux effets relativistes (contraction due à la vitesse relative des deux repères et dilatation due à la plus faible valeur du champ gravitationnel) se combinent comme il est indiqué sur le graphique ci-contre.
Dans le cas de la synchronisation des satellites GPS, le temps propre du satellite doit être corrigé de −38 μs par jour principalement à cause de la relativité générale, le temps passant plus vite plus loin de la Terre, la position dans le champ gravitationnel étant plus élevée[28],[29].
Dans la fiction[modifier | modifier le code]
Dans le film Interstellar de Christopher Nolan, sorti en novembre 2014, est utilisé ce phénomène de dilatation du temps. L’astronaute Cooper voyage sur une exoplanète en orbite proche d'un trou noir supermassif (Gargantua). La force gravitationnelle du trou noir est si forte que le temps sur cette exoplanète s'écoule plus lentement avec un ratio de 1 heure pour 7 années terrestres[30].
Autres œuvres de fiction dans lesquelles la dilatation du temps joue un rôle important :
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Cela se traduit dans le diagramme de Minkowski par des graduations temporelles égales sur les axes et .
- Dans un diagramme de Minkowski, les trois dimensions de l'espace sont réduites à une dimension x
- Voir premier théorème de Newton.
Références[modifier | modifier le code]
- David Langlois, Introduction à la relativité : Principes fondamentaux et conséquences physiques, Vuibert, , 192 p., p. 16-19
- Premier paragraphe du §1 de Lev Landau et Evgueni Lifchits, Physique théorique, t. 2 : Théorie des champs [détail des éditions] :
- « Pour pouvoir décrire les phénomènes naturels il est nécessaire de définir un "système de référence" ou "référentiel". On entend par système de référence un système de coordonnées permettant d'indiquer les positions spatiales des particules auxquelles est liée une horloge marquant le temps. »
- Chapitre 2, §2.1.2, page 18 de Relativité et gravitation, par Philippe Tourrenc (Armand Colin éditeur, 1992, (ISBN 2 200 21209 7)) il est indiqué que « pour construire un système de coordonnées, nous mettons tout d'abord en place un certain nombre de « règles matérielles », dont une horloge « en chaque point de l'espace », qu'il faut « synchroniser », plus loin qu'« il faut utiliser des horloges « idéales » et que « tout cela est complexe, tant du point de vue pratique que conceptuel ».
- Chapitre 2, page 10 du cours de relativité restreinte de Pierre Billoir :
- « il faut préciser une méthode opérationnelle pour établir un repérage de l'espace et du temps, dont des horloges indéréglables, qu'on synchronise. »
- « Le temps propre d'un objet mobile est toujours inférieur à l'intervalle de temps correspondant dans un système fixe; on peut dire qu'une horloge mobile marche plus lentement qu'une horloge fixe » dans le §3 de Lev Landau et Evgueni Lifchits, Physique théorique, t. 2 : Théorie des champs [détail des éditions].
- p. 6 du cours de relativité générale par Bernard Linet, il est indiqué, avant tout postulat sur l'espace et le temps, qu'un observateur possède une horloge (et une règle graduée, le tout pour explorer son environnement) et que c'est un fait d'expérience que tous les phénomènes périodiques, classiques ou quantiques, donnent le même temps t.
- D'après James H. Smith, Introduction à la relativité, chez Masson édition de 1997, page 101 (chapitre "le paradoxe des jumeaux")
- Marc Vincent, « Validation des principes de la relativité restreinte », sur Ressources scientifiques pour l'enseignement de la physique, ENS Lyon,
- Vesselin Petkov, Relativity and the Nature of Spacetime, (œuvre littéraire), Springer Science+Business Media, p. 143-145
- (en) Tatsu Takeuchi, An illustrated Guide to Relativity, Cambridge University Press, , p. 138
- Carlo Rovelli, L'ordre du temps, Flammarion, (ISBN 978-2-08-140920-0) Chapitre 3 Note 7
- (en) Charles W. Misner, Kip S. Thorne et John Archibald Wheeler, Gravitation, New York, W. H. Freeman, , 1279 p. (ISBN 0-7167-0334-3, 9780716703341 et 0716703440, OCLC 585119, lire en ligne), Chap 6, pp.163 et suivantes
- (en) Richard P. Feynman, Robert B. Leighton et Matthew L. Sands, The Feynman lectures on physics : New millenium edition. Volume II, Mainly electromagnetism and matter (ISBN 978-0-465-07998-8, 0465079989 et 9780465072972, OCLC 861525314, lire en ligne), Chap. 42: Curved Space
- Analyse de Richard Feynman, Leçons sur la Physique page 315
- Uggerhøj, Mikkelsen et Faye 2016.
- (en) Proceedings of the International Conference on Two Cosmological Models, Plaza y Valdes (ISBN 978-607-402-530-9, lire en ligne), page 26
- (en) Comprehensive Physics XI, Laxmi Publications (ISBN 978-81-7008-733-5, lire en ligne), page 876
- Relativité Générale: La gravitation en une leçon et demie, conférence X-UNS-EPS de Marios Petropoulos, 2017
- Le noyau de la Terre vieillit moins vite que nous, sur Futura-sciences.
- (en) Charles Misner, Kip Thorne et John Archibald Wheeler, Gravitation, New York, Freeman, , 1279 p. (ISBN 0-7167-0334-3), p. 820
- « Measurement of gravitational time dilation: An undergraduate research project », American Journal of Physics,
- L'approximation newtonienne est légitime dans tous les cas où la gravitation est faible et les vitesses petites par rapport à celle de la lumière. Voir Lev Landau et Evgueni Lifchits, Physique théorique, t. 2 : Théorie des champs [détail des éditions] §81 et §82.
- (en) « Gravitational Potential | S-cool, the revision website », sur www.s-cool.co.uk (consulté le )
- Jean-Claude Boudenot, chapitre VI p. 145 à p. 147 de Électromagnétisme et gravitation relativiste, édité chez ellipse en 1989, (ISBN 2-7298-8936-1).
- (en) R. V. Pound, « Gravitational Red-Shift in Nuclear Resonance », Physical Review Letters, vol. 3, no 9, 1e november 1959, p. 439–441 (DOI 10.1103/PhysRevLett.3.439, lire en ligne, consulté le )
- Laurent Sacco, Retard des horloges : un test donne – encore – raison à Einstein sur Futura-sciences
- (en) Holger Müller, « A precision measurement of the gravitational redshift by the interference of matter waves », Nature, vol. 463, , , 926-929 (DOI 10.1038/nature08776, lire en ligne, consulté le )
- Gary Dagorn, « Comment la théorie de la relativité d'Einstein a changé nos vies », Le Monde, (lire en ligne)
- Does gravitational time dilation happen due to height or difference in the strength of the field?
- « Décryptez la physique des trous noirs du film Interstellar », (consulté le )
Annexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Lev Landau et Evgueni Lifchits, Physique théorique, t. 2 : Théorie des champs [détail des éditions]
- [Uggerhøj, Mikkelsen et Faye 2016] (en) U. I. Uggerhøj, R. E. Mikkelsen et J. Faye, « The young centre of the Earth », Eur. J. Phys., vol. 37, no 3, (DOI 10.1088/0143-0807/37/3/035602, Bibcode 2016EJPh...37c5602U, arXiv 1604.05507).
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- (fr)Traduction du texte Zur Elektrodynamik bewegter Kör-per, publié en 1905 par Albert Einstein : « De l'électrodynamique des corps en mouvement » [PDF], sur classiques.uqac.ca,





















![{\displaystyle \mathrm {d} t={\frac {\mathrm {d} \tau }{\sqrt {1-{\frac {R_{S}}{r}}}}}{\xrightarrow[{r\to R_{S}}]{}}\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fde24bdfcfd554bb5b7301f43016c73f5c07e04a)