Vitesse de libération
| Unités SI | mètre par seconde |
|---|---|
| Dimension | L·T −1 |
| Nature | Grandeur scalaire extensive |
| Symbole usuel | ou |
| Lien à d'autres grandeurs |
La vitesse de libération, ou vitesse d'évasion ou d'échappement est, en physique, la vitesse minimale que doit atteindre un projectile pour échapper définitivement à l'attraction gravitationnelle d'un astre (planète, étoile, etc.) dépourvu d'atmosphère et s'en éloigner indéfiniment. Cette vitesse est d'autant plus importante que la masse de l'astre est importante et que l'objet est proche de son centre. Relative à l'astre, c'est une valeur scalaire (sa direction ne joue aucun rôle). Cette vitesse est supérieure à la vitesse de satellisation minimale nécessaire pour que l'objet puisse se placer en orbite autour de l'astre.
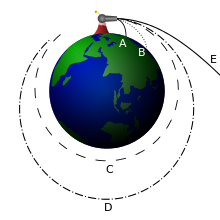
Si la vitesse de satellisation minimale correspond à la vitesse nécessaire pour maintenir une orbite circulaire juste au-dessus de l'atmosphère, l'augmentation de cette vitesse rend la trajectoire de plus en plus elliptique et la vitesse de libération correspond au point où la trajectoire cesse d'être une ellipse pour devenir une parabole avant de devenir une hyperbole.
Pour un objet lancé depuis la surface de la Terre, la vitesse de libération lui permettant d'échapper à l'attraction terrestre est de 11,2 km/s (soit 40 320 km/h). Par comparaison la vitesse de satellisation minimale autour de la Terre est de 7,9 km/s (soit 28 440 km/h). Les vitesses de libération depuis la surface du Soleil, de la Lune et de Mars sont respectivement de 617,5 km/s, 2,4 km/s et 5 km/s. Une fois qu'un objet a échappé à l'attraction terrestre, il reste, comme la Terre, soumis à l'attraction du Soleil. La vitesse de libération lui permettant d'échapper à cette attraction est de 42,1 km/s (soit 151 560 km/h).
Même si une sonde spatiale est libérée de l'attraction terrestre, elle doit disposer d'un surcroît de vitesse lui permettant de modifier son orbite autour du Soleil pour atteindre un autre corps céleste.
Contrairement aux projectiles qui suivent des trajectoires balistiques, un objet capable d'une accélération permanente serait, lui, théoriquement capable d'échapper à l'attraction dès le moment où il peut dépasser la vitesse de satellisation minimale, en suivant une trajectoire en spirale.
Caractéristiques[modifier | modifier le code]
La vitesse de libération (ou vitesse d'évasion) est la vitesse minimale à communiquer à un projectile pour que celui-ci échappe à l'attraction du champ de gravité d'un astre (planète, étoile, etc.) et atteigne un point à l'infini. À cette vitesse, la trajectoire de l'objet devient une parabole qui s'éloigne de l'astre vers l'infini. En dessous de cette vitesse, l'objet reste lié à la planète : il suit une orbite elliptique autour de l'astre ou, si sa vitesse est inférieure à la vitesse de satellisation minimale, il s'écrase sur l'astre[1],[2],[3].
De façon générale, pour un objet placé dans un champ de gravité d'un astre (possédant une symétrie sphérique de la répartition de sa masse, une approximation généralement valable pour une planète ou une lune d'un diamètre supérieur à quelques centaines de km), la vitesse de libération prend la valeur suivante :
avec :
- est la constante gravitationnelle : ;
- est la masse de l'astre ;
- est le rayon de l'astre ;
- est la distance de l'objet à la surface de l'astre ;
- est le paramètre gravitationnel standard associé à la masse de l'astre : .
Propriétés[modifier | modifier le code]
La vitesse de libération d'un astre augmente lorsque la masse de l'astre (M) augmente ou lorsque son rayon (R) diminue. Plus l'astre est massif ou dense, plus la vitesse de libération est importante.
L'objet qui doit atteindre la vitesse de libération s'il est placé en altitude (d > 0) requiert une vitesse de libération inférieure à celle d'un objet placé à la surface de l'astre.
La vitesse de libération est une quantité scalaire et non vectorielle : elle spécifie juste une amplitude, pas une direction. Un objet qui se déplace à la vitesse de libération peut échapper au champ de gravitation quelle que soit sa direction initiale (dans la mesure où la trajectoire ne rencontre pas la surface de l'astre). Elle ne dépend pas non plus de la masse de l'objet, seulement de celle de l'astre.
De manière usuelle la vitesse de libération est calculée pour un objet posé à la surface de l'astre (au niveau des océans en ce qui concerne la Terre). Elle peut être également calculée pour un objet placé en orbite autour de l'astre comme une sonde spatiale orbitant autour du Soleil.
La vitesse de libération d'un objet posé à la surface d'un astre en rotation comme la Terre dépend de la direction dans laquelle il est lancé et de la latitude du site de lancement. En effet l'objet posé à la surface est entraîné par la rotation de l'astre et cette vitesse vient en diminution ou en augmentation de la vitesse de libération. À l'équateur de la Terre un objet lancé vers l'est dans une direction tangente à l'équateur bénéficie dès le départ d'un surcroît de vitesse 465 m/s : sa vitesse de libération théorique est de 10,735 km/s au lieu de 11,2 km/s. La vitesse de rotation de la surface décroît comme le cosinus de la latitude : à la latitude de Baïkonour (46°) la réduction de la vitesse de libération n'est plus que de : 465 m/s × cos(46°) = 323 m/s. Si l'engin spatial est lancé vers l'ouest la vitesse de libération est augmentée d'autant.
La vitesse de libération est, par ailleurs, la vitesse minimale à laquelle un objet situé à l'infini et animé d'une vitesse initiale nulle atteindra la surface de l'astre. Une météorite s'écrasant sur un astre dépourvu d'atmosphère comme Mercure percutera la surface au minimum à la vitesse de libération de cette planète (4,3 km/s). Dans le cas de la Terre la vitesse de la météorite sera plus ou moins réduite (en fonction de sa taille, forme) par l'atmosphère avant de percuter le sol.
En pratique un lanceur chargé de lancer une sonde spatiale à une vitesse de libération doit également prendre en compte les frottements de l'atmosphère de l'astre et compenser les forces exercées par le champ gravitationnel durant son ascension. Ces paramètres dépendent des caractéristiques de l'astre et nécessitent, par exemple pour la Terre, pourvue d'une atmosphère épaisse et dense, d'ajouter environ 2 km/s.
Calcul[modifier | modifier le code]
Par application du principe de la conservation d'énergie[modifier | modifier le code]
Le calcul de la vitesse de libération peut être effectué en utilisant le principe de la conservation de l'énergie. On se place dans un référentiel galiléen lié à l’astre créant le champ gravitationnel, et on suppose que l’objet n'est soumis qu'à la force gravitationnelle qui est une force conservative. Dans ce référentiel l'énergie mécanique du corps est constante au cours du temps.
L'énergie mécanique du corps plongé dans un champ gravitationnel est la somme de son énergie cinétique et de son énergie potentielle avec :
- → Énergie cinétique d'un corps de masse m se déplaçant à la vitesse v
- → Énergie potentielle d'un corps de masse m à une distance D de l'astre de forme approximativement sphérique de masse M dans son champ de gravitation
Par l'énergie mécanique d'un corps situé à une distance infinie de l'astre[modifier | modifier le code]
L'énergie mécanique d'un corps animé exactement de la vitesse de libération par rapport à un astre est calculée en deux points de sa trajectoire : dans sa position initiale (notée pi) lorsqu'il se trouve dans le champ gravitationnel de l'astre à une distance R de celui-ci et dans sa position finale (pf) lorsqu'il se trouve à une distance infinie de l'astre et qu'il a échappé à l'attraction de celui-ci.
Dans sa position finale (pf) :
- la vitesse du corps est nulle par définition de la vitesse de libération, donc l'énergie cinétique est nulle
- l'énergie potentielle dans le champ de gravitation de l'astre est nulle puisque l'objet a échappé à celui-ci
Détermination de la vitesse de libération[modifier | modifier le code]
En application de la loi de la conservation de l'énergie, l'énergie mécanique de l'objet dans ses positions initiale et finale est identique :
Si la position initiale, pi, se trouve à la surface de la planète, c'est-à-dire si est égal au rayon de celle-ci, la vitesse du corps correspondant à la vitesse de libération est donc celle qui satisfait à l'équation :
Les masses m se simplifient et on obtient ainsi la vitesse de libération.
Vitesse de libération par rapport à plusieurs astres[modifier | modifier le code]
La vitesse de libération d'un objet placé au repos dans un champ gravitationnel comportant plusieurs sources dérive de l'énergie potentielle cumulée en ce point par rapport à l'infini. L'énergie potentielle est obtenue simplement en cumulant les énergies potentielles de chaque astre. La vitesse de libération théorique est égale à la racine carrée de la somme des carrés des vitesses de libération par rapport à chaque astre. Ainsi la vitesse de libération théorique d'un objet placé à la surface de la Terre pour qu'il échappe à la fois à l'attraction de la Terre et du Soleil est :
avec
- 11,2 km/s vitesse de libération par rapport à la Terre d'un objet au repos à la surface de Terre
- 42,1 km/s vitesse de libération par rapport au Soleil d'un objet au repos situé au niveau de l'orbite de la Terre autour du Soleil.
Cas des vitesses proches de celle de la lumière[modifier | modifier le code]
Ce calcul n'est valable que pour les vitesses de libération très inférieures à la vitesse de la lumière puisque l'on utilise une approximation de l’énergie cinétique valable uniquement pour les faibles vitesses. Dans les domaines où elle est appliquée généralement (mouvement des astres ou des engins spatiaux), cette approximation est suffisante.
Calcul avec le champ de gravitation de surface[modifier | modifier le code]
Soit une planète de masse M et de rayon R. On suppose ici qu'elle ne tourne pas sur elle-même.
Soit un corps de masse m à la surface de cette planète.
À toute distance r du centre, tout corps subit une force attractive
À la surface, on exprime alors , g le champ gravitationnel d'expression
Le travail fourni pour déplacer un corps d'une distance contre cette force valant ,
le travail total nécessaire pour déplacer le corps de la surface de la Terre à l'infini vaut:
Afin d'atteindre l'infini, l'énergie cinétique minimale du corps au départ doit égaler ce travail, donc la vitesse de libération vl satisfait
d'où le résultat:
C'est là la vitesse de libération à la surface de la Terre. En remplaçant R par R + h, on obtient la vitesse de libération pour toute altitude h.
Cas des objets en accélération constante[modifier | modifier le code]
La vitesse d'un corps pour maintenir une orbite circulaire à une distance du corps autour duquel il orbite, est la vitesse pour laquelle la force d'échappement centrifuge est égale à la force d'attraction gravitationnelle . Cette vitesse (qui se calcule en résolvant l'équation ) est égale à et diminue avec la distance (Ce qui est logique, sinon cela signifierait que les corps situés à des distances arbitrairement grandes continuent à s'attirer de façon non négligeable).
Par conséquent, un corps en orbite circulaire qui accélérerait, même très légèrement de façon constante verrait son orbite s'agrandir en spirale jusqu'au moment où il atteindrait un rayon orbital pour lequel la vitesse de libération est égale à sa vitesse instantanée, et où il finirait par s'échapper.
Ceci n'est cependant pas réellement utilisable en trajectoire spatiale, car cela impliquerait des trajectoires extrêmement longues.
Exemples de vitesses de libération[modifier | modifier le code]

La vitesse de libération d'un corps quittant la surface de la Terre, dite aussi deuxième vitesse cosmique, est de l'ordre de 11,2 km/s (soit environ 40 000 km/h) par rapport à un référentiel inertiel géocentrique. Par comparaison, celle de Jupiter est de 59,5 km/s. Un objet ayant échappé à l'attraction gravitationnelle de la Terre se trouve placé dans le champ gravitationnel du Soleil : si sa vitesse est égale à celle de la vitesse de libération de la Terre il va circuler sur une orbite héliocentrique (autour du Soleil) quasi identique à celle de la Terre. Pour que cet objet puisse quitter le Système solaire c'est-à-dire échapper à l'attraction du Soleil, il doit atteindre la troisième vitesse cosmique, qui est de l'ordre de 42,1 km/s par rapport à un référentiel inertiel héliocentrique (c'est-à-dire si l'objet reste fixe par rapport au Soleil ce qui correspond à une situation uniquement théorique) et de 16,6 km/s par rapport à un référentiel géocentrique (lié à la Terre) c'est-à-dire si l'objet circule sur une orbite héliocentrique identique à celle de la Terre. Le système solaire est lui-même en orbite autour du centre de notre galaxie, la Voie lactée. Un objet échappant à l'attraction du Soleil se trouvera donc en orbite autour de la Voie lactée.
Le tableau suivant recense quelques exemples de vitesses de libération nécessaires pour échapper à l'attraction de certains objets.
| Objet posé à la surface de1 |
Pour échapper à l'attraction de |
Vitesse de libération (Ve) (km/s) |
Objet situé au niveau de l'orbite de |
Pour s'échapper à l'attraction de |
Vitesse de libération si objet statique2 |
Vitesse de libération si objet circule sur une orbite héliocentrique |
|---|---|---|---|---|---|---|
| Soleil | Soleil | 617,5 | ||||
| Mercure | Mercure | 4,3 | Mercure | Soleil | 67,7 | |
| Vénus | Vénus | 10,3 | Vénus | Soleil | 49,5 | |
| Terre | Terre | 11,2 | Terre | Soleil | 42,1 | 16,6 |
| Lune | Lune | 2,4 | Lune | Terre | 1,4 | |
| Mars | Mars | 5 | Mars | Soleil | 34,1 | |
| Jupiter | Jupiter | 59,5 | Jupiter | Soleil | 18,5 | |
| Ganymède | Ganymède | 3 | ||||
| Saturne | Saturne | 35,6 | Saturne | Soleil | 13,6 | |
| Uranus | Uranus | 21,2 | Uranus | Soleil | 9,6 | |
| Neptune | Neptune | 23,6 | Neptune | Soleil | 7,7 | |
| Pluton | Pluton | 1 | ||||
| Système solaire | Voie lactée | ~1 000 | ||||
| 1Pour les planètes gazeuses, la surface est définie par certaines conventions (pour Jupiter pression atmosphérique = 1 bar) 2Situation théorique : un objet sans vitesse serait précipité vers le Soleil | ||||||
Applications[modifier | modifier le code]

Du fait de la présence de l'atmosphère terrestre, il est difficile (et peu utile) d'amener un objet proche de la surface de la Terre à la vitesse de libération qui atteint 11,2 km/s. Cette vitesse qui relève du régime hypersonique est trop élevée pour pouvoir être atteinte dans l'atmosphère terrestre avec un système de propulsion ; en outre, un objet atteignant cette vitesse à basse altitude serait détruit par les forces de friction. En pratique, un objet qui doit être lancé depuis la Terre à une vitesse de libération (sonde spatiale) accélère progressivement en traversant les couches denses de l'atmosphère avant d'atteindre l'orbite terrestre basse (160 à 2 000 km d'altitude) puis est accéléré à partir de cette altitude, jusqu'à dépasser 11,2 km/s dans le référentiel géocentrique.
D'un point de vue historique la sonde spatiale soviétique Luna 1, conçue pour survoler la Lune et lancée en 1959, a été le premier objet artificiel à atteindre la vitesse de libération terrestre. Certaines sondes spatiales soviétiques du programme Luna et les modules lunaires du programme Apollo ont décollé du sol lunaire et échappé à l'attraction de celle-ci.
Les vaisseaux du programme Apollo n'ont pas eu besoin d'atteindre tout à fait la vitesse de libération de la Terre, puisque la Lune se trouve dans le champ d'attraction de la Terre.
Enfin plusieurs sondes spatiales de la NASA (Pioneer 10, Pioneer 11, Programme Voyager, New Horizons) disposent d'une vitesse suffisante pour échapper à l'attraction du Soleil dans quelques dizaines de milliers d'années. Aucun lanceur existant n'est suffisamment puissant pour lancer une sonde spatiale de quelques centaines de kg à une vitesse de libération lui permettant d'échapper à l'attraction du Soleil. Ces missions ont dû avoir recours à l'assistance gravitationnelle de planètes pour atteindre la vitesse nécessaire.
Vitesse de libération et trou noir[modifier | modifier le code]
Comme pour tout corps céleste, la vitesse de libération aux abords d'un trou noir varie suivant la distance à son centre (quelle que soit la métrique utilisée). Les différentes métriques permettant une description du passage du rayon de Schwarzschild montrent que la vitesse de libération au-delà du rayon de Schwarzschild est strictement inférieure à la vitesse de la lumière ; sur ce rayon, on peut dire qu'elle est égale à la vitesse de la lumière, bien que cela ne permettrait que de se mettre en satellite sans pouvoir s'éloigner ; et en deçà du rayon, elle est strictement supérieure à la vitesse de la lumière et tout corps est alors irrémédiablement en chute vers le centre du trou noir.
Notes et références[modifier | modifier le code]
- Entrée « vitesse de libération », dans Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Bruxelles, De Boeck Université, , XI-672 p. (ISBN 978-2-8041-5688-6, BNF 41256105), p. 524, en ligne sur Google Livres (consulté le 21 juillet 2014)
- Entrée « vitesse de libération » sur FranceTerme, la base de données terminologiques de la délégation générale à la langue française et aux langues de France du ministère de la Culture (France) (consulté le 21 juillet 2014)
- Michel Capderou (préface de Gérard Mégie), Satellites : Orbites et missions, Paris, Springer, , 486-XVI p. (ISBN 2-287-59772-7, BNF 38943828, lire en ligne), p. 23, en ligne sur Google Livres (consulté le 21 juillet 2014)
- « Solar System Data », Georgia State University
- (en) « 1959-012A », NASA - National Space Science Data Center
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Vitesses cosmiques, calculées par Constantin Tsiolkovski
- Vitesse de satellisation minimale
- Delta-v
- Vitesse orbitale
- Assistance gravitationnelle