Périapside
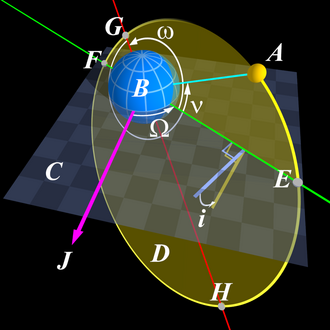
Le périapse, la périapside, l’apside inférieure ou le péricentre est le point de l’orbite d’un objet céleste où la distance est minimale par rapport au foyer de cette orbite (point G dans l’image ci-contre).
Le terme périastre désigne normalement la périapside (terme général) d'une orbite décrite autour d'une étoile. Selon les corps en orbite, le mot change, bien que le terme périapside reste toujours admissible. On parle alors de :
- périhélie pour une orbite décrite autour du Soleil ;
- périgée pour la Terre ;
- périsélène ou périlune pour la Lune ;
- périgalacticon pour le centre d'une galaxie ;
- etc.
L'antonyme de périapside est apoapside, apoapse ou apocentre (point H dans l’image ci-contre).
Ces deux points extrêmes (périapse et apoapse) sont désignés ensemble sous le terme générique d’apsides.
Dans le cas particulier de la Terre, une confusion est à éviter :
- si on se réfère à son orbite autour du Soleil, on parlera de périhélie ;
- si on se réfère à l’orbite de ses satellites (naturel ou artificiel) autour d’elle, on parlera de périgée.
La distance du centre de masse (foyer de l’orbite) au périapse peut se calculer de la façon suivante :
où est la longueur du demi grand axe de l’orbite et est l’excentricité orbitale.
Formules détaillées[modifier | modifier le code]
Les formules suivantes caractérisent le périapse et l’apoapse d’un objet quelconque :
- Périapse :
- vitesse (maximale) du corps orbital à son périapse :
- distance du périapse (minimale) au centre de masse (foyer de l’orbite) :
- Apoapse :
- vitesse (minimale) du corps orbital à son apoapse :
- distance de l’apoapse (maximale) au centre de masse (foyer de l’orbite) :
Selon les lois de Kepler sur le mouvement des planètes (conservation du moment cinétique) et les principes de la conservation de l’énergie, les quantités suivantes sont constantes pour une orbite donnée :
où :
- est la longueur du demi grand axe ;
- est le paramètre gravitationnel standard (produit de la constante gravitationnelle G par la masse M du corps central) ;
- est l’excentricité orbitale définie par
Attention : pour convertir la distance mesurée depuis les surfaces des objets en distance mesurée depuis les centres de gravité, il faut ajouter le rayon des objets en orbite ; et réciproquement.
La moyenne arithmétique des deux distances extrêmes est la longueur du demi grand axe de l’ellipse orbitale. La moyenne géométrique de ces deux mêmes distances est la longueur du demi petit axe de l’ellipse orbitale.
La moyenne géométrique des deux vitesses limites , est la vitesse correspondant à une énergie cinétique qui, à n’importe quelle position sur l’orbite, ajoutée à l’énergie cinétique courante, permettrait à l’objet en orbite de s’échapper de l’attraction. La racine carrée du produit des deux vitesses est donc la valeur locale de la vitesse de libération.
Terminologie[modifier | modifier le code]
| Corps central | Périapside |
|---|---|
| Galaxie | Périgalacticon |
| Trou noir | Périmélasme[1] Péribothron[2] |
| Étoile | Périastre |
| Soleil | Périhélie |
| Mercure | Périherme |
| Vénus | Péricythère |
| Terre | Périgée |
| Lune | Périsélène |
| Mars | Périarée |
| Jupiter | Périzène |
| Saturne | Périkrone |
| Uranus | Périourane |
| Neptune | Périposéide |
| Pluton | Périhade |
Dans le cas d’une étoile et des principaux objets du système solaire, un terme spécialisé apparenté peut être employé comme indiqué dans le tableau ci-contre.
Toutefois, seuls périhélie, périgée et périastre sont couramment utilisés. Ces termes sont formés en prenant la racine grecque du corps central correspondant.
Les termes périlune (pour un satellite d’une lune) et périjove (pour un satellite de Jupiter) sont à éviter.
On voit parfois aussi le terme péricynthe dans le cas d’un satellite artificiel de la Lune.
Le terme « péripluto », préconisé par certains auteurs peut également être utilisé comme un équivalent à « périhade ».
Source[modifier | modifier le code]
- Droit français : arrêté du relatif à la terminologie des sciences et techniques spatiales.
Notes et références[modifier | modifier le code]
- « Orbites des objets célestes (Apsides) », sur Astronoo (consulté le ).
- « La meilleure image réalisée à ce jour d’un nuage de poussière passant à proximité du trou noir du centre de la Galaxie - Des observations du VLT confirment que G2 a survécu à son approche et consiste en un objet compact », sur www.eso.org, (consulté le ).



























