Équation de Kepler

En astronomie, l'équation de Kepler est une formule liant, dans une orbite, l'excentricité e et l'anomalie excentrique E à l'anomalie moyenne M. L'importance de cette équation est qu'elle permet de passer des paramètres dynamiques du mouvement d'un astre (l'anomalie moyenne) aux paramètres géométriques (l'anomalie excentrique). Cette équation a été établie par Kepler dans le cas des orbites elliptiques, en analysant les relevés de position de la planète Mars effectués par Tycho Brahe. Elle fut ensuite généralisée aux autres formes d'orbites (paraboliques, hyperboliques, quasi-paraboliques, rectilinéaires) à l'aide des principes de la mécanique newtonienne.

Présentations de l'équation de Kepler

L'équation de Kepler en tant que telle est celle établie par Kepler pour les orbites elliptiques. Elle peut cependant être déclinée en plusieurs formes pour couvrir tous les cas d'orbites.

Cas de l'orbite elliptique

L'équation de Kepler en orbite elliptique est :

$E-e\cdot \sin {(E)}=M$

avec l'anomalie moyenne M définie par :

$M=n\cdot (t-t_{0})$

avec n le moyen mouvement :

$n={\frac {2\cdot \pi }{T}}$

t le temps et t₀ étant l'instant du passage au périastre. T est la période orbitale.

Démonstration

Schéma permettant de trouver graphiquement l'équation de Kepler.

Sa démonstration est simple et fait appel au calcul de l'aire d'un secteur d'ellipse, dont le sommet est occupé par un des deux foyers, par deux méthodes différentes, dont l'une faisant appel à la loi des aires et l'autre en calculant l'aire de ce secteur elliptique projeté sur le cercle principal de l'ellipse.

D'après la seconde loi de Kepler, l'aire balayée par le segment SP sur le schéma est proportionnel au temps. Donc l'aire du secteur elliptique SzP est égal à k(t – t₀), où t est le temps et t₀ est l'instant du passage de l'astre en z. La constante de proportionnalité k peut être déterminée facilement : au bout d'une période orbitale T, l'aire balayée sera égale à l'aire totale de l'ellipse πab (a et b étant le demi grand axe et demi petit axe de l'ellipse), soit :

$SzP={\frac {\pi ab}{T}}(t-t_{0})$

Il reste à déterminer l'aire du secteur d'ellipse SzP géométriquement pour faire le lien entre le temps écoulé depuis le passage en z et la position sur l'orbite.

Kepler a utilisé pour cela un cercle auxiliaire circonscrit à l'ellipse (l'aire d'un secteur circulaire étant facile à connaître).

L'aire du secteur Szx est égale à la différence du secteur circulaire czx et du triangle cSx. $Szx=czx-cSx={\frac {1}{2}}a^{2}\cdot E-{\frac {1}{2}}a^{2}\cdot e\cdot \sin(E)$

où E est exprimé en radians.

Finalement, SzP = Szx×b/a : l'un étant une compression de l'autre du rapport b/a (où plus précisément, une affinité de rapport b/a) On obtient l'équation de Kepler, après simplification, en explicitant l'égalité SzP = k(t – t₀), soit :

${\frac {2}{ab}}SzP={\frac {2\pi }{T}}(t-t_{0})=E-e\cdot \sin(E)$

Le moyen mouvement peut être aussi exprimé par :

$n={\sqrt {\frac {G\cdot \ (m_{1}+m_{2})}{a^{3}}}}$

où

• G est la constante universelle de la gravitation
• m₁ et m₂ les masses des deux corps
• a le demi-grand axe de l'ellipse $a={\frac {p}{1-e^{2}}}$ ; p étant le paramètre de l'ellipse

L'équation de Kepler, associée au lien entre l'anomalie excentrique E et l'anomalie vraie v

$\tan {(v/2)}={\sqrt {\frac {1+e}{1-e}}}\cdot \tan {(E/2)}$

permet de déterminer la position au cours du temps d'un astre sur son orbite.

Cas de l'orbite hyperbolique

En cas d'orbite hyperbolique (e > 1), on peut démontrer analytiquement une relation équivalente à l'équation de Kepler :

$e\cdot \sinh {(H)}-H=M$

où sinh désigne le sinus hyperbolique.

M est défini de la même manière que dans le cas elliptique, avec l'expression du moyen mouvement suivant :

$n={\sqrt {\frac {G\cdot \ (m_{1}+m_{2})}{(-a)^{3}}}}$

L'argument H n'est plus un angle comme c'est le cas de E dans le mouvement elliptique. H est dans ce cas liée à l'anomalie vraie v par :

$\tan {(v/2)}={\sqrt {\frac {e+1}{e-1}}}\cdot \tanh {(H/2)}$

Cas de l'orbite parabolique

L'équation de Kepler n'est pas définie dans le cadre du mouvement parabolique (e = 1). Elle est remplacée par l'équation de Barker.

$M=s+{\frac {s^{3}}{3}}$

avec

$~s=\tan {(v/2)}$

$M=n\cdot (t-t_{0})$ et

$n=2\cdot {\sqrt {\frac {G\cdot \ (m_{1}+m_{2})}{p^{3}}}}$

Cette équation cubique peut être résolue de manière analytique par la méthode de Cardan.

Expression universelle de l'équation de Kepler

Par un changement de variable, les équations de Kepler elliptiques, paraboliques et hyperboliques peuvent être regroupées en une seule équation "universelle". Une des expressions possible est :

$qx+ex^{3}c_{3}(\alpha x^{2})={\sqrt {G\cdot \ (m_{1}+m_{2})}}(t-t_{0})$

avec le périastre q = a(1-e), et α = 1/a. α est positif pour les orbites elliptiques, nul pour les orbites paraboliques et négatif pour celles hyperboliques. La nouvelle variable x est définie par :

$x=E\cdot {\sqrt {a}}$

et la fonction c₃(t) est une des fonctions de Stumpff, qui s'écrit dans le cas général :

$c_{k}(t)=\sum _{n=0}^{+\infty }{\frac {(-1)^{n}}{(2n+k)!}}t^{n}$

Démonstration

En partant de l'équation elliptique,

$E-e\cdot \sin {(E)}={\sqrt {\frac {\mu }{a^{3}}}}(t-t_{0})$

avec

$\mu =G\cdot \ (m_{1}+m_{2})$

et en procédant au changement de variable

$x=E\cdot {\sqrt {a}}$

on obtient

$ax-ea{\sqrt {a}}\cdot \sin {\left({\frac {x}{\sqrt {a}}}\right)}={\sqrt {\mu }}(t-t_{0})$

Avec le développement en série du sinus, on trouve :

$\sin \left({\frac {x}{\sqrt {a}}}\right)={\frac {x}{\sqrt {a}}}-{\frac {x^{3}}{a{\sqrt {a}}}}\sum _{n=0}^{+\infty }{{\frac {(-1)^{n}}{(2n+3)!}}{\left({\frac {x^{2}}{a}}\right)}^{n}}$

L'équation de Kepler se transforme en :

$qx+ex^{3}\sum _{n=0}^{+\infty }{{\frac {(-1)^{n}}{(2n+3)!}}{(\alpha x^{2})}^{n}}={\sqrt {\mu }}(t-t_{0})$

La discontinuité sur a pour les orbites paraboliques a été supprimée, et l'expression de a n'apparait plus sous une racine carré, rendant utilisable cette équation aussi pour les orbites hyperbolique. La formule obtenue en partant de l'équation de Kepler hyperbolique serait en tout point équivalente à celle-ci en posant $x=iH\cdot {\sqrt {a}}$.

La détermination de x d'après l'équation universelle permet de déterminer la position du corps sur son orbite (X,Y) par :

$X=a(\cos {E}-e)=q+a\cdot \cos {\left({\frac {x}{\sqrt {a}}}\right)}=q-x^{2}\sum _{n=0}^{+\infty }{{\frac {(-1)^{n}}{(2n+2)!}}{(\alpha x^{2})}^{n}}=q-x^{2}c_{2}(\alpha x^{2})$

$Y=a{\sqrt {1-e^{2}}}\sin {E}={\sqrt {a(1-e^{2})}}{\sqrt {a}}\sin {\left({\frac {x}{\sqrt {a}}}\right)}=x\cdot {\sqrt {q(1+e)}}\sum \limits _{n=0}^{+\infty }{{\frac {(-1)^{n}}{(2n+1)!}}{(\alpha x^{2})}^{n}}=x\cdot {\sqrt {q(1+e)}}c_{1}(\alpha x^{2})$

Les fonctions c₁(t) et c₂(t) étant définies de la même manière que c₃(t) plus haut.

Orbites rectilinéaires

Les orbites rectilinéaires sont des cas limites des autres orbites, en faisant tendre la distance au périastre q vers zéro tout en conservant le demi grand axe a constant : l'orbite tend alors vers un segment ou une demi-droite. Pour le cas des orbites elliptiques et hyperboliques, cela suppose de faire tendre l'excentricité e vers 1, car demi grand axe a, excentricité e et périastre q sont liés par q = a(1–e). Il existe donc trois types d'orbites rectilinéaires : elliptiques, paraboliques et hyperboliques. En pratique, une partie seulement de ces orbites est décrite par l'astre, aboutissant soit à une collision, soit à une évasion. Certaines comètes kamikazes détectées par les observatoires solaires spatiaux (SoHO, SDO…) ou bien des tronçons d'orbites de sondes interplanétaires sont proches des orbites rectilinéaires.

Pour l'orbite rectilinéaire elliptique, l'équation de Kepler devient :

$~E-\sin {(E)}=M$

avec l'anomalie moyenne M définie par :

$~M=n\cdot (t-t_{0})$

L'anomalie vraie n'ayant plus de signification pour une orbite rectilinéaire, la position de l'astre est définie par sa distance le séparant de l'astre principal r:

$~r=a(1-\cos {(E)})$

Pour l'orbite rectilinéaire hyperbolique, l'équation de Kepler devient :

$~\sinh {(H)}-H=M$

et la position de l'astre :

$~r=a(1-\cosh {(H)})$

a étant négatif pour les orbites hyperboliques

Enfin, pour l'orbite rectilinéaire parabolique :

$M={\frac {s^{3}}{6}}$

avec

$~M=n\cdot (t-t_{0})$ et

$n={\sqrt {G\cdot \ (m_{1}+m_{2})}}$

et la position de l'astre :

$r={\frac {s^{2}}{2}}$

Résolution de l'équation de Kepler

L'équation de Kepler

$E-e\cdot \sin {(E)}=M$

permet de calculer de manière directe la date (liée à M) correspondant à une position donnée (liée à E), par exemple déterminer la date des équinoxes. Par contre le problème inverse, déterminer la position d'une planète pour une date donnée, nécessite la détermination de E, connaissant M et e. Ce problème ne peut pas être résolu de manière simple.

Résoudre l'équation de Kepler, c'est trouver E(e,M) :

• comme série de Fourier puisque c'est une fonction périodique impaire de M
• comme série entière de e, si e < e₀ := 0,6627..., rayon de convergence de la série.
• comme une valeur numérique avec un nombre de chiffres (d), pour un temps de calcul tc(d) optimisé.

Série de Fourier

C'est Lagrange qui trouve l'expression, bien que le nom J_n(x) soit associé au nom de Bessel.

• E – M est une fonction impaire périodique de M :

$E-M=e\cdot \sin E=2\cdot \sum _{n=1}^{+\infty }{\frac {J_{n}(ne)}{n}}\sin(nM)$

où J_n(x) est la fonction de Bessel de 1^re espèce d'ordre n.

Démonstration

E – M est une fonction continue, impaire et périodique de période 2π ; elle est donc développable en série de Fourier, dont les coefficients des cosinus sont tous nuls.

$E-M=e\cdot \sin E=\sum _{p\geq 1}b_{p}\sin(pM)$

avec

$b_{p}={\frac {1}{\pi }}\int _{0}^{2\pi }e\sin(E)\sin(pM)~\mathrm {d} M$

Pour changer la variable d'intégration, on intègre par parties, en posant u = sin(E) et dv = sin(pM) dM, on obtient :

$b_{p}={\frac {e}{p\pi }}\int _{0}^{2\pi }\cos(E)\cos(pM)~\mathrm {d} E$

En transformant le produit de cosinus en somme de cosinus, on obtient :

$b_{p}={\frac {e}{p}}\left({\frac {1}{2\pi }}\int _{0}^{2\pi }\cos[(1+p)E-ep\sin(E)]~\mathrm {d} E+{\frac {1}{2\pi }}\int _{0}^{2\pi }\cos[(1-p)E+ep\sin(E)]~\mathrm {d} E\right)$

après avoir remplacé dM par (1–e cos E )dE (égalité obtenue en dérivant l'équation de Kepler).

Or, les fonctions de Bessel de première espèce s'expriment par :

$J_{p}(x)={\frac {1}{2\pi }}\int _{0}^{2\pi }\cos[pE-x\sin(E)]~\mathrm {d} E$

d'où :

$b_{p}={\frac {e}{p}}[J_{p+1}(pe)+J_{p-1}(pe)]$

Par ailleurs, les fonctions de Bessel vérifient la relation de récurrence :

$J_{p-1}(x)+J_{p+1}(x)={\frac {2p}{x}}J_{p}(x)$

d'où finalement :

$b_{p}={\frac {2}{p}}J_{p}(pe).$

Série entière de l'excentricité

C'est encore Lagrange qui trouve la solution, que Laplace complétera en donnant le rayon de convergence. Ces travaux inspireront Cauchy, qui fondera la théorie des séries analytiques pour résoudre ce problème épineux ; celui-ci verra son aboutissement avec les travaux de Puiseux.

L'application du théorème d'inversion de série de Lagrange fournit :

$E-M=\sum _{n=1}^{+\infty }{e^{n} \over n!}\cdot a_{n}(M)$

avec

$\ a_{n}(M)={\mathrm {d} ^{n-1} \over {\mathrm {d} M^{n-1}}}(\sin ^{n}M).$

Le rayon de convergence minimum de la série, qui dépend de M, est atteint pour M = π/2, et vaut e₀ = 0,6627434193 tel qu'indiqué par Laplace (1823) et démontré par Cauchy et Puiseux :

$e_{0}=2{\frac {\sqrt {x(1-x)}}{1-2x}}$ et x tel que ${\frac {1-x}{x}}=\exp \left({\frac {2}{1-2x}}\right)$.

Ceci rend cette formule inapplicable pour déterminer la position des comètes, dont l'excentricité est souvent voisine de 1.

Les premiers termes sont :

$E-M=e\cdot \sin M+e^{2}\cdot \sin M\cdot \cos M+e^{3}\cdot \left(\sin M\cdot \cos ^{2}M-{\sin ^{3}M \over 2}\right)+\dots$

Note : il est possible d'obtenir ce développement en série en remplaçant dans la série de Fourier précédente les fonctions de Bessel par leur développement limité :

$J_{n}(x)=(x/2)^{n}\sum _{p=0}^{\infty }{(-1)^{p} \over p!(n+p)!}(x/2)^{2p}$

On obtient alors le développement limité beaucoup plus simplement que par la méthode de l'inversion de série :

$E-M=$

$\left(e-{\frac {e^{3}}{8}}+{\frac {e^{5}}{192}}+\cdots \right)\cdot \sin M+\left({\frac {e^{2}}{2}}-{\frac {e^{4}}{6}}+{\frac {e^{6}}{48}}+\cdots \right)\cdot \sin 2M+\left({\frac {3}{8}}e^{3}-{\frac {27}{128}}e^{5}+\cdots \right)\cdot \sin 3M$

$+\left({\frac {e^{4}}{3}}-{\frac {4}{15}}e^{6}+\cdots \right)\cdot \sin 4M+\left({\frac {125}{384}}e^{5}+\cdots \right)\cdot \sin 5M+\left({\frac {27}{80}}e^{6}+\cdots \right)\cdot \sin 6M$

Il est à noter que bien que la série de Fourier converge pour 0 < e < 1, et que les développements des fonctions de Bessel aient un rayon de convergence infini, le résultat après réorganisation des termes ne converge que pour e < 0,662...

Cas des comètes : e > e₀

Le premier à se confronter au problème est Horrocks, puis surtout Halley, pour les calculs sur sa comète d'excentricité e = 0,9673.

Plusieurs solutions ont été proposées en modifiant légèrement l'équation de Barker (e = 1). La solution proposée par Bessel (1805) couvre le domaine e > 0,997. Gauss s'illustra en donnant une belle solution pour 0,2 < e < 0,95.

Une généralisation de l'équation de Barker est un développement en série convergeant d'autant plus rapidement que l'excentricité e est proche de 1, ce qui s'avère bien adapté aux cas des comètes (cette série s'applique aussi aux orbites légèrement hyperboliques) :

$n(t-t_{0})=S+(1-2\gamma ){\frac {S^{3}}{3}}-\gamma (2-3\gamma ){\frac {S^{5}}{5}}+\gamma ^{2}(3-4\gamma ){\frac {S^{7}}{7}}-\ldots =S+\sum _{p=1}^{\infty }(-\gamma )^{p-1}\left(p-(p+1)\gamma \right){\frac {S^{2p+1}}{2p+1}}$

qui a pour rayon de convergence : $|\gamma |S^{2}<1$

avec S = tan(v/2)

$n={\frac {k}{2}}{\frac {\sqrt {1+e}}{q^{3/2}}}$

$\gamma ={\frac {1-e}{1+e}}$

v étant l'anomalie vraie, k la constante gravitationnelle de Gauss, e et q étant respectivement l'excentricité et le périastre de l'orbite, t le temps et t₀ étant l'instant du passage au périastre.

Lorsque e = 1, la série se réduit à l'équation de Barker.

Démonstration

La première loi de Kepler stipule que les orbites sont des sections coniques (ellipses, paraboles ou hyperbole) ayant le soleil pour foyer. Donc la distance comète - soleil r et l'anomalie vraie v sont liées par l'équation d'une conique en coordonnées polaires :

$r={\frac {p}{1+e\cos v}}$

où p et e sont respectivement le paramètre de l'excentricité de la conique.

La deuxième loi de Kepler (le segment soleil-comète balaye des aires égales en des temps égaux) peut être exprimée, en considérant un intervalle de temps dt infiniment petit :

$r^{2}{\frac {\mathrm {d} v}{\mathrm {d} t}}=h$

où h est une constante, appelée constante des aires.

En combinant ces deux équations, on peut faire disparaître r, pour obtenir le lien entre le temps et l'anomalie vraie, c'est-à-dire une forme de l'équation de Kepler s'appliquant à tout type d'orbite.

$\left({\frac {p}{1+e\cos {v}}}\right)^{2}dv=h~\mathrm {d} t$

soit en intégrant entre t₀ et t :

${\frac {h}{p^{2}}}(t-t_{0})=\int _{0}^{v}{\frac {1}{{(1+e\cos {x}})^{2}}}~\mathrm {d} x$

en changeant la variable d'intégration s = tan(x/2), et en posant S = tan(v/2), on transforme cette intégrale trigonométrique en intégrale de fonction rationnelle :

${\frac {h(1+e)^{2}}{2p^{2}}}(t-t_{0})=\int _{0}^{S}{\frac {1+s^{2}}{{(1+\gamma s^{2}})^{2}}}~\mathrm {d} s.$

La fonction rationnelle peut être intégrée directement pour obtenir toutes les formes des équations de Kepler vues plus haut, dépendant du signe de γ. Mais en développant la fraction rationnelle en série entière de s, puis en intégrant terme à terme cette série, on obtient :

${\frac {h(1+e)^{2}}{2p^{2}}}(t-t_{0})=\int _{0}^{S}{\frac {1+s^{2}}{{(1+\gamma s^{2}})^{2}}}~\mathrm {d} s=\int _{0}^{S}1+\sum _{p=1}^{\infty }(-\gamma )^{p-1}\left(p-(p+1)\gamma \right)s^{2p}~\mathrm {d} s=S+\sum _{p=1}^{\infty }(-\gamma )^{p-1}\left(p-(p+1)\gamma \right){\frac {S^{2p+1}}{2p+1}}$

les relations entre le paramètre de la conique et la constante des aires,

$p=a(1-e^{2})=q(1+e)={\frac {h^{2}}{G(m_{1}+m_{2})}}$

permet de retrouver la formule cherchée (en négligeant la masse m₂ de la comète vis-à-vis de celle du soleil).

Calcul numérique

L'équation de Kepler peut être résolue à l'aide d'un algorithme de recherche d'un zéro d'une fonction. Les méthodes du type encadrement, méthode de dichotomie, méthode de la fausse position nécessitent un encadrement de départ dans lequel la racine est présente. Du fait de la périodicité et la parité de l'équation de Kepler, il est toujours possible de ramener l'intervalle de départ à [0 , π]. Ceci fournit un encadrement de départ pour ces méthodes, mais il est aisé d'en trouver de plus fins.

Les méthodes du type point fixe nécessitent une estimation de départ de la racine, le germe de la méthode E₀, pour lancer les calculs : il en existe de multiples dans la littérature, dont la plus simple est E₀ = M.

La méthode de type point fixe la plus simple, celle utilisée par Kepler, est :

$E_{0}=M~$

$E_{n+1}=M+e\cdot \sin E_{n}{\text{ pour }}n=0,1\ldots$

converge lentement lorsque e est proche de 1. Il est alors avantageux de lui adjoindre un algorithme d'accélération de la convergence : le Delta-2 de Aitken, par exemple, ou la variante de Steffensen.

L'équation de Kepler se prête particulièrement bien aux algorithmes nécessitant le calcul des dérivées successives élevées, du fait du faible coût en calcul machine nécessaire. En effet :

$f(E)=E-e\cdot \sin E-M$

$f'(E)=1-e\cdot \cos E$

$f''(E)=e\cdot \sin E$

$f'''(E)=e\cdot \cos E$

Les dérivées suivantes se déduisant cycliquement des précédentes. Les variantes de la méthode de Newton et de Halley d'ordres plus élevés sont donc très performantes dans ce cas. Il est à noter que ces méthodes peuvent dans certains cas avoir des difficultés à converger (e proche de 1 et M proche de 0). Il est préférable dans ces zones soit de proposer une valeur de départ moins grossière (germe de Mikkola (Seppo Mikkola) ou de Markley), soit de brider les méthodes itératives pour les forcer à converger (modification de Hamming de la méthode de Newton), ou d'utiliser des méthodes itératives à convergence moins locale (méthode de Laguerre).

Exemple

Lors de son dernier passage en 1986, la comète de Halley a eu la visite de la sonde Giotto. Les données nécessaires pour déterminer la position de la comète lors de cette rencontre sont:

• date du passage au périhélie t₀ : 9 février 1986 à 10:59:55 UTC
• date de la rencontre t : 14 mars 1986 à 00:03:00 UTC, soit t – t₀ = 32,54328 jours
• excentricité de l'orbite e : 0,96727426
• distance au périhélie q : 0,58710224, soit le demi grand axe a = q/(1–e) = 17,940753 et le moyen mouvement n = k/a^1,5 = 0,0002263836 rad/jour.

L'anomalie moyenne vaut M =n (t – t₀) = 0,0073673887 rad

L'équation de Kepler à résoudre est :

$E-0,96727426\sin(E)=0,0073673887$

En partant de E₀ = M et en utilisant la méthode de Newton,

Graphique représentant le nombre d’itérations (de noir=0 à blanc=255 ou plus) nécessaires à la méthode de Newton pour résoudre l'équation de Kepler avec une valeur initiale égale à M. Pour chaque couple (e,M), la couleur du point indique le nombre d'itérations

$E_{n+1}=E_{n}-{\frac {E_{n}-e\cdot \sin E_{n}-M}{1-e\cdot \cos E_{n}}}$

on trouve successivement :

0,0073673887

0,2249486948

0,1929911041

0,1909186907

0,1909107985

0,1909107984

… (les valeurs suivantes étant identiques) On en déduit l'angle de position de la comète sur son orbite (l'anomalie vraie) v = 1,2771772327 rad = 73,176865125°

La distance de la comète au soleil se calcule par r = a(1 – e cos(E)) = 0,902374257 UA (légèrement inférieure à la distance terre-soleil)

La vitesse de la comète vaut $v=42.1219{\sqrt {1/r-1/(2a)}}$ soit 43,780 8 km/s

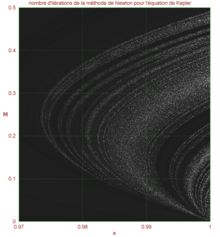
Les itérations ne se passent pas toujours aussi bien pour les comètes, comme l'expose le graphique ci contre. Pour des excentricités au-delà de 0.97, la convergence est incertaine avec comme point de départ des itérations E₀ = M. D'autres points de départ plus précis permettent d'éviter cet écueil.

Dans le cas des comètes, la résolution de la généralisation quasi-parabolique de l'équation de Barker pose deux problèmes :

• le calcul approché de la série qui peut nécessiter un grand nombre de termes, voire être impossible si elle diverge. Il se trouve que cette série se prête particulièrement bien à l'utilisation d'algorithmes d'accélération de la convergence, notamment le Δ² de Aitken ou l'ε-algorithme de Peter Wynn, qui non seulement accélèrent la convergence, mais étendent son domaine de convergence. En pratique, les difficultés interviennent lorsque la comète est très loin de son périastre (elle est alors depuis longtemps invisible), ou son excentricité diffère notablement de 1 (dans ce cas, il est plus judicieux de résoudre l'équation de Kepler elliptique ou hyperbolique).
• La résolution de l'équation proprement dite. Celle-ci peut être effectuée par les méthodes de type Newton avec :

$F(S)=-n(t-t_{0})+S+\sum _{p=1}^{\infty }(-\gamma )^{p-1}\cdot (p-(p+1)\cdot \gamma )\cdot {\frac {S^{2p+1}}{2p+1}}$

en remarquant que la dérivée s'exprime simplement :

$F'(S)={\frac {1+S^{2}}{{(1+\gamma \cdot S^{2})}^{2}}}$

les dérivées suivantes s'en déduisent facilement.

On pourra choisir comme valeur initiale de l'itération S₀, la solution de l'équation cubique obtenue en retenant les premiers termes (différant légèrement de l'équation de Barker), à l'aide de la méthode de Cardan

$n(t-t_{0})=S_{0}+(1-2\cdot \gamma )\cdot {\frac {{S_{0}}^{3}}{3}}.$

Recherches actuelles

Les calculs via les intégrateurs symplectiques exigent de rester toujours en butée du nombre de décimales, dans le moindre coût de calcul. Elle dépend beaucoup du doublet (M,e), M compris entre 0 et π et de e, surtout quand ce dernier paramètre est voisin de 1.

Nijenhuis (1991) adopte la méthode de Mikkola (1987) qui est la méthode de Newton d'ordre 4, en choisissant « adéquatement » le germe E₀ en fonction du doublet (M,e).

Il est clair que dans les calculs numériques, le volume de calculs est essentiel, autant que le nombre de décimales, vu l'instabilité du système solaire évaluée à un coefficient de Liapunov de 10^{(t/5 Myr)}. On se heurte à une muraille exponentielle : difficile d'aller plus loin que 25 Myr, même avec un traitement 128 bits.

Ce sont ces calculs (astronomiques... mais informatisés) qui tournent sur les machines de l'IMCCE-Paris. Le calcul de l'ensoleillement terrestre à la latitude 65° Nord, I(65,t) est calculé et on essaie d'en déduire la corrélation avec le climat passé : l'échelle géologique jusqu'au néogène (25 M ans) en est déduite (échelle géologique Gradstein 2004). Prochaine étape prévue : les 65 M ans.

Histoire des sciences

Avant Kepler, l'équation était déjà étudiée pour d'autres motifs :

c'est le problème de la réduction des coordonnées locales aux coordonnées géocentriques : il faut réduire la correction de parallaxe. Habash al Hasib s'y est déjà attaqué.

Avant 1700, il y a déjà beaucoup de tentatives : Kepler naturellement, Curtz (1626), Niele, Boulliau (1645, 1657), Seth Ward (1653), Paganus (1657), Horrebow (1717), Cassini (1669), Newton (1665?), Wren (1658), Wallis (1659), Jeremiah Horrocks (1638)...

Bibliographie

• (en) Peter Colwell, Solving Kepler's equation over three centuries, Richmond, Va, Willmann-Bell, 1993, 202 p. (ISBN 978-0-943-39640-8, OCLC 28724376)
• (en) John Brinkley, Trans Roy Irish Ac, vol. 7, 1803, p. 321-356
• (en) Jean Meeus, Astronomical algorithms, Richmond, Va, Willmann-Bell, 1991, 429 p. (ISBN 978-0-943-39635-4, OCLC 24067389)
• (en) Albert Nijenhuis (de), « Solving Kepler's Equation with high efficiency and accuracy », Celest. Mech. Dyn. Astron., vol. 51,‎ 1991, p. 319-330 (lire en ligne)
• (en) Seppo Mikkola, « A cubic approximation for Kepler's equation », Celest. Mech. Dyn. Astron., vol. 40,‎ 1987, p. 303–312 (lire en ligne)

Voir aussi

Articles connexes

• Équation du centre
• Mouvement képlérien
• Astronomia nova
• Fonction de Stumpff

Liens externes

• [OI] (en) « Kepler's equation » [« équation de Kepler »], notice d'autorité n^o 20110803100034177 de l'Oxford Index (OI), dans la base de données Oxford Reference de l'Oxford University Press (OUP).
• (en) Série d'articles de Danby et Burkardt[1][2]
• (en) Algorithme et programme de calcul par Odell et Gooding [3]
• (en) La méthode de Gauss pour la résolution de l'équation de Kepler
• Notices d'autorité :

  • BnF (données)
  • IdRef
  • LCCN