0,999…

(«  »)

Est-ce une représentation de 1 ?

En mathématiques, le développement décimal périodique qui s'écrit $\scriptstyle 0,999\ldots$, que l'on dénote encore par $\scriptstyle 0,{\bar {9}}$, $\scriptstyle 0,{\dot {9}}$ ou $\scriptstyle 0,(9)$ représente un nombre réel dont on peut montrer que c'est le nombre 1. En d'autres termes, les deux notations $\scriptstyle 0,999\ldots$ et $\scriptstyle 1$ sont deux notations différentes pour le même nombre. Les démonstrations mathématiques de cette identité ont été formulées avec des degrés variés de rigueur mathématique, selon les préférences pour la définition des nombres réels, les hypothèses sous-jacentes, le contexte historique et le public visé.

Le fait que certain nombres réels peuvent être représentés par plus d'une chaîne de « décimales » n'est pas limité au système décimal, c'est-à-dire de base 10. Le même phénomène a lieu dans toutes les bases entières, et les mathématiciens ont aussi repéré la manière d'écrire 1 dans des systèmes à base non-entière. Ce phénomène n'est d'ailleurs pas spécifique au nombre 1 : tout nombre décimal non-nul dont l'écriture est finie a une autre écriture avec une infinité de 9, comme $\scriptstyle 8,32=8,31999\ldots$ L'écriture avec un nombre fini de décimales est plus simple, et est presque toujours celle que l'on préfère, ce qui contribue au préjugé que c'est la « seule » représentation. Cependant, l'autre forme, avec une infinité de décimales, est parfois plus utile pour la compréhension du développement décimal de certaines fractions, ou, en base 3, pour la structure de l'ensemble de Cantor ternaire, une fractale simple. La forme non-unique doit être prise en compte dans la démonstration classique de ce que l'ensemble des entiers n'est pas dénombrable. Plus généralement, tout système de représentation numérique positionnelle pour les nombres réels contiennent une infinité de nombres ayant des représentations multiples.

L'égalité $\scriptstyle 0,999\ldots =1$ a longtemps été acceptée par les mathématiciens et enseignée dans les manuels. Ce n'est que dans les dernières décennies que les chercheurs en enseignement des mathématiques ont étudié comment les élèves admettaient cette égalité. Certains la rejettent, en raison de leur intuition que chaque nombre a un développement décimal unique, qu'il doit y avoir des nombres infinitésimaux non-nuls, ou bien que le développement $\scriptstyle 0,999\ldots$ finit par se terminer. Ces intuitions n'ont pas lieu d'être dans le système des nombres réels, mais il existe d'autre systèmes de nombres qui peuvent en admettre certaines. Dans certains cadres, il y a des nombres qui « évitent » 1 ; ces systèmes sont en général sans connexion avec le problème de $\scriptstyle 0,999\ldots$, mais ils peuvent être d'un intérêt considérable pour l'analyse mathématique.

Démonstrations algébriques

Fractions et divisions indéfinies

Une raison pour l'existence de développement décimaux indéfinis est la nécessité de représenter les fractions dans le système décimal. En utilisant les divisions indéfinies, une simple division d'entiers telle que $\scriptstyle 1/9$ donne un développement décimal infini $\scriptstyle 0,111\ldots$ dans lequel les décimales se répètent sans fin. Cette égalité donne une démonstration rapide de ce que $\scriptstyle 0,999\ldots =1$.

En effet, il suffit de multiplier les deux membres de la relation $\scriptstyle 1/9=0,111\ldots$ par 9, pour obtenir d'une part $\scriptstyle 9\times (1/9)=1$ et $\scriptstyle 9\times (0,111\ldots )=0,999\ldots$ Ces deux nombres sont donc bien égaux. Sous une autre forme, on peut multiplier $\scriptstyle 1/3=0,333\ldots$ de part et d'autre par 3

${\begin{aligned}\scriptstyle {\frac {1}{3}}&\scriptstyle =0,333\ldots \\[-1ex]\scriptstyle 3\times {\frac {1}{3}}&\scriptstyle =3\times 0,333\ldots \\[-1ex]\scriptstyle 1&\scriptstyle =0,999\ldots \end{aligned}}$

Manipulation des décimales

Quand un nombre en notation décimale est multiplié par 10, les chiffres ne changent pas, mais le séparateur des unités est décalé d'un cran vers la droite.
Donc $\scriptstyle 10\times 0,999\ldots =9,999\ldots$ , ce qui est le nombre original plus 9, ce qui se voit aisément par soustraction, toutes les décimales se soustrayant l'une de l'autre pour donner 0. La suite demande un tout petit peu d'algèbre :

${\begin{aligned}\scriptstyle x&\scriptstyle =0,999\ldots \\[-1ex]\scriptstyle 10x&\scriptstyle =9,999\ldots \\[-1ex]\scriptstyle 10x-x&\scriptstyle =9,999\ldots -0.999\ldots \\[-1ex]\scriptstyle 9x&\scriptstyle =9\\[-1ex]\scriptstyle x&\scriptstyle =1\\[-1ex]\scriptstyle 0,999\ldots &\scriptstyle =1\end{aligned}}$

Discussion

Bien que ces démonstrations montrent que $\scriptstyle 0,999\ldots =1$, la mesure où elles apportent une explication compréhensible dépend du public. Au début de l'arithmétique, ce genre de démonstration peut servir à montrer pourquoi $\scriptstyle 0,999\ldots =1$ et pourquoi $\scriptstyle 0,333\ldots <0,4$. Au début de l'algèbre, ces démonstrations aident à montrer pourquoi la méthode générale de conversion entre fractions et développements décimaux périodiques marche. Mais ces démonstrations ne donnent pas beaucoup de lumière sur les relations fondamentales entre les arrangements décimaux et les nombres qu'ils représentent, ce qui est le fondement de la question selon laquelle deux développements décimaux différents représentent ou non le même nombre. William Byers pense qu'un élève qui admet que $\scriptstyle 0,999\ldots =1$ à cause des démonstrations précédentes, mais qui n'a pas résolu l'ambiguïté, ne comprend pas vraiment l'équation. Fred Richman pense que le premier argument « tire sa force du fait que les gens ont été conditionnés à accepter la première ligne sans y réfléchir. ».

Une fois qu'un schéma de représentation est défini, il peut être utilisé pour justifier les règles d'arithmétique décimale utilisées dans les démonstrations précédentes. De plus, on peut démontrer directement que les expressions $\scriptstyle 0,999\ldots$ et $\scriptstyle 1.000\ldots$ représentent toutes deux le même nombre réel, car cela fait partie de la définition (voir infra).

Démonstrations analytiques

Puisque la question de $\scriptstyle 0,999\ldots$ ne pose pas de problème pour le développement formel des mathématiques, on peut en reculer le traitement jusqu'à avoir une démonstration solide de l'analyse réelle. Un des préalables est de caractériser les nombres réels qui peuvent être écrits en notation décimale, par un signe optionnel, une suite finie de chiffres formant en général la partie entière, un séparateur décimal et une suite de chiffres formant en général une partie fractionnaire. Si l'on veut discuter de $\scriptstyle 0,999\ldots$, on va se borner à des positifs, pour lesquels il n'est pas besoin d'écrire un signe, et une représentation quelconque a la forme :

$\scriptstyle b_{0},b_{1}b_{2}b_{3}b_{4}b_{5}\ldots$

Il est essentiel que la « partie entière » $\scriptstyle b_{0}$ ait un nombre fini de chiffres, et par contre que la « partie fractionnaire » ne soit en rien limitée à un nombre fini, même grand, de chiffres. Ceci est entendu en notation positionnelle, au sens où le 5 de 500 vaut dix fois le 5 de 50, et le 5 de 0,05 vaut un dixième de celui de 0,5.

Séries et suites infinies

L'extension peut-être la plus courante des développements décimaux est de les définir comme des séries infinies. En général :

$\scriptstyle b_{0},b_{1}b_{2}b_{3}b_{4}b_{5}\ldots \,=\,b_{0}+b_{1}/10+b_{2}/10^{2}+b_{3}/10^{3}+b_{4}/10^{4}+b_{5}/10^{5}+\ldots$

Pour $\scriptstyle 0,999\ldots$ on peut appliquer le théorème de convergence des séries géométriques  :

Si $\scriptstyle |r|<1$ , alors $\scriptstyle ar+ar^{2}+ar^{3}+\ldots =ar/(1-r).$

Comme $\scriptstyle 0,999\ldots$ est une somme de ce genre, avec $\scriptstyle r=1/10$, le théorème liquide la question :

$\scriptstyle 0,999\ldots =9/10+9/10^{2}+9/10^{3}+\ldots =(9/10)/(1-1/10)=1$

Cette démonstration (en fait celle que $\scriptstyle 9,999\ldots \,=\,10$) apparaît dès 1770 dans les « Éléments d'algèbre » de Leonhard Euler.

Limites : l'intervalle unité, avec la suite des fractions (en base 4) : $\scriptstyle 0,3~;~0,33~;~0,333~;~\ldots$ convergeant vers 1.

En fait la sommation de la série géométrique en soi est un résultat plus ancien qu'Euler. Une démonstration typique du XVIII^e siècle utilisait une une manipulation terme à terme analogue à la démonstration algébrique donnée plus haut, et le manuel de Bonnycastle « Introduction à l'algèbre », encore en 1811, utilise ce genre d'argument pour justifier $\scriptstyle 0,999\ldots =1$. Une réaction du XIX^e siècle contre ce genre de méthodes de sommation cavalières a résulté dans la définition encore dominante aujourd'hui : la somme d'une série est « définie » comme la limite de la suite de ses sommes partielles. Une démonstration dans ce cadre calcule explicitement la suite des sommes partielles ; on peut la trouver dans toute introduction aux fonctions ou à l'analyse, basée sur la démonstration.

Une suite $\scriptstyle (x_{0},~x_{1},~x_{2},~\ldots ~)$ admet une limite $\scriptstyle x$ si la distance $\scriptstyle |x\,-\,x_{n}|$ devient arbitrairement petite quand $\scriptstyle n$ s'accroît. L'affirmation que $\scriptstyle 0,999\ldots \,=\,1$ peut être interprétée et démontrée comme une limite :

$\scriptstyle 0,999\ldots =\lim _{n\to \infty }0,\underbrace {\scriptstyle 99\ldots 9} _{\scriptstyle n}=\lim _{n\to \infty }\sum _{k=1}^{n}{\frac {9}{10^{k}}}=\lim _{n\to \infty }\left(1-{\frac {1}{10^{n}}}\right)=1-\lim _{n\to \infty }{\frac {1}{10^{n}}}=1\,$

La dernière étape – le fait que $\scriptstyle \lim _{n\to \infty }{\frac {1}{10^{n}}}=0$ – est souvent justifiée par l'axiome que les nombres réels sont archimédiens. Cette attitude basée sur la limite envers $\scriptstyle 0,999\ldots$ est souvent formulée en termes plus imagés, mais moins précis. Par exemple, le manuel de 1846, « Arithmétique à l'université »«  » explique « $\scriptstyle 0,999+$, continué à l'infini est égal à 1, parce que l'addition de chaque nouveau 9 rapproche la valeur de 1. » ; l'« Arithmétique pour les écoles » de 1895 dit : « ... quand on prend un grand nombre de 9, la différence entre 1 et $\scriptstyle 0,9999\ldots$ devient petite de façon inconcevable. ». De telles approches heuristiques sont souvent interprétées par les étudiants comme une implication que $\scriptstyle 0,999\ldots$ est en soi quelque chose de différent de 1.

Segments emboîtés et bornes supérieures minimales

Segments emboîtés : en base 3, $\scriptstyle 1\,=\,1,000\ldots \,=\,0,222\ldots$

La définition par une série donnée ci-dessus est une façon simple de définir le nombre réel désigné par un développement décimal. Une approche complémentaire est conçue pour aborder le processus inverse : comment trouver le ou les développements décimaux pour le représenter.

Si on sait qu'un nombre réel $\scriptstyle x$ est dans l'intervalle fermé (ou segment) $\scriptstyle [0,10]$ (c'est-à-dire supérieur ou égal à 0 et inférieur ou égal à 10), on peut diviser cet intervalle en 10 parties égales, qui ne se recouvrent qu'à leurs extrémités : $\scriptstyle [0\,,\,1];[1\,,\,2];[2\,,\,3]$, etc, jusqu'à $\scriptstyle [9\,,\,10]$. Le nombre $\scriptstyle x$ doit appartenir à l'un de ces intervalles ; s'il appartient à $\scriptstyle [2,3]$, on note le chiffre « 2 », et on sous-divise l'intervalle en dix : $\scriptstyle [2,0\,,\,2,1];[2,1\,,\,2,2];[2,2\,,\,2,3]$, etc, jusqu'à $\scriptstyle [2,9\,,\,3]$. On note alors le séparateur décimal et le chiffre correspondant à l'intervalle où se trouve $\scriptstyle x$ ; en continant ce processus, on obtient une suite infinie de segments emboîtés, que l'on repère par une suite infinie de chiffres $\scriptstyle b_{0},b_{1},b_{2},b_{3},b_{4},\ldots$ et on écrit $\scriptstyle x=b_{0},b_{1}b_{2}b_{3}\ldots$

Dans ce formalisme, les identités $\scriptstyle 0,999\ldots \,=\,1$ et $\scriptstyle 1,000\ldots \,=\,1$ reflètent respectivement que 1 est à la fois dans le segment $\scriptstyle [0,1]$ et $\scriptstyle [1,2]$, si bien que l'on peut choisir l'un ou l'autre de ces intervalles pour commencer la recherche des décimales. La suite découle de ce choix initial. Pour s'assurer que cette notation n'abuse pas du signe « = », il faut trouver une manière de reconstruire un nombre réel unique pour ces représentations. Ceci peut se faire avec des limites, mais d'autres constructions utilisent les propriétés d'ordre

Un choix simple est celui du théorème des segments emboîtés (voir troisième solution), qui dit que dans une suite de segments emboîtés dont les longueurs deviennent arbitrairement petites, chaque intervalle contient exactement un point de l'intersection. Donc $\scriptstyle b_{0},b_{1}b_{2}b_{3}\ldots$ est défini comme le nombre unique appartenant à l'intersection de tous les segments

$\scriptstyle [b_{0}\,,\,b_{0}+1],~[b_{0},b_{1}\,,\,b_{0},b_{1}+0,1],~[b_{0},b_{1}b_{2}\,,\,b_{0},b_{1}b_{2}+0,01],~[b_{0},b_{1}b_{2}b_{3}\,,\,b_{0},b_{1}b_{2}b_{3}+0,001],~\ldots$

$\scriptstyle 0,999\ldots$ est donc le nombre réel unique qui se trouve dans tous les segments

$\scriptstyle [0\,,\,1],~[0,9\,,\,1],~[0,99\,,\,1],~[0,999\,,\,1],~\ldots$

c'est-à-dire 1.

Le théorème des segments emboîtés est d'habitude basé sur un caractère plus fondamental des nombres réels : l'existence de plus petites bornes supérieures ou suprema. Pour exploiter directement ce genre d'objet, on peut définir $\scriptstyle b_{0},b_{1}b_{2}b_{3}\ldots$ comme le supremum de l'ensemble des approximants $\scriptstyle b_{0},~b_{0},b_{1}~b_{0},b_{1}b_{2}~b_{0},b_{1}b_{2}b_{3}~\ldots$. On peut montrer ensuite que cette définition par les segments emboîtés est cohérente avec la procédure de subdivision, ce qui implique à nouveau que $\scriptstyle 0,999\ldots \,=\,1$. Tom Apostol conclut :

« Le fait qu'un nombre réel puisse avoir deux représentations décimales différentes est simplement un reflet de ce que deux ensembles différents de nombres réels peuvent avoir le même supremum.  »

Démonstrations à partir de la construction des nombres réels

Certaines approches définissent explicitement les nombres réels comme certaines structures basées sur les nombres rationnels, en utilisant la théorie axiomatique des ensembles. Les nombres naturels : 0, 1, 2, etc. commencent par 0 et continuent en croissant, si bien que chaque nombre a un successeur. On peut étendre les nombres naturels par les entiers négatifs, pour obtenir tous les entiers, puis à leurs rapports, ce qui donne les nombres rationnels. Ces systèmes de nombres sont accompagnés par l'arithmétique des quatre opérations (addition, soustraction, multiplication et division). De façon plus subtile, ils incluent la notion d'ordre, si bien qu'un nombre peut être comparé à un autre, et trouvé supérieur, inférieur ou égal à ce dernier.

Le passage des rationnels aux réels est une extension majeure. Il existe au moins deux manières courantes d'aboutir à ce résultat, toutes deux publiées en 1872 : les coupures de Dedekind et les suites de Cauchy. Les démonstrations que $\scriptstyle 0,999\ldots \,=\,1$ qui utilisent directement ces constructions ne se trouvent pas dans les manuels d'analyse réelle, où la tendance dans les dernières décennies a été d'utiliser l'analyse axiomatique. Même si une construction est proposée, elle est généralement utilisée à démontrer les axiomes des nombres réels, qui à leur tour permettent les démonstrations données ci-dessus. Cependant, certains auteurs expriment l'idée qu'il serait logiquement préférable de commencer par une construction, et que les démonstrations qui en découlent seront plus autonomes.

Les coupures de Dedekind

Dans l'approche des coupures de Dedekind, tout nombre réel $\scriptstyle x$ est défini comme l'ensemble infini de tous les rationnels inférieurs à $\scriptstyle x$. En particulier le nombre réel 1 est l'ensemble de tous les nombres rationnels inférieurs à 1. Tout développement décimal positif définit facilement une coupure de Dedekind : l'ensemble des rationnels inférieurs à une certaine extension du développement. Donc le nombre réel $\scriptstyle 0,999\ldots$ est l'ensemble des rationnels inférieurs à un des rationnels $\scriptstyle r$ qui peut prendre les valeurs $\scriptstyle 0,\,0,9,\,0,99$ ou tout autre nombre $\scriptstyle r\,=\,1-1/10^{n}$. Tous ces nombres sont inférieurs à 1, donc ils sont éléments du nombre réel 1. Inversement, un élément de 1 est un nombre rationnel $\scriptstyle a/b\,<\,1$, ce qui implique $\scriptstyle a/b\,<\,1-1/10^{b}$. Comme $\scriptstyle 0,999\ldots$ et $\scriptstyle 1$ contiennent les mêmes rationnels, ils définissent des ensembles identiques, et par définition $\scriptstyle 0,999\ldots \,=\,1$.

La définition des nombres réels comme coupures de Dedekind a été publiée pour la première fois par Richard Dedekind en 1872. La démarche ci-dessus pour faire correspondre un nombre réel à tout développement décimal est due à un papier d'éclaircissements intitulé « $\scriptstyle 0,999\ldots$ est-il égal à $\scriptstyle 1$ ? » par Fred Richman dans Mathematics Magazine, qui est destiné aux enseignants en premier cycle de l'université, et à leurs étudiants. Richman note que le fait de prendre des coupures de Dedekind sur n'importe ensemble dense des rationnels donne les mêmes résultats ; en particulier, il utilise les fractions décimales, pour lesquelles la démonstration est plus immédiate. Il note également que les démonstrations permettent de définir une coupure comme $\scriptstyle \{x\,:\,x\,<\,1\}$, mais pas $\scriptstyle \{x\,:\,x\,\leq \,1\}$ (ou vice-versa) « Pourquoi cela ? Précisément pour éliminer la possibilité de l'existence de nombres distincts 0,9* et 1. [...] Donc nous voyons que dans la définition traditionnelle des nombres réels, l'équation 0,9* = 1 est incorporée dès le début ». Une modification supplémentaire de la procédure conduit à une structure où les deux ne sont pas égaux. Bien qu'elle soit cohérente, beaucoup des règles de l'arithmétique usuelle n'y sont plus valables : par exemple, la fraction 1/3 n'a plus de représentation, (voir infra).

Suites de Cauchy

Une autre démarche pour construire les nombres réels utilise moins directement la notion d'ordre des rationnels. On commence par définir la distance entre $\scriptstyle x$ et $\scriptstyle y$ comme la valeur absolue $\scriptstyle |x-y|$, étant entendu que la valeur absolue $\scriptstyle |\,z\,|$ est la plus élevée des valeurs $\scriptstyle z$ et $\scriptstyle -z$, et par suite n'est jamais négative.

Dans ce cadre, les réels sont définis comme des suites de rationnels ayant la propriété des suites de Cauchy avec cette distance : Pour la suite $\scriptstyle (x_{0},\,x_{1}\,x_{2}\,\ldots )$, application des nombres naturels sur les rationnels, pour tout rationnel $\scriptstyle \delta$, il existe une valeur $\scriptstyle N$ telle que $\scriptstyle |x_{m}\,-\,x_{n}|\,<\,\delta$ pour tout $\scriptstyle m\,$ et $\scriptstyle n$ supérieurs à $\scriptstyle N$. En d'autres termes, la distance entre deux termes devient plus petite que n'importe quel rationnel positif à partir d'un certain rang.

Si $\scriptstyle x_{n}$ et $\scriptstyle y_{n}$ sont deux suites de Cauchy, elles sont dites égales au sens des nombres réels si la suite $\scriptstyle x_{n}\,-\,y_{n}$ admet comme limite $\scriptstyle 0$. Les troncations du nombre décimal $\scriptstyle b_{0},b_{1}b_{2}b_{3}\ldots$ forment une suite de rationnels qui est une suite de Cauchy. Elle est prise comme la valeur du nombre. Donc, dans ce formalisme, le travail se résume à montrer que la suite des rationnels :

$\scriptstyle 1\,-\,0~1\,-\,0,9~1\,-\,0,99~1\,-\,0,999,~\ldots =1~0,1~0,01~0,001~\ldots$

admet 0 pour limite, ou en d'autres termes que :

$\scriptstyle \lim _{n\to \infty }\,1/10^{n}\,=\,0$

C'est facile. Une démonstration possible est que pour $\scriptstyle \delta \,=a/b\,>\,0$, il suffit de prendre $\scriptstyle N\,=\,b$ dans la définition de la limite. Donc, à nouveau, $\scriptstyle 0,999\ldots \,=\,1$.

La définition des nombres réels comme suites de Cauchy a été publiée en premier séparément par Eduard Heine et Georg Cantor, également en 1872. La démarche précédente envers les développements décimaux, y compris le fait que $\scriptstyle 0,999\ldots \,=\,1$, suit de près le travail de Griffiths & Hilton de 1970 : « Manuel général de mathématique classique : une interprétation contemporaine ». Ce livre est écrit spécialement pour permettre un deuxième regard sur des concepts familiers, à la lumière des travaux contemporains.

Généralisations

Le résultat que $\scriptstyle 0,999\ldots \,=\,1$ se généralise facilement dans deux directions. Premièrement, tout nombre non-nul avec une notation décimale finie (ce qui signifie qu'il a ensuite indéfiniment des zéros), a une autre notation avec infiniment de 9 à la fin. Par exemple, $\scriptstyle 0,24999\ldots \,=\,0,25\ (=\,0,25000\ldots )$, exactement comme dans le cas que nous avons considéré. Ces nombres sont exactement les « fractions décimales », et elles forment un ensemble dense.

Deuxièmement, un théorème comparable s'applique dans toutes les bases. Par exemple, en base 2, (le système binaire), $\scriptstyle 0,111\ldots \,=\,1$, en base 3, $\scriptstyle 0,222\ldots \,=\,1$. Les manuels d'analyse réelle ont tendance à sauter le système décimal et à présenter l'une ou l'autre de ces généralisation pour commencer.

D'autres représentations de 1 existent aussi dans des bases non-entières. Par exemple, dans la base d'or, celle qui admet le nombre d'or comme base, les deux représentations standard de l'unité sont $\scriptstyle 1,000\ldots$ et $\scriptstyle 0,101010\ldots$, et il y a encore une infinité de représentations, contenant des suites de $\scriptstyle 111$ adjacents. En général, pour presque tout $\scriptstyle q$ entre 1 et 2, il y a une infinité non-dénombrable de développements en base $\scriptstyle q$ de 1. Inversement, il y a aussi une multiplicité non-dénombrable de $\scriptstyle q$ (dont tous les entiers) pour lesquels il n'y a qu'un développement de 1 autre que le trivial, 1,000... Ce résultat a été obtenu en 1990 par Paul Erdős, Miklos Horváth et István Joó. En 1998, Vilmos Komornik et Paola Loreti ont déterminé la plus petite de ces bases, la constante de Komornik-Loreti $\scriptstyle q\,=\,1,787231650\ldots$. Dans cette base, $\scriptstyle 1\,=\,0,11010011001011010010110011010011\ldots$ ; les décimales sont données par la suite de Prouhet-Thue-Morse, qui ne se répète pas.

Une généralisation bien plus profonde concerne les systèmes de numération positionnels les plus généraux. Ils admettent aussi des représentations multiples, et dans un certain sens, avec de pires difficultés. Par exemple :

• Dans le système ternaire équilibré (en) $\scriptstyle 1/2\,=\,0,111\ldots \,=\,0,{\underline {111}}\ldots$
• Dans le système factoriel inversé (utilisant les bases 2, 3, 4, ... pour les positions après la virgule), on a :

$\scriptstyle 1=1,0000\ldots =0,1234\ldots$

Impossibilité d'une représentation unique

Le fait que tous ces divers systèmes de numérations souffrent de représentations multiples pour certains nombres réels peut être attribué à une différence fondamentale entre l'ensemble ordonné des nombres réels et les collections de suites infinies ordonnées en ordre lexicographique. En fait les deux propriétés suivantes rendent compte des difficultés :

1. Si un intervalle des nombres réels est partitionné en deux parties non-vides L et R telles que tout élément de L est (strictement) inférieur à tout élément de R, alors : soit L contient un élément maximum ; soit R contient un élément minimum ; mais pas les deux à la fois.
2. La collection de toutes les suites de symboles choisis dans n'importe quel « alphabet », ordonnées lexicographiquement peut être partitionnée en deux parties non-vides L et R, telles que tout élément de L est plus petit que tout élément de R, et ce, de manière que L possède un élément maximum et R un élément minimum. En effet, il suffit de prendre deux débuts de suite avec un nombre donné de symboles, identiques à part leurs derniers symboles, qui se suivent, soient p₁ et p₂. Puis il suffit de prendre pour L toutes les suites commençant au plus par p₁ et pour R toutes les suites commençant au moins par p₂. Alors L a un élément maximum : la suite commençant par p₁ et continuant avec toujours le symbole le plus grand possible, et R a un élément minimum : la suite commençant par p₂ et continuant avec le symbole le plus petit possible à toutes les positions.

La première propriété découle d'une propriété de base des réels : L a un supremum et R un infimum, et ils sont égaux, sinon, il y aurait un intervalle entre les deux, et L,R ne serait pas une partition. Ce réel ne peut pas appartenir à la fois à L et à R, qui sont par hypothèse disjoints.

On aura reconnu comment le deuxième point généralise la situation obtenue avec 0,999... et 1,000... Nous n'avons fait nulle part l'hypothèse que le nombre de symboles admissibles soit le même à tous les éléments, ni même qu'ils soient indépendants les uns des autres. Dans ces conditions, la contradiction entre les propriétés énoncées montre qu'il ne peut pas y avoir de correspondance monotone et bijective entre une collection de suites de symboles et un intervalle des nombres réels : soit certains nombres ne correspondent à aucune suite, soit certains correspondent à plus d'une.

Marko Petkovšek a démontré que dans tout système positionnel susceptible de nommer tous les réels, l'ensemble des réels avec des représentations multiples est toujours dense. Il appelle la démonstration « un exercice instructif en topologie des ensembles de points » ; elle implique de considérer des ensembles de valeurs positionnelles, comme des espaces de Stone (en), et de remarquer que leurs représentations réelles sont données par des fonctions continues.

Applications

Une application de $\scriptstyle 0,999\ldots$ comme représentation de 1 se trouve dans la théorie des nombres élémentaire. En 1802, H. Goodwin a publié une observation sur l'apparition des 9 dans les développements décimaux périodiques de certaines fractions dont les dénominateurs sont certains nombres premiers. Par exemple :

• $\scriptstyle 1/7\,=\,0,142857142857\ldots$, et $\scriptstyle 142\,+\,857\,=\,428\,+\,571\,=\,285\,+\,714\,=\,999$.
• $\scriptstyle 1/73\,=\,0,0136986301369863\ldots$ et

$\scriptstyle 0136\,+\,9863\,=\,1369\,+\,8630\,=\,3698\,+\,6301\,=\,6986\,+\,3013\,=\,9999$.

E. Midy a démontré en 1836 un résultat général sur ce genre de fractions, maintenant connu sous le nom de théorème de Midy. La publication était obscure, et il n'est pas clair si sa démonstration impliquait directement $\scriptstyle 0,999\ldots$, mais au moins une démonstration moderne par W. G. Leavitt s'appuie sur cette représentation de $\scriptstyle 1$. Si l'on peut démontrer qu'un développement décimal de la forme $\scriptstyle 0,b_{1}b_{2}b_{3}\ldots$ est un nombre entier, alors ce doit être $\scriptstyle 1$. Ceci est la source du théorème. Les recherches dans ce sens peuvent motiver des recherches sur les PGCD, l'arithmétique modulaire, les premiers de Fermat, l'ordre des éléments de groupe et la réciprocité quadratique.

Positions de $\scriptstyle 1/4$ et de $\scriptstyle 2/3$ dans l'ensemble de Cantor

Pour retourner à l'analyse réelle, l'analogue en base $\scriptstyle 3$ : $\scriptstyle 0,222\ldots \,=\,1$ joue un rôle-clef dans la caractérisation de l'une des fractales les plus simples, l'ensemble de Cantor des tiers médians :

• un point dans l'intervalle unité $\scriptstyle [0,1]$ fait partie de l'ensemble de Cantor si et seulement si on peut le représenter en base $\scriptstyle 3$ en n'utilisant que les décimales $\scriptstyle 0$ et $\scriptstyle 2$. Ceci signifie que l'on va éliminer successivement tous les développements contenant un $\scriptstyle 1$, soit le tiers médian du dernier intervalle conservé.

La $\scriptstyle n$^e décimale de la représentation reflète la position à la $\scriptstyle n$^e étape de la construction. Par exemple, le point $\scriptstyle 2/3$ est donné par la représentation usuelle $\scriptstyle 0,2\,=\,0,2000\ldots$, car il est supérieur au tiers médian de $\scriptstyle [0,1]$, et inférieur au tiers médian de tous les intervalles conservés ultérieurement. Le plus intéressant ici est que $\scriptstyle 1/3$ appartient à l'ensemble de Cantor, parce que sa représentation comme $\scriptstyle 1/3=0,0222\ldots$ ne contient pas de $\scriptstyle 1$.

Les suites de $\scriptstyle 9$ apparaissent encore dans un autre des travaux de Cantor. Il faut les prendre en compte pour construire une démonstration valable de ce que l'intervalle réel unité est non-dénombrable, en utilisant son argument de la diagonale, de 1891. Ce genre de démonstration doit pouvoir déclarer que deux réels sont différents, sur la base de leurs développements décimaux, et il faut donc éviter des doublets comme $\scriptstyle 0,2$ et $\scriptstyle 0,1999\ldots \$. Une simple méthode représente tous les nombres avec des développements infinis ; une autre exclut les suites infinies de $\scriptstyle 9$. Une variante qui peut se rapprocher de l'argument original de Cantor utilise en fait la base 2, et par la conversion du développement en base 3 en base 2, on peut aussi démontrer la non-dénombrabilité de l'ensemble de Cantor.

Scepticisme dans l'enseignement

Les étudiants en mathématiques rejettent souvent l'égalité de $\scriptstyle 0,999\ldots$ et $\scriptstyle 1$, pour des raisons allant de leur apparence différente à des doutes profonds concernants le concept de limite et aux désaccords sur la nature des infinitésimaux. Il y a beaucoup de facteurs qui contribuent en commun à cette confusion :

• Les étudiants sont souvent « mentalement attachés à la notion qu'un nombre peut être représenté d'une seule manière par un développement décimal ». La vue de deux développements décimaux manifestement différents du même nombre apparaît comme un paradoxe, qui est amplifié par l'apparition du nombre apparemment bien connu : $\scriptstyle 1$.
• Certains étudiants interprètent $\scriptstyle 0,999\ldots$, ou toute notation semblable, comme une suite de $\scriptstyle 9$, longue certes, mais finie, de longueur variable, non spécifiée. Dans la mesure où ils acceptent une suite infinie, ils s'attendent néanmoins à ce que le dernier chiffre « à l'infini » soit un $\scriptstyle 9$.
• L'intuition et un enseignement ambigu conduisent les étudiants à penser la limite d'une suite comme un processus, plutôt qu'une valeur fixe, puisqu'une suite n'a pas besoin d'atteindre sa limite. Quand les étudiants acceptent la différence entre une suite de nombre et sa limite, ils peuvent lire $\scriptstyle 0,999\ldots$ comme la suite elle-même, plutôt que sa limite.

Ces idées sont erronées dans le contexte de la théorie standard des nombres réels, bien que certaines puissent être valables dans d'autres systèmes numériques, soit inventés pour leur utilité générale en mathématiques, soit comme des contre-exemples pour une meilleure compréhension de la nature de $\scriptstyle 0,999\ldots$.

Beaucoup de ces explications ont été trouvées par David O. Tall (en), qui a étudié les caractéristiques de l'enseignement et de la connaissance, qui conduisent à certaines des incompréhensions qu'il a rencontrées chez ses étudiants d'université. En interrogeant ses étudiants pour déterminer pourquoi une vaste majorité commençait par rejeter l'égalité, il a trouvé que « les étudiants continuent à concevoir $\scriptstyle 0,999\ldots$ comme une suite de nombres qui se rapproche toujours plus de $\scriptstyle 1$, mais pas comme une valeur fixée, au motif qu'on n'a pas spécifié combien il y a de décimales, ou que c'est le nombre décimal le plus proche en-dessous de $\scriptstyle 1$. ».

Parmi les démonstrations élémentaires, la multiplication de $\scriptstyle 0,333\ldots \,=\,1/3$ par $\scriptstyle 3$ est apparemment une bonne stratégie pour convaincre les étudiants réticents que $\scriptstyle 0,999\ldots \,=\,1$. Cependant, quand on leur fait comparer leur approbation de la première équation avec leurs doutes sur la deuxième, certains étudiants commencent à douter de la première, d'autres s'énervent. Les méthodes plus sophistiquées ne sont pas plus garanties : des étudiants qui sont tout à fait capables d'appliquer des définitions rigoureuses peuvent retomber sur le langage intuitif quand ils sont surpris par un résultat de mathématique tel que $\scriptstyle 0,999\ldots \,=\,1$. Par exemple, un étudiant en analyse réelle était capable de montrer que $\scriptstyle 0,333\ldots \,=\,1/3$ en utilisant la définition du supremum, mais insistaient sur le fait que $\scriptstyle 0,999\ldots \,<\,1$, sur la base de leur compréhension initiale de la division indéfinie. D'autres encore peuvent démontrer que $\scriptstyle 0,333\ldots \,=\,1/3$, mais, face à la démonstration par les fractions, insistent sur le fait que la « logique » prend le pas sur les calculs.

Joseph Mazur (en) raconte l'histoire d'un de ses étudiants en analyse numérique, brillant au reste, qui « mettait en doute à peu près tout ce que je disais en cours, mais ne doutait jamais de sa calculette, » et qui avait fini par croire que $\scriptstyle 9$ chiffres étaient tout ce dont on a besoin pour faire des mathématiques, y compris calculer la racine carrée de $\scriptstyle 23$. Cet étudiant continuait à douter de la valeur de l'argument de la limite $\scriptstyle 9,999\ldots \,=\,10$, l'appelant un « processus infiniment croissant sauvagement imaginé ».

Selon la théorie APOS de l'apprentissage mathématique, Dubinsky et al. proposent que les étudiants qui perçoivent $\scriptstyle 0,999\ldots$ comme une suite finie, indéterminée, dont la distance infiniment petite avec $\scriptstyle 1$, « n'ont pas fini de construire un concept du développement décimal infini ». D'autres étudiants qui ont fini de construire ce concept, ne sont sans doute pas capables d'encapsuler ce concept dans un concept d'objet, comme celui qu'ils ont pour $\scriptstyle 1$, et ils voient donc ces deux concepts comme incompatibles. Dubinsky et al. relient aussi cette capacité mentale d'encapsulation au fait de considérer une fraction comme $\scriptstyle 1/3$ comme un nombre véritable, et ainsi de travailler avec les ensembles de nombres.

Dans la culture populaire

Avec la croissance d'Internet, les débats sur $\scriptstyle 0,999\ldots$ sont sortis de la salle de classe, et se trouvent fréquemment dans les forums de discussion ou d'annonces, y compris beaucoup qui n'ont en principe que peu à voir avec les mathématiques.

• Dans le forum sci.math, la discussion sur $\scriptstyle 0,999\ldots$ est devenue un « sport de masse », et c'est une des questions abordées dans ses FAQ. La FAQ passe rapidement sur $\scriptstyle 1/3$, la multiplication par 10, les limites, et fait même allusion aux suites de Cauchy.

• Une édition de 2003 de la chronique générale The Straight Dope du Chicago Reader discute $\scriptstyle 0,999\ldots$ au moyen de $\scriptstyle 1/3$, et des limites, et parle des malentendus intérieurs en ces termes :

« Le primate inférieur qui est en nous résiste encore, disant $\scriptstyle 0,999\ldots$ ne représente pas vraiment un nombre, mais à la rigueur un processus. Pour trouver un nombre, il faut arrêter le processus, mais alors l'histoire de $\scriptstyle 0,999\ldots \,=\,1$ s'effondre.

N'importe quoi... »

• Cette même chronique The Straight Dope cite une discussion sur son propre forum de discussion, qui est sortie d'un autre forum non identifié « tournant autour des jeux vidéo ».

• Dans le même esprit la question de $\scriptstyle 0,999\ldots$ s'est trouvée un tel succès pendant les sept premières années du forum Battle.net de la société Blizzard Entertainment que la compagnie a émis un communiqué de presse le 1^er avril 2004, pour affirmer définitivement que c'est $\scriptstyle 1$ :

« Nous sommes très excités de fermer ce livre une fois pour toutes. Nous avons été témoins des peines de cœur et des soucis pour savoir si, oui ou non, $\scriptstyle 0,999\ldots \,=\,1$, et nous sommes fiers d'annoncer que la démonstration suivante résout finalement et de façon conclusive pour nos clients. »

Deux démonstrations sont alors proposées, basées sur les limites et sur la multiplication par 10.

• Pour donner une idée de la vivacité des discussions qui ont lieu sur la question, on peut dénombrer plus de 5000 interventions (entre 2005 et 2010) sur la page de discussion de l'article en:0.999... d'où le présent article est en majeure partie traduit, en y comprenant évidemment toutes les archives.

• $\scriptstyle 0,999\ldots$ fait aussi partie du folklore mathématique, et tout spécialement dans la plaisanterie suivante (Renteln et Dundes 2005, p. 27) :

« Question : Combien faut-il de mathématiciens pour visser une ampoule électrique ?
Réponse : $\scriptstyle 0,999999\ldots$ »

Dans les systèmes de numération alternatifs

Bien que les nombres réels forment un système de numération extrêmement utile, la décision d'interpréter la notation $\scriptstyle 0,999\ldots$ comme la représentation d'un nombre réel, finalement, n'est qu'une convention, et Timothy Gowers argumente, dans « Mathématiques : une introduction très brève » que l'identité qui en résulte $\scriptstyle 0,999\ldots \,=\,1$ est une convention aussi :

« On peut définir d'autres systèmes de numération utilisant de nouvelles règles, ou de nouveaux objets ; dans ce genre de systèmes, les preuves ci-dessus devraient être réinterprétées, et on pourrait bien trouver que dans tel ou tel système $\scriptstyle 0,999\ldots$ et $1$ ne soient pas identiques. Cependant, beaucoup de systèmes sont des extensions – ou des alternatives – par rapport au système des nombres réels, et $\scriptstyle 0,999\ldots \,=\,1$ continue à être vrai. Mais même dans ce genre de système, cela vaut la peine d'examiner le comportement de $\scriptstyle 0,999\ldots$ (dans la mesure où cette représentation a un sens, et en plus unique), mais aussi pour le comportement de phénomènes reliés. Si ces phénomènes diffèrent de ceux du système des nombres réels, alors au moins une des hypothèses de base de ce système est fausse.  »

Nombres infinitésimaux

Certaines démonstrations que $\scriptstyle 0,999\ldots \,=\,1$ reposent sur la propriété archimédienne des nombres réels standards : il n'y a pas d'infinitésimaux non-nuls. Il existe des structures algébriques mathématiquement cohérentes, comprenant diverses alternatives aux réels standards, qui ne sont pas archimédiennes. La signification de $\scriptstyle 0,999\ldots$ dépend de la structure dans laquelle on l'utilise. Par exemple les nombres duaux possèdent un nouvel élément, infinitésimal, $\scriptstyle \varepsilon$, analogue dans les nombres complexes à l'unité imaginaire $\scriptstyle i$, sauf que dans le cas des nombres duaux, $\scriptstyle \varepsilon ^{2}\,=\,0\,.$ La structure qui en résulte peut servir en dérivation algorithmique. Les nombres duaux peuvent être ordonnés par un ordre lexicographique, auquel cas les multiples de $\scriptstyle \varepsilon$ deviennent des éléments non-archimédiens. Noter, cependant que, considérés comme une extension des réels, les duaux satisfont encore $\scriptstyle 0,999\ldots \,=\,1$. Notre encore que puisque $\scriptstyle \varepsilon$ existe en tant que nombre dual, $\scriptstyle \varepsilon /2$ existe aussi, si bien que $\scriptstyle \varepsilon$ n'est pas « le plus petit nombre dual positif », et d'ailleurs, comme pour les réels, ce nombre n'existe pas.

L'analyse non-standard fournit un système de numération avec tout un ensemble d'infinitésimaux (et leurs inverses, infiniment grands). A. H. Lightstone a mis au point un développement décimal pour les nombres hyperréels dans l'intervalle $\scriptstyle (0\,,\,1)^{\ast }$. Il montre comment associer à tout nombre une suite de décimales $\scriptstyle 0,d_{1}d_{2}d_{3}\ldots ;\ldots d_{\infty -1}d_{\infty }d_{\infty +1}\ldots$ indexée par les nombres hypernaturels. Bien qu'il ne discute pas directement $\scriptstyle 0,999\ldots$, il montre que le nombre réel $\scriptstyle 1/3$ est représenté par $\scriptstyle 0,333\ldots ;\ldots 333\ldots$, ce qui est une conséquence de l'axiome de transfert. En multipliant par $\scriptstyle 3$, on obtient une représentation analogue pour des développements avec des $\scriptstyle 9$ qui se répètent. Mais Lightstone montre que dans ce système, les expressions $\scriptstyle 0,333\ldots ;\ldots 000\ldots$ – ou $\scriptstyle 0,999\ldots ;\ldots 000\ldots$ – ne correspondent à aucun nombre.

En même temps, le nombre hyperréel $\scriptstyle u_{H}\,=\,0,999\ldots ;\ldots 999000\ldots$ avec la dernière décimale $\scriptstyle 9$ à un rang hypernaturel infini $\scriptstyle H$ satisfait à l'inégalité stricte $\scriptstyle u_{H}<1$. En fait, la suite : $\scriptstyle u_{1}=0,9\,;\ u_{2}=0,99\,;\ u_{3}=0,9999\,;~$et $\scriptstyle u_{H}\,=\,1-10^{-H}\,<\,1\,.$ Selon cette écriture, Karin Katz et Mikhail Katz ont proposé une évaluation différente de $\scriptstyle 0,999\ldots$ :

${\begin{array}{cl}\scriptstyle 0,\underbrace {\scriptstyle 999\ldots } &\scriptstyle =\,1-1/10^{[\mathbb {N} ]}\\[-1ex]\scriptstyle [\mathbb {N} ]&\end{array}}$

où $\scriptstyle [\mathbb {N} ]$ est un hypernaturel infini donné par la suite $\scriptstyle 1,\,2,\,3,\,\ldots$, modulo un certain ultrafiltre. Ian Stewart caractérise cette interprétation comme une façon « tout à fait raisonnable » de justifier rigoureusement l'intuition qu'il « manque un petit quelque chose entre $\scriptstyle 0,999\ldots$ et $\scriptstyle 1$ ». Avec Katz et Katz, Robert Ely met en question la supposition que les idées des étudiants sur le fait que $\scriptstyle 0,999\ldots \,<\,1$ sont des idées fausses sur les nombres réels, et il préfère les interpréter comme des intuitions non-standard, qui pourraient être valable dans l'étude de l'analyse.

Hackenbush

La théorie des jeux combinatoires fournit également des nombres alternatifs aux réels, avec le jeu HackenbushHackenbush L-R infini comme exemple particulièrement frappant. En 1974, Elwyn BerlekampElwyn Berlekamp décrit une correspondance entre les chaînes du jeu Hackenbush et les développements binaires des réels, motivé par l'idée de la compression de données. Par exemple, la valeur de la chaîne Hackenbush LRRLRLRL... est $\scriptstyle 0,010101\ldots _{\mathrm {(base2)} }\,=\,1/3$. Cependant la valeur de LRLLL... (correspondant à $\scriptstyle 0,111\ldots _{\mathrm {(base\ 2)} }$ est infinitésimalement inférieur à $\scriptstyle 1$. La différence entre les deux est le nombre surréel $\scriptstyle 1/\omega$, où $\scriptstyle \omega$ est le premier ordinal infini ; la représentation correspondante est LRRRR..., ou $\scriptstyle 0,000\ldots _{\mathrm {(base\ 2)} }$.

Brisure de la soustraction

Une autre manière par laquelle les démonstrations peuvent être rendues invalides est le cas où $\scriptstyle 1-0,999\ldots$ n'existe tout simplement pas, parce que la soustraction n'est pas toujours possible. Les structures mathématiques où il existe une opération d'addition, mais où l'opération de soustraction n'est pas toujours définie comprennent les semi-groupes commutatifs, les monoïdes commutatifs et les semi-anneaux. Richman considère un tel système, construit de façon que $\scriptstyle 0,999\ldots \,<\,1\,.$

Tout d'abord, Richman définit un « nombre décimal » comme une expression décimale littérale. Il définit l'ordre lexicographique, et une opération d'addition, notant que $\scriptstyle 0,999\ldots \,<\,1\,,$ tout simplement parce que $\scriptstyle 0\,=\,1$ au rang des unités, mais pour tout $\scriptstyle x$ dont le développement ne se termine pas, on a $\scriptstyle 0,999\ldots \,+\,x=\,1\,+\,x\,.$ Donc une particularité des nombres décimaux est que l'addition ne peut pas toujours être compensée : une autre est qu'il n'y a pas de nombre décimal correspondant à $\scriptstyle 1/3$. Après avoir défini la multiplication, les nombres décimaux forment un semi-anneau positif, totalement ordonné et commutatif.

Dans le processus de définition de la multiplication, Richman définit aussi un autre système qu'il appelle « coupures D », voisin de l'ensemble des coupures de Dedekind sur les fractions décimales. Normalement cette définition conduit aux nombres réels, mais il la change légèrement pour les fractions décimales $\scriptstyle d$ en permettant à la fois la coupure $\scriptstyle (-\infty \,,\,d)$ et la coupure $\scriptstyle (-\infty \,,\,d]$, nommée « coupure principale ». Il n'y a pas d'infinitésimaux positifs dans les coupures D, mais il y a une sorte d'« infinitésimal négatif » $\scriptstyle 0^{-}$, qui n'a pas de développement décimal. Il conclut que $\scriptstyle 0,999\ldots \,=\,1\,+\,0^{-}\,,$ tandis que l'équation $\scriptstyle 0,999\ldots \,+\,x\,=,1$ n'a pas de solution.

Nombres p-adiques

Quand on leur pose des questions sur $\scriptstyle 0,999\ldots \,,$ les novices croient souvent qu'il doit y avoir un « dernier $\scriptstyle 9$ », ce qui fait qu'ils pensent que $\scriptstyle 1\,-\,0,999\ldots$ est un nombre positif, qu'ils écrivent $\scriptstyle 0,000\ldots 1\,.$ Que cela ait ou non un sens, le but intuitif est clair : si l'on ajoute un $\scriptstyle 1$ au dernier des $\scriptstyle 9\,,$ cela va provoquer des retenues en cascade, remplacer tous les $\scriptstyle 9$ par des $\scriptstyle 0\,,$ et le $\scriptstyle 0$ des unités en un $\scriptstyle 1\,.$ Parmi d'autres raisons, cette idée échoue, parce qu'il n'y a pas de « dernier $\scriptstyle 9$ » dans $\scriptstyle 0,999\ldots$. Cependant il existe un système qui contient une infinité de $\scriptstyle 9\,,$ y compris un dernier $\scriptstyle 9\,.$

Les entiers 4-adiques (points noirs), comprenant la suite $\scriptstyle (3,\ 33\ 333\ \ldots )$ convergeant vers $\scriptstyle -1$. L'analogue 10-adique est $\scriptstyle \ldots 999=-1$.

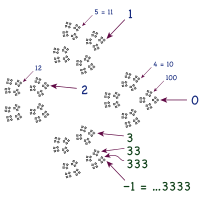
Les nombres p-adiques sont un système de numération alternatif de grand intérêt en théorie des nombres. Comme les nombres réels, les nombres p-adiques peuvent être construits à partir des rationnels, au moyen de suites de Cauchy ; la construction utilise une métrique différente, dans laquelle $\scriptstyle 0$ est plus proche de $\scriptstyle p\,,$ et encore plus de $\scriptstyle p^{n}$ que de 1. Les nombres p-adiques forment un corps si p est premier, et un anneau sinon, y compris $\scriptstyle p\,=\,10$. Donc on peut faire de l'arithmétique avec les nombres p-adiques, et il n'y a pas d'infinitésimaux.

Dans les nombres 10-adiques, les analogues des développements décimaux s'étendent vers la gauche. Le développement $\scriptstyle \ldots 999$ possède un dernier $\scriptstyle 9\,,$ tandis qu'il n'a pas de premier $\scriptstyle 9\,.$ On peut ajouter 1 au chiffre des unités, et les retenues en cascade ne laissent que des $\scriptstyle 0$ :

$\scriptstyle \ldots 999\,+\,1\,=\,\ldots 000\,=\,0$

donc $\scriptstyle \ldots 999\,=\,-1$. Une autre démonstration utilise une série géométrique. La série infinie impliquée par la notation $\scriptstyle \ldots 999$ ne converge pas dans les réels, mais elle converge dans les 10-adiques, et on peut réutiliser la formule familière :

$\scriptstyle \ldots 999=9+9(10)+9(10)^{2}+9(10)^{3}+\cdots ={\frac {9}{1-10}}=-1$.

– à comparer avec la série (voir supra).

Une troisième démonstration a été inventée par par un élève de cinquième, qui doutait de l'argument de la limite donné par son professeur, que $\scriptstyle 0,999\ldots \,=\,1$, mais était inspiré par la démonstration par la multiplication par 10 (voir supra), mais à l'envers : si $\scriptstyle x\,=\,\ldots 999$ alors $\scriptstyle 10x\,=\,\ldots 9990\,=\,x-9$, et par suite $\scriptstyle x\,=\,-1$.

Une extension finale, puisque $\scriptstyle 0,999\ldots \,=\,1$ dans les réels et $\scriptstyle \ldots 999\,=\,-1$ dans les 10-adiques, « par une foi aveugle et un jonglage inconsidéré avec les symboles », on peut ajouter les deux relations, et arriver à $\scriptstyle \ldots 999,999\ldots \,=\,0$. Cette équation n'a de sens ni comme développement 10-adique, ni comme développement décimal, mais il se trouve qu'on peut lui donner une signification si l'on développe une théorie des « doubles-décimales », avec des côtés gauches périodiques, pour représenter un système familier : celui des nombres réels.

Problèmes connexes

• Voir l'article Logique intuitionniste.

• Les paradoxes de Zénon, et en particulier celui d'Achille et de la tortue, sont voisins du paradoxe apparent que $\scriptstyle 0,999\ldots \,=\,1\,.$ Le paradoxe peut être modélisé mathématiquement, et comme $\scriptstyle 0,999\ldots \,,$ résolu par une série géométrique. Cependant, il n'est pas clair que ce traitement mathématique s'applique aux questions d'ordre métaphysique que Zénon explorait.

• La division par zéro intervient dans certaines des discussions populaires de $\scriptstyle 0,999\ldots \,,$ et excite également des controverses. Tandis que la plupart des auteurs choisissent de définir $\scriptstyle 0,999\ldots \,,$ presque tous les traitements modernes laissent indéfinie la division par zéro, parce qu'on ne peut pas lui assigner de signification dans le champ des nombres réels standards. Cependant, la division par zéro peut être définie dans certains autres systèmes, comme dans l'analyse complexe, où on peut ajouter un point à l'infini aux nombres finis pour obtenir la sphère de Riemann. Dans ce cas, cela a un sens de définir $\scriptstyle 1/0$ comme l'infini; et, en fait, les résultats sont profonds et applicable à de nombreux problèmes en ingénierie et physique. Certains mathématiciens éminents avaient plaidé pour ce genre de définition bien avant que l'un de ces systèmes de numération ne soit mis au point.

• Le zéro négatif est encore une structure redondante de bien des façons d'écrire les nombres. Dans des systèmes de numération tels que les réels, où $\scriptstyle 0$ dénote l'identité pour l'addition, il n'est ni positif ni négatif, et l'interprétation usuelle de $\scriptstyle -0$ est que c'est l'inverse de $\scriptstyle 0$ pour l'addition, ce qui force $\scriptstyle -0\,=\,0$. Néanmoins, certaines applications scientifiques utilisent des zéros positif et négatif distincts, comme le font la plupart des ordinateurs (par exemple, les entiers stockés sous la forme de signe et valeur absolue, ou complément à un, ou les nombre à virgule flottante, spécifiés par le standard IEEE pour les virgules flottantes.

Bibliographie

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « 0.999... » (voir la liste des auteurs).

Liens internes

Voir notamment :

* Développement décimal	* Décimale récurrente	* 1 (nombre)
* Série géométrique	* Série	* Infini
* Limite	* Nombre réel	* Analyse réelle
* Analyse non standard	* Mathématiques

Références externes

• (en)Cecil Adams, « An infinite question: Why doesn't .999~ = 1? », The Straight Dope, 11 juillet 2003 (consulté le 24 avril 2010)
• (en) Alligood, Sauer et Yorke, Chaos: An introduction to dynamical systems, Springer, 1996 (ISBN 0-387-94677-2), chap. 4.1 (« Cantor Sets »)
  Ce manuel d'introduction aux systèmes dynamiques est destiné aux étudiants du premier cycle et du début de deuxième cycle universitaire (p. ix)
• (en) Tom M. Apostol, Mathematical analysis, Addison-Wesley, 1974, 2^e éd. (ISBN 0-201-00288-4)
  Passage de l'analyse élémentaire à l'analyse avancée, Mathematical analysis a l'ambition d'être « honnête, rigoureux, à jour, et en même temps, pas trop pédant. » (préface). Les développements d'Apostol sur les nombres réels utilisent l'axiome de l'infimum et introduisent les développements décimaux deux pages plus loin (p. 9-11)
• (en) R.G. Bartle et D.R. Sherbert, Introduction to real analysis, Wiley, 1982 (ISBN 0-471-05944-7)
  Ce manuel vise à être « un manuel accessible, de rythme raisonnable, qui traite des concepts et techniques fondamentaux de l'analyse réelle ». Son développement sur les réels repose sur l'axiome du supremum (p. vii-viii)
• (en) Richard Beals, Analysis, Cambridge University Press, 2004 (ISBN 0-521-60047-2)
• (en) Elwyn R. Berlekamp, J.H. Conway et R.K. Guy, Winning Ways for your Mathematical Plays, Academic Press, 1982 (ISBN 0-12-091101-9)
• (en) Martin Berz, Computer Arithmetic and Enclosure Methods : Automatic differentiation as nonarchimedean analysis, Elsevier, 1992 (résumé), p. 439–450
• Blizzard, « Blizzard Entertainment Announces .999~ (Repeating) = 1 », Blizzard Entertainment, 1^er avril 2004 (consulté le 24 avril 2010)
• (en) Bonnycastle, An Introduction to Algebra, 1811
• (en) Bryan H. Bunch, Mathematical fallacies and paradoxes, Van Nostrand Reinhold, 1982 (ISBN 0-442-24905-5)
  Ce livre présente une analyse des paradoxes et faussetés, comme un outil pour explorer son sujet central « la relation assez ténue entre réalité mathématique et réalité physique ». Il suppose connue l'algèbre de seconde ; les mathématiques supplémentaires sont apportées par le livre, y compris les séries géométriques au chapitre 2. Bien que $\scriptscriptstyle 0,999\ldots$ ne soit pas l'un des paradoxes entièrement traités, il est brièvement mentionné au cours d'un développement sur la méthode de Cantor. (p. ix-xi, 119)
• (en) Brian Burrell, Merriam-Webster's Guide to Everyday Math: A Home and Business Reference, Merriam-Webster, 1998 (ISBN 0-87779-621-1)
• (en) William Byers, How Mathematicians Think : Using Ambiguity, Contradiction, and Paradox to Create Mathematics, Princeton Universiy Press, 2007 (ISBN 0-691-12738-7)
• (en) John B. Conway, Functions of one complex variable I, Springer, 1978, 2^e éd. (ISBN 0-387-90328-3)
  Ce texte suppose « un solide cours de calcul analytique » comme préalable ; ses buts avoués sont de présenter l'analyse complexe comme « une introduction aux mathématiques » et d'en expliciter les matières avec clarté et précision. (p. vii)
• (en) Charles Davies, The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications, A.S. Barnes, 1846 (lire en ligne)
• (en) Frank C. DeSua, « A system isomorphic to the reals », The American Mathematical Monthly, vol. 67, n^o 9,‎ novembre 1960, p. 900–903 (DOI 10.2307/2309468)
• (en) Ed Dubinsky, Kirk Weller, Michael McDonald et Anne Brown, « Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2 », Educational Studies in Mathematics, vol. 60,‎ 2005, p. 253–266 (DOI 10.1007/s10649-005-0473-0)
• (en) Barbara Edwards et Michael Ward, « Surprises from mathematics education research: Student (mis)use of mathematical definitions », The American Mathematical Monthly, vol. 111, n^o 5,‎ mai 2004, p. 411–425 (lire en ligne)
• (en) Herbert B. Enderton, Elements of set theory, Elsevier, 1977 (ISBN 0-12-238440-7)
  Un manuel de premier cycle universitaire en théorie des ensembles, qui ne « préjuge d'aucune formation ». Il est écrit pour accompagner un cours centré sur la théorie axiomatique des ensembles, ou sur la construction des systèmes numériques ; le matériel axiomatique est marqué afin de pouvoir être démystifié. (p. xi-xii)
• (en) Leonhard Euler (trad. John Hewlett, Francis Horner), Elements of Algebra : Traduction anglaise, Orme Longman, 1822, 3^e éd. (ISBN 0387960147, lire en ligne)
• (en) Paul Fjelstad, « The repeating integer paradox », The College Mathematics Journal, vol. 26, n^o 1,‎ janvier 1995, p. 11–15 (DOI 10.2307/2687285)
• (en) Anthony Gardiner, Understanding Infinity: The Mathematics of Infinite Processes, Dover, 2003 (ISBN 0-486-42538-X)
• (en) Timothy Gowers, Mathematics: A Very Short Introduction, Oxford University Press, 2002 (ISBN 0-19-285361-9)
• (en) Ivor Grattan-Guinness, The development of the foundations of mathematical analysis from Euler to Riemann, MIT Press, 1970 (ISBN 0-262-07034-0)
• (en) H.B. Griffiths et P.J. Hilton, A Comprehensive Textbook of Classical Mathematics : A Contemporary Interpretation, Londres, Van Nostrand Reinhold, 1970 (ISBN 0-442-02863-6)
  Ce livre est l'aboutissement d'un cours pour les professeurs de mathématiques du secondaire dans la région de Birmingham. Le cours était destiné à donner une perspective universitaire sur l'enseignement des mathématiques à l'école, et le livre vise les étudiants « qui ont en gros le niveau demandé après une année d'études spécialisées en mathématiques à l'université ». Les nombres réels sont construits au chapitre 24, « chapitre peut-être le plus difficile de tout le livre », bien que les auteurs attribuent une bonne partie de la difficulté à leur utilisation de la théorie des idéaux, qui n'est pas reproduite ici. (p. vii, xiv)
• (en) K. Katz et M. Katz, « When is .999… less than 1 ? », The Montana Mathematics Enthusiast, vol. 7, n^o 1,‎ 2010a, p. 3–30 (lire en ligne)
• (en)Karin Usadi Katz, Mikhail G. Katz, « Zooming in on infinitesimal 1 − .9.. in a post-triumvirate era », Educational Studies in Mathematics, Springer Verlag, 7 mars 2010 (DOI 10.1007/s10649-010-9239-4, consulté le 24 avril 2010)</ref>
• (en) A.J. Kempner, « Anormal Systems of Numeration », The American Mathematical Monthly, vol. 43, n^o 10,‎ décembre 1936, p. 610–617 (DOI 10.2307/2300532)
• (en) Vilmos Komornik et Paola Loreti, « Unique Developments in Non-Integer Bases », The American Mathematical Monthly, vol. 105, n^o 7,‎ 1998, p. 636–639 (DOI 10.2307/2589246)
• (en) Herbert Kroemer et Charles Kittel, Thermal Physics, W. H. Freeman, 1980, 2^e éd. (ISBN 0-7167-1088-9), p. 462
• (en) W.G. Leavitt, « A Theorem on Repeating Decimals », The American Mathematical Monthly, vol. 74, n^o 6,‎ 1967, p. 669–673 (DOI 10.2307/2314251)
• (en) W.G. Leavitt, « Repeating Decimals », The College Mathematics Journal, vol. 15, n^o 4,‎ septembre 1984, p. 299–308 (DOI 10.2307/2686394)
• (en)Joseph Lewittes, « Midy's Theorem for Periodic Decimals », New York Number Theory Workshop on Combinatorial and Additive Number Theory, arXiv, 2006 (consulté le 23 avril 2010)
• (en) A.H. Lightstone, « Infinitesimals », The American Mathematical Monthly, vol. 79, n^o 3,‎ mars 1972, p. 242–251 (DOI 10.2307/2316619)
• (en) Richard Mankiewicz, The story of mathematics, Londres, Cassell, 2000 (ISBN 0-304-35473-2)
  Mankiewicz cherche à présenter « l'histoire des mathématiques de façon accessible » en combinant les aspects visuels et qualitatifs des mathématiques, les écrits de mathématiciens, et des ébauches historiques (p.8).
• (en) Eli Maor, To infinity and beyond: a cultural history of the infinite, Birkhäuser, 1987 (ISBN 3-7643-3325-1)
  Revue de l'infini, par thèmes plutôt que chronologique, ce livre est « destiné au lecteur généraliste », mais « raconté du point de vue d'un mathématicien ». À propos du dilemme entre rigueur et lisibilité, Maor commente : « J'espère avoir convenablement résolu ce problème » (p. x-xiii).
• (en) Joseph Mazur, Euclid in the Rainforest: Discovering Universal Truths in Logic and Math, Pearson: Pi Press, 2005 (ISBN 0-13-147994-6)
• (en)MSDN, « Floating point types », 2010 (consulté le 24 avril 2010)
• (en) James R. Munkres, Topology, Prentice Hall, 2000, 2^e éd. (ISBN isbn=0-13-181629-2^{[à vérifier : ISBN invalide]})
  Pensé comme une introduction à la topologie, « au niveau du 2^e cycle universitaire », sans connaissances préalables : « je ne suppose même pas que le lecteur en connaisse beaucoup en théorie des ensembles » (p. xi). Le traitement des réels par Munkres est axiomatique ; il prétend construire à la main : « Cette manière d'approcher le sujet demande pas mal de temps et d'efforts, et cela a une valeur plus logique que mathématique. » (p.30)
• (en) Rafael Núñez, Do Real Numbers Really Move? Language, Thought, and Gesture: The Embodied Cognitive Foundations of Mathematics, vol. 18 : Unconventional Essays on the Nature of Mathematics, Springer, 2006 (ISBN 978-0-387-25717-4, lire en ligne), p. 160–181
• (en)J. J. O'Connor, E. F. Robertson, « History topic: The real numbers: Stevin to Hilbert », MacTutor History of Mathematics, octobre 2005 (consulté le 19 avril 2010)
• (en) George Pedrick, A First Course in Analysis, Springer, 1994 (ISBN 0-387-94108-8)
• (en) Anthony Peressini et Dominic Peressini, Perspectives on Mathematical Practices, vol. 5, Springer, 2007 (ISBN 978-1-4020-5033-6), « Philosophy of Mathematics and Mathematics Education »
• (en) Marko Petkovšek, « Ambiguous Numbers are Dense », American Mathematical Monthly, vol. 97, n^o 5,‎ mai 1990, p. 408–411 (DOI 10.2307/2324393)
• (en) Márcia Pinto et David Tall, Following students' development in a traditional university analysis course, PME25, 2001 (lire en ligne), v4: 57–64
• (en) M.H. Protter et Charles B. Morrey, A first course in real analysis, Springer, 1991, 2^e éd. (ISBN 0-387-97437-7)
  Ce livre vise à « présenter une fondation théorique de l'analyse convenable pour les étudiants qui ont terminé un cours standard sur le calcul analytique » (p. vii). À la fin du chapitre 2, les auteurs supposent comme axiome pour les réels que des suites bornées non-décroissantes convergent, démontrant plus tard le théorème des segments imbriqués et la propriété du supremum (p. 56–64). Les développements décimaux apparaissent dans l'appendice 3, « développements des réels dans une base quelconque » (p. 503–507)
• (en) Charles Chapman Pugh, Real mathematical analysis, Springer, 2001 (ISBN 0-387-95297-7)
  Supposant le lecteur familier avec les rationnels, Pugh introduit les coupures de Dedekind dès que possible, disant du traitement axiomatique : « Ceci est une sorte d'entourloupe, puisque toute l'analyse est fondée sur le système des réels. » (p. 10) Après avoir démontré la propriété du supremum et quelques faits connexes, les coupures ne sont plus utilisées pour le reste du livre.
• (en) Fred Richman, « Is 0.999… = 1? », Mathematics Magazine, vol. 72, n^o 5,‎ décembre 1999, p. 396–400 (lire en ligne)
  Le texte publié peut montrer quelques différences avec le preprint donné en lien.
• (en) Abraham Robinson, Non-standard analysis, Princeton University Press, 1996 (ISBN 0-691-04490-2)
• (en) Maxwell Rosenlicht, Introduction to Analysis, Dover, 1985 (ISBN 0-486-65038-3)
  Ce livre donne une introduction « prudente et rigoureuse » à l'analyse réelle. Il donne les axiomes des réels, puis les construit (p. 27-31) comme des développements décimaux infinis, avec 0.999…=1 comme partie de la définition.
• (en) Walter Rudin, Principles of mathematical analysis, McGraw-Hill, 1976, 3^e éd. (ISBN 0-07-054235-X)
  Manuel pour un cours de second cycle universitaire avancé. « L'expérience m'a convaincu qu'il est pédagogiquement malavisé (bien que correct logiquement) de démarrer la construction des réels à partir des rationnels. Au début, la plupart des étudiants ne voient tout simplement pas pourquoi le faire. Donc on introduit le système des réels comme un corps ordonné satisfaisant la condition du supremum, et on en montre rapidement quelques propriétés. Cependant la construction de Dedekind n'est pas omise. Elle est mise en appendice du chapitre 1, où elle peut être étudiée et admirée quand le temps en est venu. »(p. ix)
• (en) Maurice Shrader-Frechette, « Complementary Rational Numbers », Mathematics Magazine, vol. 51, n^o 2,‎ mars 1978, p. 90–98
• (en) Charles Smith et Charles Harrington, Arithmetic for Schools, Macmillan, 1895 (résumé)
• (en) Houshang Sohrab, Basic Real Analysis, Birkhäuser, 2003 (ISBN 0-8176-4211-0)
• (en) Ian Stewart, The Foundations of Mathematics, Oxford University Press, 1977 (ISBN 0-19-853165-6)
• (en) Ian Stewart, Professor Stewart's Hoard of Mathematical Treasures, Profile Books, 2009 (ISBN 978-1-84668-292-6)
• (en) Ian Stewart, Calculus: Early transcendentals, Brooks/Cole, 1999, 4^e éd. (ISBN 0-534-36298-2)
  Ce livre vise à « aider les étudiants à découvrir le calcul analytique » et à « se concentrer sur la compréhension des concepts » (p. v). Il omet les démonstrations des fondations du calcul analytique.
• (en) D. O. Tall et R.L.E. Schwarzenberger, « Conflicts in the Learning of Real Numbers and Limits », Mathematics Teaching, vol. 82,‎ 1978, p. 44–49 (lire en ligne)
• (en) David Tall, « Conflicts and Catastrophes in the Learning of Mathematics », Mathematical Education for Teaching, vol. 2, n^o 4,‎ 1976 (lire en ligne)
• (en) David Tall, « Cognitive Development In Advanced Mathematics Using Technology », Mathematics Education Research Journal, vol. 12, n^o 3,‎ 2000, p. 210–230 (lire en ligne)
• (de) Dr. Hans von Mangoldt, Einführung in die höhere Mathematik, Leipzig, Verlag von S. Hirzel, 1911, 1^re éd., « Chap. : Reihenzahlen »
• (en)Hans de Vreught, « sci.math FAQ: Why is 0.9999… = 1? » (consulté le 24 avril 2010)
• (en)A. N. Walker, « Hackenstrings and the 0.999… ?= 1 FAQ », 1999 (consulté le 24 avril 2010)</ref>
• (en) David Foster Wallace, Everything and more: a compact history of infinity, Norton, 2003 (ISBN 0-393-00338-8)

Lectures complémentaires

à remplir