Série géométrique

1/2 + 1/4 + 1/8 + 1/16 + ⋯ = 1
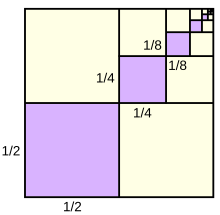
1/4 + 1/16 + 1/64 + 1/256 + ⋯ = 1/3 :
chacun des carrés violets mesure 1/4 de la surface du grand carré le plus proche (1/2×1/2 = 1/4, 1/4×1/4 = 1/16, etc.). Par ailleurs, la somme des aires des carrés violets est égale à un tiers de la superficie du grand carré.
En mathématiques, une série géométrique est une série définie par une suite géométrique, c'est-à-dire que le ratio de deux termes successifs de la série est constant. Par exemple la série numérique :
est une série géométrique de raison 1/2, parce que chaque terme est le produit du précédent par 1/2.
Le calcul explicite des sommes partielles d'un série géométrique permet d'étudier simplement sa convergence. On peut définir les séries géométrique de nombres réels, de nombres complexes et généraliser à n'importe quelle algèbre de Banach.
Définition dans le corps des réels[modifier | modifier le code]
Soit une suite géométrique à valeurs réelles de terme initial et de raison . La suite des sommes partielles de cette suite est définie par
Accessoirement, on peut en déduire l'élément suivant de la suite :
Terme général[modifier | modifier le code]
Sachant que le terme général de la suite géométrique (uk) est uk = aqk, et en excluant le cas q = 1 qui donne Sn = (n + 1)a, le terme général de la suite (Sn) des sommes partielles de la série s'écrit :
- .
De manière plus générale, pour une suite géométrique de raison q et dont on veut connaître la somme partielle entre les naturels i et j (i ≤ j), la formule est la suivante :
- .
Exemple numérique[modifier | modifier le code]
On cherche à calculer la somme des puissances k-ièmes de 2 pour k entier allant de 0 à 8. C'est la somme des 9 premiers termes de la suite géométrique de raison 2 et de premier terme 1 :
- .
La formule de la section précédente s'écrit ici :
- .
Preuve par récurrence[modifier | modifier le code]
L'identité est vraie pour n = 0. Supposons-la vérifiée au rang n. Alors,
- ,
ce qui montre l'assertion au rang n + 1.
Preuve directe[modifier | modifier le code]
Pour un entier naturel n fixé, on multiplie Sn par q, puis on soustrait le résultat obtenu à Sn[1] :
(c'est une somme télescopique). On obtient donc
- ,
c'est-à-dire :
- .
Preuve utilisant des règles de proportionnalité[modifier | modifier le code]
C'est la démarche employée par Euclide dans le Livre IX de ses Éléments, théorème 33 proposition XXXV, pour des nombres entiers positifs[2]. Il utilise une propriété qu'il a également démontrée : quand plusieurs fractions sont égales, elles sont aussi égales à la fraction obtenue en faisant la somme des numérateurs divisée par la somme des dénominateurs.
Or, dans une suite géométrique, il y a égalité des rapports entre deux termes consécutifs mais aussi égalité du rapport entre la différence de deux termes consécutifs et le premier d'entre eux. En langage mathématique, cela donne
puis, en sommant les numérateurs entre eux et les dénominateurs entre eux :
Une telle démonstration reste valable tant que les termes de la suite sont non nuls et la somme est non nulle.
Convergence et divergence[modifier | modifier le code]
On cherche à trouver les cas où la série géométrique est convergente, c'est-à-dire où la suite (Sn) est convergente. On va distinguer trois cas (tout en éliminant le cas a = 0 qui est sans intérêt) :
- Si , alors tend vers 0, donc la suite (Sn) est convergente, de limite
Ce calcul permet de résoudre le paradoxe d'Achille et de la tortue énoncé par les Grecs anciens. Il justifie aussi l'égalité 0,9999… = 1 (pour a = 0,9 et q = 110). - Si , on a deux cas. Si q = 1, alors Sn = (n + 1)a et si q = –1, alors Sn = 0 pour n impair et Sn = a pour n pair. La suite diverge dans les deux cas.
- Si , la suite diverge et a fortiori (Sn) diverge grossièrement.
Ces sommes sont dites géométriques, parce qu'elles apparaissent en comparant des longueurs, des aires, des volumes, etc. de formes géométriques dans différentes dimensions.
On dispose donc du résultat général suivant[3],[4],[5],[6],[7] :
La série géométrique réelle de terme initial non nul et de raison est convergente si et seulement si . Dans ce cas, sa somme vaut[8] :
Généralisation au corps des complexes[modifier | modifier le code]
Les résultats s'étendent très naturellement au corps des nombres complexes.
Une série géométrique de premier terme et de raison est la série de terme général .
Une condition nécessaire et suffisante de convergence est, si a est non nul, que la raison q soit un complexe de module strictement inférieur à 1.
Les séries géométriques sont les exemples les plus simples de séries entières dont on dispose. Leur rayon de convergence est 1, et le point 1 est une singularité (et plus précisément, un pôle).
Séries géométriques dans les algèbres de Banach unitaires[modifier | modifier le code]
Si désigne une algèbre de Banach unitaire (réelle ou complexe), d'élément unité e, la série géométrique de raison et de premier terme e est la série de terme général .
La sous-multiplicativité donne : pour tout entier naturel non nul n.
Lorsque , la série géométrique réelle de terme général est convergente, donc la série vectorielle de terme général est absolument convergente.
Notons s sa somme () ; elle commute avec u. Alors :
Donc est inversible dans A dès que , et son inverse est .
C'est un résultat fondamental ; en voici quelques conséquences, énoncées sans démonstration :
- l'ensemble des éléments inversibles de (son groupe des unités) est un ouvert ;
- dans le cas où A est une algèbre de Banach complexe, le spectre de tout élément x de A — l'ensemble des complexes tels que ne soit pas inversible — est une partie fermée non vide et bornée de ℂ ;
- sur son domaine de définition, l'application est développable en série entière.
Notes et références[modifier | modifier le code]
- Pour une légère variante de rédaction, voir .
- Les quinze livres des éléments géométriques d'Euclide, traduction de D. Henrion, 1632, p. 344-345.
- (en) Walter Rudin, Principles of Mathematical Analysis, McGraw-Hill, , 3e éd. (1re éd. 1953) (lire en ligne), p. 61, theorem 3.26.
- (en) Ian Stewart, Calculus : Early Transcendentals, Cengage Learning, , 1344 p. (ISBN 978-0-538-49790-9, lire en ligne), p. 706.
- (en) M. H. Protter et Charles B. Morrey, A First Course in Real Analysis, Springer, , 2e éd. (1re éd. 1977), 536 p. (ISBN 978-0-387-97437-8, lire en ligne), p. 213.
- (en) Charles Chapman Pugh, Real Mathematical Analysis, Springer, , 440 p. (ISBN 978-0-387-95297-0, lire en ligne), p. 180.
- (en) John B. Conway (en), Functions of One Complex Variable I, Springer, coll. « GTM » (no 11), , 2e éd. (1re éd. 1973), 322 p. (ISBN 978-0-387-90328-6, lire en ligne), p. 31.
- Pour une généralisation, voir « Formule du binôme négatif ».
Bibliographie[modifier | modifier le code]
- Éric J.-M. Delhez, Analyse Mathématique, Tome II, Université de Liège, Belgique, , p. 344.
- Mohammed El Amrani, Suites et séries numériques, suites et séries de fonctions, Paris, Ellipses, , 456 p. (ISBN 978-2-7298-7039-3)
- Jean Dieudonné, Éléments d'analyse, t. I : Fondements de l'analyse moderne [détail des éditions]











































