Limite inductive

En mathématiques, et plus particulièrement en théorie des catégories et en algèbre universelle, la notion de limite inductive généralise à des structures la notion classique de limite issue de l'analyse.

Avant-propos

La limite inductive est un cas particulier de colimite en théorie des catégories. Comme sa duale, la limite projective, elle est conceptuellement très proche de la notion de limite rencontrée en analyse et coïncide avec elle dans certains cas.

Un premier point clef est la notion de passage à la limite. Une limite de nombres réels positifs est positive. La limite de la racine carrée est égale à la racine carrée de la limite. De manière analogue^{[réf. nécessaire]}, en algèbre, on va chercher quelles sont les propriétés qui passent à la limite (inductive, projective ou autre). Ces propriétés ne seront pas des fonctions comme en analyse, mais des foncteurs. Ainsi, un foncteur covariant compatible avec la limite inductive fera en sorte que la limite inductive des images soit égale à l'image de la limite inductive. (Si le foncteur est contravariant, il transformera une limite inductive en limite projective.)

Par exemple, dans la catégorie des modules sur un anneau commutatif A, la limite inductive existe toujours et elle est compatible avec le noyau, l'image et le conoyau. Par contre, la limite projective est compatible avec le noyau, mais pas avec l'image.

Certaines structures se construisent naturellement par passage à la limite. Pour une extension algébrique infinie, le groupe de Galois peut se définir par limite projective. On obtient ainsi un groupe profini.

Un deuxième point clef est la notion de densité. Tout nombre réel est limite de nombres rationnels, et même de nombres décimaux (ce qui est la base de la manipulation des nombres à l'aide des calculatrices). Toute fonction continue définie sur un segment est limite uniforme de fonctions polynomiales, et même de fonctions en escalier. Ce résultat permet par exemple une démonstration fulgurante du théorème de Riemann-Lebesgue. On démontre d'abord le résultat pour les fonctions en escaliers et on passe ensuite à la limite. C'est cet état d'esprit que l'on cherche à reproduire en algèbre grâce aux limites inductives^{[réf. nécessaire]}. Au lieu de démontrer directement un résultat, on commence par le démontrer sur des objets simples, puis on passe à la limite inductive. On peut remarquer par exemple que tout espace vectoriel est limite inductive d'espaces vectoriels de dimension finie.

Remarque historique

La notion de limite inductive a été introduite en 1931 par Lev Pontriaguine pour établir l'isomorphisme des quotients par leur sous-groupe de torsion des groupes d'homologie $H_{p}(X;\mathbb {Z} /m\mathbb {Z} )$ et $H_{n-p-1}(\mathbb {R} ^{n}-X;\mathbb {Z} /m\mathbb {Z} )$ (groupes de Betti à valeurs dans $\mathbb {Z} /m\mathbb {Z}$ ; pour $m=0$ un groupe de Betti a pour rang le nombre de Betti correspondant, à savoir son rang) où X est un sous-ensemble compact quelconque de $\mathbb {R} ^{n}$. Les groupes $H_{n-p-1}(\mathbb {R} ^{n}-N(T_{j});\mathbb {Z} /m\mathbb {Z} )$, où $(N(T_{j}))$ est une suite décroissante de complexes simpliciaux compacts d'intersection égale à X, forment un système direct de groupes abéliens, dont $H_{n-p-1}(\mathbb {R} ^{n}-X;\mathbb {Z} /m\mathbb {Z} )$ est le « groupe limite » (« Limesgruppe ») (c'est-à-dire la limite inductive). Pontriaguine a défini de façon tout à fait générale, et comme on le fait aujourd'hui, la limite inductive d'un système direct de groupes (non nécessairement abéliens). Le résultat escompté provient du fait que les applications

$H_{p}(N(T_{j+1});\mathbb {Z} /m\mathbb {Z} )\rightarrow H_{p}(N(T_{j});\mathbb {Z} /m\mathbb {Z} )$, $H_{n-p-1}(\mathbb {R} ^{n}-N(T_{j});\mathbb {Z} /m\mathbb {Z} )\rightarrow H_{n-p-1}(R^{n}-N(T_{j+1});\mathbb {Z} /m\mathbb {Z} )$

sont transposées l'une de l'autre. La suite des $H_{p}(N(T_{j});\mathbb {Z} /m\mathbb {Z} )$ forme un système inverse dont la limite (projective) est $H_{p}(X;\mathbb {Z} /m\mathbb {Z} )$ ; néanmoins, Pontriaguine a manqué la notion de limite projective, entrevue par Eduard Čech l'année suivante (1932) indépendamment du travail de Pontriaguine ; mais la définition précise de la limite projective d'un système inverse d'espaces topologiques n'a été donnée qu'en 1936 par Norman Steenrod. La formulation des limites projectives (resp. inductives) de groupes, ou de groupes topologiques, ou d'espaces topologiques, etc. en tant que foncteurs entre la catégorie des systèmes directs (resp. inverses) et la catégorie concrète des groupes, ou des groupes topologiques, ou des espaces topologiques, etc., a été réalisée en 1945 par Samuel Eilenberg et Saunders Mac Lane ; ces notions et leurs relations ont été formulées de manière complètement générale et étudiées en détail par Daniel Kan en 1958.

Ensemble ordonné filtrant

Soit $(I,\leq )$ un ensemble ordonné (partiellement ordonné en général). On dit que $(I,\leq )$ est un ensemble ordonné filtrant si

$\forall (i,j)\in I^{2},\exists k\in I,i\leq k\ et\ j\leq k.$

On dit qu'un ensemble est filtrant à gauche lorsque l'ordre opposé est filtrant. Dans un tel cas, on conservera le vocabulaire mais il correspondra à l'ordre opposé. Dans la pratique, cela n'engendre pas de confusion, c'est même plutôt pratique. Un ensemble filtrant I est une catégorie dont les objets sont les éléments de I et les morphismes sont les couples $(j,i),i\leq j$ (de source i et de but j).

Système inductif

Soit $(I,\leq )$ un ensemble ordonné filtrant. Soit ${\mathcal {C}}$ une catégorie. On appelle système inductif ${\mathfrak {D}}$ d'objets de ${\mathcal {C}}$ indexés par I un foncteur (covariant) de I dans ${\mathcal {C}}$, la donnée d'une famille $(E_{i})_{i\in I}$ d'objets de ${\mathcal {C}}$ et de morphismes $f_{i}^{j}:E_{i}\to E_{j}$ pour chaque couple d'indices $(i,j)\in I^{2}$ tel que $i\leq j$, le tout vérifiant :

• $\forall i\in I,f_{i}^{i}=Id_{E_{i}}$ ;
• $\forall (i,j,k)\in I^{3},\ i\leq j\leq k\Rightarrow f_{j}^{k}\circ f_{i}^{j}=f_{i}^{k}$.

Ce foncteur est défini par ${\mathfrak {D}}(i)=E_{i}$ et ${\mathfrak {D}}((i,j))=f_{i}^{j}$.

Propriété universelle de la limite inductive

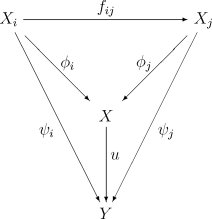
Soit (X_i, f_ij) un système inductif dans une catégorie ${\mathcal {C}}$. La limite inductive X, lorsqu'elle existe, est un objet de la catégorie ${\mathcal {C}}$ muni de flèches $\phi _{i}$ de X_i à valeurs dans X vérifiant les relations de compatibilité $\phi _{i}=\phi _{j}\circ f_{ij}$ pour tous $i\leq j$. De plus, la donnée $(X,\phi _{i})$ doit être universelle : pour tout autre objet Y muni d'une famille de flèches ψ_i vérifiant des compatibilités analogues, il existe une unique flèche u : X → Y telle que le diagramme :

soit commutatif pour tous i ≤ j. La limite inductive est notée : $X=\varinjlim X_{i}$. On parlera de limite inductive des X_i suivant les morphismes de transition f_ij, ou par abus de langage, de limite suivant I, voir tout simplement de limite inductive des X_i.

Comme pour toute propriété universelle, lorsqu'elle existe, la limite inductive est unique, à isomorphisme unique près.

Autrement dit, la limite inductive représente le foncteur qui à un objet Y de la catégorie ${\mathcal {C}}$ associe l'ensemble $\varprojlim Hom(X_{i},Y)$.

Construction de la limite inductive

La limite inductive existe dans la plupart des catégories usuelles (notamment les magmas, monoïdes, groupes, groupes abéliens, anneaux, A-modules, K-espaces vectoriels, espaces topologiques, etc.). On peut la construire à partir de la limite inductive de la famille d'ensembles sous-jacents. Elle commute donc avec le foncteur d'oubli.

De façon plus générale, dans une catégorie quelconque, sa construction est duale de celle de limite projective. On construit la limite projective à l'aide de deux processus, celui de produit et celui de noyau. On construit la limite inductive à partir des deux notions duales de somme et de conoyau.

Limite inductive d'ensembles

Soit (E_i, f_ij) un système inductif d'ensembles. On obtient la limite inductive comme ensemble quotient de l'union disjointe $\sqcup _{i\in I}E_{i}$ par la relation d'équivalence :

$(i,x)\sim (j,y)\Leftrightarrow \exists k\in I,i\leq k,\ j\leq k\ et\ f_{i}^{k}(x)=f_{j}^{k}(y)$

Notons $E_{\infty }$ l'ensemble quotient. Pour définir $\phi _{i}:E_{i}\to E_{\infty }$, on prend comme $\phi _{i}(x)$ la classe de $(i,x)$.

Limite inductive d'espaces topologiques

Soit (E_i, f_ij) un système inductif d'espaces topologiques. Dans la construction précédente, on munit successivement la réunion disjointe des ensembles sous-jacents de la topologie finale, puis l'ensemble quotient, de la topologie quotient (ou plus directement : on munit la limite inductive ensembliste de la topologie finale).

Limite inductive de magmas

Soit (E_i, f_ij) un système inductif de magmas. Chaque ensemble $E_{i}$ est muni d'une loi de composition interne $*_{i}$ et chaque application $f_{i}^{j}$ est un morphisme. On commence par construire la limite inductive des ensembles $E_{i}$. Il existe alors une unique structure de magma sur $E_{\infty }$ telle que les applications canoniques $\phi _{i}$ soient des morphismes.

On construit cette loi de la façon suivante. Soit $(i,x)$ et $(j,y)$ deux représentants de deux éléments de $E_{\infty }$. Il existe $k\in I$ tel que $i\leq k$ et $j\leq k$. Dans $E_{\infty }$, on a $(i,x)=(k,f_{i}^{k}(x))$ et $(j,y)=(k,f_{j}^{k}(y))$. On pose alors $(i,x)*(j,y)=(k,f_{i}^{k}(x)*_{k}f_{j}^{k}(y))$, le résultat obtenu ne dépend bien sûr pas du choix de $k$.

Propriétés

• Si chaque loi $*_{i}$ est commutative, alors la loi * est commutative.
• Si chaque loi $*_{i}$ est associative, alors la loi * est associative.
• Si chaque loi $*_{i}$ possède un élément neutre $e_{i}$ et si chaque morphisme $f_{i}^{j}$ vérifie $f_{i}^{j}(e_{i})=e_{j}$, alors * possède un neutre e (de plus, pour chaque i, on a $\phi _{i}(e_{i})=e$).
• Si chaque $E_{i}$ possède une structure de groupe, $E_{\infty }$ est un groupe.

Limite inductive d'anneaux

De façon analogue, si chaque ensemble $E_{i}$ est muni de deux lois $+_{i}$ et $*_{i}$, la limite inductive $E_{\infty }$ est munie de deux lois $+$ et $*$. Si chaque loi $*_{i}$ est distributive par rapport à $+_{i}$, alors $*$ est distributive est par rapport à $+$.

Ce procédé permet ainsi de construire une limite inductive d'anneau.

• Si chaque anneau $E_{i}$ est intègre, il en est de même de $E_{\infty }$.
• Si chaque anneau $E_{i}$ est un corps, il en est de même de $E_{\infty }$.

Limite inductive de modules

Soit A un anneau commutatif et (E_i, f_ij) un système inductif de A-modules. On peut munir la limite inductive $E_{\infty }$ des ensembles sous-jacents d'une structure de A-module de sorte que les applications $\phi _{i}$ soient linéaires. Une telle structure est unique et se construit de la même façon que pour les magmas.

Exemples

• Si l'ensemble filtrant I possède un plus grand élément $\omega$ (par exemple si I est fini et non vide), la limite inductive de tout système inductif $(E_{i},f_{i}^{j})$ est égale à $E_{\omega }$.
• La limite inductive du système indexé par l'ensemble vide est l'objet initial.
• Soit E un ensemble et $(E_{n})$ une suite croissante de sous-ensembles de E, avec les injections canoniques. La limite inductive de la suite $(E_{n})$ s'identifie à la réunion de ces ensembles.
• Soit p un nombre premier. Pour tout n soit U_n le groupe cyclique des racines pⁿ-ièmes de l'unité dans un corps algébriquement clos. On considère les inclusions comme morphismes de transition. La limite inductive de ce système est alors le groupe infini constitué de toutes les racines p-primaires de l'unité (voir Groupe de Prüfer).
• Soit p un nombre premier. Pour tout entier n non nul, soit $\mathbb {K} _{n}$ le corps fini $\mathbb {F} _{p^{n}}$ ayant $p^{n}$ éléments. On ordonne l'ensemble $\mathbb {N} ^{\star }$ par la relation de divisibilité. Alors la clôture algébrique de $\mathbb {F} _{p}=\mathbb {Z} /p\mathbb {Z}$ est la limite inductive des $\mathbb {K} _{n}$.
• Soit E un espace topologique et a un point de E, le germe en a des fonctions de E dans $\mathbb {R}$ est la limite inductive des ensembles $C(U,\mathbb {R} )$ des applications continues d'un voisinage quelconque U de a, les voisinages étant ordonnés par l'inclusion (filtrante à gauche, ce qui inverse le sens des flèches) : pour $V\subset U$, on va de $C(U,\mathbb {R} )$ dans $C(V,\mathbb {R} )$ par restriction.

Sources

• Régine et Adrien Douady, Algèbre et théories galoisiennes [détail des éditions]
• N. Bourbaki, Algèbre, chapitres 1 à 3