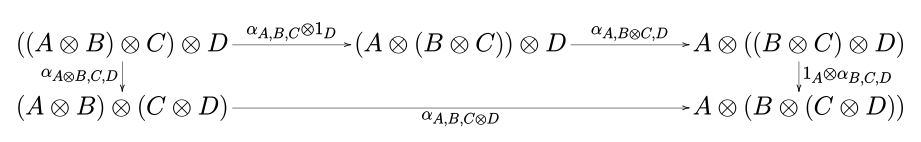Catégorie monoïdale
En mathématiques, une catégorie monoïdale est une catégorie munie d'un bifoncteur qui généralise la notion de produit tensoriel de deux structures algébriques. Intuitivement, il s'agit de l'analogue, au niveau des catégories, de la notion de monoïde, c'est-à-dire que le bifoncteur joue le rôle d'une sorte de multiplication pour les objets de la catégorie.
Définition[modifier | modifier le code]
Une catégorie monoïdale est une catégorie munie :
- D'un bifoncteur appelé produit tensoriel.
- D'un objet I appartenant à appelé « objet unité ».
- D'un isomorphisme naturel α appelé « associateur » tel que pour tous objets A, B et C, αA,B,C soit un isomorphisme de vers . Autrement dit, α est un isomorphisme naturel du foncteur vers le foncteur .
- De deux isomorphismes naturels λ et ρ induisant, pour tout objet A, des isomorphismes et .
Les conditions de cohérence pour ces transformations naturelles s'expriment par la commutativité des diagrammes suivants, appelés respectivement identité du triangle et identité du pentagone.
Exemples[modifier | modifier le code]
- La catégorie des ensembles Set munie du produit cartésien, est une catégorie monoïdale. Une unité est donnée par un singleton.
- La catégorie des ensembles Set munie de la réunion disjointe, est une catégorie monoïdale. L'unité est donnée par l'ensemble vide.
- Si k est un corps commutatif, la catégorie des k-espaces vectoriels munie du produit tensoriel usuel est une catégorie monoïdale. Une unité est donnée par k.
- Plus généralement, si R est un anneau commutatif, la catégorie des R-modules munie du produit tensoriel usuel est une catégorie monoïdale. Une unité est donnée par R.
- La catégorie des espaces vectoriels munie de la somme directe est une catégorie monoïdale, l'unité étant donnée par le singleton réduit au vecteur nul.
- Si A est une algèbre associative, la catégorie des A-modules n'est pas une catégorie monoïdale en général. Il faut des conditions supplémentaires sur A, par exemple que A soit une algèbre de Hopf.