Cône de révolution
Le terme de cône circulaire droit ou cône de révolution s'applique à deux types d'objets mathématiques : une surface et un solide
- comme surface, il s'agit de la surface engendrée par la révolution d'une droite sécante à un axe fixe autour de ce dernier. Il s'agit d'un cas particulier de cône. Les coniques forment une famille très utilisée de courbes planes algébriques résultant de l'intersection d'un plan avec un cône de révolution.
- comme solide, il s'agit du solide de révolution engendré par la rotation d'un triangle rectangle autour d'un des côtés de l'angle droit. Le solide délimité par un tel cône et deux plans perpendiculaires à son axe de révolution est appelé un tronc de cône.
Équations et paramétrisation de la surface de révolution[modifier | modifier le code]

Dans un repère orthonormé de l'espace, le cône engendré par la rotation d'une droite passant par O autour de l'axe (Oz) est l'ensemble des points de coordonnées cylindriques vérifiant l'équation :
où est l'angle entre la droite et l'axe (demi-angle au sommet du cône).
On en déduit l'équation en coordonnées cartésiennes :
Ainsi que la paramétrisation : .
Propriétés associées au solide de révolution[modifier | modifier le code]
| Cône de révolution | |
 Tronc de cône de révolution de base de rayon r de hauteur h, et de demi-angle au sommet . | |
| Type | Solide de révolution |
|---|---|
| Faces | 1 face circulaire et une surface conique |
| Volume | π r 2 h3 |
| Aire | (surface latérale) : π r √(r 2 + h 2) |
| Propriétés | Constructible |
| modifier |
|
Aire et volume d'un cône solide[modifier | modifier le code]
Aire latérale et volume du cône solide (tronc de cône délimité par un demi cône et un plan à une distance h du sommet, coupant le cône suivant un cercle de rayon r) :
Aire latérale et volume d'un tronc de cône[modifier | modifier le code]
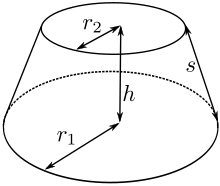
Dans le cas général, si les deux plans, distants de h coupent le cône suivant deux cercles de rayon r1 et r2, l'aire latérale et le volume valent [1] :
Relations entre le tronc de cône et son patron[modifier | modifier le code]

- La surface latérale d'un tronc de cône de hauteur h et de rayon de base r a pour patron plan un disque de rayon R dans lequel on a découpé un secteur d'angle .
- La relation entre R, r et est alors : . En éliminant r entre cette relation et , on obtient : .
- La relation entre et est : .
Tronc de cône de volume maximal pour un rayon de patron donné[modifier | modifier le code]
Partant de la formule , on obtient que le volume maximal à R fixé est obtenu pour .
Le volume maximal vaut donc , et le demi-angle au sommet, est l'angle dit « magique » (voir la suite A195696 de l'OEIS) ; l'angle au centre du secteur de disque est .
Tronc de cône de volume maximal pour une aire latérale donnée[modifier | modifier le code]
Partant de la formule , on obtient que le volume maximal à A fixé est obtenu pour [2], soit pour , complémentaire de l'angle magique précédent (voir la suite A195695 de l'OEIS) ; l'angle au centre du secteur de disque est alors .
Notes et références[modifier | modifier le code]
- GIECK, Formulaire technique, 10e édition, 1997, C2
- (en) John D. Barrow, « Outer space: Archimedean ice cream cones », sur plus.math.org (consulté le )


























