Dodécaèdre adouci

Dodécaèdre adouci

Éléments

Faces	Arêtes	Sommets
92 triangles et pentagones	150	60 de degré 5

Données clés

Type	Solide d'Archimède
Caractéristique	2
Propriétés	Semi-régulier et convexe, chiral
Groupe de symétrie	Ih
Dual	Hexacontaèdre pentagonal

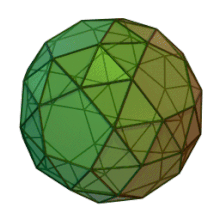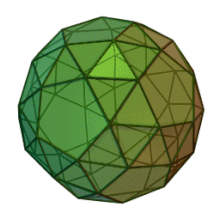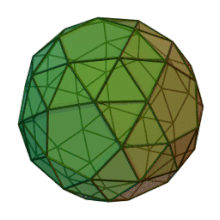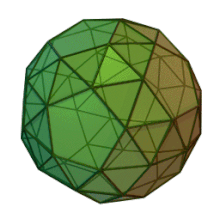
Le dodécaèdre adouci ou icosidodécaèdre adouci est un solide d'Archimède.

Le dodécaèdre possède 92 faces dont 12 sont des pentagones et les 80 autres sont des triangles équilatéraux. Il possède aussi 150 arêtes et 60 sommets. Il a deux formes distinctes, qui sont les images dans un miroir (ou énantiomorphes) l'une de l'autre.

Relations géométriques

Le dodécaèdre peut être engendré en prenant les douze faces pentagonales du dodécaèdre, en les tirant de telle façon qu'aucune ne se touchent, puis en leur donnant toutes une petite rotation de leurs centres (toutes en sens horaire (Sh) ou toutes en sens anti-horaire (Sah)) jusqu'à ce que l'espace entre elles puisse être rempli par des triangles équilatéraux.

Coordonnées cartésiennes

Les coordonnées cartésiennes pour les sommets d'un dodécaèdre adouci sont toutes les permutations paires de

$(\pm 2\alpha ,\pm 2,\pm 2\beta )\,$,

$\left(\pm \left(\alpha +{\frac {\beta }{\varphi }}+\varphi \right),\pm \left(-\alpha \varphi +\beta +{\frac {1}{\varphi }}\right),\pm \left({\frac {\alpha }{\varphi }}+\beta \varphi -1\right)\right)$,

$\left(\pm \left(-{\frac {\alpha }{\varphi }}+\beta \varphi +1\right),\pm \left(-\alpha +{\frac {\beta }{\varphi }}-\varphi \right),\pm \left(\alpha \varphi +\beta -{\frac {1}{\varphi }}\right)\right)$,

$\left(\pm \left(-{\frac {\alpha }{\varphi }}+\beta \varphi -1\right),\pm \left(\alpha -{\frac {\beta }{\varphi }}-\varphi \right),\pm \left(\alpha \varphi +\beta +{\frac {1}{\varphi }}\right)\right)$ et

$\left(\pm \left(\alpha +{\frac {\beta }{\varphi }}-\varphi \right),\pm \left(\alpha \varphi -\beta +{\frac {1}{\varphi }}\right),\pm \left({\frac {\alpha }{\varphi }}+\beta \varphi +1\right)\right)$,

avec un nombre pair de signes plus, où

$\alpha =\xi -{\frac {1}{\xi }}$

et

$\beta =\xi \varphi +\varphi ^{2}+{\frac {\varphi }{\xi }}$,

où $\varphi ={\frac {1+{\sqrt {5}}}{2}}$ est le nombre d'or et $\xi \,$ est la solution réelle de $\xi ^{3}-2\xi =\varphi \,$, qui est le nombre

$\xi ={\sqrt[{3}]{{\frac {\varphi }{2}}+{\frac {1}{2}}{\sqrt {\varphi -{\frac {5}{27}}}}}}+{\sqrt[{3}]{{\frac {\varphi }{2}}-{\frac {1}{2}}{\sqrt {\varphi -{\frac {5}{27}}}}}}$

ou approximativement 1,7155615.

On notera que, parmi les 6 permutations de 3 coordonnées, les permutations paires sont les 3 permutations circulaires.

Prendre les permutations impaires des coordonnées ci-dessus, ou^{[réf. nécessaire]} les mêmes permutations avec un nombre impair de signes plus, donne une autre forme, l'énantiomorphe de celle-ci.

Patron (géométrie).

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Snub dodecahedron » (voir la liste des auteurs).

dont la seule référence était (en) Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979 (ISBN 0-486-23729-X).

Voir aussi

Article connexe

Polyèdre adouci

Liens externes

• Dodécaèdre adouci sur MathCurve.
• (en) Vincent Herr, « Modèle en fil de fer d'un dodécaèdre adouci irrégulier », 2004