Papyrus Rhind

Papyrus Rhind

Détail d'une des deux principales parties du papyrus Rhind, British Museum, EA 10057.

Matériau	papyrus

Le papyrus Rhind est un célèbre papyrus de la Deuxième Période intermédiaire qui a été écrit par le scribe Ahmès.

Son nom vient de l'Écossais Alexander Henry Rhind qui l'acheta en 1858 à Louxor, mais il aurait été découvert par des pilleurs sur le site de la ville voisine de Thèbes. Depuis 1865, il est conservé au British Museum (à Londres). Avec le papyrus de Moscou, il est une des sources les plus importantes concernant les connaissances mathématiques dans l'Égypte antique.

Ahmès indique que son papyrus est, en partie, une copie de résultats plus anciens remontant au Moyen Empire (vers 2000 av. J.-C.). Le papyrus Rhind contient 87 problèmes résolus d'arithmétique, d'algèbre, de géométrie et d'arpentage, sur plus de cinq mètres de longueur et trente-deux centimètres de large. Il est rédigé en écriture hiératique.

Le papyrus

Un extrait du papyrus Rhind.

Description

Le papyrus Rhind se présentait à l'origine comme un rouleau constitué de quatorze feuilles soigneusement assemblées. Il est actuellement séparé en deux bandes de 32 cm de hauteur, l'une de 299,5 cm de long (BM 10057) et l'autre de 195,5 cm de long (BM 10058) toutes deux conservées au British Museum qui les a acquises en 1865, auprès de l'exécuteur testamentaire d'Alexander Henry Rhind. Ces bandes étaient à l'origine solidaires et reliées par un morceau manquant de 18 cm. Des fragments de ce dernier ont été identifiés aux États-Unis en 1922 par Percy Edward Newberry, ils se trouvent aujourd'hui au Brooklyn Museum à New York. Malgré quelques lacunes, le papyrus est quasiment complet. Il se déroule en une succession de pages de la droite vers la gauche, écrites en hiératique (également de la droite vers la gauche). Le recto du papyrus est presque entièrement utilisé, avec quelques parties intermédiaires laissées vierges. Le verso est utilisé sur la première section (BM 10058), celle la plus à droite dans l'ordre de lecture, mais ne l'est pas sur la seconde section (BM 10057), en dehors de quelques inscriptions ajoutées vraisemblablement après la composition originelle.

Découverte

Selon l'édition du fac-similé du papyrus publiée en 1898 par le British Museum, celui-ci a été découvert près du Ramesséum sur le site de Thèbes. Les deux principales sections, probablement découpées par les pilleurs, ont été achetées en 1858 par Rhind (à Louxor), les fragments de la petite partie intermédiaire en 1862 ou 1863 par le collectionneur américain Edwin Smith.

Origine et datations

Le texte signé par le scribe Ahmès est daté par celui-ci de l'an 33 du règne du pharaon Apophis, souverain Hyksôs de la XV^e dynastie, qui règne en Basse-Égypte à Avaris dans la première moitié du XVI^e siècle avant notre ère, à la fin de la Deuxième Période intermédiaire. Ahmès annonce en introduction que le texte est une copie d'une version précédente datant d'un pharaon dont une partie du nom est effacée, mais qui parait être Amenemhat III, pharaon de la XII^e dynastie qui vivait près de trois siècles auparavant, à l'époque du Moyen Empire.

Le papyrus porte au verso, dans la partie centrale de BM 10057, de brèves inscriptions manifestement ajoutées après la composition, et datées de la onzième année du règne d'un pharaon inconnu. Elles font référence aux événements ayant conduit à la chute d'Avaris (celle-ci même n'est pas mentionnée) qui marque la fin des souverains Hyksôs chassés d'Égypte par le souverain de Thèbes (et futur pharaon de l'Égypte réunifiée) Ahmôsis. Leur interprétation est objet de débats. Si ces inscriptions ont été ajoutées avant le transfert du papyrus à Thèbes, la date pourrait renvoyer au règne de Khamoudy dernier roi Hyksôs de Basse-Égypte. Le papyrus aurait alors pu être apporté d'Avaris à Thèbes par l'armée victorieuse d'Ahmôsis, ce qui explique alors la découverte dans la capitale de la Haute-Égypte d'un papyrus originaire de Basse-Égypte.

Usage

Tant la taille que le soin apporté à la composition et le peu d'erreurs relevées dans le texte témoignent de la qualité du document, qui est probablement un manuel de référence de haut niveau utilisé pour enseigner dans une école de scribes. En cela il est très différent du papyrus de Moscou, la seconde source en importance pour les mathématiques égyptiennes du Moyen Empire, plus ancien mais qui ressemble plutôt à une copie d'étudiant d'un manuel comparable au papyrus Rhind.

Application

Le papyrus oriente ces problèmes notamment pour aider à la quantification de grain ou à une répartition équitable ou inéquitable des pains parmi les hommes.

Toutefois les calculs exhibés auraient pu prendre un sens très concret pour des mesures qui cumulent des rapports de un à n, même si ces questions ne sont pas explicitement abordées par le papyrus :

• Pour les mesures de distance, les formules de calcul ont pu avoir du sens pour mesurer des distances si les Égyptiens connaissaient les formes élémentaires de théorème de Thalès déjà connues depuis la Première dynastie de Babylone entre 1900 et 1600 avant notre ère, d'après la tablette MLC 1950.

• Pour les mesures de poids, les formules de calcul ont pu avoir du sens si les Égyptiens ont connu des formes rudimentaires de balance romaine, chaque rapport de 1 à n pouvait être considéré comme une mesure.

Contenu

Après une large bordure verticale qui contient entre autres le titre, la date et le nom de l'auteur, le papyrus est divisé recto et verso par sept lignes noires en six bandes horizontales. L'écriture est réalisée à l'encre noire et à l'encre rouge. Cette dernière sert à mettre en valeur les débuts de section et certains points du texte.

Depuis la première édition d'August Eisenlohr, le papyrus est traditionnellement divisé, outre le bloc de titre, en une table de divisions de 2 par n, pour une entier impair n variant de 3 à 101, suivie de 87 blocs traditionnellement appelés « problèmes », numérotés de 1 à 87, auxquels s'ajoutent 7B, 59B, 61B, et 82B.

Cartographie du papyrus Rhind selon Chace, Bull et Manning 1929.

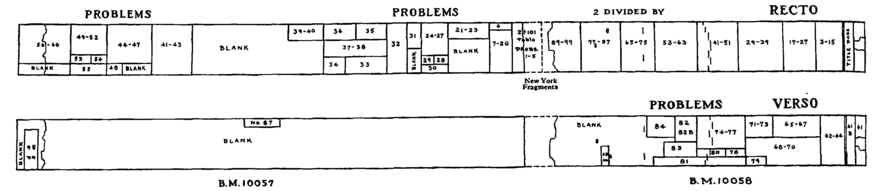
Mais les numéros de 85 à 87 n'ont pas de contenu mathématique, ce sont des additions ultérieures. Le numéro 85 est un assemblage de signes incompréhensible, le numéro 86 rassemble des fragments de compte résultant d'une réparation ancienne avec réemploi d'un autre papyrus et les quelques notes du numéro 87 évoquent la prise d'Avaris par Ahmôsis.

Les numéros de 7 à 20 et le numéro 61 sont eux plutôt des calculs, qui pourraient servir à la création de tables, les numéros 80 et 81 sont plutôt des tables, et les numéros de 82 à 84 des modèles de compte.

Restent donc 64 vrais problèmes, et même 66 avec les numéros 59B et 61B.

Table de divisions de 2

La table d'expressions de 2 donne la division de 2 par un nombre impair compris entre trois et cent-un, sous la forme de somme de fractions de l'unité, en maintenant un diviseur assez faible.

Pour chacun des diviseurs, une formule similaire est ainsi proposée :

${\frac {2}{n}}={\frac {1}{a_{1}}}+{\frac {1}{a_{2}}}+{\frac {1}{a_{3}}}+{\frac {1}{a_{4}}}$

Mais parfois, la formule peut n'être écrite qu'avec deux ou trois opérandes, au lieu de quatre.

D'une manière plus moderne, le problème peut s'écrire :

${\frac {2}{N-x}}={\frac {x}{PPCM(N,N-x)}}$ avec

$x=x_{1}+x_{2}+x_{3}+x_{4}$

$x_{i}\ {\text{divise}}\ N$ de sorte que : $PPCM(N,N-x)=x_{i}a_{i}$

$x_{i}\neq x_{j}$

Cette formule montre que la solution dépend de la divisibilité du $n$.

Cette formule conduit généralement à ce que a soit supérieur (ou égal à n), et à ce que a soit généralement un nombre composé : les nombres 12, 20, 24, 30, 40 et 60 qui sont multiples de 2, 3, 4, ou 5 reviennent facilement.

Les connaissances modernes permettent de savoir qu'un nombre rationnel peut s'écrire d'une infinité de manières comme la somme de fractions de l'unité.

Plusieurs personnes se sont demandé comment les Égyptiens avaient pu obtenir cette table.

Des suggestions de Gillings ont proposé cinq techniques différentes. Le problème 61 du Papyrus Rhind donne une formule : ${\frac {2}{3n}}={\frac {1}{2n}}+{\frac {1}{6n}}$, dont on peut déclarer qu'elle est l'équivalent de ${\frac {2}{n}}={\frac {1}{2}}{\frac {1}{n}}+{\frac {3}{2}}{\frac {1}{n}}$ (n divisible par 3 dans la dernière équation).

On compte d'autres possibles formules, telles que :

${\frac {2}{n}}={\frac {1}{3}}{\frac {1}{n}}+{\frac {5}{3}}{\frac {1}{n}}$ (n divisible par 5)

${\frac {2}{mn}}={\frac {1}{m}}{\frac {1}{k}}+{\frac {1}{n}}{\frac {1}{k}}$ (où k est la moyenne de m et de n)

${\frac {2}{n}}={\frac {1}{n}}+{\frac {1}{2n}}+{\frac {1}{3n}}+{\frac {1}{6n}}$ Cette formule porte la décomposition pour n = 101 dans la table.

David M. Burton a suggéré qu'Ahmès a utilisé deux méthodes différentes pour convertir 2/p (où p est un nombre premier), et trois méthodes pour convertir 2/pq dénominateurs composés. D’autres suggestions proposent qu'Ahmès qui n'a utilisé qu'une seule méthode : l'emploi de facteurs multiplicatifs réductibles au plus petit commun multiple^{[réf. nécessaire]}.

Algorithmes de multiplication et division (problèmes 1 à 23)

Ces problèmes permettent de comprendre les techniques de multiplication et de division chez les Égyptiens.

Résolution d'équations par la méthode de fausse position (problèmes 24 à 34)

Voir Résolutions d'équations.

Les problèmes d'arpentage (problèmes 41 à 60)

Le disque de diamètre neuf a une aire voisine du carré de côté huit.

L'arpentage, mesure des distances et les problèmes géométriques qui lui sont liés sont également abordés : aires planes (du trapèze en particulier), volumes de greniers à grains, calcul de pyramides.

Les problèmes 56, 57, 58, 59 et 60, sont consacrés à des calculs relatifs à la pente d'une pyramide, mesurée par leur seqed (sḳd), qui correspond à la demi base de la pyramide divisée par sa hauteur, autrement dit il s'agit de la cotangente de l'angle que forme la ligne de plus grande pente d'une face avec l'horizontale. Le seqed est mesuré par le déplacement horizontal nécessaire pour rejoindre la face après une élévation verticale d'une coudée, il s'exprime donc avec les unités de longueur en usage, coudée, paume, le septième d'une coudée, et doigt qui vaut le quart d'une paume. Pour quatre de ces problèmes le seqed est de cinq paumes et un doigt. La cotangente est donc de (1/7) × (5+1/4) = 3/4 (ce qui correspond à une pente de 4/3).

Le triangle rectangle correspondant à cette pente, de côtés de l'angle droit proportionnels à trois et quatre, est donc un triangle 3-4-5. Cependant le papyrus Rhind ne traite que de la pente, et de fait le triangle 3-4-5 n'y est jamais mentionné. Cette inclinaison a été clairement choisie pour certaines pyramides de la VI^e dynastie, dont la base a pour côté cent-cinquante coudées et la hauteur cent coudées. Sans que ce soit aussi manifestement intentionnel, celle de la pyramide de Khéphren en est proche. Il est tout à fait possible que le triangle et ses proportions aient été remarqués ; celles-ci facilitent la réalisation d'équerres triangulaires en bois qui auraient pu être utilisées pour vérifier la pente, mais cela reste hypothétique.

Au problème 50, Ahmes expose une procédure pour calculer l'aire d'un disque connaissant son diamètre : au diamètre est soustrait 1/9 de celui-ci, puis le résultat est élevé au carré. La méthode est exposée pour un diamètre ad hoc de 9 khet, ce qui donne une aire de 64 setjat. On peut y voir une première approche de la quadrature du cercle, la construction d'un carré de même aire qu'un disque donné : l'aire du disque de diamètre d est ramenée à celle d'un carré de côté 8d/9.

En d'autres termes, l'aire d'un disque de diamètre 9 unités est sensiblement égale à celle d'un carré de 8 unités de côté. Pour se faire une meilleure idée du degré de précision ainsi obtenu, on peut remarquer que cette construction correspond implicitement à une approximation de notre nombre π pour le calcul de l'aire du disque de 256/81 ≈ 3,160, une approximation inférieure à 0,6 %.

Mais le papyrus Rhind ne fournit aucune constante multiplicative, telle qu'une approximation de π, pour calculer l'aire du disque. La seule constante qui est utilisée dans la procédure est 1/9

Contenu détaillé

Cette table résume le contenu du papyrus Rhind en langage moderne. Elle se base sur l'exposition en deux volumes du papyrus qui a été publiée par Arnold Buffum Chace en 1927, et en 1929.

Le papyrus se compose de quatre sections : une page de titre, la table 2/n, un petit « tableau 1-9/10 » et 91 problèmes. Ces derniers sont numérotés de 1 à 87 et comprennent quatre éléments mathématiques qui ont été désignés par les modernes comme problèmes 7B, 59B, 61B et 82B. Les numéros 85 à 87, quant à eux, ne sont pas des éléments mathématiques faisant partie du corps du document, mais sont respectivement : une petite phrase terminant le document, un morceau de « papier brouillon » utilisé pour maintenir le document ensemble (contenant un écrit sans rapport), et une note historique qui est censée décrire une période peu de temps après l'achèvement du corps du papyrus. Ces trois derniers éléments sont écrits sur des zones disparates du verso du papyrus, loin du contenu mathématique. Chace les différencie donc en les qualifiant de « numéros » par opposition à « problèmes », comme les 88 autres éléments numérotés.

Section des problèmes (résolus) numérotés	Description du problème, ou description	Solution, ou description	Notes
Page de titre (Title Page)	Ahmès s'identifie lui et les circonstances historiques.	« Calculs précis. L'entrée dans la connaissance de toutes les choses existantes et tous les secrets obscurs. Ce livre a été copié en l'année 33, durant le quatrième mois de la saison d’inondation(s), sous le règne du roi de Haute et Basse-Égypte, 'A-user-Re', doté de la vie, au désir des écritures anciennes faite au temps du roi de Haute et Basse-Égypte, Ne-ma'en-Rê. C'est le scribe Ahmès qui copie cette écriture. »	Il est clair d'après la page de titre qu'Ahmès identifie à la fois sa période, et celle du texte ancien ou des textes qu'il est supposé avoir copié, créant ainsi le papyrus Rhind. Le papyrus est écrit des deux côtés - c'est-à-dire sur le recto et le verso. Voir l'image pour les détails.
Fractions de deux (table 2/n)	Exprime chacune des fractions de deux pour les dénominateurs impairs compris entre trois et cent-un sous forme d'une somme de fractions de un, dites fractions égyptiennes.	Voir l'article table d'expressions de 2 du papyrus Rhind pour un résumé et des solutions de cette section.	Au travers du papyrus, la plupart des solutions sont données sous la forme de représentation particulière de fractions égyptiennes d'un nombre rationnel. Cependant, puisque chaque rationnel positif peut être représenté d'une manière infinie sous la forme de fractions égyptiennes, ces solutions ne sont pas uniques. La fraction 2/3 est la seule exception utilisée en complément des entiers qu'Ahmès utilise avec toutes les fractions rationnelles d'unité positive pour exprimer les fractions égyptiennes. La table 2/n peut être considérée comme suivant partiellement un algorithme (voir problème 61B) pour exprimer 2/n comme fraction égyptienne de deux termes, quand n est composé. Cependant, cet algorithme fledgling est transformé de côté dans plusieurs situations lorsque n est un nombre premier. La méthode d'élaboration de la table 2/n, donc, suggère aussi des débuts dans la théorie des nombres et pas seulement en arithmétique .
Table des dixièmes (table 1-9/10)	Écriture des quotients depuis un dixième jusqu'à neuf dixièmes sous forme de développement égyptien.	${\frac {1}{10}}={\frac {1}{10}}\;\;\;;\;\;\;{\frac {2}{10}}={\frac {1}{5}}\;\;\;;\;\;\;{\frac {3}{10}}={\frac {1}{5}}+{\frac {1}{10}}$ ${\frac {4}{10}}={\frac {1}{3}}+{\frac {1}{15}}\;\;\;;\;\;\;{\frac {5}{10}}={\frac {1}{2}}\;\;\;;\;\;\;{\frac {6}{10}}={\frac {1}{2}}+{\frac {1}{10}}$ ${\frac {7}{10}}={\frac {2}{3}}+{\frac {1}{30}}\;\;\;;\;\;\;{\frac {8}{10}}={\frac {2}{3}}+{\frac {1}{10}}+{\frac {1}{30}}\;\;\;;\;\;\;{\frac {9}{10}}={\frac {2}{3}}+{\frac {1}{5}}+{\frac {1}{30}}$	-
Problèmes 1 à 6	Partage du pain parmi dix hommes en 1, 2, 6, 7, 8 et 9 fractions. Dans chaque cas, la part de chaque homme est représentée sous la forme développement égyptien.	${\frac {1}{10}}={\frac {1}{10}}\;\;\;;\;\;\;{\frac {2}{10}}={\frac {1}{5}}$ ${\frac {6}{10}}={\frac {1}{2}}+{\frac {1}{10}}\;\;\;;\;\;\;{\frac {7}{10}}={\frac {2}{3}}+{\frac {1}{30}}$ ${\frac {8}{10}}={\frac {2}{3}}+{\frac {1}{10}}+{\frac {1}{30}}\;\;\;;\;\;\;{\frac {9}{10}}={\frac {2}{3}}+{\frac {1}{5}}+{\frac {1}{30}}$	les six premiers problèmes du papyrus sont de simples répétitions de l'information déjà décrite dans la table des dixièmes, maintenant présentés sous la forme de problèmes.
7, 7B, 8 à 20	Soit $S=1+1/2+1/4={\frac {7}{4}}$ et $T=1+2/3+1/3=2$. Pour les multiplications suivantes, écriture du produit sous forme de développement égyptien.	$7:{\bigg (}{\frac {1}{4}}+{\frac {1}{28}}{\bigg )}S={\frac {1}{2}}\;\;\;;\;\;\;7B:{\bigg (}{\frac {1}{4}}+{\frac {1}{28}}{\bigg )}S={\frac {1}{2}}\;\;\;;\;\;\;8:{\frac {1}{4}}T={\frac {1}{2}}$ $9:{\bigg (}{\frac {1}{2}}+{\frac {1}{14}}{\bigg )}S=1\;\;\;;\;\;\;10:{\bigg (}{\frac {1}{4}}+{\frac {1}{28}}{\bigg )}S={\frac {1}{2}}\;\;\;;\;\;\;11:{\frac {1}{7}}S={\frac {1}{4}}$ $12:{\frac {1}{14}}S={\frac {1}{8}}\;\;\;;\;\;\;13:{\bigg (}{\frac {1}{16}}+{\frac {1}{112}}{\bigg )}S={\frac {1}{8}}\;\;\;;\;\;\;14:{\frac {1}{28}}S={\frac {1}{16}}$ $15:{\bigg (}{\frac {1}{32}}+{\frac {1}{224}}{\bigg )}S={\frac {1}{16}}\;\;\;;\;\;\;16:{\frac {1}{2}}T=1\;\;\;;\;\;\;17:{\frac {1}{3}}T={\frac {2}{3}}$ $18:{\frac {1}{6}}T={\frac {1}{3}}\;\;\;;\;\;\;19:{\frac {1}{12}}T={\frac {1}{6}}\;\;\;;\;\;\;20:{\frac {1}{24}}T={\frac {1}{12}}$	Les mêmes deux facteurs, (ici notés S et T) sont utilisés incessamment au travers de ces problèmes. Ahmès écrit effectivement le même problème différemment (7, 7B, 10), parfois en approchant le même problème avec un travail arithmétique différent.
21 à 38	Pour chacune des équations linéaires où la variable est $x$ , résolution de $x$ et expression de $x$ sous forme de développement égyptien	Soustractions $21:{\bigg (}{\frac {2}{3}}+{\frac {1}{15}}{\bigg )}+x=1\;\;\;\rightarrow \;\;\;x={\frac {1}{5}}+{\frac {1}{15}}$ $22:{\bigg (}{\frac {2}{3}}+{\frac {1}{30}}{\bigg )}+x=1\;\;\;\rightarrow \;\;\;x={\frac {1}{5}}+{\frac {1}{10}}$ $23:{\bigg (}{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{10}}+{\frac {1}{30}}+{\frac {1}{45}}{\bigg )}+x={\frac {2}{3}}\;\;\;\rightarrow \;\;\;x={\frac {1}{9}}+{\frac {1}{40}}$ Divisions simples $24:x+{\frac {1}{7}}x=19\;\;\;\rightarrow \;\;\;x=16+{\frac {1}{2}}+{\frac {1}{8}}$ $25:x+{\frac {1}{2}}x=16\;\;\;\rightarrow \;\;\;x=10+{\frac {2}{3}}$ $26:x+{\frac {1}{4}}x=15\;\;\;\rightarrow \;\;\;x=12$ $27:x+{\frac {1}{5}}x=21\;\;\;\rightarrow \;\;\;x=17+{\frac {1}{2}}$ Divisions en deux temps $28:{\bigg (}x+{\frac {2}{3}}x{\bigg )}-{\frac {1}{3}}{\bigg (}x+{\frac {2}{3}}x{\bigg )}=10\;\;\;\rightarrow \;\;\;x=9$ $29:{\frac {1}{3}}{\Bigg (}{\bigg (}x+{\frac {2}{3}}x{\bigg )}+{\frac {1}{3}}{\bigg (}x+{\frac {2}{3}}x{\bigg )}{\Bigg )}=10\;\;\;\rightarrow \;\;\;x=13+{\frac {1}{2}}$ Divisions plus complexes $30:{\bigg (}{\frac {2}{3}}+{\frac {1}{10}}{\bigg )}x=10\;\;\;\rightarrow \;\;\;x=13+{\frac {1}{23}}$ $31:x+{\frac {2}{3}}x+{\frac {1}{2}}x+{\frac {1}{7}}x=33\;\;\;\rightarrow$ $x=14+{\frac {1}{4}}+{\frac {1}{56}}+{\frac {1}{97}}+{\frac {1}{194}}+{\frac {1}{388}}+{\frac {1}{679}}+{\frac {1}{776}}$ $32:x+{\frac {1}{3}}x+{\frac {1}{4}}x=2\;\;\;\rightarrow \;\;\;x=1+{\frac {1}{6}}+{\frac {1}{12}}+{\frac {1}{114}}+{\frac {1}{228}}$ $33:x+{\frac {2}{3}}x+{\frac {1}{2}}x+{\frac {1}{7}}x=37\;\;\;\rightarrow \;\;\;x=16+{\frac {1}{56}}+{\frac {1}{679}}+{\frac {1}{776}}$ $34:x+{\frac {1}{2}}x+{\frac {1}{4}}x=10\;\;\;\rightarrow \;\;\;x=5+{\frac {1}{2}}+{\frac {1}{7}}+{\frac {1}{14}}$ Calcul d'inverse $35:{\bigg (}3+{\frac {1}{3}}{\bigg )}x=1\;\;\;\rightarrow \;\;\;x={\frac {1}{5}}+{\frac {1}{10}}$ $36:{\bigg (}3+{\frac {1}{3}}+{\frac {1}{5}}{\bigg )}x=1\;\;\;\rightarrow \;\;\;x={\frac {1}{4}}+{\frac {1}{53}}+{\frac {1}{106}}+{\frac {1}{212}}$ $37:{\bigg (}3+{\frac {1}{3}}+{\frac {1}{3}}\cdot {\frac {1}{3}}+{\frac {1}{9}}{\bigg )}x=1\;\;\;\rightarrow \;\;\;x={\frac {1}{4}}+{\frac {1}{32}}$ $38:{\bigg (}3+{\frac {1}{7}}{\bigg )}x=1\;\;\;\rightarrow \;\;\;x={\frac {1}{6}}+{\frac {1}{11}}+{\frac {1}{22}}+{\frac {1}{66}}$	Le problème 31 est doté d'une solution onéreuse. Alors que l'expression des problèmes 21-38 peut parfois apparaître compliquée (en particulier dans la prose d'Ahmès), chaque problème se réduit in fine à une simple équation linéaire. Dans certains cas, une unité de mesure égyptienne d'une certaine nature a été omise, étant superflue pour ces problèmes. Il s'agit des problèmes 35-38. Dans les déclarations et le travail apparaît la première mention d'unité de volume connue comme heqat et ro (où 1 heqat = 320 ro), qui seront importants dans le reste du papyrus. Pour le moment, cependant, leur mention littérale et leur utilisation en 35-38 reste cosmétique.
39	Cent pains vont être distribués parmi dix hommes de manière échelonnée. Cinquante pains vont être divisés également parmi quatre hommes de manière que chacun des quatre reçoive une portion égale $y$, pendant que les autres cinquante pains vont être divisés également parmi les six autres hommes de manière que chacun des six reçoive une part égale $x$. Trouver la différence entre ces deux parts $y-x$ et expression sous forme de développement égyptien.	$y-x=4+{\frac {1}{6}}$	Au problème 39, le papyrus commence à considérer les situations avec plus d'une seule variable. Il s'agit en fait d'un problème à une seule inconnue visant à calculer la différence entre cinquante quarts et cinquante sixièmes.
40	cent pains sont distribués parmi cinq hommes. Les parts de pain des hommes doivent être en suite arithmétique, de manière que des parts consécutives ne diffèrent que par une différence fixe, ou $\Delta$. De plus, la somme des trois portions la plus grande doit être égale à sept fois la somme des deux plus petites. Trouver $\Delta$ et écriture sous forme de développement égyptien.	$\Delta =9+{\frac {1}{6}}$	Le problème 40 achève la section arithmétique et/ou algébrique du papyrus, qui est suivie par une section géométrique. Après le problème 40, une grande section d'espace sur le papyrus matérialise la fin de la section. Comme pour le problème 40 lui-même, Ahmès travaille sa solution en considérant d'abord le cas analogue où le nombre de pains est de soixante et non plus cent. Il déclare alors que la différence est de 5 + 1/2 et que la plus petite part est égale à un, liste les autres, et alors développe/rééchelonne son travail pour revenir à cent pour produire son résultat. Bien qu'Ahmès n'exprime pas la solution en elle-même comme elle est décrite ici, la quantité est implicitement claire une fois rééchelonné son premier pas par la multiplication 5/3 x 11/2, pour lister les cinq portions (ce qu'il fait). Ce problème peut être considéré comme ayant quatre conditions : a) cinq parts se somment en cent, b) les parts vont de la plus petite à la plus grande, c) des parts consécutives ont une différence constante et d) la somme des trois parts les plus grandes est égale à sept fois la somme des deux plus petites. En commençant par les trois premières conditions seulement, l’algèbre élémentaire peut être utilisée avant de considérer s'il faut ajouter la quatrième condition pour conduire à un résultat consistant. Il apparaît qu'une fois les quatre solutions en place, la solution est unique. Le problème est alors un cas plus élaboré d'équation linéaire à résoudre que ce qui précède, se rapprochant ainsi de l'algèbre linéaire.
41	Utilisation de la formule de volume Un cylindre de rayon r et de hauteur h. $V={\bigg (}d-{\frac {1}{9}}d{\bigg )}^{2}h$ $={\frac {64}{81}}d^{2}h$ pour calculer le volume d'un silo à grain cylindrique dont le diamètre est de neuf coudées et la hauteur de dix coudées. Donner la réponse en termes de coudées cubiques. Puis, connaissant les conversions parmi les autres unités de volume, une coudée cubique = 3/2 khar = 30 heqats = 15/2 quadruple heqats, expression de la réponse en termes de khar et de quadruple heqats.	$V=640\;\;\;cubit^{3}$ $=960\;\;\;khar$ $=4800\;\;\;quadruple\;\;\;heqat$	Ce problème ouvre la section géométrique du papyrus, et donne aussi son premier résultat en fait incorrect (bien qu'avec une approximation de $\pi$ de bonne facture, l’approximation étant inférieure à 1 %). Les autres anciennes unités de volume égyptiennes telles que le quadruple heqat et le khar sont ensuite rapportées à ce problème via des conversions d'unité. Le problème 41 est donc aussi le premier problème à traiter substantiellement de l'analyse dimensionnelle.
42	Réutilisation de la formule et des unités de mesure données en 41 pour le calcul du volume d'un silo à grain cylindrique d'un diamètre de dix coudées et d'une hauteur de dix coudées. Donnant une réponse mesurée en coudées cubiques, le khar, et en centaines de quadruple heqats, où 400 heqats = 100 quadruple heqats = 1 centaine de quadruple heqat, tous sous forme de développement égyptien.	$V={\bigg (}790+{\frac {1}{18}}+{\frac {1}{27}}+{\frac {1}{54}}+{\frac {1}{81}}{\bigg )}\;\;\;cubit^{3}$ $={\bigg (}1185+{\frac {1}{6}}+{\frac {1}{54}}{\bigg )}\;\;\;khar$ $={\bigg (}59+{\frac {1}{4}}+{\frac {1}{108}}{\bigg )}\;\;\;hundred\;\;\;quadruple\;\;\;heqat$	Le problème 42 est effectivement une répétition du problème 41, conduisant à des conversions d'unité similaires à la fin. Cependant, bien que le problème commence comme expliqué, les calculs sont considérablement plus présents, et certains des derniers termes fractionnels ne sont en fait pas présents dans le document d'origine. Cependant, le contexte est suffisant pour comprendre le raisonnement, et Chace s'est donc permis d'ajouter certains termes fractionnels dans sa traduction mathématique (reprise ci-contre) ce qui donne une solution consistante du point de vue du lecteur contemporain.
43	Réutilisation de la formule de volume $V={\frac {2}{3}}{\Bigg (}{\bigg (}d-{\frac {1}{9}}d{\bigg )}+{\frac {1}{3}}{\bigg (}d-{\frac {1}{9}}d{\bigg )}{\Bigg )}^{2}h$ $={\frac {2048}{2187}}d^{2}h$ pour calculer le volume d'un silo à grain cylindrique d'un diamètre de neuf pour une hauteur de six coudées, avec résolution directe en développement égyptien de khar, et ensuite en développement égyptien de quadruple heqats et quadruple ro, où 1 quadruple heqat = 4 heqat = 1280 ro = 320 quadruple ro.	$V={\bigg (}455+{\frac {1}{9}}{\bigg )}\;\;\;khar$ $={\bigg (}2275+{\frac {1}{2}}+{\frac {1}{32}}+{\frac {1}{64}}{\bigg )}\;\;\;quadruple\;\;\;heqat$ $+{\bigg (}2+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{36}}{\bigg )}\;\;\;quadruple\;\;\;ro$	Le problème 43 contient la première erreur mathématique sérieuse du papyrus. Ahmès (ou bien la source depuis laquelle il l'a copié) a tenté un raccourci permettant de combiner en une seule opération le calcul de volume et la conversion d'unité depuis des coudées cubiques vers des khar en une seule étape, pour éviter d'avoir à utiliser des coudées cubiques en premier résultat. Cependant, cette tentative (qui échoue en raison d'une confusion entre les procédures du 41 et 42 et celui du 43, donne des résultats consistants par une méthode différente) au lieu du résultat dans une nouvelle formule de volume qui est inconsistante avec (et pire que) l'approximation utilisée en 41 et en 42.
44, 45	Une coudée cubique est égale à 15/2 quadruple heqats. Le point 44 considère un silo à grain cubique d'une longueur de 10 cubits sur chaque côté. Expression de son volume $V$ en termes de quadruples heqats. Le point 45 considère un silo à grain cubique d'un volume de 7500 quadruples heqats, et expression de sa longueur d'un côté $l$ en termes de cubits.	$V=7500$ quadruple heqat $l=10$ coudées	Le problème 45 est l'exact inverse du problème 44, et ils sont pour cela présentés ensemble ici.
46	Un silo à grains prismatique à section rectangulaire a un volume de 2500 quadruples heqats. Description de ces trois dimensions $l_{1},l_{2},l_{3}$ en unité coudées.	$l_{1}=l_{2}=10$ coudées $l_{3}=3+{\frac {1}{3}}$ coudées	Ce problème tel que formulé a bien sur une infinité de solutions, mais un choix simple proche lié aux problèmes 44 et 45 est fait.
47	Division de la quantité volumique physique de cent quadruples heqats par chacun des multiples de dix, depuis dix jusqu'à cent. Expression des résultats en développement égyptien en termes de quadruples heqats et de quadruple ro, et présentation des résultats dans une table.	${\begin{bmatrix}{\frac {100}{10}}&q.\;heqat&=&10&q.\;heqat\\{\frac {100}{20}}&q.\;heqat&=&5&q.\;heqat\\{\frac {100}{30}}&q.\;heqat&=&(3+{\frac {1}{4}}+{\frac {1}{16}}+{\frac {1}{64}})&q.\;heqat\\&&+&(1+{\frac {2}{3}})&q.\;ro\\{\frac {100}{40}}&q.\;heqat&=&(2+{\frac {1}{2}})&q.\;heqat\\{\frac {100}{50}}&q.\;heqat&=&2&q.\;heqat\\{\frac {100}{60}}&q.\;heqat&=&(1+{\frac {1}{2}}+{\frac {1}{8}}+{\frac {1}{32}})&q.\;heqat\\&&+&(3+{\frac {1}{3}})&q.\;ro\\{\frac {100}{70}}&q.\;heqat&=&(1+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{32}}+{\frac {1}{64}})&q.\;heqat\\&&+&(2+{\frac {1}{14}}+{\frac {1}{21}}+{\frac {1}{42}})&q.\;ro\\{\frac {100}{80}}&q.\;heqat&=&(1+{\frac {1}{4}})&q.\;heqat\\{\frac {100}{90}}&q.\;heqat&=&(1+{\frac {1}{16}}+{\frac {1}{32}}+{\frac {1}{64}})&q.\;heqat\\&&+&({\frac {1}{2}}+{\frac {1}{18}})&q.\;ro\\{\frac {100}{100}}&q.\;heqat&=&1&q.\;heqat\\\end{bmatrix}}$	Dans le problème 47, Ahmès est particulièrement insistant pour représenter le plus de chaînes élaborées de fractions comme Œil oudjat, autant qu'il le peut. À comparer aux problèmes 64 et 80 pour des préférences de représentation similaires. Par souci de brièveté, « quadruple » a été réduit à « q » dans tous les cas.
48	Comparaison de la superficie d'un disque de diamètre 9 à celle de son carré circonscrit, dont la taille d'un côté est également de 9. Ratio de la superficie du disque au carré?	${\frac {64}{81}}$	L'énoncé et la solution du problème 48 explicite clairement la méthode d'approximation de l'aire d'un disque, utilisé précédemment dans les problèmes 41-43. Cependant, elle ne vaut qu'une approximation de pi. L'énoncé original du problème 48 implique l’utilisation d'une unité de surface connue comme setat, auquel un contexte est ajouté dans les problèmes suivants.
49	Le khet est une unité de longueur, égale à cent coudées. Aussi un cubit strip est une mesure d'aire rectangulaire, correspondant à un rectangle d'une coudée par cent coudées, ou cent coudées carrés. Considérer un terrain rectangulaire de dix khet par un khet. Expression de sa surface $A$ en termes de cubit strips.	$A=1000\;\;\;cubit\;\;\;strip$	-
50	Un khet carré est une unité de longueur égale à un setat. Considérer un disque d'un diamètre de neuf khet. Expression de sa superficie $A$ en termes de setat.	$A=64\;\;\;setat$	Le problème 50 est en fait l'application simple de la formule de calcul de la superficie d'un cercle basée sur le ratio 64/81 énoncé au problème 48.
51	Une parcelle triangulaire d'une base de quatre khet et d'une hauteur de dix. Trouver son aire $A$ en setat .	$A=20\;\;\;setat$	L’énoncé et la solution du 51 rappellent la formule familière pour le calcul de l'aire d'un triangle, et pour Chace elle est paraphrasée comme telle. Cependant, le diagramme triangulaire du papyrus, erreur précédente, et les problématiques de traduction présentent des ambiguïtés sur le fait que le triangle puisse être un triangle à angle droit ou si Ahmès en fait comprend les conditions lesquelles la réponse énoncée est correcte. Spécifiquement, la dimension de dix khet signifie-t-elle une hauteur (auquel cas le problème est bien formulé) ou bien « dix khet » se réfère-t-il simplement à un côté du triangle, auquel cas la figure devrait être un triangle rectangle. Ces problématiques et confusions se poursuivent à travers les problèmes 51-53, au point qu'Ahmès peut donner le sentiment de perdre la compréhension de ce qu'il fait, spécialement au 53.
52	Une parcelle trapézoïdale a deux bases, de six khet et quatre khet. Sa hauteur est de vingt khet. Trouver sa surface $A$ en setat .	$A=100\;\;\;setat$	Les considérations du problème 52 sont très similaires à celles du 51. La méthode de résolution est familière des méthodes modernes, et donc les circonstances comme celles du 51 lèvent le doute sur la manière dont Ahmes ou sa source comprenaient ce qu'ils faisaient.
53	Un triangle isocèle (une étendue de terre, par exemple) a une base égale à 4 1/2 khet et une altitude égale à 14 khet. Deux segments de ligne parallèles à la base divisent davantage le triangle en trois secteurs, à savoir un trapèze inférieur, un trapèze central et un triangle supérieur (similaire) plus petit. Les segments de droite coupent la hauteur du triangle en son milieu (7) et plus loin à un quart de point (3 1/2) plus près de la base, de sorte que chaque trapèze a une hauteur de 3 1/2 khet, tandis que le plus petit triangle similaire a une hauteur de 7 khet. Trouvez les longueurs $l_{1},l_{2}$ des deux segments de ligne, où ils sont respectivement les segments de ligne les plus courts et les plus longs, et exprimez-les en termes fractionnaires égyptiens de khet. De plus, trouvez les aires $A_{1},A_{2},A_{3}$ des trois secteurs, où ils sont respectivement le grand trapèze, le trapèze du milieu et le petit triangle, et exprimez les en termes fractionnaires égyptiens de cubit strip et de coudées. Utilisez le fait que 1 setat = 100 cubit strip pour les conversions d'unités.	$l_{1}={\bigg (}2+{\frac {1}{4}}{\bigg )}\;\;\;khet$ $l_{2}={\bigg (}3+{\frac {1}{4}}+{\frac {1}{8}}{\bigg )}\;\;\;khet$ $A_{1}={\bigg (}13+{\frac {1}{2}}+{\frac {1}{4}}{\bigg )}\;\;\;setat+{\bigg (}3+{\frac {1}{8}}{\bigg )}\;\;\;cubit\;\;\;strip$ $A_{2}={\bigg (}9+{\frac {1}{2}}+{\frac {1}{4}}{\bigg )}\;\;\;setat+{\bigg (}9+{\frac {1}{4}}+{\frac {1}{8}}{\bigg )}\;\;\;cubit\;\;\;strip$ $A_{3}={\bigg (}7+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}{\bigg )}\;\;\;setat$	Le problème 53, étant plus complexe, se heurte à bon nombre des mêmes problèmes que les problèmes 51 et 52 : des ambiguïtés de traduction et plusieurs erreurs numériques. En particulier concernant le grand trapèze inférieur, Ahmès semble s'entêter à trouver la base supérieure, et propose dans l'ouvrage original de soustraire « un dixième, égal à 1 + 1/4 + 1/8 setat plus 10 cubit strip » d'un le rectangle étant (vraisemblablement) 4 1/2 x 3 1/2 (khet). Cependant, même la réponse d'Ahmès ici est incompatible avec les autres informations sur le problème. Heureusement, le contexte de 51 et 52, ainsi que la base, la ligne médiane et l'aire du triangle plus petit (qui « sont » donnés comme 4 + 1/2, 2 + 1/4 et 7 + 1/2 + 1/ 4 + 1/8, respectivement) permettent d'interpréter le problème et sa solution comme cela a été fait ici. La paraphrase donnée représente donc une meilleure hypothèse cohérente quant à l’intention du problème, qui suit Chace. Ahmès fait également référence aux « cubit strip » au cours du calcul de ce problème, et nous répétons donc leur utilisation ici. Il convient de mentionner que ni Ahmès ni Chace ne donnent explicitement l'aire du trapèze moyen dans leurs traitements (Chace suggère que c'est une trivialité du point de vue d'Ahmès) ; la liberté a donc été prise de le signaler d'une manière qui est cohérente avec ce que Chace avait avancé jusqu'à présent.
54	Il y a 10 parcelles de terrain. Dans chaque parcelle, un secteur est cloisonné de telle sorte que la somme des superficies de ces 10 nouvelles cloisons soit de 7 setat. Chaque nouvelle partition a une superficie égale. Trouvez l'aire $A$ de l'une de ces 10 nouvelles partitions et exprimez-la en termes fractionnaires égyptiens de setats et de cubit strip.	$A={\bigg (}{\frac {1}{2}}+{\frac {1}{5}}{\bigg )}\;\;\;setat$ $={\bigg (}{\frac {1}{2}}+{\frac {1}{8}}{\bigg )}\;\;\;setat+{\bigg (}7+{\frac {1}{2}}{\bigg )}\;\;\;cubit\;\;\;strip$	-
55	Il y a 5 parcelles de terrain. Dans chaque parcelle, un secteur est cloisonné de telle sorte que la somme des superficies de ces 5 nouvelles cloisons soit de 3 setat. Chaque nouvelle partition a une superficie égale. Trouvez l'aire $A$ de l'une de ces 5 nouvelles partitions et exprimez-la en termes fractionnaires égyptiens de setats et de cubit strip.	$A={\bigg (}{\frac {1}{2}}+{\frac {1}{10}}{\bigg )}\;\;\;setat$ $={\frac {1}{2}}\;\;\;setat+10\;\;\;cubit\;\;\;strip$	-
56	1) L'unité de longueur connue sous le nom de coudée royale est (et a été, tout au long du papyrus) ce que l'on entend lorsque nous faisons simplement référence à une « coudée ». Une coudée « royale », ou une coudée, est égale à sept paumes, et une paume est égale à quatre doigts. En d'autres termes, les égalités suivantes sont vraies : 1 coudée (royale) = 1 coudée = 7 paumes = 28 doigts. 2) Considérons un pyramide à base carrée dont la base, la face carrée est coplanaire avec un plan (ou le sol, disons), de sorte que l'un des plans contenant ses faces triangulaires a l'angle dièdre de $\theta$ par rapport au plan de masse (c'est-à-dire à l'intérieur de la pyramide). En d'autres termes, $\theta$ est l'angle des faces triangulaires de la pyramide par rapport au sol. Le seked d'une telle pyramide, ayant alors une hauteur $a$ et une longueur de bord de base $b$ , est défini comme « cette longueur physique » $S$ tel que ${\frac {S}{1\;\;\;royal\;\;\;cubit}}=$ $\cot {\theta }$. En d'autres termes, le seked d'une pyramide peut être interprété comme le rapport de ses faces triangulaires « par une unité (coudée) d'élévation ». Ou, pour le triangle rectangle approprié à l'intérieur d'une pyramide ayant des branches $a,{\frac {b}{2}}$ et la médiatrice perpendiculaire d'une face triangulaire comme hypoténuse, alors la pyramide seked $S$ satisfait $\cot {\theta }={\frac {b}{2a}}={\frac {S}{1\;\;\;royal\;\;\;cubit}}$. Des triangles similaires sont donc décrits, et l’un peut être mis à l’échelle de l’autre. 3) Une pyramide a une altitude de 250 coudées (royales) et le côté de sa base a une longueur de 360 coudées (royales). Trouvez son seked $S$ en termes fractionnaires égyptiens de coudées (royales), ainsi qu'en termes de paumes.	$S={\bigg (}{\frac {1}{2}}+{\frac {1}{5}}+{\frac {1}{50}}{\bigg )}\;\;\;cubit$ $={\bigg (}5+{\frac {1}{25}}{\bigg )}\;\;\;palm$	Le problème 56 est le premier des « problèmes de pyramide » ou problèmes de seked du papyrus Rhind, 56-59, 59B et 60, qui concernent la notion d'inclinaison faciale d'une pyramide par rapport à un terrain plat. À cet égard, le concept de seked suggère les débuts de la trigonométrie. Cependant, contrairement à la trigonométrie moderne, notez en particulier qu'un seked se trouve par rapport à une pyramide et est lui-même une « mesure de longueur physique », qui peut être donnée en termes de n'importe quelle unité physique de longueur. Cependant, pour des raisons évidentes, nous (et le papyrus) limitons notre attention aux situations impliquant des unités égyptiennes anciennes. Les coudées royales sont utilisées dans tout le papyrus, pour les différencier des coudées « courtes » qui étaient utilisées ailleurs dans l'Égypte ancienne. Une coudée « courte » équivaut à six paumes.
57, 58	Le seked d'une pyramide est composée de 5 paumes et d'un doigt, et le côté de sa base est de 140 coudées. Trouvez (57) sa hauteur $a$ en termes de coudées. De plus (58), la hauteur d'une pyramide est de 93 coudées + 1/3, et le côté de sa base est de 140 coudées. Trouvez son seked $S$ et exprimez-le en termes de paumes et de doigts.	$a={\bigg (}93+{\frac {1}{3}}{\bigg )}\;\;\;cubit$ $S=5\;\;\;palm+1\;\;\;finger$	Le problème 58 est l'inverse du problème 57, et ils sont donc présentés ensemble ici.
59, 59B	La hauteur d'une pyramide (59) est de 8 coudées et la longueur de sa base est de 12 coudées. Exprimez son seked $S$ en termes de paumes et de doigts. De plus (59B), le seked d'une pyramide est de cinq paumes et d'un doigt, et le côté de sa base est de 12 coudées. Exprimez son altitude $a$ en termes de coudées.	$S=5\;\;\;palm+1\;\;\;finger$ $a=8\;\;\;cubit$	Les problèmes 59 et 59B considèrent un cas similaire à 57 et 58, se terminant par des résultats familiers.
60	Si un pilier (c'est-à-dire un cône) a une hauteur de 30 coudées et que le côté de sa base (ou diamètre) a une longueur de 15 coudées, trouvez son seked $S$ et exprimez-le en termes de coudées.	$S={\frac {1}{4}}\;\;\;cubit$	Ahmès utilise des mots légèrement différents pour présenter ce problème, qui se prêtent à des problèmes de traduction. Cependant, le contexte général du problème, ainsi que le diagramme qui l'accompagne (qui diffère des diagrammes précédents), amènent Chace à conclure qu'il s'agit d'un cône. La notion de seked se généralise facilement à la face latérale d'un cône ; il rapporte donc le problème en ces termes. Le problème 60 conclut la section géométrique du papyrus. De plus, c'est le dernier problème sur le recto du document ; tout le contenu ultérieur de ce résumé est présenté au verso du papyrus. Le passage de 60 à 61 ans est donc à la fois un déplacement thématique et physique dans le papyrus.

Voir aussi

Bibliographie

• (en) Ernest Alfred Wallis Budge, Facsimilé of the Rhind mathematical papyrus in the British Museum, British Museum, 1898 (lire en ligne).
• David M. Burton, History of Mathematics : An Introduction, Boston, Wm. C. Brown, 2003
• (en) Arnold Buffum Chace, Henry Parker Manning et Raymond Clare Archibald, The Rhind Mathematical Papyrus : Free Translation and Commentary, vol. I, Mathematical Association of America, 1927 (lire en ligne).
• (en) Arnold Buffum Chace, Ludlow Bull et Henry Parker Manning, The Rhind Mathematical Papyrus : Photographs, Transcription Transliteration, Literal Translation, vol. II, Mathematical Association of America, 1929 (lire en ligne).
• (en) Marshall Clagett, Ancient Egyptian Science, A Source Book. Volume Three : Ancient Egyptian Mathematics, American Philosophical Society, coll. « Memoirs of the American Philosophical Society », 1999, 462 p. (ISBN 978-0-87169-232-0, lire en ligne).
• Sylvia Couchoud, Mathématiques égyptiennes : Recherches sur les connaissances mathématiques de l'Égypte pharaonique, Le Léopard d’Or, 1993, 208 p. (ISBN 2-86377-118-3).
• (de) August Eisenlohr, Ein mathematisches Handbuch der alten Ägypter (Papyrus Rhind des British Museum), übersetzt und erklärt, Leipzig, J. C. Hinrichs, 1877 (lire en ligne).
• Jérôme Gavin et Alain Schärlig, « Fausse position et heuristique au Moyen Empire », ENiM, vol. 8,‎ 2015, p. 113-132 (lire en ligne).
• (en) Richard J. Gillings, Mathematics in the Time of the Pharaohs, Boston, MIT Press, 1972, 286 p. (ISBN 0-262-07045-6).
• Michel Guillemot, « Calcul et géométrie dans l’Égypte ancienne », dans Histoire du calcul de la géométrie à l'algèbre, sous la direction de Luc Sinègre, Paris, Vuibert, 2009 (ISBN 978-2-7117-2226-6).
• (de) Annette Imhausen, Ägyptische Algorithmen : Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten, Wiesbaden, Harrassowitz, 2003, 387 p. (ISBN 3-447-04644-9, lire en ligne).
• (en) Annette Imhausen, « Egyptian Mathematics », dans Victor J. Katz, The Mathematics of Egypt, Mesopotamia, China, India, and Islam : A Sourcebook, Princeton, Princeton University Press, 2007 (ISBN 0-691-11485-4), p. 7-56.
• (en) Annette Imhausen, Mathematics in Ancient Egypt: A Contextual History, Princeton University Press, 2016 (ISBN 9780691209074, lire en ligne).
• Marianne Michel, Les mathématiques de l'Égypte ancienne. Numération, métrologie, arithmétique, géométrie et autres problèmes, Bruxelles, Safran (éditions), 2023, 604 p. [détail des éditions].
• (en) Thomas Eric Peet, The Rhind mathematical papyrus : British Museum 10057 and 10058 ; Introduction, transcription, translation and commentary, Liverpool, The University press of Liverpool, 1923, 135 p. (lire en ligne) et 25 planches (éd. moderne du Papyrus Rhind)
• (en) Gay Robins et Charles Shute, The Rhind Mathematical Papyrus : an ancient Egyptian text, Londres, British Museum, 1987, 60 p. (ISBN 0-486-26407-6).
• (en) Corinna Rossi, Architecture and Mathematics in Ancient Egypt, Cambridge University Press, 2007 (1^re éd. 2003), 280 p. (ISBN 978-0-521-69053-9).
• (en) Anthony Spalinger, « The Rhind Mathematical Papyrus as a Historical Document », Studien zur Altägyptischen Kultur, Helmut Buske Verlag GmbH, vol. 17,‎ 1990, p. 295-337.
• (en) Antony J. Spalinger, War in Ancient Egypt : The New Kingdom, Blackwell Publishing, 2005, 312 p. (ISBN 1-4051-1372-3).

Articles connexes

• Mathématiques dans l'Égypte antique
• Papyrus de Moscou
• Papyrus d'El-Lahoun
• Papyrus de Berlin
• Rouleau de cuir des mathématiques égyptiennes
• Tablettes de bois du Caire (en)

Liens externes

• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Britannica
  • Gran Enciclopèdia Catalana
• Notices d'autorité :

  • GND
• (en) Le papyrus Rhind, sur le site du British Museum : BM 10058 et BM 10057
• (en) « Collections: Egyptian, Classical, Ancient Near Eastern Art: Fragments of Rhind Mathematical Papyrus », Brooklyn Museum (consulté le 25 novembre 2013)
• Michel Guillemot et Daniel Austin, « Papyrus Rhind : Edition commentée du Papyrus Rhind »