Prisme (optique)

Un prisme est un bloc de verre taillé, composé classiquement de trois faces sur une base triangulaire, mais qui peut adopter des formes plus complexes et éloignées du prisme à base triangulaire usuel. C'est un instrument optique utilisé pour réfracter la lumière, la réfléchir ou la disperser. Des prismes spéciaux peuvent aussi servir à diffracter la lumière, la polariser ou en séparer les polarisations ou encore créer des interférences.
Utilisé dans l'Antiquité pour son côté décoratif, sous forme de perles ou pour décomposer la lumière, le prisme connaît son premier essor comme instrument scientifique durant le Moyen Âge tardif. Il a permis de grandes avancées dans la compréhension de la composition de la lumière grâce aux expériences d'Isaac Newton au XVIIIe siècle. Depuis, les prismes ont été utilisés majoritairement en spectroscopie et dans toute application nécessitant des déviations ou des séparations de faisceau. Considéré comme un outil rudimentaire depuis son âge d'or en spectroscopie, les prismes demeurent omniprésents en optique dans de multiples applications comme la séparation d'harmonique.
Histoire
[modifier | modifier le code]
Appelés vitrum trigonum du temps de la Rome antique[1], un récit de Pline l'Ancien en mentionnerait l'existence dans un passage traitant d'un cristal taillé en prisme capable de transformer la lumière du soleil en arc-en-ciel[2]. La manufacture à cette époque de perles de verre de forme prismatique a été attestée en particulier sur le site de Ban Don Ta Phet (thaï : บ้านดอนตาเพชร), un site archéologique de l'âge du fer dans l'Amphoe Phanom Thuan en Thaïlande. Ces perles, transparentes ou translucides, sont volontairement taillées en forme de prismes similaires aux cristaux naturels à base triangulaire ou hexagonale par exemple[3],[4]. L'existence de prismes ou d'éléments similaires est aussi attestée par Sénèque qui mentionne dans ses Questiones naturæ des baguettes de verre qui servent à transformer la lumière en un arc-en-ciel[5],[6],[7], prismes qui auraient été très utilisés de son temps. Sénèque attribue cependant à cette époque les couleurs de l'arc-en-ciel à des fausses couleurs fugitives comme les reflets irisés des plumes de pigeon[8]. En 1275, Vitellion reproduit ce phénomène en remplissant un prisme de base hexagonale avec de l'eau ; en faisant passer de la lumière au travers, la lumière est décomposée[9].

Si le prisme est connu depuis longtemps, la « transformation » de la lumière du soleil en de multiples couleurs n'est toujours pas expliquée et les couleurs sont considérées jusqu'au XVIIe siècle comme des mélanges d'ombre et de lumière[10],[11] ou comme le mélange de particules de la surface des objets avec des particules de lumière[10]. Il faut attendre les expériences d'Isaac Newton, qui cherche à comprendre la déformation du faisceau en sortie du prisme plutôt que de s'intéresser aux couleurs, pour que la décomposition du spectre soit comprise. Le faisceau, ovale, est déformé, ce qui se heurte aux lois de la réfraction alors connues : l'indice de réfraction était considéré comme unique et propre au milieu qui modifiait la lumière. Newton montre par ses expériences que ce n'est pas le prisme qui modifie la lumière mais les propriétés du matériau qui sont différentes pour les couleurs[11].
L'utilisation croissante des prismes est concomitante avec la découverte du phénomène de dispersion de la lumière blanche et la compréhension que celle-ci est composée d'un continuum de couleurs[12]. C'est aussi grâce à cette expérience des prismes que l'on a compris le caractère inévitable des aberrations chromatiques dans les télescopes[13]. À partir du début du XIXe siècle, les recherches sur l'éther deviennent de plus en plus nombreuses, et les expériences visant à en démontrer l'existence se multiplient. En 1810, François Arago cherche à observer la différence de vitesse des ondes lumineuses dans l'éther grâce à la déviation des rayons stellaires dans un prisme à différentes heures du jour. Cette expérience est réinterprétée par Augustin Fresnel qui en déduit que l'éther subit un entraînement partiel dans les milieux réfringents comme celui du prisme[14]. Un siècle de recherches s'acheve en tous les cas par l'abandon de la théorie de l'éther.
Réalisation des prismes
[modifier | modifier le code]Les prismes utilisés en optique, du fait de leur emploi dans des applications de précision, sont des blocs de matériau transparent, homogène et isotrope. Cela implique une qualité de verre très importante. Certains prismes, les prismes à liquide, sont des parois formant un angle dans lequel est coulé un liquide comme de l'eau.
Il existe peu de machines pour l'usinage à la chaîne de prismes optiques de précision du fait de la grande variété de forme, de taille et de qualité des prismes. Leur utilisation finale détermine la précision avec laquelle ils sont usinés[L 1]. On retrouve parmi les fabricants de composants optiques des précisions allant de l'arcminute à l'arcseconde pour l'angle au sommet, et des qualités de polissage jusqu'à 20/10 en scratch and dig ce qui représente la qualité usuellement requise dans les applications à laser pulsé[L 2].
Le processus d'usinage est similaire à celui d'autres composants en verre optique comme les lentilles : une étape d'ébauchage est effectuée sur le bloc de verre, puis un rodage plus fin avant polissage jusqu'à atteindre la qualité optique désirée. À chaque étape, l'angle est contrôlé à la main. La fabrication d'un prisme est assez longue et les prismes les plus complexes, à surfaces nombreuses, comme les prismes en toit, ne font qu'allonger la durée de l'usinage et multiplier les contrôles optiques nécessaires[L 1].
Après ces trois étapes, les arêtes non utilisées de certains prismes peuvent être chanfreinées. Ensuite, le prisme est soumis à un traitement anti-reflet si besoin[L 1],[L 2].
Géométrie
[modifier | modifier le code]Un prisme en optique est défini par son « angle d'ouverture » : un prisme à 30° possède un angle au sommet tel. Ce sommet est l'arête principale du prisme, qui est formée par l'intersection de deux des faces du prisme. Dans un prisme à base triangulaire, la troisième face est nommée « base » et n'intervient que dans le cas des prismes à réflexion totale[15].
Prismes en toit
[modifier | modifier le code]Les prismes en toit sont des prismes dont une des faces n'est plus plane mais taillée en « toit », c'est-à-dire en un coin à angle droit. Ils peuvent servir à inverser l'image formée par le prisme[16], cette nouvelle arête étant orientée selon l'axe de symétrie désiré pour l'inversion de l'image[17].
Pentaprisme
[modifier | modifier le code]
Le pentaprisme est un prisme complexe. Il est principalement utilisé en photographie dans les appareils reflex à viseur optique pour retourner l'image avant de la transmettre dans le viseur optique. Le premier constructeur à l'avoir utilisé en 1957 est Pentax[18].
Association de prismes
[modifier | modifier le code]
Les prismes optiques peuvent être utilisés par paire, séparés spatialement ou accolés que ce soit par une colle ou par contact optique[L 3].
Utilisations
[modifier | modifier le code]Déflexion de faisceau
[modifier | modifier le code]Les prismes à réflexion totale sont utilisés pour dévier la lumière sans perte dans des systèmes optiques comme les jumelles ou les appareils photographiques ; ils sont une alternative aux miroirs[19],[20]. Un prisme rétroréflecteur possède ainsi un intérêt majeur par rapport aux miroirs, étant donné que, quelle que soit l'orientation du prisme, le faisceau sera renvoyé dans le sens inverse du faisceau incident, parallèlement tant que les faces du prisme forment bien un angle de 90° entre elles : ce système est plus facile à aligner qu'un système à miroirs où l'angle d'incidence du faisceau a une importance bien plus grande[L 3]. Les prismes « coin de cube » présentent aussi cette particularité dans les trois dimensions.
Anamorphose de faisceau
[modifier | modifier le code]La configuration géométrique d'un prisme fait qu'une anamorphose de faisceau est possible ; souvent réalisée à l'aide d'une paire de prismes, on retrouve cette utilisation de manière fréquente pour la symétrisation des faisceaux des lasers[L 3].
Le principe repose sur de l'optique géométrique simple. Un seul prisme est nécessaire pour réaliser une anamorphose mais le faisceau sera dévié. Une paire de prismes permet de conserver la direction de la lumière tout en réalisant l'anamorphose. Pour une meilleure transmission, on réalise le plus souvent ce montage avec un angle d'incidence proche ou à angle droit et une sortie de prisme à l'angle de Brewster de manière que la polarisation TM du faisceau soit totalement transmise. Dans le cas simple à un seul prisme, l'anamorphose — le rapport des rayons du faisceau sortant sur le faisceau entrant — sera, selon l'orientation du prisme, d'un facteur égal à l'indice de réfraction du prisme ou à l'inverse de l'indice[L 4].
Lorsque l'on utilise une paire de prismes identiques pour réaliser l'anamorphose, le facteur s'élève à l'indice au carré, ou son inverse au carré. Il demeurera aussi un offset du faisceau sortant qui, bien que parallèle au faisceau d'entrée, aura été décalé par les réfractions des prismes. Pour annuler l'offset, le montage devrait contenir alors quatre prismes en tout[L 4].
Une des principales limitations de ce montage est sa sensibilité à la longueur d'onde : puisque l'on travaille en transmission, il n'est pas possible de se départir de la dispersion chromatique. Par ailleurs, les diodes lasers, qui émettent des faisceaux astigmatiques, ne peuvent être anamorphosées par ces systèmes puisque les prismes ne peuvent focaliser les waists décalés du faisceau[L 4].
Prismes dispersifs
[modifier | modifier le code]Les prismes dispersifs ont été très employés en spectroscopie dans des instruments appelés spectroscopes à prismes et dans les spectrophotomètres à prisme[21]. Le premier spectroscope à prismes a été inventé vers 1860 par Gustav Kirchhoff et Robert Bunsen[22]. Bien que les prismes soient encore très utilisés dans ce domaine, les réseaux de diffraction les ont progressivement remplacés, à la fois pour des raisons économiques et pour leur plus grand pouvoir de résolution[23].
Outre cette utilisation, les prismes dispersifs sont aussi employés avec les lasers, afin d'épurer un faisceau ayant subi un doublage de fréquence par exemple, ou bien pour recombiner deux faisceaux de longueurs d'onde différentes. La dispersion créée par un prisme peut permettre, lorsqu'il est inséré dans une cavité laser, de régler finement la longueur d'onde d'émission[L 3].
Dans le cas des lasers à blocage de mode (en anglais mode-locking), deux prismes dispersifs appairés permettent de contrôler la dispersion en fréquence grâce au fait que le chemin optique devient dépendant de la longueur d'onde[L 3]. La dispersion introduite peut devenir anormale mais les pertes sont limitées dès lors que les faisceaux sont incidents à l'angle de Brewster[L 5].
Le premier prisme va simplement disperser la lumière selon les longueurs d'onde, et le deuxième prisme, tête-bêche par rapport au premier, réfracte le faisceau parallèlement au faisceau d'entrée, mais chaque longueur d'onde va sortir en un point différent de la face de sortie du deuxième prisme, ces points étant dépendants de la longueur d'onde : on parle dans ce cas de « chirp spatial »[L 5].
Correction des amétropies
[modifier | modifier le code]En ophtalmologie, les prismes sont utilisés lorsqu'il est nécessaire de corriger un strabisme[24]. On appelle « corrections prismatiques » les corrections du strabisme utilisant un prisme. Il est possible de sur-corriger (hypercorrection prismatique) ou de sous-corriger (hypocorrection prismatique) ce strabisme pour différentes raisons : activation de zones rétiniennes non utilisées, acclimatation progressive à la correction totale ultérieure, etc.[25],[26].
Polarisation
[modifier | modifier le code]Il est parfois utile de séparer les polarisations ou de filtrer les polarisations d'un faisceau de lumière. Pour ce faire, parmi les multiples polariseurs possibles existent des montages à prisme. Composé de matériaux biréfringents, le montage le plus classique comprend deux prismes, dont les axes de polarisation de la lumière sont orientés différemment, joints par la grande face, et formant ainsi un cube[L 6].
Ces cubes séparateurs ont l'avantage de pouvoir supporter de grandes puissances puisque leur usage consiste à séparer un faisceau et non d'en absorber une partie.
Les prismes polariseurs sont encore très utilisés bien que concurrencés par d'autres dispositifs polarisants. Très pratiques dans l'ultraviolet mais limités par les propriétés de la matière dont ils sont faits et/ou de la colle qui joint les deux prismes, on retrouve des prismes polariseurs de type Rochon ou Wollaston pour des applications du proche UV au VUV, avec des prismes taillés dans de la calcite ou du fluorure de magnésium[27].
Propriétés d'un prisme à base triangulaire
[modifier | modifier le code]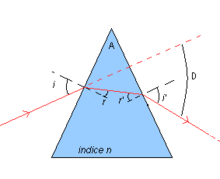
Dans le cadre des sections suivantes, plusieurs calculs sont développés avec les annotations suivantes :
- i l'angle d'incidence sur le prisme ;
- i' l'angle d'émergence du prisme ;
- r l'angle de la 1re réfraction ;
- r' l'angle de la 2e réfraction ;
- A l'angle au sommet du prisme ;
- D l'angle de déviation entre le rayon émergent et le rayon incident ;
- n l'indice normalisé du matériau du prisme.
Stigmatisme
[modifier | modifier le code]Le stigmatisme rigoureux d'un prisme n'a lieu que dans deux cas[28] :
- Pour les points appartenant aux arêtes, un cas trivial sans intérêt ;
- Pour les points situés à l'infini.
Conditions d'émergence
[modifier | modifier le code]Du fait du phénomène de réflexion totale, selon la configuration géométrique du système et l'angle d'incidence, il est possible que le rayon ne puisse pas émerger. Les conditions d'émergence sont des conditions nécessaires et suffisantes pour qu'il existe un faisceau sortant. Pour le faisceau d'entrée, et pour le faisceau de sortie, [29].
Ceci implique d'abord pour l'angle au sommet du prisme que où le cas limite implique que , le reste ne pouvant être une condition suffisante à l'émergence d'un faisceau, certains rayons pouvant être réfractés vers la seconde face et d'autres totalement réfléchis[29].
Cela implique aussi pour l'angle d'incidence que [29].
Déviation
[modifier | modifier le code]
Suivant les lois de Snell-Descartes, au premier dioptre et au deuxième dioptre. Étant donné que la somme des angles d'un triangle est égale à pi, on trouve et [30].
Si les angles sont très petits, il est possible, par développement limité des fonctions trigonométriques, de simplifier les sinus par l'angle permettant d'aboutir à [30].
Les angles d'incidence étant rarement suffisamment faibles pour se placer dans le cadre de cette approximation, on trouve :

L'angle de déviation ainsi trouvé possède un minimum, que l'on peut trouver au point où la dérivée de la déviation en fonction de l'incidence s'annule. On peut retrouver ceci en dérivant les expressions par rapport à i[31] :
Et comme le minimum de déviation se trouverait à l'angle auquel la dérivée de la déviation s'annule, il vient :
simplifiable en :
Les matériaux utilisés pour les prismes optiques ont des indices supérieurs à 1, ce qui signifie que le terme nul satisfaisant la précédente formule est . Les sinus des angles d'incidence et d'émergence sont égaux, donc les sinus des deux angles de réfraction le sont aussi. De ce fait, au minimum de déviation, [31]
Dispersion
[modifier | modifier le code]


Le phénomène de dispersion qui a donné ses lettres de noblesse au prisme est particulièrement lié à l'indice du verre utilisé. L'indice de réfraction d'un matériau est dépendant de la longueur d'onde de la lumière. La déviation n'est donc pas la même pour chaque longueur d'onde, ce qu'il est possible de montrer par la différenciation des formules du prisme[32] :
Il vient alors : , que l'on peut simplifier en : . Cette expression montre que la déviation est une fonction croissante de l'indice. Or d'après Cauchy, donc l'indice est une fonction décroissante de la longueur d'onde ; en conséquence, ce sont les grandes longueurs d'onde (rouge) qui ont l'indice le plus petit, et donc qui sont le moins déviées, contrairement aux réseaux de diffraction dont la déviation des longueurs d'onde se fait dans le sens inverse : les plus grandes étant plus déviées[32].
Matériaux de fabrication
[modifier | modifier le code]Au début de l'utilisation massive des prismes comme instruments de spectrométrie, les matériaux utilisés étaient majoritairement des cristaux naturels comme le quartz cristallin, la fluorine et le cristal de sel, et notamment les prismes pour l'infrarouge moyen sont jusque dans les années 1940 taillés dans des cristaux, malgré les difficultés pour en trouver d'une pureté suffisante : les réseaux de diffraction étaient alors plus chers encore que les prismes[33].
Cet avantage financier des prismes sur les réseaux s'atténue après la Seconde Guerre mondiale : des cristaux synthétiques permettent de diminuer le coût de production des prismes mais des méthodes de réplication des réseaux sont découvertes de manière concomitante[33].
Dans le cas de prismes dispersifs, le matériau est essentiellement conditionné par la bande spectrale d'intérêt et la résolution que peut atteindre le prisme[34].
| Matière | Bande spectrale (µm) | Lieu de meilleure résolution spectrale (µm) | |
|---|---|---|---|
| Nom | Formule chimique | ||
| Fluorure de lithium | LiF | 2—5,3 ou 0,120—9 µm[27] | 4,3 |
| Fluorine | CaF2 | 5,3—8,5 ou 0,13—12 µm[27] | 8,3 |
| Chlorure de sodium | NaCl | 8,5—15,4 ou 0,2—26 µm[27] | 11,1 |
| Bromure de potassium | KBr | 15,4—26 ou 0,25—40 µm[27] | 20 |
| Bromure de césium | CsBr | 14—38 ou 0,3—55 µm[27] | 28,6 |
| Iodure de césium | CsI | 20—50 ou 0,25—80 µm[27] | 40 |
| Nom | Formule chimique | Usage |
|---|---|---|
| Quartz | SiO2 | |
| Calcite | CaCO3 | La calcite est idéalement adaptée au dispositif Glan-Taylor[35] et fait partie des matériaux utilisés depuis le plus longtemps pour les prismes polariseurs, notamment celui de Nicol et les autres prismes de type Glan[36]. |
| Orthovanadate d'yttrium | YVO4 | L'orthovanadate comme le vanadate d'yttrium sont utilisés pour des prismes de Rochon, de Wollaston et de Glan, le plus adapté étant le Glan-Taylor[35]. Sa transmission très bonne de 3 à 5 µm en font un matériau adapté au NIR. |
| Bêta-borate de baryum (BBO) | β-BaB2O4 | |
| Fluorure de magnésium | MgF2 | Utilisé en VUV[37], notamment dans des dispositifs Rochon[38] ou Wollaston[39]. |
Notes et références
[modifier | modifier le code]- Goury 1833, p. 357.
- Jomard 1818, p. 37.
- Indian Ocean In Antiquity sur Google Livres.
- The Silk Roads: Highways of Culture and Commerce sur Google Livres.
- Deville 1871, p. 59.
- Libes 1810, p. 81.
- Goury 1833, p. 36.
- Algarotti 1739, p. 126.
- Benson 2009, p. 134.
- Darrigol 2012, p. 79-80.
- Benson 2009, p. 132.
- Balland 2007, p. 480.
- Benson 2009, p. 174.
- Moatti 2007, p. 35-37.
- Balland 2007, p. 150.
- Kovarski 2009, p. 569.
- Kovarski 2009, p. 682.
- Le guide des reflex numériques 2008: choisir, régler et utiliser les reflex sur Google Livres.
- Balland 2007, p. 82.
- Serway 1992, p. 168.
- Serway 1992, p. 162-163.
- Benson 2009, p. 118.
- Serway 1992, p. 292.
- Lanthony 1983, p. 136.
- Lanthony 1983, p. 79.
- Lanthony 1983, p. 81.
- Ghodssi et Lin 2011, p. 974.
- Balland 2007, p. 164.
- Balland 2007, p. 154-155.
- Balland 2007, p. 153.
- Balland 2007, p. 160-161.
- Balland 2007, p. 158.
- Williams 1976, p. 15-16.
- Williams 1976, p. 17-18.
- (en) Larry G. DeShazer, « Improved midinfrared polarizers using yttrium vanadate », SPIE proceedings, SPIE, polarization Analysis and Measurement IV, vol. 4481, no 10, (DOI 10.1117/12.452881, lire en ligne).
- (en) Dennis A. Vanderwerf, Applied prismatic and reflective optics, Bellingham, SPIE, , 296 p. (ISBN 978-0-8194-8332-4, DOI 10.1117/3.867634, lire en ligne), p. 61.
- (en) Johnson, W. Curtis, Jr., « Magnesium Fluoride Polarizing Prism for the Vacuum Ultraviolet », Review of Scientific Instruments, vol. 35, no 10, , p. 1375–1376 (ISSN 0034-6748, DOI 10.1063/1.1718763, lire en ligne, consulté le ).
- http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=4978162&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D4978162.
- (en) « Cookie Absent », sur aip.org (consulté le ).
Sites internet :
- (en) « Introduction to optical prisms », sur Edmund optics.
- (en) « Prisms » [PDF], sur Schott AG, .
- (en) « Prisms », Encyclopedia of Laser Physics and Technology, sur RP Photonics.
- (en) « Anamorphic prism pairs », Encyclopedia of Laser Physics and Technology, sur RP Photonics.
- (en) « Prism pairs », Encyclopedia of Laser Physics and Technology, sur RP Photonics.
- (en) « Polarizers », Encyclopedia of Laser Physics and Technology, sur RP Photonics.
Voir aussi
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]Ouvrages ayant servi à la rédaction de l'article :
- Livres anciens :
- Guillaume Édmé Charles Goury, Recherches historico-monumentales : concernant les sciences, les arts de l'antiquité et leur émigration d'Orient en Occident, Paris, Firmin Didot Frères, , 600 p. (lire en ligne)
- Édmé-François Jomard, Description de l'Egypte : Ou recueil des observations et des recherches qui ont été faites en Egypte pendant l'expédition de l'armée française, t. 2, Paris, Imprimerie Royale, , 298 p. (lire en ligne)
- Achille Deville, Histoire de l'art de la verrerie dans l'antiquité, Paris, A. Morel et Cie, , 349 p. (lire en ligne)
- Antoine Libes, Histoire philosophique des progrès de la physique, t. 2, , viii-291 (OCLC 489639597, lire en ligne)
- Francesco Algarotti (trad. Du Perron de Casterra), Le newtonianisme pour les dames : Ou entretiens sur la lumière, sur les couleurs et sur l'attraction, t. 2, Paris, Montalant, , 2e éd., 316 p. (lire en ligne)
- Livres en langue française :
- Harris Benson (trad. de l'anglais), Physique 3 : Ondes, optique et physique moderne, Laval, De Boeck, , 4e éd., 226 p. (ISBN 978-2-8041-0763-5, lire en ligne)Ouvrage traduit de l'anglais.
- Bernard Balland, Optique géométrique : Imagerie et instruments, Lausanne, Presses polytechniques universitaires romandes, coll. « Sciences appliquées », , 860 p. (ISBN 978-2-88074-689-6, lire en ligne)
- Alexandre Moatti, Einstein, un siècle contre lui, Paris, Odile Jacob, , 305 p. (ISBN 978-2-7381-2007-6, lire en ligne)
- Caroline Kovarski (dir.), L'opticien-lunetier : Guide théorique et pratique, Paris, Lavoisier, coll. « Tec&Doc », , 1634 p. (ISBN 978-2-7430-1088-1, présentation en ligne, lire en ligne)
- Raymond A. Serway, Physique III : Optique et physique moderne, Laval, Editions mémoire vivante, , 762 p. (ISBN 2-8041-1606-9, lire en ligne)Ouvrage traduit de l'anglais.
- Philippe Lanthony, Dictionnaire du strabisme : Physiologie et clinique, Maloine, , 196 p. (ISBN 0-8288-1813-4 et 978-0828818131, lire en ligne)
- Harris Benson (trad. de l'anglais), Physique 3 : Ondes, optique et physique moderne, Laval, De Boeck, , 4e éd., 226 p. (ISBN 978-2-8041-0763-5, lire en ligne)
- Livres en langue étrangère :
- (en) Olivier Darrigol, A history of optics : From greek antiquity to the nineteenth century, New York (US), Oxford university press, , 327 p. (ISBN 978-0-19-964437-7, LCCN 2011945380, lire en ligne)
- (en) F. Twyman, Prism and Lens Making : A Textbook for Optical Glassworkers, Taylor & Francis, , 2e éd., 640 p. (ISBN 0-85274-150-2, lire en ligne)
- (en) Dudley H. Williams, Spectroscopy, (lire en ligne)
- (en) Reza Ghodssi et Pinyen Lin, MEMS Materials and Processes Handbook, Springer, , 1224 p. (lire en ligne)






![{\displaystyle \arcsin {\left[n\sin {\left(A-\arcsin {\left({\frac {1}{n}}\right)}\right)}\right]}\leq i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f10e3e6eb4f34371c679397fbc9483d76d073cc)















