Compensateur de Soleil-Babinet


Le compensateur de Soleil-Babinet est une lame de retard biréfringente couramment employée en optique pour tourner la polarisation de différentes longueurs d'onde ou comme compensateur de phase. Il consiste en deux prismes biréfringents, généralement en quartz, qui coulissent l'un sur l'autre pour ajuster la différence de chemin optique entre l'axe rapide et lent de la polarisation, ou bien qui ne coulissent pas, l'ensemble du compensateur étant alors chariotable dans une direction orthogonale à l'axe optique. Cet élément optique porte le nom des inventeurs Jacques Babinet et Jean-Baptiste Soleil.
Histoire de deux composants[modifier | modifier le code]
Il existe deux variantes du dispositif: la première est le compensateur de Babinet décrit ci-dessus et le compensateur de Soleil, très légèrement différent et qui est utilisé dans les mêmes domaines.
Compensateur de Babinet[modifier | modifier le code]
Explication physique[modifier | modifier le code]
Le compensateur de Babinet est le compensateur le plus largement utilisé[1]. Il permet d'imposer un retard de phase contrôlé à un faisceau lumineux qui le traverse. Les deux prismes biréfringents et triangulaires ont des axes optiques croisés, c'est-à-dire orthogonaux .
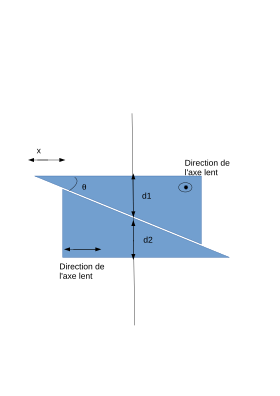
En notant et respectivement l'épaisseur locale du premier prisme et du deuxième prisme le long de l'axe optique du système à étudier et les indices ordinaires et extraordinaires du matériau, la différence de marche entre deux vibrations orthogonales entre elles et parallèles respectivement aux axes optiques des deux prismes du compensateur correspond à : [2].
Mesure de la biréfringence[modifier | modifier le code]
Le compensateur de Babinet permet de mesurer efficacement la biréfringence d'un matériau pour une lumière d'une certaine longueur d'onde. Il faut placer une lame de l'échantillon dont on souhaite mesurer la biréfringence sur un axe avec le compensateur de Babinet tous deux compris entre un polariseur et un analyseur, et à la suite de l'analyseur un oculaire permettra d'observer des franges d'interférences. Le polariseur et l'analyseur sont croisés.

Le principe de cette mesure est qu'en plaçant l'échantillon dont les lignes neutres sont parallèles à celles du Babinet alors les franges se déplacent proportionnellement à la différence de marche supplémentaire introduite par l'échantillon.
En effet la différence de marche totale est : avec δb la différence de marche introduite par le Babinet et δe la différence de marche introduite par l'échantillon. Or avec e l'épaisseur de la lame. Donc mesurer le déplacement de la frange centrale permet d'obtenir la différence de marche introduite par l'échantillon et donc la biréfringence.
Il faut tout d'abord étalonner le compensateur, c'est-à-dire mesurer la différence de marche introduite par le compensateur seul à une certaine longueur d'onde λ (la biréfringence pouvant dépendre de la longueur d'onde). Pour cela, on observe les franges avec une lumière considérée monochromatique de la longueur d'onde en question et on mesure l'interfrange: le déplacement i du compensateur entre deux franges sombres ou deux franges lumineuses. On a: .
Afin d'avoir un contraste maximum et d'observer les franges en lumière blanche: la direction du compensateur de Babinet doit être à 45° des directions du polariseur et de l'analyseur. Sans l'échantillon à mesurer sur l'axe optique, en éclairant le Babinet, on peut alors observer des franges correspondant aux teintes de Newton à frange centrale noire à travers le viseur. Il faut alors centrer la frange noire.
Ensuite on place la lame sur l'axe optique de manière que la frange noire reste centrée donc de manière que ses axes neutres soient parallèles aux directions du polariseur et de l'analyseur, puis on tourne la lame à 45° de manière que ses axes neutres soient parallèles aux directions du Babinet et on déplace le compensateur pour que la frange noire soit centrée. On mesure alors le déplacement x du Babinet.
La différence de marche du Babinet est alors θ étant l'angle des prismes.
On obtient alors la biréfringence du matériau de la lame Δn sachant la différence de marche sur la frange noire est égale à 0 : soit [3].
Direction de polarisation d'une lumière polarisée rectilignement[modifier | modifier le code]
Une autre application courante du compensateur de Babinet est l'analyse d'une lumière polarisée. Une lumière polarisée rectilignement oscille selon une seule direction de l'espace, il est alors possible de déterminer la direction de polarisation d'une telle lumière à l'aide du compensateur de Babinet et d'un analyseur.
Pour déterminer la direction de polarisation d'une lumière polarisée rectilignement avec ce système optique, il nous faut faire varier la position de l'analyseur : la différence de marche introduite par le compensateur de Babinet est . À partir de la position , , il suffit donc de tourner l'analyseur jusqu'à ce la frange centrale soit aussi sombre que possible, la direction de l'analyseur est alors parallèle au plan optique qui est lui-même orthogonal à la direction de polarisation. En repérant deux positions différentes de l'analyseur pour lesquelles l'intensité sur la frange centrale est minimale, on peut donc déterminer la direction de polarisation d'une onde polarisée rectilignement[4].
Analyse d'une lumière polarisée elliptiquement[modifier | modifier le code]
Une lumière polarisée elliptiquement oscille selon une ellipse et est caractérisée par les axes de l'ellipse que décrit son champ électrique avec b et a les demi-axes de l'ellipse avec par convention, et par son sens de propagation le long de l'ellipse[5]. On étudie en général une onde polarisée elliptiquement en la décomposant en deux autres vibrations: les éléments caractérisant la polarisation elliptique peuvent alors être retrouvés en obtenant le retard de phase entre ces deux ondes et le rapport de leur amplitude. Utiliser le compensateur est une méthode pour accéder à ces paramètres.
D'après le principe de superposition, on peut alors représenter une onde polarisée elliptiquement comme une somme de deux ondes polarisées rectilignement, chacune dans la direction d'un des axes de l'ellipse. Les composantes du champ électrique de l'onde selon ces axes que nous noterons x et y sont alors :
avec ω pulsation de l'onde et φ un angle représentant le retard de l'onde selon y par rapport à l'onde selon x[6]. Les deux ondes présentent alors une certaine différence de marche δ telle que pour une certaine longueur d'onde λ.
À l'aide du compensateur de Babinet, on peut déterminer cette différence de marche ainsi que les directions des axes de l'ellipse. Pour cela, on place sur l'axe optique seulement le compensateur et un analyseur.
Compensateur de Soleil[modifier | modifier le code]
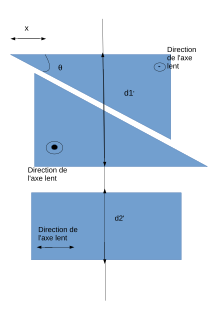
Une variante du compensateur de Babinet, qui se base sur le même principe est le compensateur de Soleil. Ce compensateur de Soleil est également constitué de deux prismes triangulaires dans un matériau biréfringent pouvant se déplacer l'un par rapport à l'autre, mais on ajoute une lame dont l'axe optique est orthogonal aux axes optiques des deux prismes qui sont maintenant parallèles.
Explication physique[modifier | modifier le code]
Ce dispositif se base sur le même principe que le compensateur de Babinet et a les mêmes applications pratiques, la méthode utilisée variant légèrement selon le compensateur qui introduit le retard sur la lumière traversant le système, mais a l'avantage sur celui-ci de produire un déphasage uniforme à travers le système.
En effet la différence de marche induite est alors . d1' est l'épaisseur totale, variable en fonction de la position des deux prismes et d2' l'épaisseur de la lame. Le déphasage est donc uniforme quel que soit le rayon traversant le dispositif[7]. En effet un inconvénient du compensateur de Babinet est que les faisceaux lumineux étudiés doivent être très étroits sans quoi il y aurait une différence importante entre la différence de marche introduite par le compensateur d'un point à un autre de l'image observée. Le compensateur de Soleil permet d'éviter qu'un faisceau lumineux grand n'introduise de trop grande erreur de mesure et apporte donc de la précision; de plus comme un faisceau lumineux plus élargi permet d'obtenir plus de luminosité sur l'image observée, il peut être plus avantageux d'utiliser ce compensateur.
Applications[modifier | modifier le code]
Le compensateur de Soleil est utilisé dans les mêmes domaines que le compensateur de Babinet: la méthode employée peut toutefois être différente selon le compensateur utilisé et peut aussi presque la même.
Mesure de la biréfringence[modifier | modifier le code]
Le mesure de la biréfringence est la même qu'avec le compensateur de Babinet dans le principe mais contrairement au compensateur de Babinet, elle ne permet pas de retrouver la biréfringence par cette seule mesure. Il faut adapter la mesure à la nouvelle expression de la différence de marche.
En effet la différence de marche introduite par le compensateur de Soleil est donc avec d1 épaisseur des deux prismes lorsqu'ils sont parfaitement emboités et x l'éloignement d'un des prismes par rapport à cette position. Pour simplifier, on utilisera la relation
On commence de même par étalonner le compensateur de Soleil pour la longueur d'onde λ pour laquelle on souhaite mesurer la biréfringence. Le compensateur est placé sur un axe optique avec un polariseur et un analyseur croisés, et avec un système permettant d'observer les figures d'interférence (écran ou microscope ou détecteur de luminosité), sans la présence de la lame dont on souhaite calculer la biréfringence et on éclaire ce système à l'aide d'une source lumineuse de longueur d'onde λ et de finesse convenable. On peut observer plusieurs franges noires et sachant que pour une frange noire la différence de marche est avec k entier relatif, en mesurant l'interfrange i entre deux franges consécutives, on en déduit et on détermine a de même que précédemment.On peut observer la frange sombre centrale pour laquelle δ=0 en éclairant en lumière blanche, et donc on peut en mesurer la position x0 pour laquelle δ=0.
Alors on place le compensateur à la position x0 et on place la lame dont on souhaite mesurer la biréfringence entre le polariseur et le compensateur de Soleil. La différence de marche totale introduite par le système est alors . Donc en se positionnant de même sur une frange sombre, on obtient une position x telle que avec k entier. On observe deux franges sombres en des positions x et x' telles que . En utilisant alors une valeur grossière de la biréfringence obtenue par exemple à l'aide de l'échelle des teintes de Newton, on peut déterminer k et ainsi la biréfringence Δn avec une grande précision[8].
Dans le cas de la mesure de la biréfringence, le compensateur de Soleil est ainsi plus délicat à utiliser que le compensateur de Babinet puisqu'il requiert d'avoir utilisé au préalable une mesure grossière de la biréfringence.
Analyse de la lumière polarisée elliptiquement[modifier | modifier le code]
Sources[modifier | modifier le code]
- Richard Taillet, Pascal Febvre et Loïc Villain, Dictionnaire de physique, De Boeck, coll. « De Boeck Supérieur », , 754 p., p. 102
- Germain Chartier, Manuel d'Optique, 301-302 p.
Notes et références[modifier | modifier le code]
- Physique des diélectriques sur Google Livres
- [1],TP l'université de Grenoble : Biréfringence, Polarisation rotatoire
- [2]
- Leçons d'optique physique, Volume 2 par Marcel Emile Verdet sur Google Livres
- [3]
- [4]
- Physique des diélectriques sur Google Livres
- [5]


























