Fonction (mathématiques)

En mathématiques, une fonction permet de définir un résultat (le plus souvent numérique) pour chaque élément d’un ensemble appelé domaine. Ce résultat peut être obtenu par une suite de calculs arithmétiques ou par une liste de valeurs, notamment dans le cas de relevé de mesures physiques, ou encore par d’autres procédés comme les résolutions d’équations ou les passages à la limite. Le calcul effectif du résultat ou son approximation repose éventuellement sur l’élaboration d'une fonction informatique.
Dans l’enseignement scolaire, le terme « fonction » concerne spécifiquement les fonctions réelles d’une variable réelle. De nombreuses fonctions dites usuelles sont ainsi définies comme les fonctions affines, la racine carrée ou l’exponentielle, et peuvent être combinées à l’aide des opérations arithmétiques, de la composition ou de la définition par morceaux.
Ces fonctions satisfont diverses propriétés portant sur la régularité, les variations, l’intégrabilité...
En théorie des ensembles, une fonction ou application est une relation entre deux ensembles pour laquelle chaque élément du premier est en relation avec un unique élément du second[1]. Parfois, on distingue la notion de fonction en affaiblissant la condition comme suit : chaque élément du premier ensemble est en relation avec au plus un élément du second.
En théorie des types, une fonction est la description de la méthode pour obtenir le résultat à partir de ses paramètres. Autrement dit une fonction est l'algorithme qui permet de la calculer.
Le terme de fonction s’emploie parfois pour désigner d’autres objets mathématiques apparentés comme des fonctions multivaluées (notamment holomorphes), les classes de fonctions p-intégrables ou les distributions telle la fonction de Dirac.
Vocabulaire et notations
[modifier | modifier le code]Par défaut, une fonction est souvent notée ou , et si d'autres notations de fonctions sont nécessaires au sein d'un même raisonnement, on utilise en général les lettres suivantes dans l'alphabet latin, voire dans l'alphabet grec en commençant par φ ou ψ.
définie par l’expression
Une fonction est souvent définie par son expression, dépendant en général d’une ou plusieurs variables, le plus souvent ou . En remplaçant les variables par des valeurs explicites dans l’expression, on obtient une valeur de la fonction.
Dans le cadre de l’analyse réelle, les fonctions ont des variables réelles, mais certaines valeurs réelles ne peuvent être employées dans l’expression et sont appelées valeurs interdites. C’est le cas par exemple de zéro pour la fonction inverse, car on ne peut pas diviser par zéro. Par défaut, on considère souvent que la fonction est définie partout en dehors des valeurs interdites. Cependant, on peut aussi spécifier un domaine de définition qui rassemble toutes les valeurs possibles pour les variables (assimilé à l’ensemble de départ ou source pour une application) et un ensemble d'arrivée (but) qui contient toutes les valeurs possibles de la fonction.
Ces informations peuvent être résumées par un diagramme comme suit, où la flèche entre les ensembles source et but est une simple flèche vers la droite (→), tandis que celle entre la variable et l’expression est munie d’un taquet (↦) :
ou, pour une fonction définie sur un ensemble à valeurs dans un ensemble :
Une fonction peut être définie par plusieurs expressions valables sur des domaines disjoints, comme la fonction valeur absolue :
Le domaine de définition d’une fonction est classiquement noté . L'ensemble image, c'est-à-dire l'ensemble des valeurs possibles pour le résultat, est alors noté ou , et par définition inclus dans l’ensemble but. Étant donné une valeur dans le domaine de définition, et un élément de l’ensemble but tel que , on dit que est l’(unique) image de et que est un antécédent de . Par exemple, 9 est l'image de 3 par la fonction carré, et 3 est donc un antécédent de 9 (mais ce n'est pas le seul, puisque −3 est aussi un antécédent de 9).
Étude
[modifier | modifier le code]Typologie
[modifier | modifier le code]Les méthodes d'analyse des fonctions diffèrent selon la nature de la variable et du résultat. On distingue notamment :
- les fonctions réelles d’une variable réelle
- les fonctions réelles de plusieurs variables réelles
- les fonctions holomorphes et méromorphes à variables et valeurs complexes
- les fonctions à variables et valeurs vectorielles, étudiées le plus souvent comme arcs et surfaces paramétrées ou comme champ vectoriels
- les fonctions différentiables définies sur des variétés différentielles à valeurs numériques ou dans d’autres variétés
- les fonctions arithmétiques à variable entière et à valeurs complexes
- les fonctions booléennes à variables et valeurs dans l’algèbre de Boole
- les fonctions aléatoires (ou processus stochastiques) dont les valeurs sont des variables aléatoires
- les fonctions cardinales dont les valeurs sont des nombres cardinaux
Représentation graphique
[modifier | modifier le code]
L’ensemble des couples définit le graphe de la fonction. Dans le cas d’une fonction réelle d'une variable réelle, ce graphe est inclus dans le plan et se présente comme une courbe appelée courbe représentative, sur laquelle on peut faire figurer les extrema locaux, certaines tangentes ou demi-tangentes, les asymptotes et mettre en évidence les variations et les zones de convexité ou concavité. Cette représentation permet aussi de visualiser les points d’annulation ou zéros de la fonction, son signe, et éventuellement une majoration ou minoration, sa parité et sa périodicité.
Une fonction définie par une liste de valeurs numériques peut être représentée par un nuage de points, une courbe polygonale ou un diagramme en barres.
Pour une fonction réelle de deux variables, le graphe correspond en général à une surface dans l’espace , sur laquelle on peut faire apparaitre des lignes de niveau, en utilisant éventuellement un code couleur pour mettre en évidence le relief.
Pour une fonction vectorielle ou holomorphe, on peut représenter un champ de vecteur ou utiliser la coloration de régions.
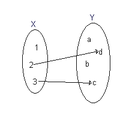
-
Diagramme sagittal d’une fonction partielle
-
Courbe polygonale représentant une fonction définie par une série chronologique
-
Surface représentative d’une fonction de 2 variables
-
Champ de vecteurs dans le plan
-
Coloration de régions pour la fonction complexe zêta de Riemann
Modes de définition
[modifier | modifier le code]
Une fonction peut être définie point par point par une expression explicite faisant intervenir d’autres fonctions de référence, des limites ou d’autres procédés algorithmiques. Il peut s’agir par exemple de la réciproque d’une autre fonction. Une même fonction peut d’ailleurs être définie par des formules différentes dont on montre l’égalité, comme dans le cas de la fonction exponentielle.
Une fonction peut aussi être définie globalement par une équation ou un système d'équations. En particulier, on définit une fonction implicite si l’ensemble des solutions d’une équation à deux inconnues x et y peut correspondre au graphe d’une fonction, c’est-à-dire si pour toute valeur de x il existe au plus une solution de la forme . Une fonction peut aussi être définie de proche en proche par une équation différentielle voire une équation aux dérivées partielles, ou par récurrence dans le cas d’une fonction arithmétique.
On peut encore définir une fonction sur un ensemble dense dans un autre et étendre la définition par continuité. Ce procédé permet notamment de justifier l’existence de la courbe de Peano et d’autres fonctions continues mais nulle part dérivable. Il peut être utilisé aussi pour définir des fonctions sur un corps de nombres p-adiques.
Tous ces procédés de détermination mathématique s’accompagnent de problèmes de calcul effectif, qui s’étudient dans le cadre de l’analyse numérique.
Analyse
[modifier | modifier le code]
L’analyse mathématique s’entend le plus souvent dans l’étude d’une fonction numérique, avec la recherche de son signe et de ses variations, la détermination d’éventuels majorant ou minorant, points fixes et limites, voire le calcul de son intégrale.
Plus généralement, on peut essayer de déterminer si une fonction est injective, c’est-à-dire si tout élément de l’ensemble d’arrivée a au plus un antécédent. Dans ce cas, on s’intéresse à la détermination de l’ensemble image, car la fonction admet alors une réciproque de son ensemble image vers son ensemble de définition. La précision de l’ensemble de définition est ici cruciale, comme dans le cas de la fonction carré (qui est n’est pas injective si elle est définie sur , mais qui l’est par restriction à l’ensemble ) ou de la fonction exponentielle (injective en tant que fonction d’une variable réelle, mais pas en tant que fonction d’une variable complexe).
Pour une fonction arithmétique, donc définie sur l’ensemble des entiers naturels, on s’intéresse notamment aux relations entre l’image d’un produit et les images des facteurs (surtout lorsque ceux-ci sont premiers entre eux).
Image directe et image réciproque
[modifier | modifier le code]Étant donné un sous-ensemble A de l’ensemble de départ, l’image directe est l’ensemble des images des éléments de A par f. Réciproquement, étant donné un sous-ensemble B de l’ensemble d’arrivée, sa préimage ou image réciproque est l’ensemble des antécédents des éléments de B par f.
Ces notions permettent notamment d’exprimer la continuité d’une fonction entre espaces topologiques, de caractériser l’existence de limites, de justifier qu’une fonction est mesurable afin de pouvoir envisager son intégrabilité.
Historique de la notion
[modifier | modifier le code]
La définition du concept de fonction a évolué depuis son introduction par Leibniz à la fin du XVIIe siècle[2]. Il s'agissait alors d'associer un objet à chaque point d'une courbe, par exemple la tangente. En identifiant chaque point de la courbe avec son ordonnée, Jean Bernoulli puis Euler redéfinissent ensuite ce terme pour décrire une expression composée d'une variable et d'éventuels paramètres constants (réels). Les opérations utilisées comprennent non seulement les opérations algébriques élémentaires, les séries et produits infinis mais aussi l'exponentielle, le logarithme et les lignes trigonométriques, considérés comme des opérations transcendantes.
Le lien entre l'expression d'une fonction et sa courbe représentative conduit Euler à élargir la notion en admettant des définitions par morceaux puis des courbes qui ne peuvent être obtenues par des expressions analytiques. La condition de continuité est formalisée par Bolzano et Cauchy au début du XIXe siècle. En 1829, l'étude des séries de Fourier conduit Dirichlet à considérer des fonctions plus générales, telle que l'indicatrice des rationnels[3],[4].
Parallèlement, le domaine de la variable s'ouvre aux nombres complexes. Au début du XXe siècle, les fonctions acceptent plusieurs variables, puis peuvent être définies sur un ensemble quelconque. Sous l'impulsion de Fréchet, la valeur d'une fonction suit la même généralisation. La théorie de l'intégration et l'analyse fonctionnelle vont plus loin en considérant des fonctions presque partout définies, nécessaires pour obtenir une structure d'espace de Banach sur les espaces Lp de fonctions -intégrables.
En analyse complexe, le prolongement analytique des fonctions holomorphes entraîne la prise en compte de fonctions multivaluées sur l'ensemble des complexes, réalisées formellement comme des fonctions classiques définies sur une surface de Riemann.
Notes et références
[modifier | modifier le code]- Définition que l'on trouve par exemple dans Paul Halmos, Introduction à la théorie des ensembles [détail des éditions], p. 40.
- Georges Papy, Mathématique moderne, vol. 1, Didier, , p. 315 : « Le mot de fonction a été introduit par Leibniz en 1694 ».
- Lejeune-Dirichlet, « Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données », J. reine angew. Math., vol. 4, , p. 157-169 (lire en ligne).
- Le nom de Dirichlet est associé à une définition plus moderne de fonction par Hermann Hankel. Voir (de) H. Hankel, Untersuchungen über die unendlich oft oscillirenden und unstetigen Functionen, (lire en ligne), p. 5. Sur cette évolution de la notion de fonction, on pourra lire : Imre Lakatos, Preuves et réfutations, Hermann, 1984, p. 194.
Voir aussi
[modifier | modifier le code]Articles connexes
[modifier | modifier le code]- Application (mathématiques)
- Analyse (mathématiques)
- Fonction numérique
- Fonction réelle d'une variable réelle
- Fonction de plusieurs variables
- Distribution (mathématiques)
- Fonction (mathématiques élémentaires)
- Qu'est-ce qu'une fonction ?, de Gottlob Frege
Bibliographie
[modifier | modifier le code]- Christian Houzel, « Fonction (notion de) », Dictionnaire des mathématiques – algèbre, analyse, géométrie, Encyclopædia Universalis et Albin Michel, Paris, 1997.
- Stella Baruk, « Fonction », Dictionnaire des mathématiques élémentaires, Éditions du Seuil, 1995.