Fonction puissance
En mathématiques, et plus spécialement en analyse, les fonctions puissances sont les fonctions fa définies par
où a peut désigner un entier naturel, un entier relatif, un réel voire un complexe que l'on appelle l'exposant de la fonction puissance. Selon la nature de a, l'ensemble de définition de la fonction fa peut changer.
Définie en général comme fonction de la variable réelle, on peut la trouver dans certains cas comme fonction complexe. Les fonctions puissances à exposant entier servent de base dans la construction des fonctions polynomiales et dans les développements en séries. Les fonctions puissances à exposant réel servent à modéliser des relations tant en physique qu'en biologie ou en économie.
Fonction de la variable réelle[modifier | modifier le code]
Exposant entier naturel[modifier | modifier le code]

Ce sont les fonctions définies sur ℝ par
Pour n pair, la fonction associée est paire, c'est-à-dire que, pour tout réel x, f(–x) = f(x), et la courbe représentative possède l'axe des ordonnées comme axe de symétrie.
Pour n impair, la fonction est impaire, c'est-à-dire que, pour tout réel x, f(–x) = –f(x), et la courbe représentative possède le point O comme centre de symétrie.
Les premières valeurs de n correspondent à des fonctions de référence :
- pour n = 1, il s'agit de la fonction identité f(x) = x ;
- pour n = 2, il s'agit de la fonction carré ;
- pour n = 3, il s'agit de la fonction cube ;
- le cas n = 0 est à étudier de près : par convention, on dira que la fonction x ↦ x0 est la fonction constante 1.
Toutes ces fonctions prennent la valeur 1 en 1. Plus l'exposant augmente, plus la courbe s'écrase sur l'axe des abscisses entre –1 et 1, et plus sa pente est raide en dehors de cet intervalle. En particulier, si m < n, alors pour tout x de l'intervalle ]0, 1[, xn < xm et pour tout x strictement supérieur à 1, xn > xm.
La fonction constante 1 étant mise à part, les fonctions puissances sont toutes strictement croissantes sur l'ensemble des réels positifs. Leur limite en plus l'infini est toujours plus l'infini et leur valeur en 0 est toujours 0. Pour un exposant strictement supérieur à 1, la courbe possède, en plus l'infini et en moins l'infini, une branche parabolique d'axe (Oy). Sur l'ensemble des réels négatifs, il faut distinguer le cas des exposants pairs non nuls pour lesquels la fonction est décroissante, et le cas des exposants impairs, pour lesquels la fonction est strictement croissante. Si l'exposant est impair et différent de 1, la courbe possède un point d'inflexion à l'origine.
Une fonction puissance est toujours dérivable sur ℝ. Si l'exposant est nul, la dérivée de f est nulle ; sinon, sa fonction dérivée est : . Ceci peut se démontrer par exemple en revenant à la définition du nombre dérivé et en utilisant le binôme de Newton.
Enfin, une telle fonction possède toujours des primitives définies par
Les fonctions puissances à exposant entier servent à construire les fonctions polynomiales. On les retrouve aussi dans le développement en série entière des autres fonctions.
Exposant entier négatif[modifier | modifier le code]
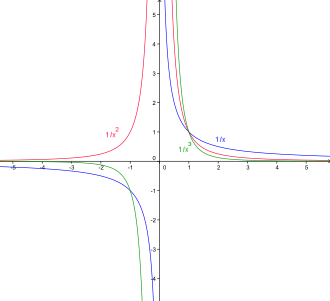
Ce sont les fonctions définies sur ℝ* par De même que fn, la fonction f–n est paire pour n pair et impaire pour n impair.
La première valeur de n correspond à une fonction de référence :
- pour n = 1, il s'agit de la fonction inverse. C'est la seule des fonctions puissances dont la représentation graphique donne une hyperbole.
Toutes ces fonctions prennent la valeur 1 en 1. Plus l'exposant augmente, plus la courbe s'écrase sur l'axe des abscisses avant –1 et après 1, et plus sa pente est raide dans les intervalles ]–1 ; 0[ et ]0 ; 1[. En particulier, si m < n alors, pour tout x de l'intervalle ]0 ; 1[, x–n > x–m et pour tout x supérieur à 1, x–n < x–m.
Ces fonctions puissances sont toutes strictement décroissantes sur l'ensemble des réels positifs. Leur limite en plus l'infini est toujours 0 et leur limite en 0 par valeurs positives est toujours plus l'infini. La courbe possède donc deux asymptotes, d'équations x = 0 et y = 0. Sur l'ensemble des réels négatifs, il faut distinguer le cas des exposants pairs non nuls pour lesquels la fonction est croissante, et le cas des exposants impairs, pour lesquels la fonction est strictement décroissante.
Une telle fonction puissance est toujours dérivable sur ℝ* :
En effet,
Une telle fonction possède toujours des primitives définies sur ]–∞ , 0[ ou sur ]0 , ∞[ par pour n différent de 1 ou par
Racines n-ièmes[modifier | modifier le code]

Pour tout entier naturel non nul n, la fonction fn est une bijection
- de [0, +∞[ sur [0, +∞[ si n est pair
- de ℝ sur ℝ si n est impair
La réciproque s'appelle la racine n-ième, et peut aussi s'écrire sous forme de puissance :
Sa limite en +∞ est toujours +∞ mais la courbe est tournée vers l'axe des abscisses. On parle alors de branche parabolique d'axe Ox. Dans un repère orthonormal, la courbe représentative de f1/n est symétrique de celle de fn (restreinte éventuellement à [0, +∞[) par rapport à la droite d'équation y = x.
Cette fonction est dérivable sur son ensemble de définition sauf en 0 où la courbe possède pour tangente l'axe des ordonnées. La dérivée de f1/n se calcule à l'aide de la dérivée de la fonction réciproque et s'exprime par :
Elle possède sur son ensemble de définition des primitives définies par
Exposant réel[modifier | modifier le code]
Étude générale[modifier | modifier le code]
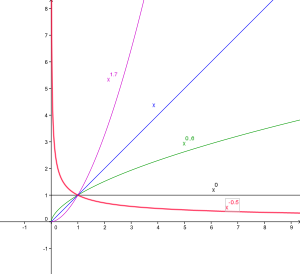
Grâce aux fonctions exponentielle et logarithme, on peut généraliser les fonctions puissances à tout exposant a réel. Pour tout réel x strictement positif, la fonction fa est alors définie par:
Selon les valeurs de a, elle est parfois prolongeable par continuité en 0 (voire à ℝ* ou ℝ (cf supra)). Selon les valeurs de a, le prolongement peut ou non être dérivable en 0. le sens de variation dépend du signe de a.
La convexité d'une fonction est liée au signe de sa dérivée seconde. Ici la convexité d'une fonction puissance est liée au signe de a(a–1).
| Valeur de a | Prolongeable en 0 | Dérivable en 0 | Sens de variation | Comportement à l'infini | Convexité |
|---|---|---|---|---|---|
| a < 0 | non | non | décroissante | asymptote d:y = 0 | convexe |
| a = 0 | oui | oui | constante | confondue avec d:y=1 | droite |
| 0 < a < 1 | oui | non | croissante | branche parabolique d'axe Ox | concave |
| a = 1 | oui | oui | croissante | confondue avec d:y=x | droite |
| a > 1 | oui | oui | croissante | branche parabolique d'axe Oy | convexe |
Dérivée et primitive[modifier | modifier le code]
La fonction puissance est toujours dérivable sur ]0 ; +∞[ et sa dérivée s'exprime toujours sous la forme
Pour un exposant a différent de -1, elle possède toujours des primitives sur ce même intervalle définies par
Pour l'exposant –1, on retrouve comme primitive la fonction logarithme népérien appelé aussi parfois logarithme hyperbolique en référence à l'aire sous l'hyperbole représentant la fonction inverse.
Croissances comparées[modifier | modifier le code]
Les fonctions logarithmes et exponentielle de base b > 1 et les fonctions puissances d'exposant a > 0 ont toutes une limite infinie en +∞. Il est donc intéressant de définir leur force respective et de comparer leur croissance.
On démontre qu'en +∞, l'exponentielle est toujours plus forte que la puissance et cette dernière est toujours plus forte que le logarithme.
Cela signifie que pour tout b > 1 et tout a > 0,
Infiniment petit et fonction höldérienne[modifier | modifier le code]
Pour a strictement positif, on a . On peut dès lors chercher à comparer la force de cette convergence avec la force de convergence d'autres fonctions.
Ainsi on dira que f est un infiniment petit d'ordre supérieur ou égal à n au voisinage de 0 si est borné sur un intervalle ouvert contenant 0[1],[2].
On dit que f est a-höldérienne sur un intervalle I s'il existe un réel M tel que, pour tous réels x et y de I,
En général, on prend a compris entre 0 et 1 car si a est strictement supérieur à 1, cette condition conduit à dire que f est constante sur I.
La fonction puissance d'exposant a, pour 0 < a ≤ 1, est l'exemple le plus simple de fonction a-höldérienne. En effet, pour tous réels x ≥ y ≥ 0,
- [3].
Fonction à rapport constant[modifier | modifier le code]
Théorème — Une fonction f : ]0, +∞[ → ℝ, non identiquement nulle et continue en au moins un point, vérifie l'équation fonctionnelle f(xy) = f(x)f(y) si et seulement si elle est de la forme x ↦ xa pour un certain réel a.
Par conséquent, une fonction f : ]0, +∞[ → ℝ* continue en au moins un point est proportionnelle à une fonction puissance si et seulement si elle vérifie la propriété suivante : des rapports de x égaux induisent des rapports de f(x) égaux, c'est-à-dire :
Développement en série[modifier | modifier le code]
La fonction fa est développable en série entière au voisinage de x0 selon la formule
où
sont des coefficients binomiaux généralisés.
On remarque que pour a entier naturel, la somme comporte un nombre fini de termes : il s'agit de la formule du binôme. Le rayon de convergence de cette série est alors infini.
Si a n'est pas entier naturel, la somme comporte une infinité de termes et le rayon de convergence est de . Voir aussi Fonction hypergéométrique#Cas particuliers.
Utilisations[modifier | modifier le code]
La multiplicité des formes de courbes de fonctions puissances en fait de bons candidats pour des modélisations de phénomènes en physique, biologie[4], allométrie ou économie. Dès que l'on observe que la courbe exprimant y en fonction de x a une allure ressemblant aux courbes précédemment décrites, on peut proposer un modèle de la forme
Par abus de langage, on parle alors encore de fonctions puissances et l'on écrit que y est une fonction puissance de x.
On cherche aussi une modélisation de ce type dès que des rapports égaux entre valeurs de x induisent des rapports égaux entre les valeurs de y.
Dans cette modélisation, il s'agit de trouver la meilleure valeur de K et de a modélisant cette relation. On peut chercher a sous forme rationnelle, on cherche alors deux entiers p et q tels que
- ,
ou encore deux entiers relatifs p' et q tels
- .
Pour des courbes de type a < 1, on cherche p' et q positifs ; pour des courbes de type 0 < a < 1, on cherche des entiers p' et q de signes contraires, l'exposant de y étant, en valeur absolue, supérieur à l'exposant de x. Enfin, pour a > 1, on cherche des exposants de signes contraires, celui de x étant en valeur absolue plus grand que celui de y.

Ainsi par exemple pour mettre en place la troisième loi de Kepler, donnant la relation entre le demi-grand axe de la trajectoire d'une planète et la période de celle-ci, on peut observer que la courbe donnant la période en fonction du demi-grand axe est du type puissance avec a > 1. À partir du tableau de mesures,
| Planète | demi grand axe R en 109 m | période T en 106 s |
| Mercure | 57,9 | 7,58 |
| Vénus | 108,2 | 19,36 |
| Terre | 149,6 | 31,47 |
| Mars | 227,9 | 59,19 |
| Jupiter | 778,3 | 373,32 |
on cherche donc à vérifier si T/R2 ou T2/R3 est constante. La seconde tentative est la bonne et donne une constante d'environ 2,96 × 10–4.
Lorsque la relation est plus compliquée, il est préférable de procéder à un ajustement logarithmique. En effet, si la relation entre y et x est telle que
alors il doit exister une relation affine entre ln(x) et ln(y) :
Un ajustement linéaire sur le nuage de points (ln(x), ln(y)) permet alors de retrouver la fonction puissance liant x et y. Si
alors
Pour vérifier si un ajustement sous forme de fonction puissance est envisageable, il suffit donc de placer le nuage de points dans un repère log-log. Si les points semblent alignés, un ajustement par une fonction puissance est envisageable.
Dans le domaine économique, les courbes de concentration de Lorenz donnent sur l'intervalle [0;1] des courbes que l'on peut modéliser par des fonctions puissances. Cette modélisation est légitime lorsque les phénomènes étudiés suivent tous deux une loi de Pareto[5].
Fonction de la variable complexe[modifier | modifier le code]
Pour la variable complexe, on peut définir sur , la fonction , pour tout entier naturel n. Ces fonctions servent à construire les fonctions polynomiales sur et à construire le développement en série des fonctions holomorphes. Il est aussi possible de définir sur , la fonction , pour tout entier négatif.
Mais il n'est pas possible de définir sur de manière univoque za, où a est un complexe ou réel. En effet, il faut se limiter à un ouvert de dans lequel il existe une détermination L du logarithme complexe. Dans un tel ouvert, fa est alors une fonction holomorphe définie par[6]:
Notes et références[modifier | modifier le code]
- Jacqueline Lelong-Ferrand et Jean-Marie Arnaudiès, Cours de mathématiques, T2, Bordas, Paris, 1977, p. 147.
- On trouve aussi, chez Paul Appell[réf. incomplète] : f est un infiniment petit d'ordre a si au voisinage de 0, ou bien encore, de manière plus restrictive, f est un infiniment petit d'ordre a si possède une limite en zéro ni nulle, ni infinie (Evgeny Chikine, Mathématiques supérieures, pour ingénieurs et polytechniciens).
- Voir par exemple .
- André Ross, Fonction puissance et modélisation, Cégep de Lévis-Lauzon.
- Marc Barbut, « Note sur quelques indicateurs globaux de l'inégalité : C. Gini, V. Pareto, P. Lévy », Revue de sociologie française, vol. 25, no 25-4, 1984, p. 609-622.
- Noëlle POTTIER, Matière et Systèmes Complexes,«Chap. 4 Fonctions analytiques», Université Paris 7- Denis Diderot










![{\displaystyle f_{n}^{-1}(x)={\sqrt[{n}]{x}}=x^{1/n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b19315df753542ae2ab8b2e075b78829c86036d4)




























