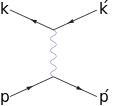
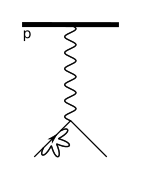
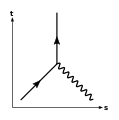
Diagramme de Feynman

Le temps est ici en abscisse, de gauche à droite ; l'espace est en ordonnée.
Les flèches symbolisent le type de l'objet (particules ">", vers le futur, et anti particule "<") et non un sens de déplacement ; photons, gluons etc. ont leur propres symboles (Cf. infra).
En physique théorique, les diagrammes de Feynman sont un système de représentation graphique des équations décrivant les interactions des particules subatomiques dans le cadre de la théorie quantique des champs. Le physicien américain Richard Feynman a inventé ces diagrammes à la fin des années 1940, à l’université Cornell, face à la difficulté de ses calculs de diffusion des particules. Ce système a révolutionné toute la physique théorique, avant d'être utilisé en physique appliquée.
Les calculs d'amplitudes de probabilité font intervenir des intégrales complexes mais présentant une structure régulière qui les rend représentables par des diagrammes et des conventions.
Un diagramme typique représente deux particules qui se joignent, d'un côté, face à deux autres qui se séparent, le lien entre ces paires successives étant lui-même représenté plus ou moins conventionnellement. Malgré leur aspect, les diagrammes de Feynman ne figurent pas des événements physiques. Les seuls éléments réels sont les particules entrantes et sortantes du graphe, et non les interactions décrites par le diagramme.
Histoire[modifier | modifier le code]

Les diagrammes de Feynman ont révolutionné la physique des particules en rendant accessibles, au travers de figures simples, des calculs et des concepts abstraits[2]. Leur concept a ensuite été utilisé en physique nucléaire, pour la théorie de la gravitation ou encore la physique du solide : ils se sont diffusés à l'ensemble de la physique[3]. Julian Schwinger les a comparés au développement de l'ordinateur : « tout comme la puce électronique des dernières années, le diagramme de Feynman a démocratisé le calcul »[Note 1],[4]. Leur importance est telle que les historiens des sciences leur ont associé une catégorie spécifique : Andrew Warwick a créé le terme de « technologie théorique », et Ursula Klein (en) celui des « outils de papier »[5].
Feynman les a inventés pour effectuer des calculs de dispersion en électrodynamique quantique. Pour simplifier ses calculs sur les amplitudes de probabilité, il a associé les termes mathématiques à des graphes représentant les particules par des lignes et leurs interactions par un vertex, intersection entre les lignes[6]. Plus prosaïquement, sa première idée a été la création d'un système de notation lui permettant de suivre les calculs gigantesques nécessaires en électrodynamique quantique[7]. Lorsqu'il les a présentés au printemps 1948, quasiment aucun physicien ne semblait en comprendre le sens[Note 2]. Mais dans les mois qui suivent, chacun les a adoptés avec ses propres conventions. Malgré un début de standardisation dès 1949, de nombreuses familles de diagrammes se sont développées pour diverses utilisations, remplaçant même des outils existants[8].
Durant les six premières années, les diagrammes se sont diffusés à une centaine de physiciens par le bouche à oreille et les articles scientifiques ; les premiers livres en anglais sur le sujet sont parus en 1955[Note 3],[9]. Cette diffusion ne s'est pas faite seule, mais principalement grâce au travail de Freeman Dyson, arrivé à Cornell en 1947 pour travailler avec Hans Bethe. Associé de Feynman, il a beaucoup discuté avec lui de cette méthode graphique facilitant les calculs de renormalisation. Il a aussi étudié la méthode purement algébrique de Julian Schwinger ainsi que les méthodes de Sin-Itiro Tomonaga et finalement démontré que les trois approches étaient équivalentes, fournissant en plus un mode d'emploi sur l'application des diagrammes de Feynman alors que ce dernier n'avait pas encore publié d'article sur le sujet[10].
Avant Feynman, les quelques représentations graphiques créées pour essayer de rendre plus intuitifs les concepts de la mécanique quantique étaient loin d'être aussi complètes. Il y a eu en particulier le diagramme des transitions entre niveaux d'énergie (inspiré des schémas de la spectroscopie) et le diagramme imaginé par Gregor Wentzel pour décrire les processus d'échange entre particules[Note 4],[11]. Feynman s'est aussi inspiré des diagrammes de Minkowski, utilisés en relativité restreinte[12].
Description[modifier | modifier le code]
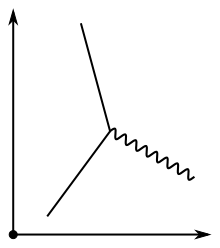
Les diagrammes de Feynman sont des représentations graphiques de termes utilisés dans des calculs perturbatifs. N'ayant jamais été standardisés, de nombreuses conventions existent, d'autant plus qu'ils ont des applications très variées au-delà des interactions entre particules[13]. Par leur nature en physique quantique, ils sont une façon élégante de passer de la description d'un processus d'interaction entre des électrons et des photons à la formule mathématique qui donne son amplitude de probabilité[14]. Avec le temps, les diagrammes sont devenus un langage permettant aux physiciens de parler de leurs calculs[15].
Sous leur apparence simple, ces diagrammes qui semblent décrire de manière figurative les interactions entre particules, sont en fait des outils mathématiques puissants. Richard Feynman les a créés pour réaliser des calculs en électrodynamique quantique[3]. Ils ont ensuite été généralisés à toutes les interactions dont les particules sont connues, c'est-à-dire les interactions électromagnétique, forte et faible. Les fermions sont représentés par une ligne fléchée, les antifermions par une ligne avec une flèche en sens inverse, les bosons de jauge ont des représentations distinctes : le photon par une ligne ondulée, le gluon par une ligne en boucles, les bosons W, Z et de Higgs par une ligne en pointillé accompagnée de leur symbole (W+, W−, Z, H) ; les bosons de l'interaction faible (W+, W−,Z) sont parfois représentés avec la même ligne ondulée que le photon[16].
- Particules élémentaires
-
fermion -
antifermion -
photon -
gluon -
boson massif
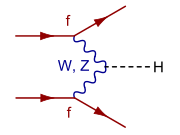
Exemples de diagrammes utilisant plusieurs types de particules :
| Réactions de création du boson de Higgs les plus probables[17] | |||||||||
| |||||||||
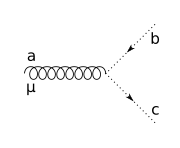
Le fantôme de Faddeev-Popov (en) est tracé avec une ligne de points[18] :
| Vertex antifantôme-fantôme-gluon | |||||||||
| |||||||||
Représentation des autres particules[modifier | modifier le code]
Les diagrammes de Feynman n'ayant été standardisés, même pour les interactions élémentaires, certaines peuvent avoir des représentations très différentes souvent adaptées au contexte. Le proton, qui est une particule composite, peut apparaître sous la forme d'une ligne fléchée accompagnée de la lettre , d'un cercle qui représente plus généralement les hadrons ou de trois lignes parallèles représentant les deux quarks u et le quark d :
Conventions[modifier | modifier le code]
Un phénomène lumineux ou électronique, représenté dans un diagramme de Feynman, est appelé « séquence »[19]. Les séquences se déroulent dans l'espace-temps, représenté dans un repère avec l'espace en abscisse, simplifié à une seule dimension au lieu de trois, et le temps en ordonnée[20]. Feynman préférait orienter le temps vers le haut, ce choix étant purement arbitraire, mais les physiciens des particules semblent préférer de plus en plus l'orientation de gauche à droite[Note 5],[21].
- Conventions d'espace et de temps
-
Temps vers le haut, convention de Feynman -
Temps vers la droite, convention constatée
Les fermions sont représentés par une ligne droite orientée par une flèche et les particules vectrices de force (les bosons) par une ligne ondulée ou en pointillé. La séquence d'émission ou d'absorption d'un photon est appelée « jonction » ou « couplage » ; elle est représentée par un vertex, point de jonction des lignes[22]. Le couplage nomme indifféremment l'émission ou l'absorption parce que les deux phénomènes ont la même amplitude, égale à la constante de structure fine pour l'électrodynamique quantique ou à la constante de couplage de l'interaction nucléaire forte pour la chromodynamique quantique.
Un diagramme est construit avec trois éléments : des vertex où l'énergie et l'impulsion sont conservées, des lignes externes représentant les particules réelles qui entrent et sortent, et des lignes internes représentant des particules virtuelles[15]. À chaque ligne ou vertex est associé un facteur qui contribue à l'amplitude de probabilité du processus décrit, le facteur associé à une particule virtuelle (ligne interne) est nommé propagateur[23].
Propriétés[modifier | modifier le code]

Une interaction est décrite par un ensemble de diagrammes de Feynman et définie par ses particules entrantes et sortantes. Il est possible de mesurer les propriétés de ces particules, comme leur énergie ou leur quantité de mouvement et de vérifier qu'elles respectent l'équation d'équivalence masse-énergie d'Einstein, , dans sa version relativiste (conservation du quadri-moment)[24]. On dit que les particules ainsi observables sont sur leur couche de masse[25].
En revanche, tout ce qui se trouve au milieu, qui n'entre ni ne sort, n'est pas mesurable : ce sont des particules virtuelles, elles ne vérifient pas l'équivalence masse-énergie, ne sont pas limitées par la vitesse de la lumière et ne sont pas non plus tenues de suivre la flèche du temps. On dit qu'elles sont hors couche[26].
Pour analyser un processus physique dont on connaît les particules entrantes et sortantes, les diagrammes de Feynman permettent de représenter l'infinité des réactions possibles qui interviennent entre ces lignes externes. Chaque diagramme produit, grâce aux règles de Feynman, un nombre complexe[Note 6] et la somme de tous ces nombres est égale, à un facteur près, à l'amplitude de diffusion du phénomène. L'efficacité de cette méthode provient du fait que chaque vertex est associé à un facteur proportionnel à une constante de couplage, qui a une valeur très petite. Par exemple, en électrodynamique quantique, elle vaut : .
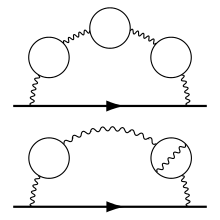
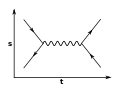
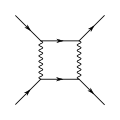
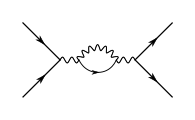
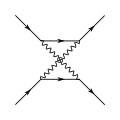
Comme les facteurs d'un diagramme sont multipliés pour donner son amplitude, tous les diagrammes qui ont un grand nombre de vertex ont une contribution négligeable ; il est donc rare d'utiliser les diagrammes qui possèdent plus de quatre vertex puisque l'on obtient déjà une approximation valable avec six chiffres significatifs[27].
- Exemples de diagrammes à quatre vertex
Pour des cas particuliers, il est nécessaire de pousser la précision du calcul aux ordres supérieurs. Par exemple en 2012, pour calculer la valeur de la constante de structure fine, une équipe de physiciens a mesuré le facteur de Landé dans un cyclotron pour le comparer à un calcul théorique à l'ordre 10 faisant intervenir 12 672 diagrammes de Feynman. La précision obtenue était alors inférieure au milliardième[28].
Interactions élémentaires[modifier | modifier le code]
Les diagrammes de Feynman permettent de décrire les trois interactions élémentaires, autres que la gravité.
Électrodynamique quantique[modifier | modifier le code]

Dans cette théorie, trois séquences de base permettent de générer tous les phénomènes physiques qui font intervenir de la lumière et des électrons[19] :
- un photon va d'un endroit à un autre ;
- un électron va d'un endroit à un autre ;
- un électron émet ou absorbe un photon.
Plus généralement, l'électrodynamique quantique traite des interactions entre les particules chargées (ce qui inclut les électrons et leurs antiparticules, les positrons) et le champ électromagnétique (dont les vecteurs de force sont les photons) ; dans les diagrammes de Feynman, l'électron est représenté avec une flèche qui va dans le sens du temps, le positron avec une flèche qui va dans le sens contraire, et le photon avec une ligne ondulée[Note 7],[30].
Les interactions entre ces trois particules se réduisent à un seul schéma de jonction, ou vertex, composé d'une flèche entrante, d'une flèche sortante et d'une connexion avec un photon. Selon l'orientation de ce vertex dans le temps on obtient six interactions possibles[31],[15] :
-
Un électron émet un photon :
-
Un électron absorbe un photon :
-
Un positron émet un photon :
-
Un positron absorbe un photon :
-
Un positron et un électron s'annihilent en un photon :
-
Un photon crée un électron et un positron :
Toutes les interactions entre particules chargées et lumière sont construites à partir de ces briques de base, et uniquement celles-ci, parce qu'elles suivent les lois de conservation, en particulier la conservation de l'énergie, la conservation de la quantité de mouvement (ou impulsion) et la conservation de la charge électrique. Toute interaction plus complexe est une combinaison de ces six vertex[32].
Chromodynamique quantique[modifier | modifier le code]
En 1968, Richard Feynman montre que ses diagrammes peuvent aussi s'appliquer à l'interaction forte, ils permettent donc de décrire la chromodynamique quantique en ajoutant de nouvelles règles. Le processus fondamental analogue à la réaction électron-photon de l'électrodynamique est alors la réaction quark-gluon, dans laquelle la charge de couleur est conservée (mais pas la saveur). Les gluons portant comme les quarks des charges de couleur (contrairement aux photons qui sont neutres) il existe des vertex impliquant uniquement des gluons[33] :
| Vertex de la chromodynamique quantique | |||||||||
| |||||||||
L'étude des interactions fortes avec les diagrammes de Feynman est possible grâce à la propriété de liberté asymptotique qui permet d'appliquer la théorie des perturbations aux quarks et aux gluons : à très faible distance cette interaction devient faible[34],[35]. On définit alors la constante de couplage de l'interaction forte pour un vertex, notée , équivalent de la constante de structure fine en électrodynamique quantique. La difficulté en chromodynamique quantique vient du fait que les quarks sont fortement influencés par les forces non perturbatives. En se plaçant à des niveaux d'impulsion très grands, où le couplage est faible, la valeur de obtenue permet de calculer le résultat de processus de diffusion à haute énergie[36].
Interaction faible[modifier | modifier le code]
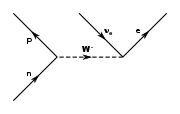
L'interaction faible fait intervenir ses trois bosons de jauge, le boson W dans ses deux états, et , ainsi que le boson [37]. Ces médiateurs sont généralement tracés avec une ligne en pointillés ou une ligne ondulée (la même que celle du photon) annotée avec la lettre du boson correspondant. La ligne droite fléchée s'étend ici aux quarks et aux autres leptons, accompagnée de leur symbole.
| Vertex de l'interaction électrofaible (sans symboles) | ||||||||||||
| ||||||||||||
Signification[modifier | modifier le code]
Les diagrammes de Feynman ne représentent pas des trajectoires de particules. Mathématiquement, ils sont un « moyen graphique de représenter le contenu du théorème de Wick »[13]. En effet, dans la quantification canonique de la théorie quantique des champs, un diagramme correspond à un terme de l'expansion de Wick dans le développement perturbatif de la matrice de diffusion.
Calcul de l'amplitude par des séries perturbatives[modifier | modifier le code]
Aucune méthode ne permet de calculer les solutions exactes des équations donnant l'état d'un système quantique, il faut donc recourir à des approximations appelées séries perturbatives. Les diagrammes de Feynman permettent de visualiser et d'organiser simplement les termes de ces séries[38].
La théorie permet de prédire des valeurs de sections efficaces ; ces valeurs sont comparées aux résultats d’expériences en physique des particules pour évaluer la fiabilité d’un modèle théorique donné. On utilise généralement la différentielle de cette section efficace, qui est fonction du module au carré de l'amplitude de diffusion, notée [39] :
- où est l'énergie supposée égale de chacun des deux faisceaux de particules qui ont participé à l'expérience.
Il n'existe généralement pas de formule permettant de calculer l'amplitude , mais des séries perturbatives peuvent en approcher la valeur[40].
Les diagrammes de Feynman sont une notation graphique de termes mathématiques utilisés pour réaliser ces calculs perturbatifs. Chaque diagramme représente un des termes algébriques d'une série perturbative[41]. Cette somme algébrique, décomposition perturbative d'une amplitude de diffusion, est équivalente à une série de diagrammes de Feynman. À chaque terme est ainsi associé un graphe qui propose un scénario en termes de particules, chaque scénario étant connecté à l'autre par ses lignes entrantes et sortantes[42]. Le passage d'une représentation à l'autre permet d'avancer le calcul par celle qui semble la plus simple ou la plus appropriée[43].
Un des premiers grands résultats de ces diagrammes est qu'ils donnaient un outil graphique pour calculer les éléments de la matrice de diffusion, dans la théorie des perturbations, à n'importe quel ordre[44].
Vertex[modifier | modifier le code]

La charge de l'électron est très petite : elle vaut dans des unités bien choisies[Note 8]. Quand on calcule la contribution d'interaction avec un seul photon elle est proportionnelle à , avec deux photons elle est proportionnelle à , avec trois c'est un facteur qui est environ 10 000 fois plus petit que . Même si cette idée semble éliminer très rapidement les contributions des interactions négligeables, leur calcul pratique est extrêmement compliqué : un étudiant de Werner Heisenberg a essayé de calculer une contribution à deux photons (en ), mais s'est retrouvé avec des centaines de termes[1].
Avec un diagramme de Feynman, la contribution d'un terme perturbatif est immédiate : un vertex apporte une contribution égale à , tous les termes peuvent alors être classés selon leur contribution, , , , etc[45]. Pour trouver la probabilité de changement d'état quantique du phénomène étudié, il ne reste plus qu'à calculer uniquement les termes nécessaires à la précision souhaitée en éliminant l'infinité des autres cas possibles[46].
Particules virtuelles[modifier | modifier le code]
Aux débuts de l'électrodynamique quantique, dans les années 1930, les calculs sur les cas les plus simples, comme connaître la probabilité de diffusion des deux électrons, donnait souvent des valeurs infinies : des approximations limitées étaient possibles, mais dès que l'on souhaitait trouver des valeurs plus précises on retombait sur des infinis. Cela vient du fait que les photons virtuels échangés dans cette interaction peuvent avoir une énergie très grande tant qu'elles l'utilisent sur un temps très court. En plus d'avoir des énergies illimitées, les particules virtuelles échangées ne sont pas non plus limitées en nombre : les équations algébriques nécessitent des termes mathématiques dont le nombre augmente exponentiellement avec celui des photons[47].
Le calcul de l'intégrale de chemin, qui donne la probabilité pour une particule quantique de passer d'un point à un autre, nécessite d'ajouter les contributions de tous les chemins possibles entre ces deux points, ainsi que celles des chemins impossibles[48]. Un calcul exact n'est pas réalisable parce qu'il faudrait faire la somme d'une infinité d'états intermédiaires[49]. Les diagrammes de Feynman permettent de trouver parmi cette infinité de possibilités la probabilité recherchée, et cela avec des règles extrêmement simples[50].
Propagateurs[modifier | modifier le code]
Dans les diagrammes de Feynman, les propagateurs sont les contributions des particules virtuelles. Leur nom vient du fait qu'ils décrivent la propagation de ces particules qui se déplacent librement sauf aux points d'émission ou d'absorption[51]. Richard Feynman a appliqué les fonctions de Green aux particules élémentaires sous la forme d'un opérateur particulier de la théorie quantique des champs qu'il a nommé propagateur[52].
Pour un boson libre, l'équation de Klein-Gordon donne l'équation de mouvement :
- où est une fonction d'onde scalaire.
Alors, la fonction de Green est solution, dans l'espace des impulsions, à l'équation :
- où est la distribution de Dirac, avec .
Ce qui s'écrit aussi :
- .
Feynman interprète comme l'amplitude de probabilité associée au boson se propageant avec le quadri-moment , qui vaut :
- .
De manière analogue, il définit un opérateur pour les vertex (émission ou absorption d'un boson), ce qui aboutit aux règles de Feynman permettant de calculer les amplitudes décrites par ses diagrammes[52].
Représentativité[modifier | modifier le code]

D'après le principe d'incertitude de Heisenberg, on ne peut attribuer une trajectoire à une particule. Niels Bohr l'interprète de manière radicale en affirmant qu'il est impossible de représenter des phénomènes quantiques[6]. Les diagrammes de Feynman semblent contredire cette assertion en montrant directement ce qui pourrait se passer au niveau atomique. L'analogie avec les traces laissées par les particules dans les chambres à bulles renforce cette idée[53]. Cependant, ces diagrammes ne représentent en aucun cas des événements physiques[54]. Ils peuvent même être trompeurs car contradictoires avec le phénomène qu'ils illustrent : dans la diffusion Bhabha par exemple, l'électron et le positron s'attirent l'un l'autre, alors que dans leur diagramme les lignes finissent par s'écarter et les particules semblent se repousser[27].
Du point de vue physique, un diagramme de Feynman correspond à une infinité d'événements, la somme de tous les chemins possibles et impossibles représentée par l'intégrale de chemin. De plus, il n'a pas d'échelle, ses points et ses lignes ne sont ni des particules ni des distances[54]. Du point de vue mathématique, les diagrammes utilisés en théorie quantique des champs représentent uniquement les termes d'une somme d'amplitudes de probabilité, des approximations dans une série perturbative. Un tel graphe correspond à des événements inobservables, appelés par les physiciens des « particules virtuelles »[55].
Richard Feynman mettait en garde contre une utilisation figurative de ses diagrammes. Il ne les considérait que comme une aide pour interpréter les équations de la théorie des champs[11]. Il leur trouvait d'ailleurs un air comique quand il a commencé à les dessiner, et ils n'avaient rien d'intuitif lorsqu'il les a présentés aux autres physiciens[56].
Cependant, leur succès tient au fait qu'ils forment une aide précieuse pour la visualisation et la manipulation des séries perturbatives, d'autant plus que chaque terme algébrique peut être traduit en diagramme de Feynman et inversement[42]. Julian Schwinger leur donnait ainsi des vertus pédagogiques et non physiques[57].
Si on simplifie au maximum, on peut dire que les diagrammes de Feynman montrent la diffusion des électrons et des photons sous une forme très abstraite. Mais la plupart des physiciens évitent d'utiliser cette analogie[58].
Ces diagrammes sont parfois confondus avec ceux de Minkowski, qui existaient avant ceux de Feynman, et qui décrivent intuitivement des propriétés de l'espace-temps dans la théorie de la relativité restreinte[59].
Règles de Feynman[modifier | modifier le code]
Les règles de Feynman traduisent directement un diagramme en une contribution de , elles font correspondre un facteur algébrique à chaque élément et le produit de ces facteurs donne la valeur de cette contribution (la somme des contributions donne une valeur approchée de )[40].
Pour les formules algébriques qui suivent, on se place dans le système d'unités naturelles où la constante de Planck réduite et la vitesse de la lumière sont des unités, et donc : .
Électrodynamique quantique[modifier | modifier le code]
Règles de Feynman pour calculer en électrodynamique quantique[60] :
| Catégorie | Symbole | Spin | Particule(s) | Facteur multiplicateur |
|---|---|---|---|---|
| Lignes externes | 0 | boson entrant | 1 | |
| 0 | boson sortant | 1 | ||
| 0 | antiboson entrant | 1 | ||
| 0 | antiboson sortant | 1 | ||
| ½ | fermion entrant | |||
| ½ | fermion sortant | |||
| ½ | antifermion entrant | |||
| ½ | antifermion sortant | |||
| 1 | photon entrant | |||
| 1 | photon sortant | |||
| Propagateurs (lignes internes) |
0 | boson | ||
| ½ | fermion | |||
| 1 | particule sans masse (photon) |
|||
| 1 | particule massive (boson) |
|||
| Vertex | 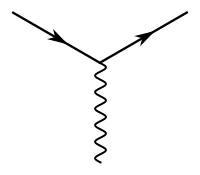
|
- où et sont les spineurs de Dirac, avec pour normalisé : ,
- le vecteur de polarisation circulaire du photon,
- la masse de la particule,
- l'unité imaginaire,
- pour le quadri-moment et la matrice de Dirac ,
- la métrique de Minkowski,
- la charge de l'électron.
Chromodynamique quantique[modifier | modifier le code]
Règles de Feynman en chromodynamique quantique[61] :
| Catégorie | Symbole | Particule(s) | Facteur multiplicateur |
|---|---|---|---|
| Lignes externes | quark entrant | ||
| quark sortant | |||
| antiquark entrant | |||
| antiquark sortant | |||
| gluon entrant | |||
| gluon sortant | |||
| Propagateurs | quark ou antiquark | ||
| gluon | |||
| Vertex | 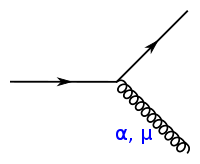
|
quark-gluon | |

|
3 gluons |
| |
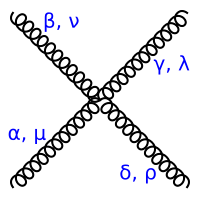
|
4 gluons |
|
Interaction faible[modifier | modifier le code]
Règles de Feynman pour l'interaction faible[62] :
| Catégorie | Symbole | Particule(s) | Facteur multiplicateur | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vertex | 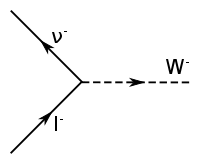
|
boson W−, un lepton et son neutrino | |||||||||||||||

|
qi est un quark up, charm ou top, qj un quark down, strange ou bottom |
(où U est la matrice CKM) | |||||||||||||||

|
boson Z0 et f un quark ou un lepton |
| |||||||||||||||
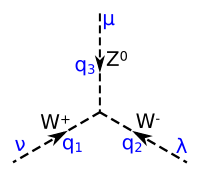
|
les 3 bosons |
| |||||||||||||||

|
les 2 bosons W et un photon |
| |||||||||||||||
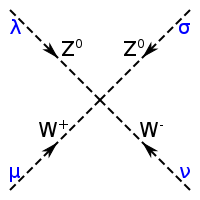
|
les 2 bosons W et 2 bosons Z | ||||||||||||||||

|
2 bosons W+ et 2 bosons W− | ||||||||||||||||

|
les 2 bosons W et 2 photons | ||||||||||||||||

|
les 2 bosons W, un boson Z et un photon |
Applications[modifier | modifier le code]
La plupart des propriétés connues des particules ont été déterminées par des expériences de diffusion[63]. Un des buts des diagrammes de Feynman est de calculer la section efficace théorique d'un phénomène pour la comparer aux valeurs expérimentales. Une fois les règles de Feynman établies, il suffit d'appliquer une recette à un processus physique donné pour en calculer l'amplitude : choisir les particules entrantes et sortantes, dessiner tous les diagrammes possibles jusqu'à la précision voulue, écrire les formules des amplitudes de chaque diagramme à partir des règles, sommer toutes ces formules pour obtenir l'amplitude du processus[64].
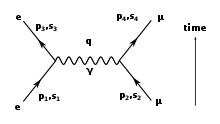
Réaction [modifier | modifier le code]

La réaction d'annihilation d'une paire électron-positron qui donne une paire muon-antimuon est la plus simple et la plus importante de l'électrodynamique quantique[65].
L'amplitude de transition de cette réaction s'écrit[66] :
- où est le facteur qui correspond aux lignes extérieures du diagramme pour le positron et l'électron,
- le facteur pour l'antimuon et le muon,
- sont les vertex (partie de l'interaction de l'opérateur hamiltonien),
- , l'opérateur de la ligne interne du photon.
En utilisant les règles de Feynman, on obtient[67] :
- où , , et sont les spineurs des lignes externes, avec , , , et leurs spins,
- et sont les vertex (),
- et correspond à la ligne du photon (opérateur ).
Diffusion Bhabha[modifier | modifier le code]
La diffusion Bhabha est un processus de diffusion entre une particule élémentaire et son antiparticule, soit un électron et un positron en électrodynamique quantique. Elle est décrite par deux diagrammes, l'un de diffusion classique et l'autre d'annihilation avec création de paires :
-
annihilation (canal s)
-
diffusion (canal t)
Les canaux et sont définis par les variables de Mandelstam[68]. Grâce aux règles de Feynman, on écrit pour chaque diagramme (et donc chaque canal) un élément de matrice[réf. souhaitée] :
- où et sont les quadri-moments du positron, et ceux de l'électron,
- et les spineurs du positron, et ceux de l'électron,
- sont les quatre matrices de Dirac.
Effet Compton[modifier | modifier le code]
L'effet Compton est la diffusion inélastique d'un photon par la matière. Les diagrammes suivants rendent compte des deux ordres possibles de l'absorption et de l'émission des photons[69] :
| Diffusion Compton | |||||||||
| |||||||||
Si on écrit cette diffusion avec le photon initial et le photon final, alors les règles de Feynman donnent pour les amplitudes des deux diagrammes[70] :
Diffusion Møller[modifier | modifier le code]
La diffusion Møller (en) décrit la diffusion de deux électrons : , et implique les canaux et de Mandelstam[68].
|
Décalage de Lamb[modifier | modifier le code]
Le décalage de Lamb représente l'écart entre les deux niveaux de structure fine de l'atome d'hydrogène notés et . Les trois premières contributions à ce décalage sont représentées par les diagrammes suivants, donnant dans l'ordre la renormalisation de la masse de l'électron, son moment magnétique anomal et la polarisation du vide, totalisant une différence de 1 058 MHz par opposition à l'équation de Dirac qui leur donne le même niveau[71] :
| Les trois premières contributions au décalage de Lamb | |||||||||
| |||||||||
Fluctuation quantique du vide[modifier | modifier le code]


Les photons émis puis réabsorbés par le même électron sont des photons virtuels dus à l'interaction avec les fluctuations quantiques du vide. Les diagrammes suivants représentent aussi la self-énergie de l'électron à plusieurs boucles[73] :
| Boucles de self-énergie | |||||||||
| |||||||||
Réaction hadrons[modifier | modifier le code]
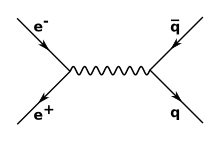
En chromodynamique quantique, l'annihilation électron-positron qui produit une paire de quarks comporte en première correction trois diagrammes différents, tous avec échange d'un gluon[74] :
| Corrections d'ordre α | |||||||||
| |||||||||
Critiques et autres théories[modifier | modifier le code]
Les diagrammes de Feynman ont permis de calculer les amplitudes de diffusion pendant plus de 60 ans, mais malgré leur efficacité, ils ne permettent pas de traiter des réactions compliquées : le nombre de termes nécessaires à l'ordre de correction supérieur augmente exponentiellement. La technique, dite « méthode d'unitarité », déjà utilisée dans les années 1960, a permis de dépasser ce problème[75]. En chromodynamique quantique, l'analyse de la diffusion de deux gluons qui en donne trois était trop complexe avec les diagrammes. Cette méthode donne une formule simple qui tient sur une page et permet de comprendre la réaction à l'aide du principe d'unitarité, principe implicite dans les diagrammes de Feynman car masqué par la complexité. Elle évite d'avoir recours aux particules virtuelles, la source même de la complexité des diagrammes : quand la méthode de Feynman ajoute tous les diagrammes possibles d'une réaction, y compris celles qui semblent impossibles, alors même qu'elles finissent par s'annuler, la méthode d'unitarité ne considère que les réactions utiles[76].
Autres utilisations[modifier | modifier le code]
Le formalisme des diagrammes de Feynman, que ce soit dans leur représentation graphique ou dans les idées mathématiques qui les sous-tendent, a été repris dans de nombreux domaines de la physique.
En physique nucléaire, les processus sont proches de ceux des interactions élémentaires. Les équations et les mesures sont analogues, puisque l'on calcule aussi des amplitudes pour vérifier les sections efficaces[77].
De même, en physique de la matière condensée dont le sous-domaine le plus important est la physique du solide, la description théorique utilise des entités appelées quasiparticules qui peuvent être décrites par des fonctions de Green et donc des propagateurs comme pour les particules élémentaires. Ces interactions sont ainsi calculées avec des diagrammes de Feynman[78].
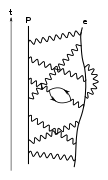
| Diagrammes pour d'autres physiques | |||||||||
| |||||||||
Références culturelles[modifier | modifier le code]
Richard Feynman achète en 1975 une camionnette, immatriculée QANTUM, sur laquelle il peint les diagrammes qu'il a inventés. Vendue par sa femme après sa mort, elle continue à rouler. Seamus Blackley la rachète en 2012 et refait les diagrammes effacés pour traverser les États-Unis avec une exposition itinérante organisée avec Edward Tufte et le Fermilab[79],[80].
Cette camionnette apparaît en 2015 dans le troisième épisode de la neuvième saison de la série télévisée The Big Bang Theory, intitulé Corrosion, Crevaison, Oxydation[81],[82]. Cette série, qui met en scène deux physiciens, fait de nombreuses références à Feynman et montre plusieurs fois ses diagrammes ; celui de la réaction électron-muon apparaît en particulier dans le treizième épisode de la première saison, La Conjecture du Batbocal, pour départager les deux équipes finalistes du concours de physique[83].
L'ingénieur en physique Andrew Charalambous a créé de nombreuses œuvres d'art représentant des diagrammes de Feynman, à la fois par passion et dans un but de vulgarisation[84],[85].
Les idées contenues dans les diagrammes, comme celle des antiparticules représentées par une flèche allant dans le sens inverse du temps, a inspiré plusieurs auteurs de fiction : le concept de causalité inversée justifié par les théories de Feynman apparaît dans le roman Temps de Stephen Baxter pour transmettre des messages vers le passé, ou dans le film Primer de Shane Carruth pour voyager dans le temps[86],[87].
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- « Like the silicon chip of more recent years, the Feynman diagram was bringing computation to the masses. »
- Cette présentation a eu lieu dans les monts Pocono et s'appelle donc la conférence Pocono (en).
- Deux livres ont été publiés en 1953, l'un au Japon (Umezawa) et l'autre en Russie (Akhiezer et Berestetskii), mais n'ont été traduits en anglais qu'en 1956 et 1957 respectivement.
- Dans Einführung in die Quantentheorie der Wellenfelder, paru en 1943.
- Historiquement, l'orientation du temps vers le haut venait du diagramme de Minkowski[12].
- Les amplitudes de probabilité sont des fonctions à valeurs complexes.
- Feynman a utilisé l'interprétation d'Ernst Stueckelberg pour représenter les positrons (et les autres antiparticules) comme des entités remontant le temps[29].
- Cette constante de couplage, qui donne , est la constante de structure fine.
Références[modifier | modifier le code]
- Kaiser 2005, p. 158.
- O’Dowd 2017, 3 secondes.
- Rosenbaum 2009, p. 151-152.
- Wüthrich 2011, p. 1.
- Kaiser 2005, p. 9.
- Rosenbaum 2009, p. 152.
- Wüthrich 2011, p. 5.
- Kaiser 2005, p. 17.
- Kaiser 2005, p. 27.
- Kaiser 2005, p. 161.
- Rosenbaum 2009, p. 157.
- Kaiser 2005, p. 363.
- Martin et Rothen 1990, p. 323.
- Peskin et Schroeder 1995, p. 3.
- Marleau 2017, p. 79.
- Peskin et Schroeder 1995, p. 716.
- Baglio et Djouadi 2011, p. 5-7.
- Marleau 2017, p. 315.
- Feynman 1992, p. 119.
- Feynman 1992, p. 120.
- Griffiths 2004, p. 57.
- Feynman 1992, p. 126.
- Marleau 2017, p. 81.
- O’Dowd 2017, 5 min 25 s.
- Taillet, Villain et Febvre 2013, entrée « couche de masse », p. 152.
- O’Dowd 2017, 5 min 58 s.
- Griffiths 2004, p. 59.
- (en) Tatsumi Aoyama, Masashi Hayakawa, Toichiro Kinoshita et Makiko Nio, « Tenth-Order QED Contribution to the Electron g – 2 and an Improved Value of the Fine Structure Constant », Physical Review Letters, vol. 109, nos 11-14, , p. 4 (DOI 10.1103/PhysRevLett.109.111807, arXiv 1205.5368)
- Feynman 1949, p. 753.
- O’Dowd 2017, 2 min 2 s.
- O’Dowd 2017, 2 min 59 s.
- O’Dowd 2017, 4 min 30 s.
- Griffiths 2004, p. 61.
- Peskin et Schroeder 1995, p. 548.
- Kaiser 2005, p. 374.
- Peskin et Schroeder 1995, p. 551.
- Griffiths 2004, p. 301.
- Wüthrich 2011, p. 2.
- Peskin et Schroeder 1995, p. 4.
- Peskin et Schroeder 1995, p. 5.
- Rosenbaum 2009, p. 158.
- Rosenbaum 2009, p. 159.
- Rosenbaum 2009, p. 162.
- Wüthrich 2011, p. 16.
- Kaiser 2005, p. 160.
- O’Dowd 2017, 1 min 28 s.
- Kaiser 2005, p. 157.
- O’Dowd 2017, 25 secondes.
- O’Dowd 2017, 57 secondes.
- O’Dowd 2017, 1 min 12 s.
- Marleau 2017, p. 19.
- Marleau 2017, p. 20.
- Rosenbaum 2009, p. 153.
- Rosenbaum 2009, p. 154.
- Rosenbaum 2009, p. 155.
- Kaiser 2005, p. 51.
- Rosenbaum 2009, p. 160.
- Wüthrich 2011, p. 3.
- Rosenbaum 2009, p. 156.
- Griffiths 2004, p. 380.
- Griffiths 2004, p. 283.
- Griffiths 2004, p. 381.
- Marleau 2017, p. 59.
- Marleau 2017, p. 80-81.
- Peskin et Schroeder 1995, p. 131.
- Peskin et Schroeder 1995, p. 6.
- Peskin et Schroeder 1995, p. 10.
- Peskin et Schroeder 1995, p. 157.
- Marleau 2017, p. 45.
- Marleau 2017, p. 131.
- Jean-Christophe Pain, « Willis Eugene Lamb (1913–2008) La passion de la précision », Reflets de la physique, no 36, , p. 27-29 (DOI 10.1051/refdp/201336027, lire en ligne).
- Peskin et Schroeder 1995, p. 336.
- Marleau 2017, p. 23.
- Peskin et Schroeder 1995, p. 549.
- Bern, Dixon et Kosower 2012, p. 36.
- Bern, Dixon et Kosower 2012, p. 39.
- Blokhintsev 2003.
- Mattuck 1992, p. 12.
- (en) Ralph Leighton, « The Feynman Van », sur feynman.com (consulté le ).
- (en) Kathryn Jepsen, « Saving the Feynman van », sur symmetrymagazine.org, (consulté le ).
- (en) « The Bachelor Party Corrosion », sur bigbangtheory.wikia.com (consulté le ).
- (en) « CHUCK LORRE PRODUCTIONS, #503 », sur chucklorre.com (consulté le ).
- (en) « Richard Feynman », sur bigbangtheory.wikia.com (consulté le ).
- (en) Katherine Wright, « Arts & Culture: Feynman for All », Physics, APS, (consulté le )
- (en) Andrew Charalambous, « Feynman inspired art » [PDF], sur cds.cern.ch, (consulté le ).
- (en) « Time Radio », sur sf-encyclopedia.com, (consulté le ).
- (en) Grant Watson, « “The answer was unknowable” », sur fictionmachine.com, (consulté le ).
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
Ouvrages et articles[modifier | modifier le code]
- (en) Julien Baglio et Abdelhak Djouadi, « Higgs production at the lHC » [« Production de Higgs au lHC »], Journal of High Energy Physics, (DOI 10.1007/JHEP03(2011)055, arXiv 1012.0530, lire en ligne, consulté le ).
 .
. - (en) Zvi Bern, Lance J. Dixon et David A. Kosower, « Loops, Trees and the Search for New Physics » [« Boucles et arbres, à la recherche d'une nouvelle physique »], Scientific American, vol. 306, no 5, (DOI 10.1038/scientificamerican0512-34, lire en ligne [PDF], consulté le ).
 .
. - (en) L. D. Blokhintsev, « Feynman diagrams in nuclear physics at low and intermediate energies », Selected topics in theoretical physics and astrophysics, , p. 99-104 (lire en ligne [PDF]).
 .
. - Richard Feynman (trad. Françoise Balibar, Alain Laverne), Lumière et matière : Une étrange histoire [« QED, The Strange Theory of Light and Matter »], InterÉditions, coll. « Sciences », (1re éd. 1987), 206 p. (ISBN 978-2-02-014758-3).

- (en) Richard Feynman, « The Theory of Positrons », Physical Review, vol. 76, no 6, , p. 749-759 (lire en ligne, consulté le ).
- (en) David Griffiths, Introduction to Elementary Particles, Wiley-VCH, , 402 p. (ISBN 978-0-471-60386-3).

- (en) Gerard 't Hooft et Martinus Veltman, Diagrammar, Genève, CERN, , 119 p. (lire en ligne).
- (en) David Kaiser, Drawing Theories Apart : The Dispersion of Feynman Diagrams in Postwar Physics, Chicago, University of Chicago Press, , 490 p. (ISBN 0-226-42266-6).

- (en) David Kaiser, « Physics and Feynman’s Diagrams », American Scientist, vol. 93, , p. 156-165 (lire en ligne, consulté le ).

- Luc Marleau, Introduction à la physique des particules, Université Laval, Québec, Canada, , 413 p. (lire en ligne).

- Philippe A. Martin et François Rothen, Problèmes à N-corps et champs quantiques, Lausanne, Presses polytechniques et universitaires romandes, coll. « Physique », , 387 p. (ISBN 2-88074-193-9, lire en ligne).
 .
. - (en) Richard D. Mattuck, A guide to Feynman diagrams in the many-body problem, New York, Dover, (1re éd. 1967), 464 p. (ISBN 978-0-486-67047-8, lire en ligne).

- (en) Michael E. Peskin et Daniel V. Schroeder, An Introduction to Quantum Field Theory, Reading (Massachusetts), Perseus Books, coll. « The Advanced Book Program », , 862 p. (ISBN 0-201-50397-2).

- Alexis Rosenbaum, « Sur le statut des diagrammes de Feynman en théorie quantique des champs », Philosophia Scientiæ, vol. 13, no 2, , p. 151-166 (DOI 10.4000/philosophiascientiae.301).

- Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Paris, De Boeck Supérieur, , 899 p. (ISBN 978-2-8041-7554-2, lire en ligne), p. 189.

- (en) Martinus Veltman, Diagrammatica : the path to Feynman diagrams, Cambridge Lecture Notes in Physics, (ISBN 0-521-45692-4)
- (en) Adrian Wüthrich, The Genesis of Feynman Diagrams, vol. 26, Springer Netherlands, coll. « Archimedes », , 228 p. (ISBN 978-90-481-9227-4).

- (en) Anthony Zee, Quantum Field Theory in a Nutshell, Princeton University Press, coll. « In a Nutshell », , 576 p. (ISBN 978-0-691-14034-6, lire en ligne).
Conférences et vidéos[modifier | modifier le code]
- Les diagrammes de Feynman, la partition du modèle standard, (MP3, MP4, MOV, WMV), Gilles Cohen-Tannoudji (physicien) () École normale supérieure (Paris) : Collectif Histoire Philosophie Sciences. Consulté le .
- (en) Solving the Impossible in Quantum Field Theory, (YouTube), Matt O’Dowd () PBS Space Time. Consulté le .
- (en) The Secrets of Feynman Diagrams, (YouTube), Matt O’Dowd () PBS Space Time. Consulté le .

Article connexe[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- [vidéo] (en) Dr. Don Lincoln, « Feynman diagrams », sur YouTube, Fermilab, (consulté le ).
- (en) JaxoDraw : logiciel de dessin de diagrammes de Feynman
- (en) Outil en ligne de dessin de diagrammes de Feynman
























































































![{\displaystyle g_{\lambda \mu }(k_{3}-k_{1})_{\nu }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9181fd9d1e269f3c7c8e638654c542eb46d63462)


![{\displaystyle f^{\alpha \gamma \eta }f^{\delta \beta \eta }(g_{\mu \rho }g_{\nu \lambda }-g_{\mu \nu }g_{\lambda \rho })]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90a5db0688e897aba5e329540010cb587a431a03)























![{\displaystyle g_{\mu \nu }(q_{3}-q_{1})_{\lambda }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0489925e1cdc4f3eeb395050698deab5a821027)