Méthode de dichotomie
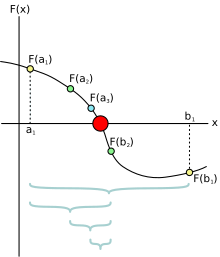
La méthode de dichotomie ou méthode de la bissection est, en mathématiques, un algorithme de recherche d'un zéro d'une fonction qui consiste à répéter des partages d’un intervalle en deux parties puis à sélectionner le sous-intervalle dans lequel existe un zéro de la fonction.
Principe[modifier | modifier le code]
On considère deux nombres réels a et b et une fonction réelle f continue sur l'intervalle [a, b] telle que f(a) et f(b) soient de signes opposés. Supposons que nous voulions résoudre l'équation f(x) = 0. D'après le théorème des valeurs intermédiaires, f a au moins un zéro dans l’intervalle [a, b]. La méthode de dichotomie consiste à diviser l’intervalle en deux en calculant m = (a+b)2. Il y a maintenant deux possibilités : soit f(a) et f(m) sont de signes contraires, soit f(m) et f(b) sont de signes contraires.
L’algorithme de dichotomie est alors appliqué au sous-intervalle dans lequel le changement de signe se produit, ce qui signifie que l’algorithme de dichotomie est récursif.
L’erreur absolue de la méthode de dichotomie est au plus
après n étapes car l'erreur est diminuée de moitié à chaque étape.
Réciproquement, si l'on cherche à ce que l'erreur absolue soit inférieure à une certaine valeur ε, on sait dénombrer le nombre d'itérations nécessaires N pour satisfaire cette tolérance sur le résultat final :
La méthode converge linéairement, ce qui est très lent par comparaison avec la méthode de Newton. L'avantage par rapport à cette dernière est son domaine d'application plus vaste : il suffit seulement que f(a) et f(b) soient de signes opposés et qu'on puisse déterminer le signe de f(m) à chaque itération.
Programmation[modifier | modifier le code]
Sous l'hypothèse que le signe de f(m) soit déterminable, voici une représentation de la méthode en pseudo-code, où ε est la précision souhaitée.
Tant que (b - a) > ε
m ← (a + b) / 2
Si (f(a)*f(m) ≤ 0) alors
b ← m
sinon
a ← m
Fin Si
Fin Tant que
Limite de la méthode[modifier | modifier le code]
Le principal avantage pratique de cette méthode est sa robustesse, puisque si f est continue, alors l'algorithme est théoriquement convergent (la taille de l'intervalle de recherche tend vers zéro). Le principal défaut de l'algorithme est que seul le signe de f est utilisé, ce qui mène à une convergence plutôt lente (convergence quasiment linéaire). La méthode de Newton, qui utilise la valeur de f ainsi que la valeur de la pente de f, est, quand elle converge, significativement plus rapide (convergence quadratique).
Par exemple, supposons que le zéro, simple, est égal à 1, que la fonction est deux fois continûment différentiable et que f'(x) = 1. Supposons, de plus qu'on utilise des nombres à virgule flottante binaire de type IEEE-754 avec 64 bits, dont 53 bits de précision. Supposons qu'on recherche une erreur absolue inférieure à 10-16. Si l'intervalle de recherche initial est de longueur égale à 1, alors la dichotomie nécessite 52 itérations. Au contraire, si le point initial est associé à une erreur absolue inférieure à 0,1, alors la méthode de Newton converge en seulement 5 itérations.
Cette méthode d'une grande robustesse nécessite cependant de connaître à chaque étape le signe de f(m). Dans quelques cas, il peut arriver que la valeur de f(m) soit si proche de 0 que la précision du logiciel de calcul ne permette plus de déterminer le signe de f(m) (les erreurs d'arrondi peuvent conduire au signe opposé, ou à 0). L'application de l'algorithme risque alors de conduire à l'élimination erronée d'une moitié de l'intervalle et à la convergence vers une valeur éloignée de la racine.
D'une manière plus générale, la détermination du signe de f(m) peut se révéler impossible, même en augmentant la précision du calcul du logiciel. Considérons par exemple un réel α dont on peut calculer des valeurs approchées décimales ou rationnelles αn à toute précision 1n désirée. Considérons maintenant la fonction f affine sur les intervalles [0 , 13], [13 , 23] et [23 , 1] et telle que f(0) = -1, f(1) = 1, f(13) = f(23) = α. La méthode de dichotomie demande de déterminer le signe de f(12) = α. Or il n'existe aucun algorithme général permettant de décider si α > 0, α = 0 ou α < 0. En effet, un tel algorithme, s'il existait, ne devant effectuer qu'un nombre fini de calculs, devrait prendre sa décision au vu d'un nombre fini de valeurs approchées αn, ce qui est insuffisant pour conclure.
Cette limite conduit les théoriciens[1] de l'analyse constructive à qualifier la méthode de dichotomie de non constructive et à privilégier l'énoncé alternatif : rechercher une valeur x telle que |f(x)| soit inférieur à une erreur donnée.
Notes et références[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bisection method » (voir la liste des auteurs).
- (en) Richard L. Burden et J. Douglas Faires, Numerical Analysis, 7e éd., Brooks/Cole, 2000 (ISBN 0-534-38216-9)
- (en) Errett Bishop (en) et Douglas Bridges, Constructive Analysis, Springer-Verlag, 1985, p. 8.


