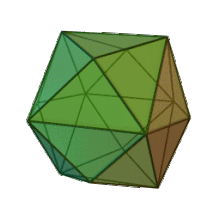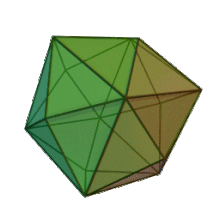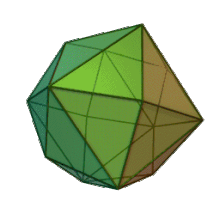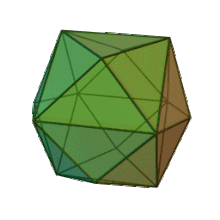
Tétrakihexaèdre
| Faces | Arêtes | Sommets |
|---|---|---|
| 24 triangles isocèles | 36 | 14 de degré 4 et 6 |
| Type | Solide de Catalan |
|---|---|
| Caractéristique | 2 |
| Propriétés | Convexe, uniformité des faces |
| Groupe de symétrie | Octaédrique |
| Dual | Octaèdre tronqué |
Un tétrakihexaèdre est un solide de Catalan (le dual d'un solide d'Archimède). Son dual est l'octaèdre tronqué.
Il peut être vu comme un cube dont chaque face (de côté a) est couverte par une pyramide carrée (de hauteur a/4). Cette interprétation est exprimée dans le nom, d'origine grecque : εξάεδρο / exáedro = « hexaèdre » (six faces) = cube, τετράκις / tetrákis = « quatre fois » = faces partagées en 4).
Longueurs, surface et volume[modifier | modifier le code]
Le rapport entre les longueurs des deux types d'arêtes est de 3/4.
Si la grande arête (celle du squelette cubique) a pour longueur a :
Son volume vaut :
Sa surface vaut :
Si l'on agrandit les pyramides de telle sorte que tous les triangles deviennent équilatéraux, le polyèdre devient un solide de Johnson ; il n'est plus convexe ni inscriptible dans une sphère. Toutes ses arêtes sont alors de longueur a.
Le volume devient :
La surface devient :
Applications humaines et naturelles[modifier | modifier le code]
Des dés polyédriques ayant la forme de tétrakihexaèdres sont occasionnellement utilisés par des joueurs.
Des formations cristallines naturelles de tétrakihexaèdres sont observées dans le cuivre et la fluorine.
Références[modifier | modifier le code]
- Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, (ISBN 0-486-23729-X)
- Sur le site Mathworld
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- (en) Les polyèdres uniformes
- (en) Les polyèdres en réalité virtuelle L'encyclopédie des Polyèdres.
- (en) Patrons en papier de polyèdres