Dérivée
En mathématiques, la dérivée d'une fonction d'une variable réelle mesure l'ampleur du changement de la valeur de la fonction (valeur de sortie) par rapport à un petit changement de son argument (valeur d'entrée). Les calculs de dérivées sont un outil fondamental du calcul infinitésimal. Par exemple, la dérivée de la position d'un objet en mouvement par rapport au temps est la vitesse (instantanée) de l'objet.
La dérivée d'une fonction est une fonction qui, à tout nombre pour lequel admet un nombre dérivé, associe ce nombre dérivé. La dérivée en un point d'une fonction de plusieurs variables réelles, ou à valeurs vectorielles, est plus couramment appelée différentielle de la fonction en ce point et n'est pas traitée ici.
La dérivée d'une fonction en est usuellement notée ou .
On utilise aussi des notations spécifiques, en particulier en physique, pour désigner la dérivée par rapport au temps qui s'écrit avec un point surmontant la lettre (), la dérivée seconde s'écrivant alors grâce à un tréma surmontant la lettre. Cette notation est appelée « notation de Newton ». On utilise dans le même esprit les notations prime () et seconde () pour noter les dérivées par rapport à l'espace.
En analyse, le nombre dérivé en un « point » (réel) d'une fonction à variable et valeurs réelles est la pente de la tangente au graphe de au point . C'est le coefficient directeur de l'approximation affine de en ; ce nombre n'est donc défini que si cette tangente — ou cette approximation — existe. La notion de dérivée est une notion fondamentale en analyse permettant d'étudier les variations d'une fonction, de construire des tangentes à une courbe et de résoudre des problèmes d'optimisation.
En sciences, lorsqu'une grandeur est fonction du temps, la dérivée de cette grandeur donne la vitesse instantanée de variation de cette grandeur, et la dérivée de la dérivée donne l'accélération. Par exemple, la vitesse instantanée d'un mobile est la valeur à cet instant de la dérivée de sa position par rapport au temps, et son accélération est la valeur à cet instant de la dérivée, par rapport au temps, de sa vitesse.
On généralise la notion de dérivée en étendant celle-ci au champ complexe et on parle alors de dérivée complexe. Pour une fonction de plusieurs variables réelles, on parle de la dérivée partielle par rapport à l'une de ses variables.
Il existe aussi une définition purement algébrique de la dérivée. On en trouve un exemple dans l'article polynôme formel.
Histoire[modifier | modifier le code]
Sa création est liée à une polémique entre deux mathématiciens : Isaac Newton et Gottfried Wilhelm Leibniz. Néanmoins, on retrouve chez des mathématiciens plus anciens les prémices de ce type de calcul : Pierre de Fermat et Isaac Barrow notamment. L'histoire du calcul infinitésimal remonte même à l'Antiquité, avec Archimède.
La notion de nombre dérivé a vu le jour au XVIIe siècle dans les écrits de Leibniz et ceux de Newton, qui le nomme fluxion et qui le définit comme « le quotient ultime de deux accroissements évanescents ». C'est à Lagrange (fin du XVIIIe siècle) que l'on doit la notation , aujourd'hui usuelle, pour désigner le nombre dérivé de en . C'est aussi à lui qu'on doit le nom de « dérivée » pour désigner ce concept mathématique.
Approche à partir de la pente de la tangente[modifier | modifier le code]

Pour approcher cette notion de manière graphique, commençons par nous donner une courbe représentative d'une fonction continue dans un repère cartésien, c'est-à-dire tracée d'un seul trait de crayon, et bien « lisse » ; on dira là que la fonction associée est dérivable.
Quel que soit le point que l'on choisit sur la courbe, on pourra alors tracer ce qu'on appelle une tangente, c'est-à-dire une droite qui épouse localement la direction de cette courbe. Si l'on trace la courbe et sa tangente et que l'on s'approche en zoomant suffisamment, on aura de plus en plus de mal à distinguer la courbe de sa tangente. Si la courbe « monte » (c'est-à-dire si la fonction associée est croissante), la tangente sera également montante ; inversement, si la fonction est décroissante, la tangente sera descendante.
Si on se donne une abscisse pour laquelle la fonction est dérivable, on appelle nombre dérivé de en le coefficient directeur de la tangente à la courbe au point d'abscisse . Ce réel donne de précieuses informations sur le comportement local d'une fonction : c'est la mesure algébrique de la vitesse à laquelle cette fonction change lorsque sa variable change.
Ainsi, si le nombre dérivé d'une fonction est positif sur un intervalle, cette fonction sera croissante sur ce même intervalle. Inversement, s'il est négatif, elle sera décroissante. Lorsque le nombre dérivé est nul en un point, la courbe admet une tangente horizontale en ce point (pour plus de détails, voir Fonction monotone#Monotonie et signe de la dérivée). Si de plus le nombre dérivé change de signe en ce point, alors la fonction admet un extremum local (minimum ou maximum) ; sinon, on obtient ce qu'on appelle un point d'inflexion et ainsi la courbe change de concavité.
Définition formelle[modifier | modifier le code]
Soit une fonction réelle à valeurs réelles définie sur une réunion quelconque d'intervalles non triviaux (c'est-à-dire non vides et non réduits à un point), et appartenant à l'intérieur de l'ensemble de définition .
Pour tout tel que , on appelle taux d'accroissement de en et avec un pas de la quantité :
Il s'agit du coefficient directeur de la droite reliant les points de coordonnées et .
Si admet une limite finie lorsque tend vers 0, on dit que est dérivable en , auquel cas le nombre dérivé de en est égal à la limite de ce taux d'accroissement. On note alors :
ou, de manière équivalente :
Une fonction pour laquelle le taux d'accroissement en un point admet une limite finie (qui est le nombre dérivé) est dite dérivable en ce point.
Ce calcul de limite revient graphiquement à rechercher la pente de la tangente à la courbe en ce point. Ainsi, le nombre dérivé d'une fonction en un point, s'il existe, est égal à la pente de la tangente à la courbe représentative de la fonction en ce point :

La dérivation peut aussi être définie pour des fonctions d'une variable réelle à valeurs dans d'autres ensembles que .
Par exemple, une fonction d'une variable réelle, à valeurs dans , est dérivable en si et seulement si toutes ses coordonnées sont dérivables en ; et sa dérivée est la fonction dont les coordonnées sont les dérivées des coordonnées de . C'est un cas particulier de fonctions d'une variable vectorielle et à valeurs dans un espace vectoriel normé ou métrique.
Dérivabilité et lien avec la continuité[modifier | modifier le code]
Typiquement, une fonction est dérivable si elle ne présente pas « d'aspérité », de rupture de pente ni de partie « verticale ».

Une fonction qui n'est pas continue en un point n'y est pas dérivable. Prenons l'exemple d'une fonction qui fait un saut. On ne peut pas définir de tangente, la limite du taux de variation est infinie (la pente de la courbe est verticale). C'est le cas par exemple de la fonction signe en 0 :
- à gauche de 0, i.e. , ;
- en 0 : ;
- à droite de 0, i.e. , ;
le taux de variation pour une largeur , vaut donc
et tend vers quand tend vers 0. Par contre, on peut définir une dérivée à gauche — dérivée partout nulle (tangente horizontale) sur — et une dérivée à droite — dérivée également nulle sur .


Si une fonction est dérivable en un point alors elle est continue en ce point, mais la réciproque est fausse.
Par exemple : la fonction valeur absolue est continue mais n'est pas dérivable en 0 :
- à gauche de 0, i.e. , la pente vaut ;
- à droite de 0, i.e. , la pente vaut .
Il y a une tangente à gauche et une tangente à droite différentes, la pente en 0 n'est pas définie ; le taux de variation n'a pas de limite définie. C'est le cas général pour les courbes présentant un point anguleux.
Il en est de même de la fonction racine cubique, qui a une tangente verticale en : le taux de variation a une limite infinie.
De plus, une fonction continue en un ensemble ne garantit pas que la fonction soit dérivable en cet ensemble (ouvert), comme contre-exemple la fonction de Weierstrass est continue sur mais dérivable nulle part.
Fonction dérivée[modifier | modifier le code]
La dérivabilité est a priori une notion locale (dérivabilité en un point), mais à toute fonction on peut associer sa fonction dérivée (prononcée « prime »), donnée par
où est le domaine de dérivabilité de (le sous-ensemble de constitué des points en lesquels est dérivable).
Les fonctions dérivées sont utilisées notamment dans l'étude des fonctions réelles et de leurs variations.
La seule fonction (à une constante multiplicative près) égale à sa dérivée — c'est-à-dire solution de l'équation différentielle — est la fonction exponentielle de base . Certains ouvrages[Lesquels ?] prennent cette propriété, avec la condition , comme définition de l'exponentielle.
Notations[modifier | modifier le code]
Il existe différentes notations pour exprimer la valeur de la dérivée d'une fonction en un point . On distingue :
- la notation de Lagrange[1] : ;
- la notation de Leibniz : ou . En physique, on note parfois . Cette dernière notation n'est pas rigoureuse car est un nombre constant, qui peut être vu comme une fonction constante : rigoureusement, on a donc ;
- la notation de Newton[2] : qui est plutôt utilisée en physique pour désigner une dérivée par rapport au temps (on parle alors de calcul des fluxions) ;
- la notation d'Euler : .
Ces notations permettent également d'écrire des dérivées itérées, cela se fait en multipliant le prime ou le point dans la notation (par exemple une dérivée seconde peut s'écrire ou ).
Dérivées usuelles et règles de dérivation[modifier | modifier le code]
peut souvent se calculer directement à partir d'une expression de , lorsqu'il s'agit d'une fonction « simple », en utilisant la table des dérivées usuelles. Pour des fonctions qui s'expriment comme combinaison linéaire de fonctions simples, comme produit, quotient ou composée, on utilise un petit nombre de règles algébriques déduites de la définition donnée plus haut. Les règles les plus couramment utilisées sont les suivantes :
| Nom | Règle | Conditions |
|---|---|---|
| Linéarité | Quels que soient le réel et les fonctions dérivables et . | |
| Produit | Quelles que soient les fonctions dérivables et . | |
| Inverse | Quelle que soit la fonction dérivable qui ne s'annule pas
(cas particulier de la ligne suivante) | |
| Quotient | Quelles que soient la fonction dérivable et la fonction dérivable qui ne s'annule pas | |
| Composée | Quelles que soient les fonctions dérivables (et composables) et | |
| Réciproque | Quelle que soit la fonction bijective de réciproque , dérivable de dérivée ne s'annulant en aucun point |
En particulier, voici les règles courantes se déduisant de la dérivée de composées :
| Nom | Règle | Conditions |
|---|---|---|
| Puissance | Quel que soit , et même quel que soit si | |
| Racine | Quelle que soit la fonction dérivable strictement positive
(cas particulier de la ligne précédente) | |
| Exponentielle | Quelle que soit dérivable | |
| Logarithme | Quelle que soit la fonction dérivable strictement positive | |
| Logarithme népérien | Quelle que soit la fonction dérivable strictement positive (cas de la ligne précédente) |
Dérivation numérique[modifier | modifier le code]
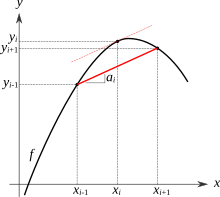
Dans le cas d'une courbe expérimentale, on ne possède pas de fonction explicite pour la décrire, mais une série de valeurs . On a donc recours à une dérivation numérique, qui consiste simplement à approcher la valeur de la dérivée en un point par le taux de variation entre les points précédent et suivant :
Graphiquement, cela revient à remplacer la tangente par la corde. Ceci peut se justifier par le théorème des accroissements finis : on sait qu'il existe un point de l'intervalle pour lequel la dérivée est la pente de la corde, et si l'intervalle est petit, alors ce point est proche du milieu . Cette méthode est automatisable sur les calculatrices programmables et les ordinateurs.
Il faut cependant se poser la question de la précision des résultats. Une mise en informatique « naïve » de la méthode de calcul peut mener à des résultats de précision médiocre dans certains cas.
Dans un ordinateur, la précision des nombres est limitée par le mode de représentation. Si l'on utilise la double précision selon la norme IEEE 754, les nombres ont environ 16 chiffres significatifs. On a donc une précision relative de l'ordre de 10−16 (2−52 exactement). Notons cette valeur. Les calculatrices de poche admettent typiquement 10 chiffres significatifs, soit = 10−10.
Supposons que la différence soit inférieure à , alors le calculateur fera une erreur grossière sur le calcul et le résultat sera médiocre ; voire, si la différence est très faible, il ne « verra pas » de différence entre les deux valeurs, et le résultat sera 0. Si par exemple on veut avoir la dérivée autour de 2 de la fonction , en prenant un écart de 10−13 entre les points :
- = 1,999 999 999 999 9
- = 2
- = 2,000 000 000 000 1
- ≈ 8 × 10−13
On voit que la différence entre les nombres, 8 × 10−13, est proche de . On va donc avoir une erreur d'arrondi. De fait, le calcul nous donne sur un ordinateur
- ≈ 3,997
alors que le résultat exact est
- = 2 × 21 = 4
soit une erreur de 0,3 %. Sur une calculatrice, le résultat est ≈ 0…
Le point critique est le choix de l'écart entre les valeurs de . Une valeur de l'ordre de convient dans de nombreux cas. Il nous manque encore quelques éléments pour cette étude ; le problème est abordé dans la section Précision de la dérivée numérique ci-dessous.
Donc :
- pour un ordinateur calculant en double précision, on peut prendre un écart de 10−8 entre les points ;
- pour une calculatrice avec 10 chiffres significatifs, on peut prendre un écart de 10−5 entre les points.
Précision de la dérivée numérique[modifier | modifier le code]
On peut approcher une fonction de classe C2 par un polynôme appelé développement limité[3] :
- .
Il en vient une approximation de la dérivée à l'ordre 2 :
- .
Ce faisant, on commet une erreur de troncature du second ordre
- .
Par ailleurs, l'ordinateur commet une erreur d'arrondi : la précision relative étant , la précision absolue sur est , et donc l'erreur induite sur la dérivée
- .
L'erreur totale vaut donc
- .
Cette fonction est convexe, et admet un minimum en
- .
Cela dépend donc du rapport entre la valeur de et la courbure . Pour les zones où la fonction est « modérée » — c'est-à-dire que est de l'ordre de l'unité —, on peut retenir
- .
L'erreur commise sur le premier terme (« erreur de méthode ») est en fait bien plus petite, puisque la méthode du paragraphe précédent revient à approximer par ; le même développement limité (pris cette fois à l'ordre 3) montre qu'on commet alors une erreur de l'ordre de . Il en résulte que le principal défaut de ces méthodes d'approximation numérique vient des erreurs d'arrondi.
Des formules plus complexes donnent de meilleures approximations ; voir à ce sujet l’article Dérivation numérique.
Dérivation graphique[modifier | modifier le code]

On peut également effectuer une dérivation graphique, sans utiliser de calcul. On approche les tangentes par les cordes comme pour la méthode numérique. Puis, on tire des parallèles à ces droites passant par un point nommé pôle P. On considère l'intersection de ces droites avec la verticale passant par O, le segment [OP] étant horizontal. La hauteur des segments ainsi délimités est proportionnelle à la pente :
on peut donc reporter cette hauteur sur le graphique et obtenir une approximation de la courbe dérivée. L'échelle de l'axe des est donc de OP:1.
Dérivée d'ordre n[modifier | modifier le code]
La dérivée seconde, notée , est la dérivée de la dérivée de , lorsqu'elle existe :
et la dérivée troisième est la dérivée de la dérivée seconde, lorsqu'elle existe :
- .
De manière générale, on définit la dérivée d'ordre pour une fonction fois dérivable par récurrence :
est également notée .
Formule de Leibniz[modifier | modifier le code]
Si et sont des fonctions fois dérivables, alors, par application de la règle du produit :
- .
En particulier pour ,
On notera l'analogie avec la formule du binôme de Newton. Cela provient de la bilinéarité de l'opérateur de dérivation d'un produit.
Propriétés des fonctions dérivables[modifier | modifier le code]
Théorème de Rolle[modifier | modifier le code]
Soient et deux réels tels que . Si est continue sur , dérivable sur , et si , alors il existe (au moins) un réel dans tel que :
- .
Théorème des accroissements finis[modifier | modifier le code]
- Énoncé
- Si une fonction est continue sur , avec , et dérivable sur , alors il existe un point de tel que le nombre dérivé de en ce point soit le taux de variation entre et
- .
En particulier, si , on retrouve le théorème de Rolle, qui sert aussi à démontrer le résultat plus général (voir l'article détaillé), c'est pourquoi on le rencontre souvent sous le nom de lemme de Rolle.
Cette propriété est utilisée en cinématique pour déterminer une approximation du vecteur vitesse à partir d'un relevé de point.
Discontinuités[modifier | modifier le code]
Une partie d'un intervalle réel est l'ensemble des points de continuité de la dérivée d'une fonction dérivable de dans si et seulement si[4] est un ensemble Gδ dense dans .
L'ensemble des points de discontinuité d'une dérivée est donc un ensemble Fσ d'intérieur vide quelconque.
Théorème de Darboux[modifier | modifier le code]
Si est dérivable, sa fonction dérivée n'est donc pas nécessairement continue. Cependant, possède la propriété des valeurs intermédiaires. Ceci constitue le théorème de Darboux, qui peut se formuler de deux façons équivalentes :
- si dérivable est définie sur un intervalle réel , alors est un intervalle ;
- si alors, pour tout de , il existe tel que .
Dérivées de fonctions liées[modifier | modifier le code]
Beaucoup de problèmes font intervenir plusieurs variables qui sont liées entre elles et qui varient en fonction du temps.
La variation de l'une de ces variables donnera une variation correspondante des autres variables.
Le lien entre ces variations dépendra des relations qui existent entre les variables.
Un homme s'éloigne d'une tour de 60 m de hauteur à raison de 8 km/h soit environ 2,2 m/s.
À quelle vitesse s'éloigne-t-il du sommet de cette tour lorsqu'il est à 80 m du pied de la tour ?
On sait par relation de Pythagore que la distance entre le piéton et le sommet est alors de 100 m.
Avec et , distances du piéton au sommet de la tour et au pied de celle-ci sont des fonctions du temps liées par la relation de Pythagore :
- implique
En dérivant les deux membres de cette égalité, nous obtenons :
- implique :
la vitesse par rapport au sommet de la tour vaut le rapport entre la distance au sol entre le piéton et le pied de la tour et la distance entre le piéton et le sommet de la tour multiplié par la vitesse du piéton.
Lorsque le piéton est à 80 m du pied de la tour :
- ,
ce qui revient à dire que la vitesse par rapport au sommet de la tour vaut .
L'expression précédente permet en outre d'exprimer en fonction du temps la vitesse mesurée du sommet de la tour : si l'on note celle-ci et la vitesse constante de déplacement horizontal exprimées en m/s, on a les égalités
- .
Analyse d'une fonction dérivée[modifier | modifier le code]
En trouvant les valeurs de pour lesquelles la dérivée vaut 0 ou n'existe pas, on trouve les nombres critiques de la fonction. Les nombres critiques de permettent de trouver implicitement ses maxima et ses minima. En effectuant le test de la dérivée première, on construit un tableau de variation ; si le signe de la fonction dérivée passe du plus au moins devant un nombre critique, on a un maximum et si le signe de la fonction dérivée passe du moins au plus devant le nombre critique, on a un minimum.
De plus, lorsque le signe de la dérivée première est positif, la fonction est croissante ; s'il est négatif, elle est décroissante. On ne conclut rien, si au point critique la fonction dérivée ne change pas de signe. En dérivant la dérivée première, on a la dérivée seconde. En effectuant le test de la dérivée seconde, on trouve les nombres critiques de la dérivée première pour les placer dans le même tableau ; lorsqu'on observe un changement de signe de la dérivée seconde devant ce ou ces nombres critiques, on dit qu'on a un (ou des) point(s) d'inflexion. Les points d'inflexion marquent un changement de la concavité de la fonction. Un signe positif de la dérivée seconde signifie que la fonction est convexe et un signe négatif de la dérivée seconde signifie que la fonction est concave. Connaissant les changements de concavité et les extrema de la fonction, on peut alors tracer une esquisse de sa représentation graphique.
Dérivée et optimisation[modifier | modifier le code]
Méthode pour optimiser un rendement à l'aide du calcul différentiel :
- Mathématisation
- Définitions et dessin : on définit les variables inconnues et on les représente sur un schéma.
- Écrire la fonction objectif à deux variables et préciser si on recherche un maximum ou un minimum dans la situation donnée.
- Trouver la relation entre les deux variables.
- Écrire la fonction objectif à une variable et préciser le domaine de la fonction.
- Analyse
- Dériver la fonction pour obtenir la dérivée première.
- Trouver les nombres critiques de la fonction, où la dérivée première vaut zéro ou n'existe pas dans les intervalles du domaine.
- Effectuer le test de la dérivée première ou le test de la dérivée seconde pour déterminer le maximum ou le minimum recherché de la situation.
- On formule la réponse de façon concise par rapport à la question.
Dérivée algébrique[modifier | modifier le code]
Les algébristes donnent un sens un peu différent au terme dérivée. Ils l'appliquent à une structure appelée A-algèbre associative unitaire et commutative. Une application , de dans est appelée une dérivation si :
- l'application est A-linéaire ;
- et étant deux éléments de , la dérivée de est égale à la somme du produit de la dérivée de et de et du produit de avec la dérivée de :
(en particulier, la dérivée de l'élément neutre de pour la multiplication est nulle).
Un exemple de dérivation définie de cette manière est donné dans l'article polynôme formel.
Dérivée fractionnaire[modifier | modifier le code]
Une autre généralisation part de la notion de dérivée n-ème pour construire, à l'aide de la transformation de Laplace, une nouvelle fonction, la dérivée t-ème, où t est un réel quelconque, et qui coïncide avec la dérivée itérée si t est entier et si la fonction de départ est suffisamment régulière.
Dérivation en tant qu'application linéaire[modifier | modifier le code]
La dérivation est une application linéaire, de l'espace vectoriel des fonctions dérivables sur un intervalle ouvert non vide de et à valeurs réelles, vers celui des fonctions quelconques de dans [5]. Son noyau est constitué des fonctions constantes et plus généralement, tout réel est valeur propre, de sous-espace propre associé la droite de toutes les fonctions de la forme avec .
La dérivation en tant qu'endomorphisme de l'espace n'admet pas de racine carrée[6],[7], c'est-à-dire que si l'on note l'opérateur de dérivation, alors il n'existe pas[8] d'application linéaire telle que .
Notes et références[modifier | modifier le code]
- (en) Florian Cajori, A History of Mathematical Notations [détail des éditions], section 575, aperçu sur Google Livres.
- Cajori, section 567, aperçu sur Google Livres.
- (en) Michaël Baudin, « Scilab is not naive », sur scilab.org, p. 22-28.
- (en) Andrew M. Bruckner (en), Differentiation of Real Functions, Springer, (lire en ligne), p. 46-47.
- Cette application n'est pas surjective : son image (l'ensemble des fonctions admettant une primitive) ne contient pas, par exemple, de fonctions présentant une discontinuité de première espèce, en raison du théorème de Darboux (voir supra).
- Serge Francinou, Hervé Gianella et Serge Nicolas, Oraux X-ENS : Exercices de mathématiques Algèbre 1, t. 1, Paris, Cassini, , 372 p. (ISBN 978-2-84225-132-1), p. 311.
- Il est cependant possible, en un sens étendu, de définir une notion de dérivée fractionnaire ; pour cette définition, la dérivation d'ordre 1/2 est effectivement une racine carrée de la dérivation usuelle.
- En effet, la droite et le plan étant alors stables par , on aurait et , or les deux équations et sont incompatibles.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Toute fonction continue à dérivée nulle sauf sur un ensemble dénombrable est constante, d'après le lemme de Cousin ou l'inégalité des accroissements finis
- Toute fonction absolument continue à dérivée nulle presque partout aussi, à nouveau d'après le lemme de Cousin
- Notations delta en sciences
- Fonction à dérivée faible
- Sous-différentiel d'une fonction convexe
- Dérivée de Radon-Nikodym d'une mesure par rapport à une autre
- Calcul infinitésimal
- Dérivation

Lien externe[modifier | modifier le code]
(en) Eric W. Weisstein, « Derivative », sur MathWorld
Bibliographie[modifier | modifier le code]
Claude Wagschal, Dérivation, intégration. Avec exercices corrigés, Hermann, 2012












![{\displaystyle [x_{0},x_{0}+h]\subset {\mathcal {D}}_{f}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04a91415be77b2d808cc9504a8758d2ebaffd430)


















![{\displaystyle ]-\infty ,0[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83a3a204074bde51e56b7965e8c98a66888bbf88)
![{\displaystyle ]0,+\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e91ea5ab8b69e30f90c2bdf5db4b620815bde815)












































![{\displaystyle \left[x_{i-1},x_{i+1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c079bc3994e80a6e43e1a9e08a25976e857dfdb0)





































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle ]a,b[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b51ec208e9582e11a4f340a42d4f17fb4748fcb)










![{\displaystyle [f'(a),f'(b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eccc9f01e13e47681ea2495113019d527701e520)
























![{\displaystyle \ker D\cong \mathbb {C} _{0}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b0f99e7f978bb7470405f4a2b020df777b1d723)
![{\displaystyle \ker(D^{2})\cong \mathbb {C} _{1}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93add31e8ccc1d86c293ced296ccec01bc46bbba)




