État quantique
L'état d'un système physique décrit tous les aspects de ce système, dans le but de prévoir les résultats des expériences que l'on peut réaliser. Le fait que la mécanique quantique soit non déterministe entraîne une différence fondamentale par rapport à la description faite en mécanique classique : alors qu'en physique classique, l'état du système détermine de manière absolue les résultats de mesure des grandeurs physiques, une telle chose est impossible en physique quantique et la connaissance de l'état permet seulement de prévoir, de façon toutefois parfaitement reproductible, les probabilités respectives des différents résultats qui peuvent être obtenus à la suite de la réduction du paquet d'onde lors de la mesure d'un système quantique. Pour cette raison, on a coutume de dire qu'un système quantique peut être dans plusieurs états à la fois. Il faut en réalité comprendre que le système est dans un état quantique unique, mais que les mesures peuvent donner plusieurs résultats différents, chaque résultat étant associé à sa probabilité d'apparaître lors de la mesure.
L'état doit donc être vu comme représentant toute l'information disponible sur le système : une description de l'histoire du système permettant de calculer les probabilités de mesure. Dans le débat philosophique concernant l'interprétation de la mécanique quantique, certaines approches telles que l'interprétation de Copenhague considèrent d'ailleurs que l'état quantique n'est pas un élément de réalité au sens qu'Einstein donnait à ce terme, mais simplement un intermédiaire de calcul utile pour prévoir les mesures ; d'autres approches font appel à la notion de décohérence quantique pour décrire le processus mis en œuvre lors d'une mesure quantique.
L'une des conséquences de la nature aléatoire des mesures quantiques est que l'état ne peut être assimilé à un ensemble de propriétés physiques qui évoluent au cours du temps. En mécanique quantique, l'état et les grandeurs physiques sont deux concepts séparés et sont représentés par deux objets mathématiques différents. Dirac a montré qu'il était équivalent de faire porter l'évolution temporelle sur l'état quantique ou sur les grandeurs physiques, appelées observables en mécanique quantique.
La notion d'état en mécanique classique
[modifier | modifier le code]En mécanique classique, l'état d'un système est représenté par un ensemble de grandeurs physiques à partir duquel on peut déterminer toutes les propriétés du système concerné. Par exemple dans le cas d'un point matériel, l'état est complètement décrit par la donnée du vecteur position et de la quantité de mouvement . Autrement dit, l'état du système est repéré par un point dans l'espace des phases, qui est de dimension 6 pour un point matériel. Une fois l'état du système déterminé par la mesure, on peut d'une part calculer toutes les grandeurs mesurables sur le système comme l'énergie cinétique et potentielle, mais également calculer l'état du système à un instant ultérieur grâce à l'équation fondamentale de la dynamique.
L'espace des états dépend du système considéré : si l'on considère non plus un mais N points matériels, l'état du système sera repéré par un point dans un espace vectoriel de dimension 6N, car il faut garder la trace de la position et de l'impulsion de chacun des N points matériels ; dans le cas d'un milieu continu, comme un fluide ou un solide déformable, ou encore dans le cas du champ électromagnétique, l'état du système est décrit par des champs formant un espace vectoriel de dimension infinie : potentiel scalaire et potentiel vecteur, champ de déformation, de densité massique, de vecteurs vitesse, … Là encore, d'autres grandeurs physiques mesurables peuvent être dérivées (champ de pression, forces exercées sur un objet), et l'état du système à l'instant peut se déduire de l'état du système à l'instant à partir de lois dynamiques (Équations de Navier-Stokes, Équations de Maxwell). De manière générale, lorsque le système obéit à la mécanique lagrangienne, son état peut être décrit à l'aide des coordonnées généralisées.
Le déterminisme de l'évolution des états en mécanique classique est décrit de manière particulièrement claire par Laplace :
« Nous devons envisager l'état présent de l'univers comme l'effet de son état antérieur, et comme la cause de celui qui va suivre. Une intelligence qui, pour un instant donné, connaîtrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent, si d'ailleurs elle était assez vaste pour soumettre ces données à l'analyse, embrasserait dans la même formule les mouvements des plus grands corps de l'univers et ceux du plus léger atome : rien ne serait incertain pour elle, et l'avenir, comme le passé, serait présent à ses yeux. »
— Pierre-Simon de Laplace, Essai philosophique sur les probabilités (1814)
En mécanique statistique, l'état est décrit différemment : comme une distribution de probabilité sur l'espace des états. Il est toutefois compris que cette description n'est qu'une approximation liée à notre incapacité de mesurer parfaitement l'état d'un système contenant un grand nombre de degrés de liberté.
La notion d'état en mécanique quantique – état et mesure
[modifier | modifier le code]En mécanique quantique, il n'est pas possible de supposer que les grandeurs physiques telles que la position ou la vitesse aient une valeur définie que l'on puisse mesurer sans perturber le système. Au lieu de cela, les observations effectuées sur un système vont modifier son état, de sorte que les résultats des mesures ultérieures vont dépendre de l'ensemble des mesures effectuées précédemment. L'état du système doit donc être défini indépendamment des grandeurs physiques observables et plutôt être vu comme une description de ce qui a été fait sur le système ainsi que des résultats obtenus lors des mesures. Pauli qualifiait « d'idéalisation de l'observateur détaché » le point de vue selon lequel l'état se résume à une liste de grandeurs physiques préexistant à la mesure[1]. Mathématiquement, cette distinction se traduit par l'utilisation de deux objets différents pour représenter l'état et les observables du système.
De plus, on doit composer avec la nature irréductiblement aléatoire des résultats de mesure en mécanique quantique. Considérons par exemple l'équivalent quantique d'un point matériel, c’est-à-dire une particule sans spin. Les grandeurs physiques observables, ou plus simplement les observables sont en effet les mêmes dans les deux cas : la position, l'impulsion, l'énergie cinétique, l'énergie potentielle, l'énergie totale, ... Supposons que l'on soit capable de préparer notre particule dans un état i bien déterminé. On peut concevoir une expérience permettant de mesurer la position, par exemple en éclairant la particule, qui donnera comme résultat : 'la particule est en r1'. On pourrait alors en conclure que la position d'une particule préparée dans l'état i est r1. Cependant, si l'on réitère l'expérience en plaçant à nouveau la particule dans l'état i, on obtient une autre position r2 ≠ r1 " Sauf cas particulier", il en serait de même avec toute autre grandeur observable.
Au cours du temps, les physiciens ont acquis la conviction que ce fait expérimental n'était pas dû à une incertitude expérimentale lors de la mesure, ou encore à une préparation aléatoire d'une fois sur l'autre (dans un état i'i), mais plutôt que l'état ne détermine pas les résultats de mesure de manière certaine. Ceci est particulièrement illustré lors d'expériences mettant en évidence la complémentarité quantique, où malgré des mesures permettant de préparer un état précis, les résultats des mesures ultérieures restent aléatoires.
En traitant statistiquement les valeurs r1, r2, ... obtenues lors de mesures répétées de la position, comme dans la première figure ci-dessous, il apparaît cependant que certaines sont obtenues plus fréquemment que d'autres. Ainsi, si la valeur obtenue à l'issue de chaque mesure individuelle n'est pas connue, l'état détermine la distribution de probabilité associée à chacune des observables du système, et sa connaissance nous permet de faire des prévisions probabilistes sur les résultats de mesure. Il est alors possible de définir des grandeurs statistiques telles que la valeur moyenne de la position ou encore l'écart type de la position (notées et respectivement dans le cas de la position, et et dans le cas d'une observable O quelconque, étant également appelée incertitude sur la grandeur O lorsque la particule est dans l'état i).
Un cas particulier intéressant correspond à des états pour lesquels l'incertitude ΔO est nulle pour une des observables O. On retrouve alors la prévision de la mécanique classique : dans un de ces états, la mesure de O donnera toujours le même résultat. Pour distinguer ces états là des autres états, ils sont appelés états propres de l'observable O. Les états propres de l'énergie totale présentent l'intérêt de ne pas évoluer au cours du temps : si une particule est dans un état d'énergie donnée, elle restera dans cet état par la suite.
Enfin, un dernier cas particulier permet de préciser ce qui est sous-entendu lorsque l'on dit qu'une particule est dans deux états simultanément. On peut imaginer un état où la distribution de probabilité de la grandeur O est piquée sur deux valeurs. En fait, la particule n'est en réalité que dans un seul état, mais cet état quantique donnera deux résultats possibles lors d'une mesure de O.
-
Histogramme : statistique des résultats de N=5000 mesures de la position d'un ensemble de N particules toutes préparées dans le même état. Courbe : densité de probabilité de présence mise à la même échelle.
-
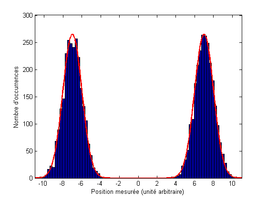
Mesure de la position d'un ensemble de particules dans une superposition d'états.
Représentation mathématique d'un état
[modifier | modifier le code]État pur
[modifier | modifier le code]En mécanique quantique, on représente l'état d'un système par un vecteur dans un espace vectoriel hilbertien, c'est-à-dire dans lequel est défini un produit scalaire hermitien entre deux vecteurs φ et ψ. En raison de l'importance de ces produits scalaires, on utilise la notation bra-ket introduite par Dirac[2] pour représenter les états quantiques de manière concise et simple. Le vecteur ψ est ainsi noté et appelé ket, tandis que son vecteur dual est appelé bra et noté .
L'espace des états dépend du système considéré. Par exemple, dans le cas le plus simple où le système n'a pas de spin ou de structure interne, les états quantiques sont des fonctions telles que l'intégrale converge. Dans ce cas, ψ est appelée la fonction d'onde du système.
D'autre part, lorsque l'on associe deux systèmes pour en faire un seul, l'espace des états de ce système composé est le produit tensoriel des espaces des états associés aux deux sous-systèmes. (Dans le cas de deux particules identiques, il y a une restriction additionnelle, liée aux spin.)
On retrouve le déterminisme de la mécanique classique dans l'évolution de l'état quantique. C'est-à-dire que l'on peut calculer de manière déterministe comment l'état d'un système va évoluer au cours du temps (grâce à l'équation de Schrödinger), sauf lorsqu'il y a une mesure de l'état de notre système, auquel cas l'évolution n'est plus déterministe, mais probabiliste.
Il s'agit là d'une différence majeure avec la mécanique classique, qui découle du postulat de réduction du paquet d'onde et qui permet de donner une interprétation probabiliste aux états quantiques.
Représentations de Schrödinger et de Heisenberg
[modifier | modifier le code]Ces deux représentations sont deux manières équivalentes de décrire l'évolution temporelle du système quantique.
Selon Heisenberg, le vecteur d'état est constant, donc l'observable qui désigne les diverses variables d'un système quantique évolue dans le temps.
Mais Schrödinger par la suite, démontra que l'observable qui désigne les diverses variables d'un système quantique peut dépendre du temps. Sauf que ce facteur n'a pas de rapport direct avec l'évolution temporelle dictée par l'hamiltonien. On en conclut donc selon Schrödinger que les diverses variables d'un système quantique restent constantes au cours du temps.
États mixtes
[modifier | modifier le code]L'état quantique d'un système peut être représenté par la matrice densité. Il s'ensuit qu'un état mixte est un mélange statistique d'états purs. Tout état mixte, peut se mettre sous la forme suivante : , où les sont les probabilités du mélange statistique, et les sont les différents états purs du système.
Fonction de Wigner
[modifier | modifier le code]Interprétation probabiliste des états quantiques
[modifier | modifier le code]Dans les années 1920, Max Born a développé l'interprétation statistique des états quantiques pour laquelle il a reçu le prix Nobel en 1954[3]. Pour comprendre comment fonctionne cette interprétation, supposons qu'un système quantique se trouve dans un état et que l'on veuille mesurer une observable du système (énergie, position, spin, ...). Les vecteurs propres de sont notés et les valeurs propres correspondantes , que l'on supposera non dégénérées pour simplifier. Comme le postule le principe de réduction du paquet d'onde, la mesure de A ne peut donner comme résultat que l'un des , et la probabilité d'obtenir le résultat est . Supposons que la mesure donne pour résultat , le système est passé lors de la mesure et de façon instantanée de l'état à l'état .
On voit dès lors l'interprétation que l'on peut faire des produits scalaires , où est un état quelconque : en effet, en supposant l'existence d'une observable dont serait un des états propres, on peut dire que la probabilité de trouver le système dans l'état (sous-entendu : si on faisait la mesure) est . Pour cette raison, le produit scalaire est appelé amplitude de probabilité.
Le fait que la mesure d'une des propriétés du système change l'état de ce système fait que l'on ne peut pas mesurer ou cloner l'état quantique inconnu d'un système. En effet, on pourrait penser qu'en prenant deux systèmes faits des mêmes atomes et en mesurant l'état dans lequel est le système 1, on peut ensuite placer le système 2 dans le même état que le système 1 et ainsi en avoir une copie conforme, mais il faudrait pour cela effectuer plusieurs mesures sur le système 1, dont l'état sera irrémédiablement changé dès la première mesure. Le théorème de non clonage est la base des techniques de cryptographie quantique. La téléportation quantique, quant à elle, cherche à transporter de façon non destructive l'état du système 1 sur le système 2.
Détermination expérimentale de l'état d'un système
[modifier | modifier le code]S'il n'est pas possible de mesurer l'état d'un système unique, en répétant la même expérience un grand nombre de fois on peut toutefois déterminer la matrice densité d'un système. Il est pour cela nécessaire de faire tourner la base de mesure entre la base des états propres d'une grandeur et celle d'une grandeur qui lui est incompatible.
Superposition d'états, intrication et paradoxe de la mesure
[modifier | modifier le code]Si et sont deux états possibles du système, i.e. appartiennent à l'espace des états, la définition d'un espace vectoriel fait que toute combinaison linéaire de ces états sera un état possible du système. Pour illustrer l'étrangeté de ces superpositions d'états, Erwin Schrödinger a avancé le paradoxe du chat de Schrödinger : que penser d'un chat que l'on aurait mis dans la superposition d'états
Est-ce le fait qu'il y ait un observateur présent pour tenter de faire une mesure qui réduit le paquet d'onde instantanément à un et un seul des résultats possibles de la mesure ? Quelle est la particularité qui fait qu'un système quantique n'obéisse plus à l'équation déterministe de Schrödinger lors de l'interaction avec un appareil de mesure (ou plus généralement avec un objet macroscopique) ?
Bref, le principe de réduction du paquet d'onde dérange et contribue beaucoup à la réputation de la mécanique quantique d'être contre-intuitive. Après avoir suivi l'école de Copenhague pendant des dizaines d'années, la majorité des physiciens pensent aujourd'hui que l'intrication et la décohérence jouent un grand rôle dans l'explication du phénomène de réduction du paquet d'onde. Expérimentalement, il devient possible aujourd'hui de réaliser les expériences de pensée du début du XXe siècle et des groupes de recherche tentent de réaliser de petits « chats de Schrödinger », c'est-à-dire des objets mésoscopiques placés dans une superposition d'états pour étudier leur évolution. Pour décrire l'état quantique d'un objet intriqué, l'approche présentée ici à partir de la notation bra-ket n'est pas suffisante, et il convient d'utiliser le formalisme de la matrice densité.
Notes et références
[modifier | modifier le code]- Albert Einstein, Max Born et Hedwig Born (trad. de l'allemand), Correspondance 1916-1955 [« The Born-Einstein letters »], Paris, Seuil, coll. « Science Ouverte », , 255 p., broché [détail de l’édition] (ISBN 2-02-002813-1)
- Paul Dirac, Les Principes de la mécanique quantique [« The Principles of Quantum Mechanics »] (1re éd. 1930) [détail de l’édition]
- [PDF](en)Max Born, « The statistical interpretation of quantum mechanics (conférence Nobel) »,