Utilisateur:Alexandre alexandre/Brouillon

Si le diamètre du cercle est 1, sa circonférence est π.

En mathématique la lettre grecque $\pi$ (lire : "pi") désigne le rapport constant entre la circonférence d’un cercle et son diamètre dans le plan euclidien ; ce nombre réel est aussi la valeur du rapport entre l'aire d'un disque et le carré de son rayon. Il s'avère que cette définition géométrique, historiquement la première et la plus intuitive, a une (des) alternative plus rigoureuse faisant essentiellement usage des outils analytiques. Ainsi défini, on peut alors d'avantage cerner la nature de ce nombre réel :

• il est irrationnel, c.-à-d. qu'il ne peut se mettre sous la forme d'une fraction de deux entiers, et en particulier les valeurs 3,14 ; 3,1416 ; 22/7 ; 355/113 n'en sont que des approxiamtions,
• il est transcendant, ie qu'il ne vérifie aucune équation polynomiale à coefficients entiers, et en particulier celà prouve l'imossibilité de la quadrature du cercle.

La simplicité de sa définition et son omniprésence en mathématiques fascinent aussi bien le grand public, qui a introduit pi dans des ouvres non-scientifiques, et les mathématiciens qui continuent de s'intéresser à de nombreuses questions concernants pi et/ou ses décimales...

Aspects mathématiques

Approches géométriques

Il y a deux choses à justifier dans la définition géométrique proposée en introduction :

• le fait que le rapport circonférence/diamètre ne dépend pas du choix du cercle,
• le fait que ce rapport est aussi celui de l'aire du disque sur celle du carré ayant pour coté le rayon.

Pour le premier point on commence par se donner deux cercles. En translatant l'un d'eux on ne modifie pas son rapport circonférence/diamètre : on peut donc les supposer concentriques. Maintentant pour le superposer à l'autre, il suffit de l'agrandir ou de le rétrécir, ce qui multiplie la diamètre et la circonférence par un même coefficient et ne change donc toujours pas le rapport circonférence/diamètre. Celui-ci est donc le même pour les deux cercles, comme ceux-ci ont été choisi arbitrairement on peut définir $\pi :={\frac {C}{d}}$, indépendamment du choix du cercle.

Pour le second point, on se donne un cercle de rayon R. On construit à l'intérieur un polygone régulier à 2n cotés qu'on découpe en 2n triangles. En réarrangeant ces triangles comme sur le dessins on peut calculer l'aire du polygone (qui est "à peu près" celle du disque), puisqu'elle est égale à celle du parrallèlogramme ainsi formé. Or celui-ci à une base dont la longueur est "à peu près" la moitié de la circonférence, soit $\pi R$ ; et une hauteur "à peu près égale" au rayon. Bref son aire vaut "à peu près" $\pi R^{2}$. On peut formaliser le "à peu près" en augmentant indéfiniment le nombre de cotés du-dit polygone.

On obtient bien $\pi ={\frac {C}{2R}}={\frac {A}{R^{2}}}$.

Les premiers géomètres explorèrent un peu mieux et un peu plus rigoureusement cette approche géométrique de $\pi$ (cf. ). Néanmoins, pour dire des choses plus profondes sur $\pi$, on ne peut se passer d'une définition plus rigoureuse : c'est le but de la prochaine section.

Définition analytique

Une façon courante (sources) de définir $\pi$ de manière plus rigoureuse consiste à le voir comme la demi-période de l'exponentielle complexe, ou de manière équivalente, suivant que l'on veut faire l'économie des nombres complexes ou non, comme premier zéro >0 de la fonction sinus. On propose ci-après ces deux points de vue :

• le revetement $\mathbb {R} \to \mathbb {U}$,
• l'utilisation du couple cosinus,sinus.

Ces deux procédés relèvent de l'analyse à travers la complétude, mais quelques auteurs (sources) introduisent $\pi$ ou les fonctions trigonométriques par d'autre biais : l'intégration permet d'obtenir les fonctions circulaires réciproques, ou bien encore la valeur du résidu de $z\mapsto {\frac {1}{z}}$...

Exponentielle complexe

La complétude de $\mathbb {C}$ montre que l'application $\exp :\mathbb {C} \to \mathbb {C} ,\,z\mapsto \sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}$ prolonge l'exponentielle réelle à $\mathbb {C}$ tout entier et vérifie les propriétés suivantes :

• $\forall z,w\in \mathbb {C} ,\,\exp(z+w)=\exp(z)\exp(w)$,
• $\forall z\in \mathbb {C} ,\,{\overline {\exp(z)}}=\exp({\overline {z}})$.
• $\exp$ est une série entière partout convergente donc a fortiori continue et dérivable.

Le premier point motive la notation en puissance : $e^{z}:=\exp(z)$ déjà adoptée pour les réels. On tire du second point que pour tout réel $\theta$, $|e^{i\theta }|^{2}=e^{i\theta }{\overline {e^{i\theta }}}=e^{i\theta }e^{-i\theta }=e^{0}=1$. On introduit alors l'application $\phi :\mathbb {R} \to \mathbb {U} ,\theta \mapsto e^{i\theta }$ qui est un morphisme de groupes topologiques. Le but est alors de montrer qu'elle induit un isomorphisme de $\mathbb {R} /\ker \phi$ sur $\mathbb {U}$ et d'en déduire qu'il existe un unique réel positif, noté $\pi$, tel que $\ker \phi =2\pi$.

Voici quelques arguments topologiques pour trancher, on propose juste après une approche plus trigonométrique. Comme $\phi$ est non triviale (on peut voir que la partie imaginaire de $e^{1}$ est strictement positive), son image est un sous-groupe non-trivial connexe de $\mathbb {U}$ ce qui permet d'obtenir la surjectivité. Son noyau doit alors être fermé et comme $\mathbb {U}$ est compact, il est non trivial (et pas non-plus égal à $\mathbb {R}$), du coup il est de la forme $x\mathbb {Z}$ pour un unique réel $x>0$. On pose $\pi :={\frac {x}{2}}$.

Trigonométrie

On propose ici une définition à travers les fonctions sinus et cosinus qu'il faut donc définir proprement. Pour se faire on peut prendre les parties imaginaires et réelles de la fonction $\phi$ précédente, ou bien parachuter les séries entières $\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{k}$ et $\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{k}$. Dans les deux cas, on montre qu'il s'agit de fonctions dérivables sur $\mathbb {R}$ vérifiant : $\cos '=-\sin$ et $\sin '=\cos$.

On montre alors, par l'absurde, que cosinus s'annule. Sinon, comme elle est continue et positive en $0$ elle serait toujours strictement positive par le TVI, et par suite $\sin$ serait strictement croisssante : donnsons nous a>0 tel que $\sin a>0$. Alors on a pour tout x>a :

$\cos x-\cos a=\int _{a}^{x}-\sin tdt\leq \int _{a}^{x}-\sin adt=-(x-a)\sin a$

qui tend vers $-\infty$ quand $x\to \infty$ et donc $\cos x$ aussi, ce qui est la contradiction voulue. Bref $E:=\{\theta >0/\cos \theta =0\}$ est non vide. On pose alors ${\frac {\pi }{2}}:=\inf E$. Par continuité de $\cos$ on a $\cos {\frac {\pi }{2}}=0$ et ${\frac {\pi }{2}}$ est le plus petit réel strictement positif à vérifier cette relation. A partir de là, il ne serait pas difficile d'obtenir les propriété usuelles de ces deux fonctions, ce qui permet entre-autre, par le biais du calcul intégral de vérifier que cette définition redonne bien la "définition géométrique".

Vérifications

Il nous faut maintenant vérifier que défini ainsi, $\pi$ n'en reste pas moins le rapport périmètre/diamètre ou de façon équivalente l'aire d'un cercle de rayon 1. Pour ce faire on peut calculer l'aire d'un quart de cerle de rayon 1, ie l'aire sous la courbe $y={\sqrt {1-x^{2}}},\,0\leq x\leq 1$. Il vient, en posant $x=\cos \theta$ :

$\int _{0}^{1}{\sqrt {1-x^{2}}}dx=\int _{0}^{\frac {\pi }{2}}\sin ^{2}\theta d\theta =\int _{0}^{\frac {\pi }{2}}{\frac {1-\cos 2\theta }{2}}d\theta ={\frac {\pi }{4}}-\left[{\frac {\sin 2\theta }{4}}\right]_{0}^{\frac {\pi }{2}}={\frac {\pi }{4}}$.

Si l'équivalence géométrique ne nous convient pas, le calcul intégral permet également de montrer que la longueur, disons d'un demi-cercle de rayon 1, vaut bien $\pi$.

Quelques propriétés mathématiques de $\pi$

Nature de $\pi$

Le fait que $\pi$ soit le premier zéro de sinus conduit à une preuve élémentaire de son irrationalité, ie qu'on ne peut le mettre sous une forme de fraction a/b avec a et b entiers. Pour le voir on procède par l'absurde et on considère par exemple (une autre preuve sera fournie dans la partie Histoire) intégrales suivantes $I_{n}:={\frac {1}{n!}}\int _{0}^{\pi }x^{n}(a-bx)^{n}\sin xdx$. Elles sont toutes strictement positives justement parceque l'intégrande est positif et non identiquement nul. Par contre on peut majorer x(a-bx) sur $[0,\pi ]$ disons par M et donc $I_{n}\leq \pi {\frac {M^{n}}{n!}}$ tend vers 0 avec n. Enfin, on montre en intégrant 2n+1 fois par parties, que $I_{n}$ est un entier ce qui amène la contradiction.

Ainsi $\pi$ n'est pas rationnel, a fortiori non décimal et ne présente même pas un developpement décimal périodique. En connaître toujours plus de décimales deviendra un défi pour les mathématiciens et les informaticiens (cf l'endroit qui en reparlera). Il se pose alors les questions naturelles sur ces décimales : font-elles intervenir tous les nombres de manière égale ? contiennent-elles n'importe quelle séquence de chiffres ?

Plus difficilement, on peut montrer que $\pi$ est transcendant, ie n'annule aucun polynome non nul à coefficient entier. [plus de détails ici ou dans la partie historique ?] Ce résultat et celui de Wantzel expliquent pourquoi les grecs n'avaient pu quarrer un cercle, ie construire, à la règle et au compas un carré de même aire qu'un disque donnée : c'est en effet impossible !

Quelques formules remarquables

[j'en suis pas fan du tout et ca me parait tres arbitraire, mais j'y berrais quand même] stirling, intégrale gaussienne, formule des résidus

Bien sûr on a les formules de géométrie classique concernant les cercles ($C=\pi d,\,A=\pi R^{2}$), les sphères ($S=4\pi R^{2},\,V={\frac {4\pi }{3}}R^{3}$)...

Par définition, on a vu que $e^{i\pi }+1=0$, qui pour certains (sources) est l'une des plus jolies formules mathématiques puisqu'elle utilise les symboles fondamentaux que sont : 0, 1, e, i, $\pi$, =, +.

Ceci-dit $\pi$ apparait dans d'autres domaines des mathématiques :

• en analyse encore, au travers de la formule de Stirling $n!\sim {\sqrt {2n\pi }}\left({\frac {n}{e}}\right)^{n}$,
• en analyse complexe, dans le théorème des résidus $\mathrm {Res} _{a}f={\frac {1}{2i\pi }}\int _{C}f$,
• en probabilité via le calcul de l'intégrale gausienne $\int _{\mathbb {R} }e^{-x^{2}}dx={\sqrt {\pi }}$,
• encore en "probabilité/arithmétique" puisque la probabilité que deux nombres pris aléatoirement entre 1 et n soient premiers entre-eux tend vers ${\frac {6}{\pi ^{2}}}={\frac {1}{\zeta (2)}}$ quand n tend vers l'infini...

A propos des décimales de $\pi$

Quelques questions ouvertes

On ne sait pas si e et pi sont algébriquement indépendants... (après j'en sais rien, peut-être des question sur la répartition des décimales ?)

Il y en a quelques unes sur ce lien, par exemple dzeta de 3 divisé par Pi au cube est-il un rationnel (cf ce qui passe avec la fonction zêta de Riemann calculée sur les entiers pairs.

Histoire

L'histoire ancienne de π, qu'on peut retracer grâce aux écrits disponibles, suit approximativement l'avancée des mathématiques dans leur ensemble. Certains auteurs divisent l'histoire de π en trois parties : la période antique durant laquelle π a été étudié géométriquement, l'ère classique, aux alentours du XVII^e siècle, où les outils du calcul intégral ont permis des avancées dans notre connaissance du nombre π, et la période des ordinateurs numériques.

Antiquité

Il semble que, très tôt, les mathématiciens aient été convaincus qu’il existait un rapport constant entre le périmètre du cercle et son diamètre, ainsi qu’entre l’aire du disque et le carré du diamètre. Des tablettes babyloniennes datant de 2000 ans avant J.-C. et découvertes en 1936 présentent des calculs d’aire conduisant à une valeur de π de 3+1/8.

Approximation de π par Ahmès

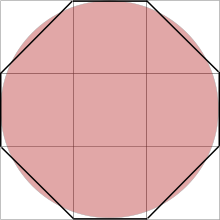
Découvert en 1855, le papyrus de Rhind contient le texte, recopié vers l’an 1650 avant notre ère par le scribe égyptien Ahmès, d’un manuel de problèmes pédagogique plus ancien encore. On y trouve une méthode pour évaluer l’aire d’un disque en prenant le carré dont le côté est égal au diamètre du disque diminué d’un neuvième. Cette méthode conduit à une évaluation de π de ²⁵⁶⁄₈₁. Dans l’illustration ci-contre, le disque a pour diamètre 9. L’aire du disque est légèrement supérieure à l’aire de l’octogone irrégulier obtenu en rognant les coins du carré de côté 9. Cet octogone a pour aire 63, l’aire du disque est alors évaluée à 64 soit l’aire d'un carré de côté 8. Le rapport entre l'aire du disque et le carré du rayon est alors évalué par 64/(9/2)² , c'est-à-dire 256/81.

Le texte indien Shatapatha Brahmana donne à π une valeur de 339/108 ≈ 3,139^{[réf. nécessaire]}.

C’est chez Archimède (-287, -212), dans son traité De la mesure du cercle que l’on peut lire une démonstration liant l’aire du disque et l’aire du triangle ayant pour base le périmètre du cercle et pour hauteur le rayon, démontrant ainsi qu'une même constante apparait dans le rapport entre aire du disque et carré du rayon et entre périmètre et diamètre.

Cette démonstration s’appuie sur la méthode d'exhaustion et un raisonnement par l'absurde. En partant d’un carré inscrit dans le cercle et d’un carré circonscrit au cercle et en multipliant indéfiniment par 2 le nombre de côtés, il prouve que l’aire du disque ne peut être inférieure ni supérieure à celle du triangle correspondant.

• 
  Cercle et ses carrés inscrit et circonscrit
• 
  Cercle et ses octogones inscrit et circonscrit
• 
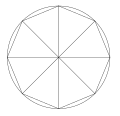
  Découpage du cercle en 8 portions de camembert

Sa démonstration exploite l’idée du découpage en quartiers : le cercle est découpé en plusieurs quartiers qui, mis bout à bout, dessinent des triangles curvilignes de même hauteur. En multipliant le nombre de quartiers, la base des triangles curvilignes est presque droite et la hauteur est proche du rayon, la somme des bases correspond alors au périmètre du cercle et l’aire est alors de ¹⁄₂ de la base multipliée par la hauteur, c’est-à-dire ¹⁄₂ du périmètre multiplié par le rayon.

Déroulement des 8 portions

La seconde démonstration consiste à encadrer le périmètre du cercle par le périmètre de polygones réguliers inscrit et circonscrit au cercle et possédant 96 côtés. Pour calculer les périmètres de ces polygones, il part d’hexagones inscrits et circonscrits et met en évidence les formules donnant le périmètre d’un polygone dont le nombre de côtés a doublé. Il démontre ainsi que 3 + 10/71 < π < 3 + 1/7. La moyenne de ces deux valeurs est d'environ 3,14185. Archimède s’arrête à 96 côtés car les calculs qu’il est amené à effectuer, avec valeurs approchées, sont déjà longs pour l’époque. Mais il met en place ainsi une méthode qui sera reprise par ses successeurs et qui peut en théorie être poursuivie indéfiniment. Ptolémée, scientifique grec ayant vécu trois siècles après Archimède, donne une valeur de 3,1416, qu'il a probablement obtenu grâce à Apollonius de Perga^{[source insuffisante]}.

Formules d'Archimède

Propriété de la bissectrice

Archimède utilise une propriété liant le pied d’une bissectrice aux côtés adjacents : Dans la figure ci-contre SS′ est la bissectrice de l’angle de sommet S

${\frac {x}{a}}={\frac {y}{b}}={\frac {x+y}{a+b}}$

Polygone circonscrit

Pour le polygone circonscrit. Dans la figure ci-dessous (gauche), $c_{1}$ et $c_{2}$ sont les demi-côtés de deux polygones circonscrits consécutifs. Archimède montre, en utilisant la propriété précédente, que

${\frac {c_{1}}{c_{2}}}=1+{\frac {d_{1}}{r}}$

${\frac {d_{1}}{r}}={\sqrt {1+\left({\dfrac {c_{1}}{r}}\right)^{2}}}$

et réitère 4 fois l’opération à partir de l’hexagone.

Polygone inscrit

Pour le polygone inscrit. Dans la figure ci-contre, $c_{1}$ et $c_{2}$ sont les côtés de deux polygones inscrits consécutifs. Archimède montre, en utilisant les triangles semblables et la propriété de la bissectrice que

${\frac {d_{2}}{c_{2}}}={\frac {2r}{y}}={\dfrac {2r}{c_{1}}}+{\frac {d_{1}}{c_{1}}}$

${\frac {2r}{c_{2}}}={\sqrt {1+\left({\dfrac {d_{2}}{c_{2}}}\right)^{2}}}$

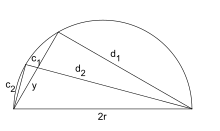
De nos jours, les formules trigonométriques permettent de simplifier l’algorithme d’Archimède. Les périmètres $p_{i}$ et $P_{i}$ des polygones inscrits et circonscrits vérifient les relations de récurrence suivantes

${\frac {1}{P_{n+1}}}={\frac {1}{2}}\left({\frac {1}{p_{n}}}+{\frac {1}{P_{n}}}\right)$

$p_{n+1}={\sqrt {p_{n}P_{n+1}}}$

En effet, pour un cercle de rayon 1, si on note $a_{n}$ la moitié de l’angle au centre des polygones à l’étape n, on sait que

$p_{n}=2n\sin(a_{n})\,$

$P_{n}=2n\tan(a_{n})\,$

$p_{n+1}=4n\sin(a_{n}/2)\,$

$P_{n+1}=4n\tan(a_{n}/2)\,$

et

${\frac {1}{2}}\left({\frac {1}{p_{n}}}+{\frac {1}{P_{n}}}\right)={\frac {1}{4n}}{\frac {1+\cos(a_{n})}{\sin(a_{n})}}={\frac {1}{4n}}{\frac {2\cos ^{2}(a_{n})}{2\sin(a_{n}/2)\cos(a_{n}/2)}}={\frac {1}{4n}}{\frac {1}{\tan(a_{n}/2)}}={\frac {1}{P_{n+1}}}$

${\sqrt {p_{n}P_{n+1}}}={\sqrt {8n^{2}\sin(a_{n}){\frac {\sin(a_{n}/2)}{cos(a_{n}/2}}}}={\sqrt {16n^{2}\sin ^{2}(a_{n}/2)}}=4n\sin(a_{n}/2)=p_{n+1}$

 

Encadrement de Liu Hui

Si les calculs pratiques peuvent se satisfaire de la valeur 3,14 comme bonne approximation de π, la curiosité des mathématiciens les pousse à déterminer ce nombre avec plus de précision. Au III^e siècle, en Chine, Liu Hui, commentateur des Neuf chapitres, propose comme rapport entre le périmètre et le diamètre la valeur pratique de 3 mais développe des calculs proches de ceux d’Archimède mais plus performants et fournit une approximation de π de 3,1416. Le mathématicien chinois Zu Chongzhi donne une approximation rationnelle encore plus précise de π : π ≈ 355/113 (dont les développement décimaux sont identiques jusqu'à la 6ème décimale, π ≈ 3,1415926 et 355/113 ≈ 3,1415929) et montre que 3,1415926 < π < 3.1415927, en utilisant l'algorithme de Liu Hui appliqué à un polygône de 12 288 côtés. Cette valeur va demeurer la meilleure approximation de π au cours des 900 prochaines années..

Ere classique

De la nature de $\pi$

π est un nombre irrationnel, ce qui signifie qu'on ne peut pas écrire π=p/q où p et q seraient des nombres entiers. Al-Khawarizmi mentionne dès le IX^e siècle sa croyance selon laquelle π est irrationnel. Moïse Maïmonide fait également état de cette idée durant le XII^e siècle. Il faudra cependant attendre le XVII^e siècle pour que Johann Heinrich Lambert prouve ce résultat.

C'est en 1761 que dans son Mémoires sur quelques propriétés remarquables des quantités transcendantes, circulaires et logarithmiques, ce dernier étudie le développement en fraction continue de tan(x) et montre que, lorsque x est rationnel, le développement en fraction continue de tan(m/n) est

$\tan \left({\frac {m}{n}}\right)={\frac {m\mid }{\mid n}}-{\frac {m^{2}\mid }{\mid 3n}}-{\frac {m^{2}\mid }{\mid 5n}}-{\frac {m^{2}\mid }{\mid 7n}}+\cdots$

Par conséquent, lorsque x est rationnel, le développement en fraction continue de tan(x) est illimité. Or, on sait qu’un développement illimité conduit à un nombre irrationnel. Bref, quand x est rationnel, tan(x) est irrationnel. Or, tan(π/4) vaut 1, c’est un rationnel. Par contraposée, on peut affirmer que π/4 n’est pas rationnel.

Au cours du XX^e siècle, d'autres démonstrations furent trouvées [L'une d'entre-elles correspond-elle à celle faites plus haut ?], celles-ci ne demandant pas de connaissances plus avancées que celle du calcul intégral. L'une d'entre elles, due à Ivan Niven, est très largement connue. Une preuve similaire avait été trouvée quelques temps auparavant par Mary Cartwright.

π est aussi un nombre transcendant, c'est-à-dire qu'il n'existe pas de polynôme à coefficients rationnels dont π soit une racine.

C'est seulement au XIX^e siècle que la transcendance de $\pi$ dera démontrée. En 1873, Charles Hermite prouve que la base du logarithme népérien, le nombre e, est transcendant. En 1882, Ferdinand von Lindemann généralise son raisonnement en un théorème (Théorème d'Hermite-Lindemann) qui stipule que, si x est algébrique, alors e^x est transcendant. Or e^iπ = -1 donc e^iπ n’est pas transcendant. Par contraposée, iπ n’est pas algébrique et π est transcendant.

Une conséquence importante de la transcendance de π est que celui-ci n'est pas constructible. En effet, le théorème de Wantzel énonce en particulier que tout nombre constructible est algébrique. En raison du fait que les coordonnées de tous les points pouvant se construire à la règle et au compas sont des nombres constructibles, la quadrature du cercle est impossible ; autrement dit, il est impossible de construire, uniquement à la règle et au compas, un carré dont la superficie serait égale à celle d'un cercle donné. Ce résultat a une importance historique, étant donné que le problème de la quadrature du cercle est l'un des problèmes de géométrie élémentaire qui nous vient de l'Antiquité les plus faciles à comprendre.

De meilleures approximations

Jusqu'au II^e millénaire, la précision des approximations de π n'excédait pas les 10 décimales. Les progrès en matière de calcul intégral et de séries vont permettre d'acquérir de plus amples connaissances sur π. Les séries permettent par ailleurs d'approcher π avec le plus de précision que l'on désire, en considérant simplement assez de termes dans la série. Environ en 1400, Madhava de Sangamagrama trouve une telle série, la première :

${\pi }=4\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{2k+1}}={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+\cdots \!$

Cette série, qui est en fait un cas particulier de

$\arctan(x)=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+...=\sum _{k=0}^{\infty }{\frac {(-1)^{k}x^{2k+1}}{2k+1}}$,

est maintenant connue sous le nom de série de Madhava-Leibniz ou série de Gregory-Leibniz depuis que la formule a été redécouverte par James Gregory et Gottfried Wilhelm Leibniz au XVII^e siècle. Malheureusement, la vitesse de convergence de cette série est trop lente pour pouvoir calculer, en pratique, plusieurs décimales : environ 4 000 termes sont nécessaires pour arriver à la précision qu'avait atteint Archimède. Cependant, en transformant la série de la façon suivante

$\pi ={\sqrt {12}}\sum _{k=0}^{\infty }{\frac {(-3)^{-k}}{2k+1}}={\sqrt {12}}\sum _{k=0}^{\infty }{\frac {(-{\frac {1}{3}})^{k}}{2k+1}}={\sqrt {12}}\left(1-{1 \over 3\cdot 3}+{1 \over 5\cdot 3^{2}}-{1 \over 7\cdot 3^{3}}+\cdots \right),$

Madhava a été capable de donner une valeur approchée de π de 3,14159265359, qui a 11 décimales correctes. Le record a été battu en 1424 par le mathématicien perse Al-Kachi, qui a réussi à donner 16 décimales.

La première contribution importante venant d'Europe depuis Archimède a été faite par l'allemand Ludolph van Ceulen (1540–1610), qui a utilisé une méthode géométrique afin de donner une estimation de π correcte à 35 décimales près. Il a été si fier de son calcul, qui lui a demandé une grande partie de sa vie, qu'il a fait graver les décimales sur sa pierre tombale.

Dans la même période, les méthodes de calcul intégral et de détermination de séries et produits infinis pour des quantités géométriques ont commencé à émerger en Europe. La première formule de ce type est la formule de Viète :

${\frac {2}{\pi }}={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdot \cdots \!$

trouvée par François Viète en 1593. Un autre résultat célèbre est le produit de Wallis :

${\frac {\pi }{2}}=\prod _{k=1}^{\infty }{\frac {(2k)^{2}}{(2k)^{2}-1}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots \ ={\frac {4}{3}}\cdot {\frac {16}{15}}\cdot {\frac {36}{35}}\cdot {\frac {64}{63}}\cdots \!$

que l'on doit à John Wallis, qui l'a mis en évidence en 1655. Isaac Newton lui-même a utilisé le développement en série de π/6=arcsin 1/2 pour calculer 15 décimales de π ; bien plus tard, il a déclaré : « J'ai honte de vous dire combien de décimales j'ai trouvé grâce à ces calculs, n'ayant aucune autre occupation à l'époque. ».

En 1706, John Machin a été le premier à trouver 100 décimales de π, en utilisant la formule

${\frac {\pi }{4}}=4\,\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}\!$

avec

$\arctan \,x=\sum _{k=0}^{\infty }{\frac {(-1)^{k}x^{2k+1}}{2k+1}}=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots \!$

Les formules de ce type, maintenant connues sous le nom de formules de Machin, ont été utilisés pour battre plusieurs records de décimales connues de π, et demeurent aujourd'hui les formules les plus connues pour calculer π grâce à des ordinateurs. Un record remarquable est détenu par le calculateur prodigue Johann Dase qui, en 1844, à l'aide d'une formule de Machin, a calculé 200 décimales de π de tête, à la demande de Gauss. La meilleure valeur obtenue à la fin du XIX^e siècle est due à William Shanks, qui a passé 15 ans à calculer 707 décimales de π, bien qu'à cause d'une erreur, seules les 527 premières étaient correctes. De nos jours, pour éviter de telles erreurs, les calculs sont souvent effectués deux fois, avec deux formules différentes. Si les résultats sont les mêmes, il semble que le résultat soit correct.

Les avancées théoriques du XVIII^e siècle ont amené les mathématiciens à s'interroger sur la nature de π, qui ne peut pas être découverte uniquement grâce au calcul numérique. Johann Heinrich Lambert a prouvé l'irrationalité de π en 1761 et Adrien-Marie Legendre a prouvé que π² aussi était irrationnel. Lorsque Leonhard Euler a résolu le fameux problème de Bâle, trouvant la valeur exacte de

$\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots \!$

qui est π²/6, il a établi une connexion profonde entre π et les nombres premiers. Legendre et Euler ont tous les deux pensé que π était un nombre transcendant, ce qui a finalement été prouvé en 1882 par Ferdinand von Lindemann.

Origine de la notation

C'est au cours du XVIII^e siècle siècle que s'établit l'usage de la lettre grecque « π », première lettre des mots grecs περιφέρεια (périphérie) et περίμετρος (périmètre, c'est-à-dire circonférence) pour le rapport de la circonférence du cercle sur son diamètre.

Dès le XVII^e siècle siècle certains mathématiciens utilisent la notation π/δ où π désigne la circonférence et δ le diamètre. Le premier a utiliser simplement π est William Jones dans son livre A New Introduction to Mathematics publié en 1706, à propos du calcul astucieux de ce nombre par la série de son ami Machin. Les mathématiciens continuent cependant d'utiliser d'autres notations. Parmi ceux-ci Euler se met à la notation de Jones dans sa correspondance à partir de 1736. Il l'adopte dans son livre Introductio in analysin infinitorum publié en 1748, ce qui eut certainement une grande influence. La notation finit par s'imposer vers la fin du XVIII^e siècle.

Ère informatique

Alors que quelques dizaines de décimales de π sont largement suffisantes pour les calculs pratiques qu'effectue un physicien, la conquête des décimales du nombre π n'a pas cessé avec l'arrivée des ordinateurs, qui ont permis de calculer un très grand nombre de ces décimales.

En 1949, à l'aide de l'ENIAC, John von Neumann a obtenu 2037 décimales de π, suite à un calcul qui a duré 70 heures. Des milliers de décimales supplémentaires ont été trouvées au cours des décennies suivantes, l'étape du million de chiffres ayant été passée en 1973. Les progrès n'ont pas seulement été dus aux ordinateurs de plus en plus rapides, mais aussi aux nouveaux algorithmes utilisés. L'une des avancées les plus significatives a été la découverte de la transformée de Fourier rapide dans les années 1960, qui a permis aux ordinateurs de manipuler rapidement de très grands nombres.

Au début du XX^e siècle, le mathématicien indien Srinivasa Ramanujan a trouvé de nombreuses nouvelles formules faisant intervenir π ; certaines d'entre elles sont remarquables par leur élégance et leur profondeur mathématique. L'une de ces formules est la série suivante :

${\frac {1}{\pi }}={\frac {2{\sqrt {2}}}{9801}}\sum _{k=0}^{\infty }{\frac {(4k)!(1103+26390k)}{(k!)^{4}396^{4k}}}\!$

La formule ci-dessous, possédant un lien étroit avec celle énoncée ci-dessus, a été découverte par David et Gregory Chudnovsky en 1987 :

${\frac {426880{\sqrt {10005}}}{\pi }}=\sum _{k=0}^{\infty }{\frac {(6k)!(13591409+545140134k)}{(3k)!(k!)^{3}(-640320)^{3k}}}\!$

Cette formule donne 14 nouvelles décimales de π à chaque terme. Vers la fin des années 1980, les frères Chudnovsky l'ont utilisé pour battre plusieurs records de décimales de π calculées. Elle demeure la formule la plus utilisée pour calculer π sur des ordinateurs personnels.

Lemniscate de Bernoulli

Alors que les séries permettent d'obtenir des valeurs approchées de π avec un taux de précision supplémentaire à chaque terme qui est constant, il existe des algorithmes itératifs qui multiplient le nombre de décimales correctes à chaque étape, avec cependant l'inconvénient que chaque étape demande généralement un calcul « coûteux ». Une grande avancée a eu lieu en 1975 lorsque Richard Brent et Eugene Salamin ont découvert indépendamment l'algorithme Salamin-Brent, qui double le nombre de décimales correctes à chaque étape. Il s’appuie sur un vieux résultat pressenti puis démontré par Gauss. En 1818, celui-ci démontre le lien existant entre la moyenne arithmético-géométrique de 1 et √2 (M(1,√2)), la longueur de la lemniscate de Bernoulli et π. La longueur de la lemniscate est $L=2\varpi r$ où r représente la distance OA entre le centre et un sommet de la lemniscate et où $\varpi$ est la constante de la lemniscate. Si on note G, la constante de Gauss, c’est-à-dire l’inverse de M(1,√2) alors

$\varpi =\pi G$

Salamin et Brent ont utilisé ce résultat pour construire l'algorithme qui porte leur nom, et grâce auquel la conquête des décimales de π va alors avancer conjointement avec celle des décimales de √2.

L'algorithme consiste à poser

$a_{0}=1\quad \quad \quad b_{0}={\frac {1}{\sqrt {2}}}\quad \quad \quad t_{0}={\frac {1}{4}}\quad \quad \quad p_{0}=1\!$,

puis à définir les relations de récurrence suivantes

$a_{n+1}={\frac {a_{n}+b_{n}}{2}}\quad \quad \quad b_{n+1}={\sqrt {a_{n}b_{n}}}\!$

$t_{n+1}=t_{n}-p_{n}(a_{n}-a_{n+1})^{2}\quad \quad \quad p_{n+1}=2p_{n}\!$

et enfin à calculer ces termes jusqu'à ce que a_n et b_n soient assez proches. On a alors une valeur approchée de π donnée par

$\pi \approx {\frac {(a_{n}+b_{n})^{2}}{4t_{n}}}.\!$

En utilisant cet algorithme, seuls 25 termes sont nécessaires pour calculer 45 millions de décimales. Un algorithme similaire qui quadruple la précision à chaque étape a été trouvé par Jonathan et Peter Borwein. C'est grâce à ces méthodes qu'en 1999, Yasumasa Kanada et son équipe ont battu le record du nombre de décimales de π qui datait de 1980, en atteignant les 206 158 430 000 chiffres. Fabrice Bellard a annoncé, le 31 décembre 2009, avoir trouvé plus de 2 699 999 990 000 chiffres après la virgule à l’aide de son ordinateur personnel, soit 123 milliards de plus que le précédent record . Les calculs ont pris 131 jours. Le précédent record était de 2 576 980 370 000 chiffres, détenu par Daisuke Takahashi et son T2K-Tsukuba System, un superordinateur de l'université de Tsukuba, au nord-est de Tokyo.

Récemment, la formule BBP, découverte par Simon Plouffe, a fait de nouveau progresser la connaissance de π. La formule,

$\pi =\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}-{\frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right),$

est remarquable car elle permet de calculer n'importe chiffre de l'écriture de π en base hexadécimale ou binaire, sans calculer les précédents. Entre 1998 et 2000, le projet de calcul distribué PiHex a utilisé une variante de la formule BBP due à Fabrice Bellard pour calculer le 1 000 000 000 000 000 chiffre en binaire de π, qui s'est révélé être 0.

Si une formule de la forme

$\pi =\sum _{k=0}^{\infty }{\frac {1}{b^{ck}}}{\frac {p(k)}{q(k)}},$

était trouvée, avec b et c des entiers positifs et p et q des polynômes de degrés fixés à coefficients entiers (comme pour la formule BBP ci-dessus), ce serait l'un des moyens les plus efficaces pour calculer n'importe quel chiffre dans l'écriture de π en base b^c sans avoir à calculer les précédents, en un temps dépendant uniquement du nombre de termes de la série calculé et du degré des polynômes.

En 2006, Simon Plouffe a trouvé plusieurs formules faisant intervenir π. En posant q = e^π (constante de Gelfond), on a

${\frac {\pi }{24}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\left({\frac {3}{q^{n}-1}}-{\frac {4}{q^{2n}-1}}+{\frac {1}{q^{4n}-1}}\right)$

${\frac {\pi ^{3}}{180}}=\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}\left({\frac {4}{q^{n}-1}}-{\frac {5}{q^{2n}-1}}+{\frac {1}{q^{4n}-1}}\right)$

ainsi que

$\pi ^{k}=\sum _{n=1}^{\infty }{\frac {1}{n^{k}}}\left({\frac {a}{q^{n}-1}}+{\frac {b}{q^{2n}-1}}+{\frac {c}{q^{4n}-1}}\right)$

où k est un nombre impair, et a, b, c sont des nombres rationnels.

Culture populaire

Eventuellement reprendre les trucs existants.

Voir aussi

Liens externes

• La salle $\pi$ du Palais de la découverte