Théorème de Kosnita

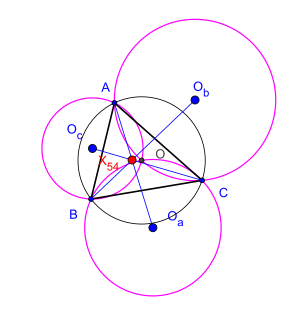
Dans la géométrie moderne du triangle, le théorème de Kosnita est une propriété de certains cercles associés à un triangle quelconque.

Soit $ABC$ un triangle, $O$ le centre de son cercle circonscrit et $O_{a},O_{b},O_{c}$ les centres des cercles circonscrits des triangles $OBC$ , $OCA$ et $OAB$ respectivement. Le théorème affirme que les trois droites $AO_{a}$ , $BO_{b}$ et $CO_{c}$ sont concourantes. Ce résultat a été établi par le mathématicien roumain Cezar Coşniţă (ro) (1910-1962)^[1], mais aurait été d'abord remarqué par Joseph Neuberg dans son Mémoire sur le tétraèdre en 1884^[2]^,^[3].

Ce point de concurrence est depuis appelé point de Kosnita du triangle, nom donné par John Rigby, et le triangle $O_{a}O_{b}O_{c}$ appelé triangle de Kosnita. Le nombre de Kimberling du point de Kosnita est $X(54)$ ^[4].

Propriétés[modifier | modifier le code]

Le point de Kosnita est le conjugué isogonal du centre du cercle d'Euler^[5]^,^[6]. Ses coordonnées trilinéaires sont done les inverses de celle du centre du cercle d'Euler, soit :

\mathrm {sec} (B-C):\mathrm {sec} (C-A):\mathrm {sec} (A-B)

On note K_A, l'image du point de Kosnita par la symétrie d'axe (BC), et on construit de façon cyclique K_B et K_C. Ensuite, on construit K_A', l'image du point de Kosnita par symétrie de centre le milieu de [K_BK_C], puis de même K_B' et K_C'. Alors (AK_A') est perpendiculaire à (BC), (BK_B') est perpendiculaire à (CA), et (CK_C') est perpendiculaire à (AB). On en déduit que les triangles ABC et K_A'K_B'K_C' sont homologues par rapport à l'orthocentre du triangle de référence.

Tout triangle et son triangle de Kosnita sont orthologiques.

Extensions[modifier | modifier le code]

Ce théorème est un cas particulier d'un théorème de Thanh Oai Dao sur six centres circonscrits associé à un hexagone inscriptible (dont les six sommets sont cocycliques^[7]^,^[8]^,^[9]^,^[10]^,^[11]^,^[12]^,^[13]).

Références[modifier | modifier le code]

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Kosnita's theorem » (voir la liste des auteurs).

↑ (ro) Ion Pătraşcu, « A generalization of Kosnita's theorem » [PDF], 2010
↑ Jean-Louis Aymé, « Le point de Cézar Kosnitza » [archive] [PDF]
↑ Joseph Neuberg, Mémoire sur le tétraèdre, Bruxelles, Hayez, 1884 (lire en ligne)
↑ (en) Clark Kimberling, « X(54) = Kosnita Point », sur Encyclopedia of Triangle Centers, 2014
↑ (en) Darij Grinberg, « On the Kosnita Point and the Reflection Triangle », Forum Geometricorum, vol. 3,‎ 2003, p. 105–111 (ISSN 1534-1178, lire en ligne [PDF])
↑ (en) John Rigby, « Brief notes on some forgotten geometrical theorems », Mathematics and Informatics Quarterly, vol. 7,‎ 1997, p. 156-158.
↑ (en) Nikolaos Dergiades, « Dao's Theorem on Six Circumcenters associated with a Cyclic Hexagon », Forum Geometricorum, vol. 14,‎ 2014, p. 243–246 (ISSN 1534-1178, lire en ligne).
↑ (en) Telv Cohl, « A purely synthetic proof of Dao's theorem on six circumcenters associated with a cyclic hexagon », Forum Geometricorum, vol. 14,‎ 2014, p. 261–264 (ISSN 1534-1178, lire en ligne).
↑ (en) Ngo Quang Duong, « Some problems around the Dao's theorem on six circumcenters associated with a cyclic hexagon configuration », International Journal of Computer Discovered Mathematics, vol. 1,‎ juin 2016, p. 25-39 (ISSN 2367-7775, lire en ligne)
↑ (en) Clark Kimberling, « X(3649) = KS(INTOUCH TRIANGLE) », 2014
↑ (en) Nguyễn Minh Hà, « Another Purely Synthetic Proof of Dao's Theorem on Sixcircumcenters », Journal of Advanced Research on Classical and Modern Geometries, vol. 6,‎ 2017, p. 37–44 (ISSN 2284-5569, lire en ligne)
↑ (en) Nguyễn Tiến Dũng, « A Simple proof of Dao's Theorem on Sixcircumcenters », Journal of Advanced Research on Classical and Modern Geometries, vol. 6,‎ 2017, p. 58–61 (ISSN 2284-5569, lire en ligne)
↑ (en) Nguyen Ngoc Giang, « The extension from a circle to a conic having center: The creative method of new theorems », International Journal of Computer Discovered Mathematics,‎ 2016, p. 21-32 (lire en ligne).

Voir aussi[modifier | modifier le code]

Liens externes[modifier | modifier le code]

(en) Eric W. Weisstein, « Kosnita Theorem », sur MathWorld
(en) Eric W. Weisstein, « Kosnita Point », sur MathWorld

Portail de la géométrie

[patrascu-1] (ro) Ion Pătraşcu, « A generalization of Kosnita's theorem » [PDF], 2010

[2] Jean-Louis Aymé, « Le point de Cézar Kosnitza » [archive] [PDF]

[3] Joseph Neuberg, Mémoire sur le tétraèdre, Bruxelles, Hayez, 1884 (lire en ligne)

[kimberlingX54-4] (en) Clark Kimberling, « X(54) = Kosnita Point », sur Encyclopedia of Triangle Centers, 2014

[grinberg2003-5] (en) Darij Grinberg, « On the Kosnita Point and the Reflection Triangle », Forum Geometricorum, vol. 3,‎ 2003, p. 105–111 (ISSN 1534-1178, lire en ligne [PDF])

[rigby1997-6] (en) John Rigby, « Brief notes on some forgotten geometrical theorems », Mathematics and Informatics Quarterly, vol. 7,‎ 1997, p. 156-158.

[dergiadesDao6CCCH-7] (en) Nikolaos Dergiades, « Dao's Theorem on Six Circumcenters associated with a Cyclic Hexagon », Forum Geometricorum, vol. 14,‎ 2014, p. 243–246 (ISSN 1534-1178, lire en ligne).

[cohlDao6CCCH-8] (en) Telv Cohl, « A purely synthetic proof of Dao's theorem on six circumcenters associated with a cyclic hexagon », Forum Geometricorum, vol. 14,‎ 2014, p. 261–264 (ISSN 1534-1178, lire en ligne).

[NgoQuangDuong-9] (en) Ngo Quang Duong, « Some problems around the Dao's theorem on six circumcenters associated with a cyclic hexagon configuration », International Journal of Computer Discovered Mathematics, vol. 1,‎ juin 2016, p. 25-39 (ISSN 2367-7775, lire en ligne)

[X3649-10] (en) Clark Kimberling, « X(3649) = KS(INTOUCH TRIANGLE) », 2014

[11] (en) Nguyễn Minh Hà, « Another Purely Synthetic Proof of Dao's Theorem on Sixcircumcenters », Journal of Advanced Research on Classical and Modern Geometries, vol. 6,‎ 2017, p. 37–44 (ISSN 2284-5569, lire en ligne)

[12] (en) Nguyễn Tiến Dũng, « A Simple proof of Dao's Theorem on Sixcircumcenters », Journal of Advanced Research on Classical and Modern Geometries, vol. 6,‎ 2017, p. 58–61 (ISSN 2284-5569, lire en ligne)

[13] (en) Nguyen Ngoc Giang, « The extension from a circle to a conic having center: The creative method of new theorems », International Journal of Computer Discovered Mathematics,‎ 2016, p. 21-32 (lire en ligne).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

v · m Triangles
Description	Sommet Apex Côté Angle Base
Types	Triangle équilatéral Triangle isocèle Triangle d'or Triangle rectangle Angle droit Cathète Hypoténuse Triangle de Kepler Triangle obtusangle Triangle acutangle Triangle isocèle rectangle Triangle pseudo-rectangle Triangle scalène Triangle de Héron
Points remarquables (Nombre de Kimberling)	Centres : Centre du cercle inscrit Centre de gravité Centre du cercle circonscrit Orthocentre Centre du cercle d'Euler Centre du cercle de Spieker Points de Brocard Points de Feuerbach Point de Fermat ou Point de Torricelli Point de Longchamps Point de Miquel Point de Gergonne Point de Nagel Point de Vecten Points isogonaux Points isodynamiques Point de Lemoine Points de Terquem Points de Napoléon Mittenpunkt
Droites remarquables	Cévienne Hauteur Médiane Bissectrice Médiatrice Droite de Brocard Droite d'Euler Droite de Lemoine Droite de Newton Droite de Simson (ou droite de Wallace) Droite de Steiner Ménélienne Symédiane Axe orthique Droite centrale
Cercles remarquables	Cercle circonscrit Cercle exinscrit Cercle inscrit Cercle d'Euler Cercle d'Apollonius Cercles de Lemoine Cercle de Longchamps Cercle de Miquel Cercle de Taylor Cercle de Tucker Cercle podaire Cercle de Brocard Cercle de Spieker Cercle de Fuhrmann Cercles de Johnson Cercle pédal
Triangles remarquables	Triangle de Bevan Triangle de Feuerbach Triangle de Gergonne Triangle de Morley Triangle de Nagel Triangle inscrit de périmètre minimal (Problème de Fagnano) Triangle médian Triangle orthique Triangle podaire Triangle tangentiel Triangle de Fuhrmann
Courbes remarquables	Deltoïde de Steiner Coniques Conique inscrite de Serret (ou de MacBeath) Conique orthique Hyperbole de Kiepert Paraboles Parabole tritangente Parabole de Kiepert Ellipses Ellipse de Mandart Ellipse de Steiner Coniques circonscrites et inscrites à un triangle Cubiques
Théorèmes	Théorème de Pythagore Théorème de Thalès Théorème de Napoléon Théorème japonais de Carnot Théorème de Ménélaüs Théorème de Morley Théorème de Nagel Théorème de Neuberg Théorème de Hamilton Théorème d'Euler Théorème de Feuerbach Théorème de Viviani Avec des céviennes Théorème de Ceva Théorème de Gergonne Théorème de Stewart Théorème de Terquem Théorème de Routh Théorème de Jacobi Avec des cercles Théorème des six cercles Théorème des trois cercles de Miquel
Relations entre triangles	Triangles isométriques Triangles semblables Inégalités dans le triangle
Résolution	Loi des cosinus Loi des sinus Loi des tangentes Loi des cotangentes Aire Formule de Héron