Logarithme népérien
| Notation | |
|---|---|
| Réciproque | |
| Dérivée | |
| Primitives |
| Ensemble de définition | |
|---|---|
| Ensemble image |
| Limite en +∞ |
+∞ |
|---|
| Asymptotes | |
|---|---|
| Zéros |
1 |
Le logarithme népérien, ou logarithme naturel, ou encore jusqu'au XXe siècle logarithme hyperbolique, transforme, comme les autres fonctions logarithmes, les produits en sommes. L'utilisation de telles fonctions permet de faciliter les calculs comprenant de nombreuses multiplications, divisions et élévations à des puissances rationnelles. Il est souvent noté ln().
Le logarithme naturel ou népérien est dit de base e car ln(e) = 1.
Le logarithme népérien d'un nombre x peut également être défini comme la puissance à laquelle il faut élever e pour obtenir x. La fonction logarithme népérien est donc la bijection réciproque de la fonction exponentielle. C'est également la primitive définie sur les réels strictement positifs et qui s'annule en 1 de la fonction inverse x ↦ 1x.
Cette fonction fut notée l. ou l, dès le début du XVIIIe siècle[1], et jusque dans la première moitié du XIXe siècle[2], puis log.[3] ou log[4] dès la fin du XVIIIe siècle, puis Log pour la différencier de la fonction log (logarithme de base quelconque, ou plus particulièrement logarithme décimal)[5], ou encore logh (« logarithme hyperbolique »)[6], avant que ne tente de s'imposer la notation préconisée par les normes AFNOR de 1961[7] et ISO 80000-2[8] : la notation ln. Avec un succès cependant très relatif : la notation log est encore aujourd'hui utilisée dans plusieurs branches des mathématiques, et tout particulièrement en théorie des nombres[9], ainsi que dans plusieurs langages de programmation, comme C, C++, SAS, R, MATLAB, Mathematica, Fortran, et BASIC.
Historique[modifier | modifier le code]

Ce logarithme est appelé népérien, en hommage au mathématicien écossais John Napier qui établit les premières tables logarithmiques (lesquelles ne sont en fait pas des tables de logarithmes népériens[10]). On date en général l'origine des logarithmes népériens en 1647, lorsque Grégoire de Saint-Vincent travaille sur la quadrature de l'hyperbole et démontre que la fonction obtenue vérifie la propriété d'additivité des fonctions logarithmes. Saint-Vincent ne voit cependant pas de lien avec les logarithmes de Napier, et c'est son disciple Alphonse Antoine de Sarasa qui l'expliquera en 1649[11]. Le logarithme népérien s'est tout d'abord appelé « logarithme hyperbolique », en référence à l'aire sous l'hyperbole qu'il représente[12]. L'appelation « logarithme naturel », due à Pietro Mengoli en 1659[13], est reprise en 1668 dans une note de Nicolaus Mercator sur la série qui porte son nom[14]. Cette série, exploitée par Newton en 1671[15], permet de calculer assez simplement les valeurs du logarithme de Grégoire de Saint-Vincent[16]. Le calcul des autres logarithmes apparaît alors bien compliqué et, naturellement, celui de Grégoire de Saint-Vincent devient alors le logarithme le plus naturel.

La fonction logarithme naturel comme primitive de la fonction inverse[modifier | modifier le code]
La fonction x ↦ 1x est continue sur ]0, +∞[. Elle admet donc des primitives dont une seule s'annule en 1. Cette primitive est appelée logarithme naturel et est donc définie par :
Étude de la fonction[modifier | modifier le code]
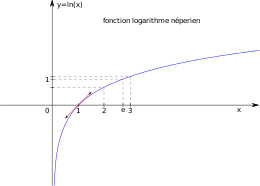
- La fonction logarithme naturel est définie et dérivable (donc continue) sur ]0, +∞[ et pour tout réel x strictement positif,
- Puisque cette dérivée est strictement positive, le logarithme naturel est strictement croissant.
- Puisque cette dérivée est strictement décroissante, le logarithme naturel est strictement concave.
- Les limites de la fonction aux bornes de son intervalle de définition sont :
C'est donc une bijection de ]0, +∞[ sur ℝ. - Son nombre dérivé au point 1 (qui donne la pente de la tangente au graphe au point de coordonnées (1, 0)) est :
Propriétés algébriques[modifier | modifier le code]
Le logarithme naturel vérifie la même équation fonctionnelle que toute fonction logarithme. C'est une fonction continue vérifiant, pour tous réels x et y strictement positifs,
En effet, pour y > 0 fixé, la fonction x ↦ ln(xy) (définie sur ]0, +∞[) a la même dérivée que le logarithme naturel, donc en diffère d'une constante réelle k : ln(xy) = ln(x) + k, avec k = ln(y) puisque ln(1y) = ln(1) + k = k.
De cette propriété algébrique, on déduit les suivantes, pour tous réels a et b strictement positifs :
Puis par continuité
Le fait que toutes les fonctions logarithmes soient proportionnelles entre elles permet d'obtenir, pour tout réel a strictement positif, le logarithme de base a en fonction du logarithme népérien :
La fonction logarithme naturel comme réciproque de la fonction exponentielle[modifier | modifier le code]
L'étude de la fonction logarithme naturel a montré que c'est une bijection de ]0, +∞[ dans ℝ. Sa bijection réciproque, de ℝ dans ]0, +∞[, coïncide avec la fonction exponentielle, puisqu'elle est sa propre dérivée et prend la valeur 1 en 0. Ceci fournit une définition possible de la fonction exponentielle à partir du logarithme. Inversement, on aurait pu définir le logarithme comme la bijection réciproque de l'exponentielle et vérifier alors sa caractérisation ci-dessus.
Autrement dit :
ce qui se résume en :
et permet de résoudre des équations dans lesquelles l'inconnue apparaît en exposant.
Cette relation permet d'exprimer toutes les autres fonctions exponentielles de base un réel a strictement positif par (pour tout réel x) :
Cette définition coïncide évidemment avec celle de ar pour r rationnel.
Développement en série[modifier | modifier le code]


La fonction n'admet pas de développement en série de Taylor, ni même de Laurent autour de .
C'est Nicolaus Mercator qui a été le premier à proposer le développement en série entière de ; le rayon de convergence de ce développement est 1. On a donc la série de Taylor :
(Voir aussi Fonction hypergéométrique#Cas particuliers.)
D'après la formule de Taylor-Lagrange[17] ou le théorème de convergence radiale d'Abel, ce développement est encore valide pour x = 1. On obtient ainsi la somme de la série harmonique alternée.
D'autre part, notons que Leonhard Euler a hardiment appliqué ce développement à x = –1[18]. Sans se soucier de la convergence, il montre que la série harmonique est le logarithme naturel de 11 – 1, c'est-à-dire de l'infini. Aujourd'hui on formalise cette remarque d'Euler par : « la série harmonique tronquée en N est proche du logarithme de N lorsque N est grand » ; plus précisément, les différences entre somme partielle de la série harmonique et logarithme naturel convergent vers la constante d'Euler-Mascheroni.
Pour obtenir une meilleure vitesse de convergence, on peut en déduire :
qui se réécrit :
Propriétés complémentaires[modifier | modifier le code]
Étude des limites[modifier | modifier le code]
Les limites suivantes permettent de déterminer les croissances comparées du logarithme naturel et d'une fonction puissance quelconque :
Dérivée logarithmique[modifier | modifier le code]
Pour toute fonction réelle dérivable u, la fonction composée ln∘|u| (définie en tout point où u ne s'annule pas) est dérivable, de dérivée
Cette dérivée s'appelle la dérivée logarithmique de la fonction u. Elle représente une variation instantanée relative. C'est donc une mesure utile tant en économie qu'en calcul d'erreur. Elle permet d'autre part un calcul plus simple de la dérivée de fonctions données sous forme de produits, quotients ou puissances.
Primitive[modifier | modifier le code]
En appliquant la formule d'intégration par parties au produit des fonctions et , on obtient :
- .
D'après le théorème fondamental de l'analyse, les primitives de sont donc les fonctions de la forme
- ,
la plus simple étant la fonction .
La fonction logarithme naturel comme fonction de la variable complexe[modifier | modifier le code]
La question de savoir s'il est possible de prolonger le logarithme naturel (c'est-à-dire de le définir sur un ensemble plus grand que ]0, +∞[) s'est posée dès la seconde moitié du XVIIe siècle avec les développements en série des fonctions. Le problème est qu'il n'existe aucune fonction univoque continue sur ℂ*, possédant la propriété algébrique des fonctions logarithmes et coïncidant sur ]0, +∞[ avec la fonction logarithme népérien réelle.
On peut cependant définir le logarithme d'un nombre négatif en posant, pour tout réel a strictement positif, ln(–a) = ln(a) + iπ, mais la fonction ainsi définie n'a pas les propriétés algébriques de la fonction logarithme népérien réelle. On peut la rencontrer lorsqu'on travaille avec une calculatrice traitant les nombres complexes : si l'on étudie la fonction x ↦ |ln(x)|, la calculatrice peut être amenée à définir cette fonction sur ℝ* en interprétant la valeur absolue comme un module :
- pour a réel strictement positif.
Notes et références[modifier | modifier le code]
- Voir par exemple (la) Leonhard Euler, « Variae observationes circa series infinitas », Commentarii academiae scientarum Petropolitanae, vol. 9, , p. 160-188 ; aussi dans Opera Omnia, Series Prima, Opera Mathematica, Volumen Quartum Decimum, Teubner, 1925.
- Voir par exemple Augustin Cauchy, Exercices d'analyse et de physique mathématique, vol. 3, p. 379, lire en ligne sur Google Livres.
- Voir par exemple Adrien-Marie Legendre, Essai sur la théorie des nombres, Paris, Duprat, an VI (1797 ou 1798).
- Voir par exemple (de) Edmund Landau, Handbuch der Lehre von der Verteilung der Primzahlen, Berlin, 1909 (2e éd. par Chelsea, New York, 1953).
- Voir les manuels scolaires en France jusqu'en 1972. Ou par exemple : Nikolaï Piskounov, Calcul différentiel et intégral, 5e éd., 1972, Éditions Mir, Moscou III.10 p. 91.
- Voir par exemple (en) L. B. W. Jolley, Summation of Series, 2e édition (révisée), Dover Publications, New York, 1961, lire en ligne.
- NF X 02-1 01 selon les tables numériques de J. Laborde, p. VI, 1976.
- ISO 80000-2:2009, Organisation internationale de normalisation.
- Voir par exemple cette note de (en) G. H. Hardy et E. M. Wright, An Introduction to the Theory of Numbers (1re éd. 1938) [détail des éditions] (6e éd., Oxford, 2008, 1.7) « log x is, of course the 'Napierian' logarithm of x, to base e. 'Common' logarithms have no mathematical interest. »
- A. Dahan-Dalmedico et J. Peiffer, Une histoire des mathématiques : Routes et dédales, [détail des éditions], p. 214.
- Jean-Pierre Le Goff, « De la méthode dite d'exhaustion - Grégoire de Saint Vincent », dans La démonstration mathématique dans l'histoire, IREM de Besançon.
- Simone Trompler, « L'histoire des logarithmes », ULB, , p. 11.
- (la) Mengoli, Geometriae speciosae Elementa. Références et liens collectés par (en) Jeff Miller, « Earliest Known Uses of Some of the Words of Mathematics — Natural logarithm ».
- (en) Mercator, « Some Illustration of the Logarithmotechnia », Philosophical Transactions, vol. 3, no 38, , p. 759-764 (lire en ligne).
- Méthode de Newton pour le calcul des logarithmes naturels, La méthode des fluxions et des suites infinies sur Gallica, p. 102-105.
- Trompler 2002, p. 12.
- S. Balac et L. Chupin, Analyse et algèbre : cours de mathématiques de deuxième année avec exercices corrigés et illustrations avec Maple, PPUR, (lire en ligne), p. 56.
- (la) Leonhard Euler, Introductio in analysin infinitorum, tome 1, Bousquet, Lausanne, 1748, exemple 1, p. 228 ; aussi dans Opera Omnia, Series Prima, Opera Mathematica, vol. 8, Teubner, 1922.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Exemple d'application du théorème de Gelfond-Schneider : ln(3)/ln(2) est transcendant
- Logarithme népérien de deux
- Logarithme binaire
- Logarithme discret
- Logarithme intégral
- Fonction W de Lambert
Liens externes[modifier | modifier le code]
« Poser la modélisation comme question épistémologique pour l’introduction des propriétés des exponentielles dans les classes », conférence de Jean Dhombres : parties 1, 2 et 3
Une excellente vidéo en anglais expliquant l'origine des logarithmes naturels



















![{\displaystyle \forall x\in ]0,+\infty [\qquad f'(x)={\frac {1}{g'(f(x))}}={\frac {1}{g(f(x))}}={\frac {1}{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/667c3bcbe6223f2b342248ec2b5d2b5b946adddc)







![{\displaystyle {\begin{aligned}\forall x\in \left]-1,1\right[\quad \ln(1+x)&=-\sum _{n=1}^{\infty }{\frac {(-x)^{n}}{n}}\\&=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots \\&=x\left({\frac {1}{1}}-x\left({\frac {1}{2}}-x\left({\frac {1}{3}}-x\left({\frac {1}{4}}-x\left({\frac {1}{5}}-\cdots \right)\right)\right)\right)\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ec3adb4acb6548ed3d574dd39f2ca514ff8361a)
![{\displaystyle {\begin{aligned}\forall x\in \left]-1,1\right[\quad \ln \left({\frac {1+x}{1-x}}\right)&=2x\left({\frac {1}{1}}+{\frac {1}{3}}x^{2}+{\frac {1}{5}}x^{4}+{\frac {1}{7}}x^{6}+{\frac {1}{9}}x^{8}+\cdots \right)\\&=2x\left({\frac {1}{1}}+x^{2}\left({\frac {1}{3}}+x^{2}\left({\frac {1}{5}}+x^{2}\left({\frac {1}{7}}+x^{2}\left({\frac {1}{9}}+\cdots \right)\right)\right)\right)\right),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f2567ae10259ae27a185ea032d5005bc11f58a2)
![{\displaystyle \forall y\in \left]0,+\infty \right[\quad \ln(y)=2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {y-1}{y+1}}\right)^{2k+1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9123cb1037f3459b32bc2cc4f075cfc02e2f041)






