2-catégorie

En mathématiques, et plus particulièrement en théorie des catégories, une 2-catégorie est une catégorie avec des « morphismes entre les morphismes », c'est-à-dire que chaque « ensemble des morphismes » transporte la structure d'une catégorie. Une 2-catégorie peut être formellement définie comme étant une catégorie enrichie au-dessus de Cat (la catégorie des catégories petites et les foncteurs entre elles), avec la structure monoïdale donnée par le produit de deux catégories.

Définition

2-catégorie stricte

Composition verticale de deux 2-morphismes dans une 2-catégorie.

Composition horizontale de deux 2-morphismes dans une 2-catégorie.

Compatibilité entre les compositions horizontales et verticales de 2-morphismes.

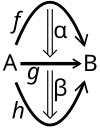
Une 2-catégorie (stricte) ${\mathcal {C}}$ est la donnée :

• d'une classe de 0-cellules (ou objets) ;
• pour tous objets A, B, d'une catégorie ${\mathcal {C}}(A,B)$. Les objets f, g : A → B de cette catégorie sont appelés 1-cellules (ou morphismes ou encore 1-morphismes) et les morphismes α : f ⇒ g sont appelés 2-cellules (ou 2-morphismes).

Les 1-morphismes peuvent être composés suivant les objets. Il s'agit de la composition usuelle des morphismes dans une catégorie.

Les 2-morphismes peuvent être composés de deux manières : suivant les objets et suivant les 1-morphismes. Ces deux compositions sont appelées respectivement composition horizontale et composition verticale.

La composition verticale est définie comme suit. Soient deux 0-cellules A et B, et trois 1-morphismes f, g, h : A → B. Soient les 2-morphismes α : f ⇒ g et β : g ⇒ h. Alors la composition verticale de α et β est le 2-morphisme β $\circ$ α : f ⇒ h, qui est la composition de morphismes au sens usuel dans la catégorie ${\mathcal {C}}(A,B)$.

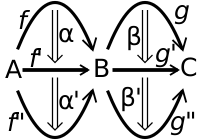
La composition horizontale est définie comme suit. Soient trois 0-cellules A, B et C, et quatre 1-morphismes f, g: A → B et f' , g' : B → C. Soient deux 2-morphismes α : f ⇒ g et β : f' ⇒ g' . On peut définir les composées de 1-morphismes f'f: A → C et g'g: A → C. Dans une 2-catégorie, on suppose qu'il existe un foncteur de ${\mathcal {C}}(B,C)\times {\mathcal {C}}(A,B)$ vers ${\mathcal {C}}(A,B)$, qui associe aux deux 2-morphismes α et β un 2-morphisme noté βα : f'f⇒ g'g. Cela se traduit par une relation de cohérence entre les compositions horizontale et verticale. Si on a quatre 2-morphismes α : f ⇒ f' , α' : f' ⇒ f", β : g ⇒ g' , β' : g' ⇒ g", alors on a (β' $\circ$ β)(α' $\circ$ α) = β'α' $\circ$ βα.

De plus, si id_A est le 1-morphisme identité de l'objet A et si Id_idA est le 2-morphisme identité de l'objet id_A dans la catégorie ${\mathcal {C}}(A,A)$, alors la composée horizontale de ce 2-morphisme par un 2-morphisme α est égal à α.

Bicatégorie

Une bicatégorie est une notion faible de 2-catégorie. L'associativité et la composition avec les morphismes identité dans la définition de 2-catégorie stricte sont satisfaites seulement à isomorphisme près.

Une bicatégorie ${\mathcal {C}}$ est la donnée :

• d'une classe de 0-cellules (ou objets) ;
• pour tous objets A, B, d'une catégorie ${\mathcal {C}}(A,B)$. Les objets f, g : A → B de cette catégorie sont appelés 1-cellules (ou morphismes ou encore 1-morphimes) et les morphismes α : f ⇒ g dont appelés 2-cellules (ou 2-morphismes).
• pour tout objet A, d'une 1-cellule 1_A, appelée morphisme identité ;
• pour tout objets A, B, C, d'un foncteur $\circ :{\mathcal {C}}(B,C)\times {\mathcal {C}}(A,B)\to {\mathcal {C}}(A,C)$ appelé composition horizontale ;
• pour tout objets A, B, d'un isomorphisme naturel ${\mathcal {C}}(A,B)\to {\mathcal {C}}(A,B)$, appelé uniteur ;
• pour tout objets A, B, C, D, d'un isomorphisme naturel appelé associateur ;

tels que

• les associateurs satisfont l'identité du pentagone ;
• les uniteurs satisfont l'identité du triangle.

S'il y a exactement une 0-cellule A, alors la définition est celle d'une structure monoïdale sur la catégorie ${\mathcal {C}}(A,A)$.

Exemple

• La catégorie des petites catégories est une 2-catégorie où les objets sont les catégories, les morphismes sont les foncteurs et les 2-morphismes sont les transformations naturelles.
• Toute 2-catégorie stricte est une bicatégorie dont les uniteurs et associateurs sont des identités.

Morphismes dans une 2-catégorie

Équivalence

Un morphisme f : A → B dans une 2-catégorie est appelé une équivalence s'il existe un morphisme g : B → A et des isomorphismes gf ≅ 1_A et fg ≅ 1_B.

Adjoint

Une adjonction dans une 2-catégorie consiste en la donnée de deux 1-cellules f : A → B et u : B → A et de deux 2-cellules η : 1_A → uf et ε : fu → 1_B satisfaisant les équations des triangles, c'est-à-dire les compositions

$f{\stackrel {f\eta }{\to }}fuf{\stackrel {\epsilon f}{\to }}f$

et

$u{\stackrel {\eta u}{\to }}ufu{\stackrel {u\epsilon }{\to }}u$

sont des identités. On dit que f est un adjoint à gauche de u.

Si les deux 2-cellules sont inversibles, on parle d'équivalence adjointe.

Pleinement fidèle, fidèle, conservatif

Un morphisme f: A → B dans une 2-catégorie ${\mathcal {C}}$ est dit fidèle (respectivement pleinement fidèle, conservatif) si pour tout objet C dans ${\mathcal {C}}$, le foncteur induit

${\mathcal {C}}(C,A)\to {\mathcal {C}}(C,B)$

est fidèle (respectivement pleinement fidèle, conservatif).

Discret

Un morphisme f: A → B dans une 2-catégorie ${\mathcal {C}}$ est dit discret s'il est fidèle et conservatif.

Morphismes entre deux 2-catégories

On s'intéresse ici aux relations entre différentes 2-catégories.

Équivalence de 2-catégories

Une équivalence de 2-catégories C et D consiste en la donnée de :

• deux pseudo-foncteurs F : C → D, G : D → C ;
• deux transformations pseudo-naturelles G∘F → Id, F∘G → Id qui sont des équivalences, c'est-à-dire admettant des transformations pseudo-naturelles formant leurs inverses à isomorphisme près.

Monades

Une monade dans une 2-categorie consiste en la donnée d'une 0-cellule X, d'une 1-cellule t : X → X et de deux 2-cellules μ : t² ⇒ t et η : id_X ⇒ t, satisfaisant les trois mêmes axiomes qu'une monade usuelle (dans la 2-catégorie des catégories).

• Une adjonction dans une 2-catégorie donne naissance à une monade.

Voir aussi

• Théorie des catégories supérieuresThéorie des catégories supérieures

Références

• (en) Generalised Algebraic Models, Claudia Centazzo
• (en) « 2-category » sur ncatlab.org
• (en) Basic bicategories, Tom Leinster
• (en) A 2-categories companion, Steve Lack

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « 2-category » (voir la liste des auteurs).