Résonance
La résonance est un phénomène selon lequel certains systèmes physiques (électriques, mécaniques, etc.) sont sensibles à certaines fréquences. Un système résonant peut accumuler une énergie, si celle-ci est appliquée sous forme périodique, et proche d'une fréquence dite « fréquence de résonance ». Soumis à une telle excitation, le système va être le siège d'oscillations de plus en plus importantes, jusqu'à atteindre un régime d'équilibre qui dépend des éléments dissipatifs du système, ou bien jusqu'à une rupture d'un composant du système.
Si on soumet un système résonant à un degré de liberté, non plus à une excitation périodique, mais à une percussion (pour les systèmes mécaniques), ou à une impulsion (pour les systèmes électriques), alors le système sera le siège d'oscillations amorties, sur une fréquence proche de sa fréquence propre et retournera progressivement à son état stable.
Les domaines où la résonance intervient sont innombrables : balançoire enfantine, mais aussi résonances acoustiques de la voix parlée ou chantée et des instruments de musique, la résonance des marées, la résonance orbitale en astronomie, la résonance de la membrane basilaire dans le phénomène d'audition, les résonances dans des circuits électroniques et, pour finir : tous les systèmes, montages, pièces mécaniques sont soumis au phénomène de résonance. Les systèmes abstraits sont également soumis à des résonances : on peut, à titre d'exemple, citer la dynamique des populations. Dans le domaine du génie civil, on peut observer ce phénomène principalement dans les passerelles piétonnes soumises à des marches militaires, par exemple, ou, de façon plus générale, dans les constructions soumises à un séisme.
Notions de base[modifier | modifier le code]
Principe physique[modifier | modifier le code]

Un système susceptible d'entrer en résonance, c'est-à-dire susceptible d'amplifier sa réponse à certaines sollicitations cycliques entretenues, est un oscillateur. Un tel système a la particularité de pouvoir emmagasiner temporairement de l'énergie sous deux formes : potentielle ou cinétique. L'oscillation est le phénomène par lequel l'énergie du système passe d'une forme à l'autre, de façon périodique.
Dans un système mécanique, l'énergie alterne de la forme potentielle à la forme cinétique : par exemple un système masse sur ressort que l'on comprime (qu'on éloigne de sa position d'équilibre) acquerra une énergie potentielle qui sera restituée en énergie cinétique lors de sa détente. Puis, par inertie, le ressort s'allongera jusqu'à transformer entièrement l'énergie cinétique en énergie potentielle et ainsi de suite. S'ensuit un mouvement vibratoire plus ou moins amorti, au cours duquel la vitesse (donc l’énergie cinétique) est maximale au point d'équilibre et l'énergie potentielle maximale aux extrema d'élongation. Le phénomène dure jusqu'à ce que toute l’énergie doit dissipée par les phénomènes dissipatifs (amortissement).
Dans un circuit RLC, l'énergie est sous forme potentielle quand la tension est maximale aux bornes du condensateur. L'énergie est sous forme cinétique (ou magnétique) quand le courant est maximal dans la bobine (et la tension nulle sur le condensateur).
Si on injecte une énergie potentielle au moment où l'énergie potentielle déjà emmagasinée est maximale, l'énergie ainsi injectée s'ajoute à l'énergie déjà emmagasinée et l'amplitude de l'oscillation va augmenter, ainsi que l'énergie totale. De la même façon, si on injecte de l'énergie cinétique au moment où l'énergie cinétique est maximale, l'énergie totale augmentera. Si on apporte ainsi de l'énergie avec une périodicité égale (ou proche) de la périodicité propre du système, l'énergie totale va augmenter régulièrement. L'amplitude des oscillations du système va ainsi croître. L'exemple le plus simple est celui d'une balançoire : l'énergie de chaque poussée s'ajoute à l'énergie totale, à condition de pousser au bon moment…
Le phénomène de résonance n'est rien d'autre que cet effet d'accumulation de l'énergie en injectant celle-ci au moment où elle peut s'ajouter à l'énergie déjà accumulée, c'est-à-dire « en phase » avec cette dernière.
Amortissement[modifier | modifier le code]
Quand l'excitation aura cessé, le système résonant va être le siège d'oscillations amorties : il va revenir plus ou moins vite à son état d'équilibre stable. En effet, l'énergie de départ sera peu à peu absorbée par les éléments « dissipatifs » du système (amortisseur visqueux en mécanique, résistances en électricité...). Un système peu amorti sera le siège d'un grand nombre d'oscillations qui diminueront lentement avant de disparaître complètement.
Si on soumet un système peu amorti à une excitation périodique permanente selon sa fréquence de résonance, l'énergie ainsi apportée va s'accumuler lentement et se traduira par des oscillations de grande amplitude. En régime stabilisé, l'énergie apportée à chaque période est égale à l'énergie dissipée, ce qui explique la grande amplitude des oscillations du système peu amorti. L'énergie accumulée sera importante, mais un amortissement accru peut diminuer l'amplitude des oscillations, l'énergie dissipée par période est donc l'énergie accumulée.
En électricité, on peut chiffrer l'amortissement en définissant le « coefficient de surtension » ou la « sélectivité ».
Modes propres[modifier | modifier le code]
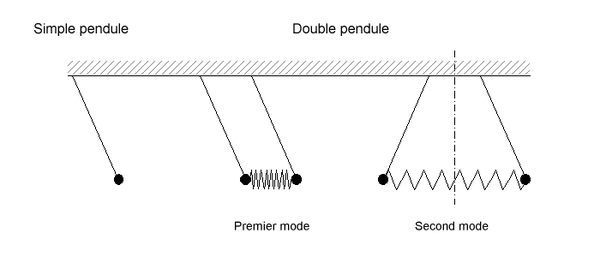
Implicitement, l'introduction concerne des systèmes à un degré de liberté ou supposés tels dont l'évolution est décrite par un seul paramètre fonction du temps. On rencontre de tels systèmes, entre autres, en mécanique avec le pendule simple ou le système masse-ressort, en électricité avec le circuit RLC. Leurs oscillations libres ne peuvent se produire qu'à une fréquence bien définie susceptible d'induire une résonance.
Si on couple deux pendules par un ressort, le système est alors décrit par les inclinaisons généralement distinctes des deux pendules. Ce système à deux degrés de liberté possède deux modes propres dans lesquels les pendules oscillent à la même fréquence. Toute oscillation libre est une somme des deux modes propres correspondants et, face à une excitation sinusoïdale, chacun d'eux peut engendrer une résonance. En supposant les deux pendules identiques, l'origine des deux types d'oscillation devient évidente. Dans un cas les pendules oscillent de concert, comme s'ils étaient liés par une barre rigide ; la fréquence propre du système est la même que celle du pendule simple. Dans l'autre, ils oscillent en opposition, comme si le milieu du ressort avait été fixé ; une moitié de ressort accroît donc la raideur associée à chacun d'eux, ce qui, comme il est précisé plus loin, augmente la fréquence propre.
Ces remarques se généralisent à des systèmes qui possèdent un nombre quelconque de degrés de liberté. La déformation d'une corde vibrante ou d'une poutre élastique est caractérisée par une infinité de positions ; il s'agit alors de systèmes continus à une infinité de degrés de liberté possédant une infinité de modes propres. Dans le cas de la corde sans raideur en flexion, les modes propres ont des formes sinusoïdales (pour plus de précisions, voir Onde sur une corde vibrante). La plus basse fréquence est alors appelée fréquence fondamentale tandis que les harmoniques ont des fréquences multiples de celle-ci ; le spectre est l'ensemble des fréquences propres.
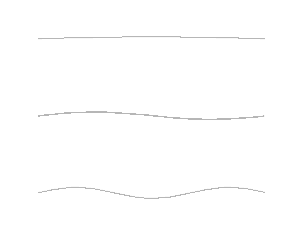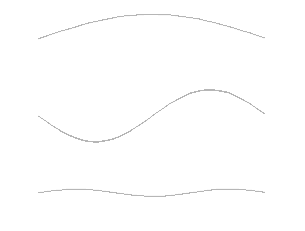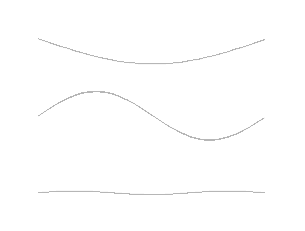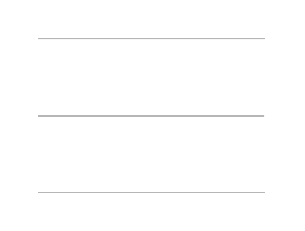
Généralement, l'importance relative de l'amortissement s'accroît à mesure que s'élève l'ordre des modes, ce qui fait qu'il est suffisant de s'intéresser aux tout premiers modes, dans les problèmes techniques si ce n'est en musique.
La représentation modale est pertinente dans le domaine des basses fréquences, c'est-à-dire pour les premiers modes propres (les modes sont classés traditionnellement par fréquences propres croissantes sur le spectre). Dans les domaines moyenne et haute fréquence, on utilise des méthodes adaptées à la densité spectrale élevée.
Les domaines moyenne fréquence et haute fréquence sont définis par la densité spectrale.
En effet, l'expression en fréquences n'a pas de sens pour définir ces domaines, une similitude sur un système physique modifie les fréquences propres mais le spectre reste semblable, à un facteur près.
Dans le cas de fréquences multiples, il existe un sous-espace propre donc les modes propres sont arbitraires dans ce sous espace.
Dans le cas de fréquences voisines (densité spectrale élevée), la représentation modale n'est pas robuste car de faibles perturbations du domaine physique vont entraîner un changement important des modes propres associés à ces fréquences.
Donc la représentation modale n'est pertinente que pour le domaine des basses fréquences, domaine défini par la densité spectrale.
Le domaine basse fréquence s'étendra jusqu'à quelques Hz en génie civil, jusqu'à des milliers de Hz pour de petites structures mécaniques.
Réponse à une excitation[modifier | modifier le code]
Dans un système oscillant à un degré de liberté, on constate que le rapport de l'amplitude X de la réponse à l'amplitude F de l'excitation dépend de la masse M (ou inertie ou, en électricité, auto-inductance), de la raideur K (ou inverse de la capacité) et de l'amortissement B (ou résistance) :
Cette formule montre, ce qui se généralise qualitativement à des systèmes beaucoup plus complexes, voire non linéaires, que la fréquence propre croît avec la raideur et décroît lorsque l'inertie augmente.
Quantitativement, pour un système linéaire, la généralisation se ferait en définissant un effort généralisé, en projetant les efforts extérieurs sur le mode concerné. Un mode n'est pas excitable sur les nœuds de vibration.
L'amplification ne varie pas seulement en fonction de la fréquence. Elle dépend également de l'amortissement du système : lorsque celui-ci décroît, l'amplification augmente dans une bande de fréquences de plus en plus étroite.
Ce phénomène d'amplification est mis à profit dans divers domaines pour séparer une fréquence déterminée de ses voisines.
À l'inverse, il peut être fréquemment à l'origine de dommages causés au système. Dans ce dernier cas, on cherche soit à l'atténuer en augmentant l'amortissement, soit à déplacer la fréquence propre en jouant sur l'inertie ou sur la raideur.
La synchronisation[modifier | modifier le code]
Christian Huygens a remarqué que deux horloges à balancier, placées sur la même cloison, synchronisaient leur mouvement ; il en a fourni l'explication. Le système composé des deux balanciers et de la cloison a deux fréquences voisines faiblement couplées, il possède par le couplage deux modes propres correspondant aux mouvements en phase et en opposition de phase des deux pendules : c'est sur le premier mode que se produit la synchronisation. On retrouve la synchronisation dans de nombreux phénomènes naturels : vols d'oiseau, clignotement des lucioles...
Utilisations de la résonance[modifier | modifier le code]
La résonance permet de trier certaines fréquences, mais ne produit pas d'énergie. Le résonateur accumule de l'énergie.
Le moteur deux temps[modifier | modifier le code]
Le pot d'échappement d'un moteur à deux temps a une forme bien particulière, calculée pour créer un phénomène de résonance qui améliore les performances du moteur en diminuant la consommation et la pollution. Cette résonance réduit partiellement les gaz imbrûlés et augmente la compression dans le cylindre.
Les instruments de musique[modifier | modifier le code]
Pour ce qui est des instruments à cordes frottées et à vent, la production du son consiste la plupart du temps en l'excitation d'un système oscillant (corde, colonne d'air) jusqu'à l'apparition d'un phénomène de résonance.
Les récepteurs radio[modifier | modifier le code]
Chaque station de radio émet une onde électromagnétique avec une fréquence bien déterminée. Pour la capter, le circuit RLC (résistance, inductance, capacité) est mis en vibration forcée, par l'intermédiaire de l'antenne qui capte toutes les ondes électromagnétiques arrivant jusqu'à elle. Pour écouter une seule station, on doit accorder la fréquence propre du circuit RLC avec la fréquence de l'émetteur désiré, en faisant varier la capacité d'un condensateur variable (opération effectuée en agissant sur le bouton de recherche des stations).
D'une façon générale, tous les systèmes de radiocommunications, qu'ils soient émetteur ou récepteur, utilisent des résonateurs pour « filtrer » les fréquences des signaux qu'ils traitent : circuit RLC, résonateurs à quartz, résonateurs céramique, etc.
La résonance magnétique nucléaire (RMN) et l'imagerie par résonance magnétique (IRM)[modifier | modifier le code]
En 1946, les deux américains Félix Bloch et Edward Mills Purcell découvrent indépendamment le phénomène de Résonance Magnétique Nucléaire[1],[2],[3] également appelé RMN (ce qui leur valut un prix Nobel de Physique). En plaçant un objet dans un champ magnétique et en l'excitant avec une onde radiofréquence de fréquence (de résonance) adéquate, on peut connaître, grâce à un signal qu’émet cet objet en retour, des détails sur sa composition chimique. Par la suite, en 1971, Richard Ernst sera primé pour son travail spectroscopie à haute résolution par RMN suivi du suisse Kurt Wüthrich en 2002 pour la détermination structurale en 3D des macromolécules en solution.
Fonctionnement simplifié de l'IRM[modifier | modifier le code]
En 1971, Raymond Damadian se rend compte que le signal émis par un tissu organique cancéreux est différent de celui qu’émet un tissu sain du même organe[4]. Deux ans plus tard, Paul Lauterbur traduit le signal en images à deux dimensions. Apparaît alors l’imagerie par résonance magnétique proprement dite.
L’IRM subira encore quelques évolutions : le britannique Peter Mansfield applique la RMN des objets à structure interne complexe. Il deviendra, grâce à ses expériences poussées, l’un des pionniers de l’Imagerie par Résonance Magnétique dans des applications médicales.
L'IRM utilise la résonance magnétique des protons d'un organisme pour fabriquer des images. Les protons des molécules d'eau réagissent de façon spécifique au champ magnétique ; le corps humain est composé en majorité d'eau. Placé dans un intense champ magnétique, on excite les protons des molécules d'eau à l'aide d'une émission électromagnétique (radio-fréquence) jusqu'à les mettre en résonance. Avec une antenne, on mesure l'énergie rendue par les protons lors de l'arrêt de l'excitation. Un ordinateur analyse et interprète les informations captées par l'antenne, en créant une image en trois dimensions.
Inconvénients de la résonance[modifier | modifier le code]
Automobiles[modifier | modifier le code]
Les automobilistes sont souvent irrités par les bruits parasites qui apparaissent à une certaine vitesse du véhicule ou de rotation du moteur. Certaines pièces mal amorties du moteur, ou de la carrosserie, entrent en résonance et émettent des vibrations sonores. L'automobile elle-même, avec son système de suspension, constitue un oscillateur muni d'amortisseurs efficaces qui évitent que le véhicule n'entre en résonance aiguë.
Le dessin des pneumatiques est parfois périodique. De ce fait le roulement produit un bourdonnement. Sur certains pneumatiques le dessin peut être légèrement déphasé pour atténuer ce phénomène.
[modifier | modifier le code]
Les vagues engendrent des mouvements oscillatoires des navires. Sur un navire libre, faute de raideur, les mouvements dans le plan horizontal (cavalement, embardée et lacet) ne peuvent être soumis à la résonance. Restent le roulis, le tangage et le pilonnement, ces deux derniers étant généralement assez amortis pour ne pas être critiques. Malheureusement la période propre de roulis tombe en général dans les périodes de vagues, le mouvement étant par ailleurs assez peu amorti. La meilleure solution pour lutter contre ce phénomène consiste à éviter de prendre les vagues par le travers. Il est également possible d'augmenter l'amortissement en ajoutant à la coque des appendices nommés quilles de roulis.
Sur les navires amarrés au large apparaît un autre phénomène, plus subtil, la dérive lente. En général, le système navire-amarrage a une période propre qui s'exprime en minutes. Elle ne peut donc être excitée par les vagues qui contiennent des périodes allant de quelques secondes à quelques dizaines de secondes mais l'excitation provient de termes non linéaires. Ceux-ci créent de nouvelles fréquences sommes et différences de celles que contiennent les vagues, conformément à la formule de trigonométrie sur le produit de cosinus. Les forces correspondantes sont très petites mais, l'amortissement étant lui-même très faible, la résonance induit des mouvements qui peuvent déplacer d'une ou deux dizaines de mètres un navire de quelques centaines de milliers de tonnes.
Génie civil[modifier | modifier le code]
Ponts[modifier | modifier le code]
Un pont peut effectuer des oscillations verticales, transversales ou de torsion. À chacun de ces types d'oscillations correspond une période propre ; si le tablier est suspendu (maintenu par des câbles accrochés aux piliers), le système a une fréquence de résonance bien différente.
Le 16 avril 1850, une troupe traversant en ordre serré le pont de la Basse-Chaîne, pont suspendu sur la Maine à Angers, provoqua la rupture du pont par résonance et la mort de 226 soldats[5]. Pourtant, le règlement militaire interdisait déjà de marcher au pas sur un pont, ce qui laisse à penser que ce phénomène était connu auparavant. Un accident similaire quoique moins grave avait eu lieu en Angleterre le 12 avril 1831 sur le pont de Broughton[5].
Le 7 novembre 1940, de forts vents (de 65 à 80 km/h) provoquèrent la chute du pont du détroit de Tacoma (États-Unis) Vidéo. Des vibrations de flexion transversale amenèrent la rupture d'un câble, puis du reste de l'œuvre. La première explication fournie s'appuyait sur l'excitation d'une résonance par le détachement périodique de tourbillons dans une allée de Karman. En fait, la fréquence observée des vibrations était très inférieure à la fréquence de détachement qu'il est possible de calculer. Il sembla donc qu'il fallut abandonner, dans ce cas, l'explication par une résonance pour la remplacer par celle qui fait appel à la notion d'instabilité aéroélastique. Dans un système linéaire possédant au moins une fréquence propre, comme ceux qui ont été envisagés précédemment, la stabilité est assurée quand le système est dissipatif, ou à la limite conservatif. Ici, le système devient actif : dans un vent que l'on peut supposer constant, à mesure que le tablier se tord, le moment des efforts aéroélastiques peut être approché par sa composante en phase avec le déplacement (pseudo-raideur) et sa composante en quadrature, proportionnelle à la vitesse de vibration. Dans le couplage d'une structure avec un fluide léger, les efforts aéroélastiques sont négligeables devant les forces d'inertie ou les efforts élastiques de la structure, sauf au voisinage des fréquences car ceux-ci s'y compensent. La composante en quadrature, quand elle s'oppose à l'amortissement, traduit l'apport d'énergie éolienne à la structure, cause de l'instabilité aéroélastique. Le mode de torsion devient instable, ce qui correspond à des oscillations d'amplitude croissante. La rupture peut alors survenir. L'instabilité se produit toujours au voisinage d'un mode propre et donc d'une fréquence propre dans le couplage fluide léger-structure, cas des problèmes d'aéroélasticité que l'on rencontre aussi sur les avions, sur les moteurs d'avion... Le pont fut reconstruit en tenant compte de ce problème et est toujours en place[6].
Le pont du Millenium a été construit à Londres pour l'an 2000. Il dut être modifié à la suite d'un problème d'instabilité latérale engendré par le couplage de la marche des piétons avec le premier mode latéral.
Un phénomène analogue fut rencontré à Paris à la même époque avec la passerelle Léopold-Sédar-Senghor.
Chemins de fer[modifier | modifier le code]
La construction ferroviaire rencontre aussi des problèmes liés à la résonance. Les fils suspendus aux caténaires constituent des oscillateurs liés entre eux. Afin d'éviter qu'ils se transmettent l'onde due au contact avec les trains, les caténaires ne sont pas disposés à égales distances. Il en est de même pour les rails posés sur les traverses, mais le phénomène est observable pour des fréquences plus élevées.
Bâtiments[modifier | modifier le code]
Les bâtiments sont sensibles aux tremblements de terre. Certains dispositifs passifs permettent de les protéger : il s'agit d'oscillateurs (gros pendule suspendu en haut de l'immeuble) dont la fréquence propre est voisine de celle du bâtiment lui-même. Ainsi l'énergie est absorbée par le pendule empêchant l'immeuble de se briser.
Résonances marines[modifier | modifier le code]
Les ports sont le lieu d'ondes stationnaires de périodes bien définies appelées seiches. Dans certains sites, ces ondes peuvent être excitées par les trains de vagues, créant ainsi des oscillations horizontales qui peuvent être dommageables pour les bateaux amarrés.
Un phénomène similaire est également régulièrement observé sur les récifs coralliens : les ondes longues libérées par les groupes de vagues courtes lors de leur déferlement peuvent être piégées sur le lagon corallien en raison du fort gradient bathymétrique entre l'océan et la barrière de corail : les ondes longues atteignent la plage, sont réfléchies vers l'océan et sont de nouveau réfléchies dans la direction de la plage quand la fin du récif est atteint, en raison du changement brusque de bathymétrie, ce qui génère un phénomène de résonance.
Comme dans les ports, de tels phénomènes de résonance sont seulement significatifs pendant les tempêtes : en effet, la quantité d'énergie présente dans les ondes longues (communément appelées ondes infragravitaires) augmente très significativement lors des périodes énergétiques, en raison des transferts d'énergie allant des vagues courtes vers les ondes longues.
Un phénomène analogue, à plus grande échelle, s'observe dans les golfes, l'excitation étant fournie par les ondes de marée. Il ne présente pas d'inconvénients particuliers et peut même être utilisé par des usines marémotrices.
Enfin, les tsunamis (et météotsunamis) sont aussi amplifiés par résonance dans les baies et golfes (l'emprise spatiale de ce phénomène est très variable et dépend de la période du tsunami), ce qui peut amener à des submersions marines catastrophiques. A la différence de la résonance observée pour les ondes de marée, les tsunamis ne sont influencés que de manière négligeable par la force de Coriolis, qui dévie l'onde vers la droite dans l'hémisphère nord (et vers la gauche dans l'hémisphère sud).
Résonances en aéronautique[modifier | modifier le code]
Un hélicoptère peut, lorsqu'il est posé, produire un phénomène de résonance en rapport avec la rotation du rotor principal, il est souvent conseillé aux pilotes de décoller lorsque ce phénomène se manifeste pour éviter la dislocation de l'appareil.
Dans la propulsion des fusées à ergols liquides, il peut aussi se produire un phénomène oscillatoire longitudinal, provoqué par des fluctuations de poussée du moteur, qui engendrent des vibrations de structure et des colonnes du carburant liquide, qui à leur tour se répercutent sur l'alimentation du moteur. Lorsque ce cycle de perturbations entre en résonance, les oscillations augmentent et peuvent détruire les structures. On appelle ce type de résonance l'effet pogo.
Évolution historico-épistémologique du concept de résonance[modifier | modifier le code]
Introduction : aspects scientifiques, techniques, et sociaux[modifier | modifier le code]
Le contexte scientifique, dans lequel le concept de résonance s'est développé est riche, de par la multiplicité des phénomènes physiques qu'il a été appelé à expliquer. En effet, tout type d'onde est concerné, qu'il soit par exemple mécanique, acoustique, ou électromagnétique. De plus, les systèmes oscillants occupent une large échelle de dimensions (en termes de distance) : de la particule élémentaire (tel l'électron) ou atomique jusqu'au système planétaire.
En termes d'ingénierie, l'implication du phénomène de résonance est tantôt recherchée, tantôt évitée. Différents détecteurs et transducteurs (utilisation métrologique) exploitent effectivement des systèmes physiques résonnants (les filtres électroniques, les capteurs de pression ou d'accélération à quartz piézoélectrique, et le réfractomètre à résonateur optique, par exemple), afin d'amplifier les signaux mesurés. Au contraire, la résonance d'une structure mécanique, soumise à une contrainte oscillante, peut conduire à sa rupture; l'amplitude de ces oscillations doit donc être amortie. Ainsi, l'aspect technique du phénomène de résonance peut apparaître naturellement (de lui-même), ou au contraire, être généré artificiellement.
Par ailleurs, la création et l'évolution (socio-historique) d'un concept scientifique, se heurte à différents obstacles épistémologiques, au sens de Gaston Bachelard[7]: "[…] c'est en termes d'obstacles qu'il faut poser le problème de la connaissance scientifique. [...] C'est dans l'acte même de connaître […] que nous décèlerons des causes d'inertie que nous appellerons des obstacles épistémologiques". La communauté de mathématiciens et physiciens ayant travaillé sur le phénomène de résonance a effectivement rencontré de telles difficultés. Cependant, une rupture épistémologique aura progressivement conduit à un travail d'abstraction, puis de conceptualisation, réunissant ainsi une variété d'expériences et d'observations en un seul phénomène physique, au contenu théorique général.
Construction du concept théorique de résonance (histoire)[8][modifier | modifier le code]
De la préhistoire au XXe siècle : du son à la musique[modifier | modifier le code]
Le phénomène de résonance pouvait être constaté par l'homme préhistorique, notamment du fait de la résonance acoustique dans les grottes. De plus, les premiers instruments permettant la création, le prolongement et l'amplification du son remontent à l'ère du Paléolithique. En effet, les plus anciens instruments de musique connus datent de 100 000 ans avant notre ère.
À cette époque la résonance n'était pas encore identifiée comme un concept, ni même un phénomène. Néanmoins, l'appréhension pragmatique (par l'ouïe) des effets sonores de la résonance conduit au développement d'un domaine artistique : celui de la musique. Plusieurs siècles de recherche scientifique et de formalisation des connaissances seront nécessaires pour reconnaitre que le phénomène de résonance sonore est fondamental pour la création et l'amplification du son de tout instrument de musique. Si cette résonance est généralement de type acoustique (la voix, la flûte, l'orgue, le violon), certains instruments de musique contemporains exploitent une résonance électronique (le synthétiseur, la guitare électrique).
Les premiers instruments à cordes, munis desdites caisses de résonance, sont apparus au cours du premier tiers de l'Antiquité (environ 2 500 ans av. J.-C.). Motivés par un désir de précision et de qualité sonore, les constructeurs d'instruments et musiciens modifieront et diversifieront leurs créations, tant en forme qu'en structure. Bien que ces artisans ne comprenaient pas nécessairement le phénomène de résonance acoustique, celui-ci était toujours présent, et à l'origine des différentes sonorités des instruments de musique. Par ailleurs, la résonance acoustique dominera (exclusivement) l'univers musical, jusqu'en 1948, c'est alors que les récents développements de l'électronique analogique permirent à Clarence Leo Fender[9] (1909-1991), ainsi qu'à George William Fullerton (1923-2009) de concevoir la première guitare électrique commercialisée en masse.
Antiquité grecque : phénoménologie acoustique, premier modèle cosmologique[modifier | modifier le code]
Au cours du Ve siècle av. J.-C. Pythagore construisit un instrument monocorde, afin de caractériser le son (les notes musicales), émis par la corde vibrante, lorsque celle-ci était divisée en des rapports entiers. Aidé par ces disciples, ce philosophe élaborera ainsi une gamme musicale, construite sur la quinte. Elle sera le fondement théorique de la musique (musicologie), durant les vingt prochains siècles[10].
Par ailleurs, plusieurs explications (philosophiques et scientifiques) dues à l'école Pythagoricienne étaient précisément basés sur des rapports géométriques. Ces derniers sont, par exemple, à l'origine des mathématiques de l'Antiquité. En particulier, Pythagore percevait les nombres entiers comme étant à l'origine de tout principe fondamental, traduisant notamment l'harmonie.
En conséquence, le modèle cosmologique qu'il créa, était basé sur la gamme pythagoricienne. Ce modèle géocentrique, nommé « Musica Universalis », ou « harmonie des sphères », disposait effectivement les astres connus à cette époque (Soleil, Lune, quelques planètes) sur des orbites circulaires, dont la longueur des rayons suit les rapports musicaux (harmonieux). Cette explication métaphysique de la géométrie de l'univers (plus spécifiquement, du système solaire), bien que fondée sur la résonance sonore d'une corde, inspira les astronomes jusqu'au XVIe siècle.
C'est alors que les bases de la musicologie furent posées, que Platon (environ 428 - 348 av. J.-C.) et Aristote (environ 384 - 322 av. J.-C.) étaient à même de discuter le phénomène d'influence d'un son émis par une corde sur une autre, ainsi que celui de résonance multiple. Ces deux philosophes observèrent la relation étroite, voire "l'affinité", "la sympathie", pouvant exister entre deux (éventuellement plusieurs) notes musicales. Néanmoins, à une époque où la physique des ondes n'existait pas, ils furent incapables d'en proposer quelconque explication, reposant sur une description théorique ainsi que sur des principes physiques fondamentaux.
Du XVIe au XIXe siècle : différentes théories physiques : astronomie, acoustique, mécanique, électromagnétisme[modifier | modifier le code]
Les marées et la résonance des bassins océaniques (du XVIe au XIXe siècle)[modifier | modifier le code]
Bien que Platon, au cours de l'Antiquité, identifia l'origine du phénomène de "marée" au mouvement périodique des masses d'eau océaniques, il faudra attendre le début du XVIIe siècle, afin que la description théorique de ce phénomène se précise.
À cette époque, Kepler (1571-1630), puis Descartes (1596 - 1659) expliquaient la marée par la force gravitationnelle, exercée par la Lune sur la Terre. Une explication des marées, contemporaine de celle des deux scientifiques précédents, est due à Galilée (1564-1642). Défenseur du modèle héliocentrique, il rendait compte de ce phénomène par les deux mouvements de rotation de la Terre (sur elle-même, ainsi qu'autour du Soleil). Cette théorie, qui s'oppose aux idées de Kepler et Descartes, s'avéra fausse[11]. Néanmoins, elle inspira le mathématicien anglais Wallis (1642-1727), qui utilisa les arguments de Galilée (force centrifuge), afin de rendre compte de la nature cyclique des marées.
À la suite du développement de sa théorie universelle de la gravitation (1687), Newton (1642-1727) expliqua que les deux seuls astres suffisamment massifs, respectivement, suffisamment proches de la Terre, pour y influencer le phénomène de "marée", sont le Soleil et la Lune.
Le mathématicien français Pierre-Simon Laplace (1749-1827) enrichira les idées de Newton, concernant les marées, en les modélisant par des ondes mécaniques se propageant à la surface des océans. Cette perturbation est une réponse à l'excitation gravitationnelle du Soleil et de la Lune. Les marées sont alors assimilées à des vagues de très longue longueur d'onde.
Afin de rendre compte des particularités locales des marées (périodicité et amplitude différentes, voire variables, en fonction des côtes), l'américain Rollin A. Harris (1863-1918) introduisit le phénomène de résonance des bassins océaniques (1897). Sa théorie explique comment les différentes géométries des bassins océaniques peuvent amener les ondes de marée à être amplifiées ou atténuées, de manière à changer leur période et leur hauteur. Le frottement des masses d'eau sur la croûte terrestre empêche une augmentation démesurée de cette amplitude, dans le cas où une telle résonance a lieu[12].
Résonance orbitale (début du XIXe siècle)[modifier | modifier le code]
Dès lors que la théorie universelle de la gravitation fut formulée par Newton, les astronomes s'interrogeront sur le célèbre problème à trois corps, ainsi que sur celui de la stabilité de orbites (planétaires, notamment). La nature stable, ou au contraire instable, de certaines orbites sera mise en évidence par Laplace, alors qu'il introduira la notion de "résonance orbitale", dans le système solaire. Le premier quart du XIXe siècle connut ainsi l'introduction du phénomène de résonance en astrophysique.
Par définition, une telle résonance a lieu, lorsque le rapport des périodes de deux corps orbitant autour d'un troisième est une fraction rationnelle. Dans ce cas, l'attraction gravitationnelle d'un corps sur l'autre exhibe une excitation périodique. Celle-ci conduit généralement à l'augmentation rapide et importante de l'amplitude du mouvement orbital, d'où une éjection d'un corps (ou des deux) de son orbite. Néanmoins, dans certains cas, ladite excitation périodique, d'un corps massif sur un autre, moins massif, peut contrebalancer certaines perturbations gravitationnelles, restabilisant ainsi l'orbite de ce dernier, de manière régulière (résonance orbitale de la planète naine Pluton, avec Neptune, par exemple).
Résonance acoustique (XVIIe et XVIIIe siècles)[modifier | modifier le code]
La science acoustique connut d'importantes avancées, au XVIIe siècle. En ce temps, les aspects physiques et musicaux étaient étudiés en parallèle. L'analyse des sons harmoniques constituait alors le lien entre ces deux théories.
En procédant à des expériences sur des cordes vibrantes et le phénomène d'influence des sons, Galilée est amené à des considérations d'ordre physiologique. Il associe la consonance des notes musicales à des percussions simultanées sur le tympan.
Cette excitation de sons consonants par une note donnée sera également relevée dans le Compendium Musicae[13], rédigé par René Descartes (1596-1650), en 1618. Cet ouvrage marqua l'histoire de la théorie musicale.
Par ailleurs, les travaux expérimentaux (sur divers objets sonores) menés par Marin Mersenne (1588-1648), l'amèneront à définir la notion de « sons harmoniques », comme étant la suite de sons préférentiellement excités par un ton fondamental.
Pour l'essentiel, le XVIIe siècle identifie donc la résonance à l'excitation d'une corde non frappée, par une corde vibrante. Les expériences et observations réalisées sur des corps sonores plus sophistiqués, tels que des cloches et des tuyaux, conduiront le terme de résonance à caractériser l'accompagnement naturel des consonances harmoniques, associé à un corps vibrant (ton fondamental).
En 1753, Daniel Bernoulli (1700-1782) travailla sur l'unification des théories physiques à l'origine de la propagation du son et de la vibration d'une corde. Il utilisa les développements mathématiques de Jean le Rond d'Alembert (1717-1783) et Leonhard Euler (1707-1783), proposés dès 1747. En effet, l'unification en question s'inscrivait à l'intersection entre les travaux de ces trois scientifiques, dont les contributions à l'hydrodynamique et à la physique des ondes furent décisives.
Résonateur de Helmholtz (XIXe siècle)[modifier | modifier le code]
Le physicien et physiologiste Hermann von Helmholtz (1821-1894) consacra plusieurs années de sa vie à l'étude de la perception des sens humains (la vue et l'ouïe, notamment). Vers 1860, il fournit une explication physique de l'audition, dans laquelle le son perçu est amplifié par résonance, dans l'oreille[14].
Ses travaux en acoustique le menèrent à la construction d'un dispositif portant aujourd'hui son nom: "le résonateur de Helmholtz". Celui-ci consiste en une cavité acoustique résonante, permettant d'"isoler" un ton fondamental, issu d'un son complexe (composé de multiples tons et de leurs harmoniques), en l'amplifiant. Parallèlement, les autres fréquences sonores sont atténuées[14]. De par son mode de fonctionnement, ainsi que son aspect musical, cet objet représente le précurseur de tout diapason.
Le premier modèle expérimental d'un tel résonateur fut construit à partir d'une bouteille de vin, dont Helmholtz remplaça successivement le fond par des membranes de différentes épaisseurs et souplesses, de manière à identifier leur « fréquence propre ». Par la suite, ces résonateurs prendront la forme de cylindres ou de sphères métalliques, dont la fréquence propre est précisément caractérisée par leurs dimensions[14].
Cette résonance sonore, à nouveau, dite « de Helmoltz », met en évidence certains tons plutôt que d'autre. En conséquence, elle est utilisée en acoustique des salles, de manière qu'un auditoire soit adapté aux représentations qu'il est censé accueillir (théâtre, concerts)[14].
Dans sa publication (pionnière) de 1863, On the Sensations of Tone as a Physiological Basis for the Theory of Music, Helmholtz abordera conjointement les aspects physiques, physiologiques et musicaux des tons sonores[14].
Le phénomène de résonance connaît à cette époque une révolution conceptuelle. En effet, l'explication des phénomènes vibratoires invoque désormais les notions d'"excitateur", de « résonateur » et de « fréquence propre ». Néanmoins, cette nouvelle perspective ne se fera pas remarquer avant 1877, dans les travaux de Helmholtz, alors qu'il écrivait « phénomène de communication des vibrations », afin de désigner la « résonance »[15]. Enfin, pour décrire les aspects énergétiques de ses résonateurs (accumulation d'énergie), il exploita une analogie avec la résonance mécanique, grâce à laquelle un homme (excitateur) peut mettre en oscillation une lourde cloche (résonateur).
Résonance électromagnétique (fin du XIXe siècle)[modifier | modifier le code]
En 1887, les travaux de Heinrich Hertz (1857-1894) sur les ondes électromagnétiques l'amenèrent à concevoir un résonateur permettant de transférer l'énergie d'un circuit électrique à un autre, sans qu'aucun conducteur ne les lie.
L'expérience qu'il réalisa, et qui porte aujourd'hui son nom, mit en œuvre un émetteur (excitateur) et un récepteur (résonateur). L'émetteur était constitué d'une bobine de Rhumkorff (une forme de transformateur) permettant de générer un arc électrique entre deux sphères chargées (haute tension). Le récepteur se résumait à un anneau métallique ouvert, dont les deux extrémité étaient proches l'une de l'autre. La brève impulsion du champ magnétique (transférée sous la forme d'ondes électromagnétiques), à l'intérieur de cet anneau, crée (par induction magnétique) une tension aux bornes de celui-ci, laquelle est visualisée par une étincelle, entre les deux extrémités de l'anneau[16].
Hertz fut ainsi capable de vérifier la théorie de l'électromagnétisme, présentée par Maxwell, ainsi que d'identifier la lumière comme une onde électromagnétique, en étudiant les propriétés (polarisation, réflexion, etc.) des ondes radio qu'il avait créée[16].
Au même moment, en France, le professeur de physique Edouard Branly (1844-1940) mena des travaux similaire. Contrairement à Hertz, le chercheur français envisageait l'utilisation de ce phénomène physique nouvellement découvert, à des fins de communication[17].
Ainsi, ces expériences fondatrices permirent le développement des circuits électroniques résonnants. Elles inspirèrent notamment Guglielmo Marconi (1874-1937), inventeur de la radiotélégraphie, qui marqua le début d'une nouvelle ère de la télécommunication[18]. De même, elles motivèrent les travaux de nombreux inventeurs, tel que le célèbre Nikola Tesla (1856-1943), qui adressaient les siens (réseau de distribution d'énergie, radio, radar) au profit de l'humanité[17].
Matière et rayonnement (XXe siècle)[modifier | modifier le code]
Au début du XXe siècle, l'avènement de la physique quantique révolutionnait la perception que la science avait du monde microscopique. Son objectif initial était de remédier aux échecs auxquels les théories physiques dites "classiques" étaient confrontées, quant à l'explication de différentes observations (rayonnement du corps noir, expérience de Franck et Hertz, effet Compton, etc.).
L'analogie entre "particules de matière" et "onde" amena précisément la résonance à expliquer certains phénomènes, au cœur des interactions entre "matière" et "rayonnement". Ceux-ci sont le fondement des techniques modernes de spectroscopie, ainsi que des résonateurs optiques (à la base des lasers). Ces derniers sont notamment utilisés dans l'infrastructure matérielle nécessaire à la communication optique (internet, téléphonie).
D'autre part, la quantification de l'absorption et de l'émission d'énergie par les électrons atomiques rend compte du spectre de raie, propre à chaque élément. Robert Bunsen (1811-1899) et Gustav Kirchhoff (1824-1887) étudièrent de tels spectres à partir de 1859, puis ils s'en servirent pour caractériser différents éléments chimiques (prototype du spectroscope). Ces deux scientifiques sont ainsi les pères de l'analyse des spectres, mais ils ne fournirent pas d'explication, concernant leur origine physique.
La quantification des ondes électromagnétiques fut proposée en 1900 par Max Planck (1858-1947), à la suite de ses analyses du rayonnement de corps noir (problématique de ladite "catastrophe ultraviolette"). Sur la base de ces travaux, Albert Einstein (1879-1955) développa sa théorie de l'effet photo-électrique (1905), pour laquelle il reçut le prix Nobel de Physique de 1921[19].
En 1911, Ernest Rutherford (1871-1937), père de la physique nucléaire, proposa un modèle atomique planétaire, afin de rendre compte de la structure matérielle de l'atome, qu'il avait observé sur des feuilles d'or (interaction des électrons avec les atomes du métal). Deux ans plus tard (1912), Niels Bohr (1885-1962) se servira du premier postulat quantique proposé par Planck, afin de réviser le modèle de Rutherford, en y imposant la quantification du moment cinétique (orbital) des électrons. Cette hypothèse conduit elle-même à la quantification des orbites électroniques stables, laquelle est à l'origine des spectres de raies, via l'absorption ou l'émission quantifiée d'énergie (par l'électron).
Louis De Broglie (1892-1987) propose en 1923, ses considérations, selon lesquelles des propriétés ondulatoires peuvent être attribuées aux particules (dualité "onde - particule"). Il assimile les orbites électroniques à des ondes stationnaires, comparables à celles des modes résonnants d'une corde vibrante. Ces considérations rendent compte de la stabilisation desdites orbites, et corroborent la quantification de leur énergie, imposée par Bohr, dix ans plus tôt. Dans ce modèle, l'électron est alors perçu comme un oscillateur (dipôle électrique), pouvant être stimulé (oscillations forcées) par un champ électrique oscillant (ondes électromagnétiques). Les transferts d'énergies s'effectuent alors pour des fréquences bien déterminées, propres à l'atome en question. En particulier, Werner Heisenberg (1901-1976) emploiera le terme résonance[20] en 1926, alors qu'il travaillait sur les oscillateurs quantiques couplés.
Épistémologie du phénomène de résonance[modifier | modifier le code]
Les différentes conceptions de la résonance[modifier | modifier le code]
Au cours de son évolution historique, la résonance[8] a connu trois conceptions principales.
Jusqu'à la fin du XVIe siècle, la résonance était associée à la production, au prolongement et à l'amplification du son. De plus, elle était alors perçue comme l'attribut d'un unique corps sonore. Elle ne sous-entendait pas une interaction entre deux objets, ou entre une onde et un objet.
Par la suite, la résonance désigna la production d'harmoniques par un objet sonore, excité par un son d'une source extérieure, de fréquence dite fondamentale. Néanmoins, ce phénomène était essentiellement connu sous le terme de "communication des vibrations", jusqu'à la fin du XIXe siècle.
Enfin, la résonance acquit son sens le plus récent, qui est également le plus général. Elle caractérise à présent le couplage "excitateur-résonateur", impliquant notamment un transfert d'énergie. Tout type d'onde est concerné, ce qui permet un nombre important d'applications, métrologiques (capteurs, notamment).
Ainsi, la conceptualisation du phénomène de résonance a été mue par un mécanisme d'abstraction. Initialement attribué à des objets perceptibles (essentiellement sonores), il a progressivement été intégré dans le comportement d'objets (vibrant, oscillant) et/ou ondes (divers types) en interaction.
Obstacles épistémologiques[modifier | modifier le code]
L'évolution du concept théorique de résonance a essentiellement connu trois obstacles épistémologiques.
Le premier obstacle est terminologique et provient de l'étymologie du mot résonance, évoquant le son. Cette conception de la résonance, associée au prolongement du son ainsi qu'à la transmission des vibrations, trouve son origine au XVe siècle et nuira à une nouvelle conceptualisation et généralisation du phénomène de résonance, jusqu'à la fin du XIXe siècle. À cette époque, l'introduction de l'interaction entre un excitateur et un résonateur permet alors de généraliser le phénomène à tout type d'ondes. Cette association de la résonance aux phénomènes ondulatoires mènera ainsi à une description théorique, générale, du phénomène physique. L'obstacle terminologique, ou "verbal", susmentionné est donc issu du caractère polysémique de certains termes scientifiques.
Le second obstacle, dit "substantialiste", est lié à la conception initiale de la résonance comme l'attribut d'un objet émetteur de son, et non comme un phénomène physique d'excitation. Le détachement du phénomène de résonance de tout contenu matériel aura finalement permis sa généralisation à divers domaines de la physique.
Le troisième obstacle est conceptuel. Il correspond à la difficulté de traduire des observations particulières, réelles et matérielles en un phénomène conceptuel et abstrait. À la fin du XIXe siècle, cette conceptualisation du phénomène de résonance associera néanmoins la résonance à divers types d'ondes, ainsi qu'à des objets en mouvement oscillatoire de toute dimension. La qualification faite du phénomène de "transmission des vibrations" par le terme résonance en est un exemple.
Conclusion : interactions science-société et société-science[modifier | modifier le code]

De par la diversité des phénomènes physiques étudiés au cours des siècles, la notion de résonance, à connotation initialement naturelle, perceptive et sonore a pu être généralisée à tout système physique oscillant.
De plus, l'évolution conceptuelle du phénomène théorique de résonance, conjointement avec la terminologie initialement pragmatique, et n'ayant pas été ré-adaptée, a conféré au terme résonance le caractère polysémique qu'on lui connaît aujourd'hui, en sciences et en techniques (voir la figure sur l'évolution diachronique de la résonance[21]). (Celui-ci contraste avec le sens essentiellement "sonore" qui lui est encore associé, dans un contexte non-scientifique.)
Par ailleurs, l'omniprésence du phénomène de résonance s'est historiquement traduite par une grande diversité de la communauté de chercheurs qui a contribué à sa formalisation. Leur motivations étaient donc très variées: philosophique, physiologique (médical), physique, et musicale.
Enfin, la résonance, à l'appui de plusieurs théories physiques a également conduit au développement de différentes technologies, dans les domaines de l'ingénierie (mécanique, électrique, télécommunications, etc.), de la métrologie (recherche fondamentale), et de l'imagerie biomédicale, par exemple.
Notes et références[modifier | modifier le code]
- (en) F. Bloch, W.W. Hansen et M. Packard, « The Nuclear Induction Experiment », Phys. Rev., vol. 70, , p. 474–485 (DOI 10.1103/PhysRev.70.474)
- (en) F. Bloch, « Nuclear Induction », Phys. Rev., vol. 70-pages=460–474, (DOI 10.1103/PhysRev.70.460)
- (en) E.M. Purcell, H.C. Torrey et R.V. Pound, « Resonance Absorption by Nuclear Magnetic Moments in a Solid », Phys. Rev., vol. 69, , p. 37–38 (DOI 10.1103/PhysRev.69.37)
- (en) R. Damadian, « Tumor Detection by Nuclear Magnetic Resonance », Science, vol. 19, , p. 1151-1153 (DOI 10.1126/science.171.3976.1151)
- Hervé Lehning, Toutes les mathématiques du monde, Paris, Flammarion, , 447 p. (ISBN 978-2-08-135445-6), partie 4, chap. 32 (« Les mathématiques architecturales »), p. 334.
- (en) http://www.vibrationdata.com/Tacoma.htm
- Gaston Bachelard, La formation de l'esprit scientifique, Paris, Vrin, , p. 14
- Ali Mouhouche et El-Hajjami Abdelkrim, « Étude de la résonance: quels obstacles épistémologiques », Le Bup, no 204, , p. 599-613
- (en) « leo Fender », sur Encyclopaedia Britannica (consulté le )
- Paul Chartier, Maxime Jullien, Clément Le Roy, « Gamme pythagoricienne », sur TPE: Le passage de la musique modale à la musique tonale (consulté le )
- Richard Taillet, « Théorie des marées de Galilée : une simulation », sur Signal sur bruit (consulté le )
- INP, ENSEEIHT, « Les Marées: Pourquoi? Comment? », sur Un peu d'Histoire... (consulté le )
- André Charrak, Raison et perception. Fonder l'harmonie au XVIIIe siècle, Paris, Vrin, , p. 26
- (en) Lydia Patton, « Hermann von Helmholtz », sur The Stanford Encyclopedia of Philosophy, (consulté le )
- Hermann von Helmholtz, Causes physiologiques de l'harmonie musicale, Paris, G. Baillère, , p. 181
- Pierre Dessapt, « L'électromagnétisme et la propagation des ondes », sur RACONTE MOI LA RADIO (consulté le )
- (en) Jed Z. Buchwald et Robert Fox, The Oxford Handbook of the History of Physics, OUP Oxford,
- « Guglielmo Marconi », sur LAROUSSE (Encyclopédie) (consulté le )
- Manjit Kumar, Le grand roman de la physique quantique : Einstein, Bohr... et le débat sur la nature de la réalité, Jean-Claude Lattès,
- Encyclopedia Universalis, vol. 14, France S. A., , p. 136
- Ali Mouhouche et El-Hajjami Abdelkrim, « Étude diachronique et évolution du concept de résonance en physique », Meta, no 582, , p. 430-448
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Jacques Jouhaneau, Notions élémentaires d’acoustique, 2e éd., 5.1 et 5.2, CNAM, TEC&DOC, 2000 (ISBN 2743003073)