Catastrophe ultraviolette

Cet article a besoin d’être illustré (en discuter). Pour améliorer cet article, des médias (images, vidéos, sons) sous licence libre ou du domaine public sont les bienvenus. Si vous êtes l’auteur d’une image que vous souhaitez partager, importez-la. Si vous n’êtes pas l’auteur, vous pouvez néanmoins faire une demande de libération d’image à son auteur.

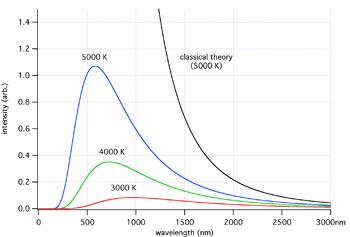
La catastrophe ultraviolette est l'erreur mise en évidence pour les courtes longueur d'ondes (correspondant à T > 5000K) dans la loi de Rayleigh du modèle classique (courbe en noir), donnant l'énergie émise par un corps noir idéal (la courbe correcte est celle en bleue prédite par la loi de Planck).

La catastrophe ultraviolette, c'est un terme employé pour la première fois par le physicien autrichien Paul Ehrenfest. Elle désigne les résultats de plusieurs expériences faites au cours de l'année 1900, résultats qui se sont avérés non concordants avec la théorie élaborée entre les années 1880 et 1900 pour expliquer le rayonnent émis par un corps chauffé (en chauffant du métal, il devient rouge, en le chauffant encore plus, il devient blanc).

Cette théorie du rayonnement prévoit que le rayonnement émis par un corps chauffé est proportionnel à la température absolue et inversement proportionnel au carré de la longueur d'onde.

Au cours de l'année 1900, des expériences montrent que cette théorie du rayonnement fonctionne bien pour des émissions allant de l'infra-rouge au vert. Par contre, pour le bleu, le violet, et plus encore, l'ultraviolet, les résultats ne concordent pas du tout avec cette théorie qui est mise en échec.

C'est pour apporter une réponse à ce problème de théorie du rayonnement que le physicien allemand Max Planck propose à la fin de l'année 1900 une idée révolutionnaire qui, pour la première fois, postule qu'un phénomène physique peut être discontinu. C'est la naissance de la physique quantique qui va bientôt supplanter la physique classique.

Résolution classique du corps noir

Un corps noir est modélisé par une cavité contenant de l'énergie sous forme d'un champ électromagnétique. En raison des conditions aux limites, le champ prend la forme d'une onde stationnaire admettant un ensemble discret de modes. Par exemple, les modes horizontaux d'une boîte ne peuvent avoir pour fréquence que

$\,\nu = nc/L$

où L est la longueur de la boîte, n un entier naturel non nul quelconque et c la vitesse de la lumière.

Ci-dessous: illustration des conditions aux limites en dimensions 1 et image des modes propres discrets possibles (voir aussi les articles Corde vibrante et Onde stationnaire)

En électromagnétisme, on montre plus généralement que le nombre de modes par unité de fréquence de la cavité est proportionnelle au carré de la fréquence :

$\,\frac{\mathrm{d}N}{\mathrm{d}\nu} \propto \nu^2$.

En appliquant le théorème d'équipartition de l'énergie, chaque mode doit contenir une énergie kT/2, où k est la constante de Boltzmann et T la température du système. Il en résulte que l'énergie par unité de fréquence suit la loi de Rayleigh-Jeans :

$\frac{\mathrm{d}E}{\mathrm{d}\nu} \propto T\nu^2$.

Ainsi l'énergie par unité de fréquence tend vers l'infini lorsque la fréquence tend vers l'infini et l'énergie totale est infinie.

Résolution quantique du corps noir

TBW.

Articles connexes

• Histoire de la mécanique quantique
• autres mises en défaut de la physique classique
  • effet photo-électrique
  • raie spectrale
  • dualité onde-particule de la lumière
• domaines de la physique concernés
  • électromagnétisme
  • thermodynamique et physique statistique
  • physique quantique
• auteurs
  • Paul Ehrenfest
  • Max Planck
• autres
  • divergence ultraviolette

Bibliographie

• Claude Cohen-Tannoudji, Bernard Diu, Franck Laloë, Mécanique quantique : Tome 1, Hermann, Paris (1977)