Paradoxe des jumeaux
En physique, le paradoxe des jumeaux ou paradoxe des horloges (Clock paradox) est un paradoxe issu d'une expérience de pensée qui semblait montrer que la relativité restreinte était contradictoire.
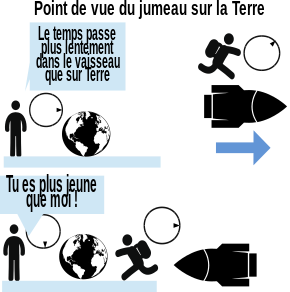
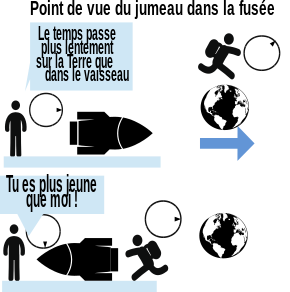
Des jumeaux sont nés sur Terre. L'un fait un voyage aller-retour dans l'espace en fusée à une vitesse proche de celle de la lumière. D'après le phénomène de dilatation des durées de la relativité restreinte, pour celui qui est resté sur Terre la durée du voyage est plus grande que pour celui qui est parti dans l'espace. Pour chaque jumeau, le temps s'écoule normalement à sa propre horloge, et aucune expérience locale ne permet au jumeau voyageur de déterminer qu'il est en mouvement pendant l'aller ou le retour. Mais quand ce dernier rejoint le jumeau terrestre, il s'aperçoit qu'il a mesuré au total moins de secondes et il rentre donc plus jeune que son jumeau sur Terre.
Toutefois, celui qui voyage est en droit de considérer, les lois de la physique restant identiques par changement de référentiel, qu'il est immobile et que c'est son frère et la Terre qui s'éloignent à grande vitesse de lui. Il pourrait donc conclure que c'est son frère, resté sur Terre, qui est plus jeune à la fin du voyage. Ainsi chaque jumeau pense, selon les lois de la relativité restreinte, retrouver l'autre plus jeune que lui. Est-on tombé sur un véritable paradoxe qui, comme Painlevé l'a indiqué à Einstein en 1922 (soit 6 ans après la publication de la relativité générale), peut mettre en cause la cohérence interne de la théorie de la relativité ?
La conclusion, admise dès les années 1930 par l'écrasante majorité des spécialistes, dit que le jumeau voyageur finit plus jeune que celui resté sur Terre, et que cette différence peut être considérée comme due à la dissymétrie entre les jumeaux car le voyageur change de référentiel galiléen pour revenir, alors que l'autre n'en change pas.
Depuis, cette conclusion a été confirmée expérimentalement à de nombreuses reprises, entre autres dans la désintégration des muons atmosphériques (1963), dans l'expérience de Hafele-Keating (1971), ainsi que par sa nécessaire prise en compte dans le réglage des GPS (1977) [2].
Discussions du paradoxe[modifier | modifier le code]
Pour la plupart des commentateurs, le jumeau voyageur B avait effectivement moins vieilli que son frère sédentaire A.
Pour les autres, les jumeaux avaient conservé le même âge ou le problème était sans signification[3].
La controverse tournait autour du fait que, du point de vue de la relativité restreinte, les situations des jumeaux ne sont pas symétriques : A coïncide avec un seul repère galiléen (en général celui de la Terre, idéalisé comme inertiel, pour l'occasion) pendant toute la durée du voyage, tandis que B effectue un demi-tour et coïncide ainsi avec au moins deux repères galiléens successifs. Cette différence fait que la relativité restreinte s'applique différemment à l'un et à l'autre, notamment à cause de l'accélération permettant le retour de B, en provoquant un changement de repère galiléen. Si, pendant la partie du voyage à vitesse constante, B vieillit moins vite qu'A, il se pourrait qu'il vieillisse plus vite durant les phases d'accélération. On relève 54 points de vue sur le paradoxe, émis entre 1905 (Einstein) et 2001 (Hawking)[4]. À la suite de Marie-Antoinette Tonnelat, on peut classer les prises de position en trois catégories : (1) Les acceptants (AR), pour qui la Relativité restreinte permet de conclure que pour finir B est plus jeune qu'A ; (2) Les opposants (OR), pour qui la Relativité restreinte permet de conclure qu'A et B se retrouvent au même âge ; enfin les généralisateurs pour qui le paradoxe ne peut se résoudre qu'à la lumière de la Relativité générale.
On peut affiner la classification de Tonnelat en distinguant la classe OG de ceux pour qui la Relativité générale conduisait à des conclusions différentes de celles couramment acceptées, et la classe AG de ceux pour qui la Relativité générale confirmait, mais avec des arguments différents, que B retrouve A en étant plus jeune que lui.
La classe AR[modifier | modifier le code]
Il s'agit de l'interprétation classique du paradoxe, qui regroupe la très grande majorité des commentateurs et entre autres J. Terrel, H. Arzeliès, H.E. Ives[5]. Pour eux les deux jumeaux auront vieilli différemment (dans un sens ou dans l'autre) justement du fait de la dissymétrie de leurs référentiels : celui de A est galiléen, contrairement à celui de B. Ce serait également la position d'Einstein[6].
La classe OR[modifier | modifier le code]
Parmi eux, suivant Tonnelat, on trouve les « Relativistes purs », tels Herbert Dingle[7] et E.G. Cullwick[8]. Pour eux, écrit Tonnelat, « il ne peut y avoir une modification des temps propres dans un mouvement qui ne met en jeu aucune accélération spécifique si l'on convient - comme c'est le cas - de les négliger ». Václav Hlavatý[9], qui a des arguments différents, serait également classé dans OR car ce dernier, dit Tonnelat, « souligne que les concepts de « repos » et de « mouvement » qui alimentent le « paradoxe du voyageur » réintroduisent les absolus newtoniens au sein de la Relativité Restreinte. D'autre part, la dissymétrie que l'on souligne dans la situation physique des jumeaux, l'un sédentaire, l'autre itinérant, l'un lié à un système d'inertie, l'autre s'en affranchissant, est tout à fait subjective ».
La classe OG[modifier | modifier le code]
Pour eux, toujours selon Tonnelat, « il faut appliquer des principes plus généraux qui permettent de calculer le mouvement « libre » de B dans le système propre de A, et réciproquement ». V.A. Fock[10] fait les calculs en choisissant un champ de gravitation donnant lieu à une accélération constante, champ de la forme avec . Il obtient alors que B vieillit moins qu'A si les temps d'accélération sont suffisamment courts et que ce phénomène s'inverse pour les temps d'accélération plus longs.
Pour Jean Chazy et René Dugas[11],[12], dit Tonnelat, « les périodes d'accélération dont on devrait tenir compte permettraient de rétablir une égale longévité entre les deux voyageurs: B éprouverait un vieillissement brusque qui compenserait très exactement le rajeunissement du voyage uniforme ».
La classe AG[modifier | modifier le code]
Les représentants de cette classe (Born, Pauli, Tolman entre autres)[13] « ont vu, dans une généralisation du principe de relativité, la méthode nécessaire pour résoudre au moins un aspect du problème (calcul des vieillissements dans le système propre de B) ».
Histoire[modifier | modifier le code]
Au sujet de la dilatation du temps prédite par la relativité restreinte, Albert Einstein indique en 1911 :
« Si nous placions un organisme vivant dans une boîte… on pourrait s'arranger pour que cet organisme, après un temps de vol aussi long que voulu, puisse retourner à son endroit d'origine, à peine altéré, tandis que les organismes correspondants, qui sont restés dans leur position initiale auraient depuis longtemps cédé la place à de nouvelles générations. Car pour l'organisme en mouvement, la grande durée du voyage était un court instant, à condition que le mouvement ait été effectué quasiment à la vitesse de la lumière[14]. »
La même année, Paul Langevin développe cette expérience de pensée[15] : « le boulet de Jules-Verne Langevin » où il compare le temps perçu par un voyageur qui voyage à une vitesse proche de la lumière dans un boulet de canon inspiré par Jules Verne et celui passé sur la Terre à son retour. Cette description ne présente encore pas le paradoxe du paradoxe des Jumeaux, qui est que l'histoire relative des jumeaux est apparemment identique, mais leur situation finale en terme d'âge différente. En effet, ce n'était pas l'intention de Langevin et la description de Langevin est à la base dissymétrique (pas de jumeaux, on compare un voyageur et la Terre) et ne fait pas apparaître la symétrie apparente des situations[16]. Cette formulation là aurait été façonnée graduellement par plusieurs auteurs se penchant successivement sur le sujet[16].
Cet exposé, tenu lors de la Conférence au Congrès de philosophie de Bologne en 1911, fait cependant grande impression notamment au philosophe Henri Bergson qui y assiste, et permet de populariser et diffuser la notion de temps propre et d'illustrer la révolution philosophique qu'elle apporte[17].
La présentation du voyage relativiste avec des jumeaux semble faite pour la première fois en 1918 par le physicien Hermann Weyl dans son livre Raum, Zeit, Materie (Espace, Temps, Matière)[16]. C'est Max von Laue qui attire l'attention sur le paradoxe proprement dit en 1912 dans son article Deux objections à la théorie de la relativité et sa réfutation[18], en l'attribuant à Langevin[16].
Paul Painlevé est l'auteur en 1922, lors de la visite d'Einstein au Collège de France, d'une présentation particulièrement claire du paradoxe en présence d'Einstein et lance ainsi le débat sur sa résolution dans la communauté scientifique[16], qui allait faire couler beaucoup d'encre et susciter de nombreux débats.
Différentes solutions au paradoxe[modifier | modifier le code]
Introduction[modifier | modifier le code]
La conclusion largement partagée par les spécialistes est que le jumeau voyageur est plus jeune que son frère à son retour sur Terre. Les manières d'arriver à cette conclusion sont nombreuses et mettent parfois l'accent sur des éléments différents.
De temps en temps, le paradoxe n'est cité que pour mémoire. Dans les livres récents[19], le problème n'est souvent présenté que sur l'ombre d'une page, d'autres sont un peu plus diserts[20]. Le paradoxe est souvent le sujet d'exercices proposés aux étudiants abordant la relativité restreinte[21]. On citera comme sources de divers aspects des éclairages qui sont présentés ici le livre de J. H. Smith et celui de V. Ougarov[22]. Ce dernier livre contient en outre une introduction assez complète à l'Interprétation géométrique de la relativité restreinte utilisée ci-dessous pour la présentation des diagrammes de Minkowski.
D'un point de vue concret, les phases d'accélérations sont nécessaires au départ depuis la Terre, au retournement à l'arrivée au point d'éloignement maximal et à l'arrêt du voyageur en fin de course. Toutefois, la majorité des spécialistes tombe d'accord pour minimiser l'importance à attribuer aux effets de ces accélérations, mis à part pour le changement de référentiel inertiel par le jumeau voyageur. Le jumeau qui fait demi-tour ne reste pas immobile dans un référentiel inertiel. Il ne peut pas considérer que les lois de la physique restent inchangées par changement d'un référentiel non inertiel vers un référentiel inertiel. L'écart du temps qui en résulte est considéré comme dû à la non-conservation de la simultanéité lors de ce changement de référentiel.
Certains spécialistes affirment que les dilatations des durées dans le cadre du paradoxe des jumeaux sont dues aux trajets en mouvement uniforme qui peuvent être aussi longs que voulu, minimisant le rôle des accélérations quant aux valeurs numériques[20],[23]. D'autres que « en toute rigueur c'est à la relativité générale qu'il faut faire appel pour parler de ces accélérations [...] cependant on peut discuter du problème de manière satisfaisante dans le cadre de la seule relativité restreinte[24] ».
Traitement du paradoxe par longueur des lignes d'univers[modifier | modifier le code]

En relativité restreinte, calculer le temps propre d'un observateur entre deux événements revient à la mesure d'une longueur d'arc de la ligne d'univers parcourue par cet observateur entre ces deux événements[25]. Cette « longueur » n'est pas à prendre au sens habituel euclidien mais au sens de la pseudo-métrique de géométrie de Minkowski à quatre dimensions incluant le temps : c'est , l'intervalle d'espace-temps entre ces deux événements, défini par l'égalité . En abordant le problème sous cet angle, calculer le vieillissement différentiel des jumeaux revient à calculer la longueur des « chemins » parcourus par chacun d'entre eux dans l'espace de Minkowski[25].
Les chemins des jumeaux dans l'espace de Minkowski peuvent être représentés dans un diagramme de Minkowski, et forment un triangle (voir figure ci-contre). À première vue, le chemin parcouru par le jumeau voyageur est plus long que le chemin parcouru par le jumeau resté sur Terre, mais l'inégalité triangulaire dans un espace de Minkoswski est différente de celle bien connue dans l'espace euclidien. Dans l'espace minkowskien, il existe un équivalent de l'inégalité triangulaire, valable sous certains conditions vérifiées dans le cas du paradoxe (intervalles de genre temps), établissant les relations entre les longueurs des côtés d'un triangle. Pour un triangle ABC, on a alors l'inégalité dans l'espace minkowskien :
Cette inégalité est l'inverse de celle de l'espace euclidien. Dans l'espace minkowskien, un chemin faisant un détour (dans l'espace-temps) est toujours plus « court » (en termes d'intervalle espace-temps) que la « ligne droite ». Une « ligne droite » dans l'espace minkowskien est la ligne d'univers d'une particule qui n'est soumise à aucune force, donc à vitesse constante ou stationnaire.
Cette propriété permet d'illustrer et d'expliquer le paradoxe des jumeaux. Le « jumeau » restant sur Terre parcourt une « ligne droite » dans l'espace-temps AC. Le jumeau qui voyage parcourt deux segments de droites AB et BC (il fait demi-tour en B pour rejoindre son jumeau en C). Les lignes d'univers des deux jumeaux forment un triangle ABC, dont les côtés sont de genre temps (vitesse des jumeaux inférieure à celle de la lumière) et orientés vers le futur.
L'intervalle espace-temps du jumeau qui voyage est donc inférieur, selon l'inégalité triangulaire minkowskienne, à celui du jumeau stationnaire. Le temps propre du jumeau qui voyage est donc inférieur, et il est donc plus jeune au terme de son voyage que son jumeau resté sur Terre.
Les deux histoires et les deux trajectoires des deux jumeaux ne sont pas interchangeables : un seul des jumeaux est objectivement resté dans un référentiel galiléen (celui resté sur Terre), sans subir aucune accélération, et sa trajectoire correspond de manière univoque à la ligne droite. On ne peut donc inverser les deux points de vue[26].
Généralisation[modifier | modifier le code]
Cette méthode de calcul du vieillissement différentiel est valable pour toutes les lignes d'univers de genre temps, pas seulement pour les lignes droites du paradoxe des jumeaux simplifié, où les accélérations sont infinies. Même en cas d'accélération finie, menant à des angles arrondis du triangle, la même méthode reste valable en calculant les longueurs totales en intégrant les longueurs de segments de droite infinitésimaux[25],[27]. D'ailleurs une vérification expérimentale du paradoxe des jumeaux utilise cette propriété pour calculer le vieillissement différentiel d'horloges embarquées dans des avions et des horloges laissées au sol, et les décalages mesurés sont conformes à ceux attendus en utilisant cette méthode (voir confirmations expérimentales).
Cette constatation correspond à un principe de la relativité, restreinte ou générale, de vieillissement extrémal. Selon ce principe, parmi toutes les trajectoires entre deux événements de l'espace-temps, la trajectoire inertielle en relativité restreinte, ou une géodésique en relativité générale, est celle pour laquelle le temps propre vécu entre les deux événements est le plus long[28].
Cette méthode jette également un éclairage sur le rôle de l'accélération dans le paradoxe des jumeaux. L'accélération joue un rôle uniquement dans le sens où elle modifie l'allure et par conséquent la longueur des lignes d'univers, mais le paradoxe se traite uniquement en considérant la longueur des chemins parcourus, et l'accélération ne joue pas de rôle « en soi », ce qui rend le paradoxe tout à fait traitable dans le domaine de la relativité restreinte, sans faire appel à la relativité générale[25]. L'accélération joue aussi un rôle pour établir que le diagramme de Minkowski ne peut pas être dessiné également comme un triangle du point de vue du jumeau voyageur, avec un jumeau fixe paraissant faire un aller-retour. Car objectivement, seul le jumeau voyageur peut mesurer les effets de l'inertie et nous savons donc que le chemin constitué de deux segments est forcément celui du jumeau voyageur.
Par échanges de signaux et effet Doppler[modifier | modifier le code]
Cette approche a été suggérée par Langevin dès 1911[15], pour exhiber une dissymétrie entre les deux jumeaux, et résoudre le paradoxe[Information douteuse], qui n'existe que si la situation des jumeaux est considérée comme symétrique. Elle a été étudiée pour la première fois en détail par Charles Galton Darwin, en 1957[29],[30]. Cette approche met en œuvre la transmission de signaux lumineux (ou radio, voyageant à la vitesse de la lumière, vitesse maximale possible et identique dans chaque référentiel inertiel, pour la relativité restreinte), émis régulièrement (selon leur propre horloge) au même rythme convenu d'avance par chaque jumeau, à destination de l'autre. Cette approche montre que chaque jumeau va recevoir les signaux de l'autre selon une histoire différente, montrant ainsi que la situation des jumeaux n'est pas symétrique[31],[DR 1]. De plus, en comptant les signaux reçus, chaque jumeau aura une indication du temps écoulé pour l'autre jumeau : le jumeau voyageur aura eu le temps d'émettre moins de signaux que le jumeau fixe[32].
Perception et comptage des signaux[modifier | modifier le code]
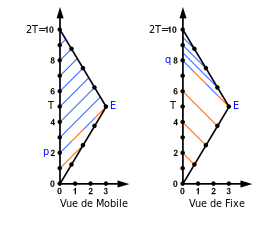
Cette approche montre que le jumeau fixe reçoit d'abord une série de signaux à un rythme régulier lent, puis (après que le jumeau mobile a fait demi-tour) à un rythme régulier beaucoup plus rapide (voir signaux « Vue de Fixe » dans le diagramme ci-contre). Le temps q, à l'horloge terrestre, après lequel le jumeau fixe reçoit les signaux à un rythme plus rapide est , si les jumeaux se rencontrent au temps 2t à l'horloge terrestre. Ce temps est d'autant plus proche du temps du retour (2t) que la vitesse du jumeau mobile est proche de la vitesse de la lumière[DR 1].
Réciproquement, le jumeau mobile fait le même constat : il constate que les signaux envoyés par le jumeau fixe lui arrivent d'abord à un rythme régulier lent, puis après qu'il a fait demi-tour, à un rythme régulier plus rapide. Le signal envoyé par le jumeau fixe, reçu au moment du demi-tour, a été envoyé au temps p de l'horloge fixe, avec , et est d'autant plus proche du temps de départ que la vitesse du voyage est proche de celle de la lumière[DR 1] ("Vue de Mobile" dans le diagramme ci-contre).
Même si les deux jumeaux font le même constat que l'autre commence à vieillir plus lentement, puis en accéléré, le jumeau fixe reçoit des signaux ralentis pendant la quasi-totalité du voyage, tandis que le jumeau mobile en reçoit pendant seulement la moitié du voyage, où il constate que le jumeau fixe a atteint l'âge p, presque égal au temps de départ. C'est la raison pour laquelle Bohm conclut l'analyse de cette approche en constatant que du point de vue du jumeau mobile, l'effet du ralentissement du temps du jumeau fixe est plus que contrebalancé par la période où son vieillissement est plus rapide, et il ne sera pas surpris de le trouver plus vieux que son âge au retour, et réciproquement[Bo 1].
Étude du vieillissement différentiel[modifier | modifier le code]

Mais on peut faire remarquer que l'observation de changement de fréquence des signaux résulte d'un effet Doppler et n'est qu'un phénomène dû à un éloignement (ou un rapprochement) et une vitesse de transmission des signaux finie, qui ne témoigne pas forcément d'un écoulement différent du temps. Tout comme l'audition de fréquences aiguës, puis graves, pour un effet Doppler acoustique, ne témoigne pas d'un changement dans l'écoulement du temps.
Les différences de perception des signaux entre les deux jumeaux suffisent à mettre en évidence une asymétrie, ce qui est un des buts recherchés, mais il faut rendre compte de la différence d'âge qu'auront réellement les deux jumeaux au retour du jumeau mobile.
Un point important est qu'un jumeau n'a aucun moyen direct de connaitre le temps que vit l'autre jumeau, tout ce qu'il peut faire est de calculer le temps simultané théorique de l'autre jumeau[Bo 2]. En relativité restreinte, les événements définis comme simultanés à un observateur sont ceux compris dans un hyperplan (à trois dimensions), « orthogonal »[34] à la ligne d'univers de l'observateur. Sur un diagramme de Minkowski, réduit à deux dimensions, cet « hyperplan orthogonal » est représenté par une droite perpendiculaire à la ligne d'univers de l'observateur, si l'observateur est fixe (ligne verticale), mais si on considère une ligne d'univers correspondant à un mouvement, son hyperplan de simultanéité ("orthogonal") est représenté par une droite oblique par rapport à cette deuxième ligne d'univers[35].
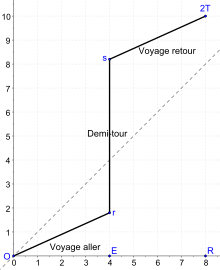
Un moyen de rendre compte du vieillissement différentiel est de « suivre » l'âge du jumeau fixe « simultané » à l'âge du jumeau mobile[36], indépendamment de la propagation de signaux et de l'effet Doppler, par l'utilisation des plans de simultanéité.
Sur le diagramme ci-contre à droite, les lignes de simultanéité du jumeau mobile sont en bleu lors du voyage aller, et en rouge lors du voyage retour. Quand le jumeau mobile arrive au point de demi-tour E, l'âge simultané du jumeau fixe est , moins avancé que le jumeau mobile, et compatible du fait que - d'un point de vue relativiste - c'est le jumeau fixe qui est en mouvement par rapport au jumeau mobile et vieillit donc plus lentement. Mais, après le demi-tour du jumeau mobile, l'âge « simultané » du jumeau fixe a augmenté soudainement jusqu'à la valeur , bien supérieur à l'âge actuel du jumeau mobile : dans son nouveau référentiel, les plans de simultanéité (lignes en rouge) ont des orientations nettement différentes de celles du précédent (lignes en bleu). Cela illustre la relativité de la simultanéité, qui n'est pas une notion absolue en relativité, mais qui dépend du mouvement relatif des objets considérés. Ensuite, l'âge du fixe vu du mobile augmente de nouveau plus lentement que l'âge du mobile, de la même manière et symétriquement au voyage aller, mais ne pourra jamais compenser le grand différentiel qui rend compte de la différence d'âge des deux jumeaux au retour[Bo 1],[DR 1].
Autre approche[modifier | modifier le code]
Une approche de la résolution du paradoxe des jumeaux par l'effet Doppler a été réalisée par Hermann Bondi en 1964, à partir de sa méthode didactique de présentation de la relativité restreinte, dite en anglais Bondi k-calculus.
Paradoxe des jumeaux et mouvement accéléré[modifier | modifier le code]
Rôle de l'accélération dans l'étude du paradoxe en relativité restreinte[modifier | modifier le code]
Dans le cadre des études du paradoxe en relativité restreinte (espace-temps plat, possédant une géométrie de Minkowski), les auteurs insistent sur le fait que les accélérations que subit le jumeau mobile n'ont pas d'influence directe sur la différence d'âge. L'influence est indirecte, car l'accélération est indispensable pour que le jumeau mobile passe d'un référentiel galiléen à un autre (du trajet aller, au trajet retour), et ce sont les différences de chemin induites par ce changement de référentiel subi par un seul jumeau qui sont directement responsables de vieillissement asymétrique, et de sa quantité. De ce fait, le paradoxe peut être traité dans le cadre de la relativité restreinte[32],[37],[38],[Pe 1],[Sa 1].

Veselin Petkof énumère trois raisons majeures justifiant le fait que l'accélération ne joue pas de rôle direct dans le paradoxe des jumeaux[Pe 1] :
1) L'"hypothèse de l'horloge" (clock hypothesis), largement utilisée en relativité restreinte, par exemple pour traiter des systèmes en rotation, suppose que l'effet total d'une accélération sur une horloge dite « idéale » est égal à l'intégrale des effets de relativité restreinte produits par les changements de vitesse infinitésimaux. L'accélération en elle-même n'ajoute aucun effet.
2) Il existe une version « des trois horloges » du paradoxe des jumeaux, dans laquelle il n'existe aucune accélération, et pourtant un vieillissement différentiel, et le même que celui avec accélération, a bien lieu. Au lieu d'un jumeau voyageur qui accélère quatre fois durant son voyage, on considère deux horloges H1 et H2, voyageant à vitesse constante. H1 fait le voyage « aller », et H2 le « retour ». Une horloge H est fixe. L'horloge H1 passe au même endroit que H à un certain temps T=0 de l'horloge H, et H1 est synchronisée avec H. H1 intercepte la trajectoire de H2 (qui va en sens inverse) au point de retour du jumeau voyageur. On profite de ce que H1 et H2 sont au même endroit pour synchroniser H2 sur H1. H2 finit par revenir au point de l'horloge H, et on compare les deux horloges à ce moment. Les calculs montrent que la différence de temps entre H et H2 est la même que la différence d'un jumeau voyageur ayant accéléré avec une accélération infinie (pour suivre les mêmes lignes d'univers que H1 et H2, en forme de triangle).
3) Une autre version du paradoxe des jumeaux introduit un deuxième jumeau voyageur qui effectue deux voyages aller-retour au lieu d'un seul, en accélérant donc huit fois au lieu de quatre, avec chacune la même intensité, la même accélération, que le jumeau voyageur original. La distance du voyage (plus courte) du second jumeau voyageur est calculée de manière que les deux jumeaux voyageurs retournent sur terre en même temps, l'un après un voyage, l'autre après deux voyages. Les calculs montrent que les deux jumeaux voyageurs ont vieilli exactement de la même manière, bien que l'un ait subi deux fois plus d'accélération que l'autre (la longueur minkowskienne des lignes d'univers des deux jumeaux voyageurs sont les mêmes).
Ce sont donc bien uniquement les longueurs des lignes d'univers parcourues qui déterminent l'écoulement du temps propre, et l'accélération n'a d'influence que parce qu'elle agit sur la forme, et donc la longueur, des lignes d'univers. Voir également à ce sujet le paragraphe Généralisation du traitement du paradoxe par inégalité triangulaire.
Études du paradoxe en relativité restreinte, avec des accélérations finies[modifier | modifier le code]
Les présentations ci-dessus sont souvent critiquées car si elles révèlent bien l'asymétrie des observateurs Fixe et Mobile, puisque l'un va changer de référentiel lors de son changement de sens, la présentation néglige totalement le côté physique du saut. En particulier, quel est le comportement de l'horloge de Mobile lors de ce retournement ?
Une solution usuelle consiste à traiter l'aller et retour de Mobile comme un voyage comportant des phases d'accélération, pour quitter Fixe, puis se retourner en A et finalement se trouver au repos auprès de son frère, permettant ainsi une comparaison des horloges à tête reposée.
Les phases d'accélération peuvent bien sûr être séparées par des phases de mouvement rectiligne uniforme (aussi longues que l'on veut) pour lesquelles les dilatations des durées analysées ci-dessus sont directement applicables. De plus les durées d'accélération (vues par le référentiel mobile et par le référentiel fixe) sont reliées par une généralisation des formules ci-dessus, à savoir par exemple pour la phase d'accélération de départ, entre les instants 0 et du référentiel de la Terre:
où est le facteur de correction relativiste correspondant à la vitesse (uniforme) qu'a acquise Mobile à l'instant t et qu'il conserve durant la durée , accompagnant son référentiel galiléen coïncidant.
En ce sens là la relativité restreinte est parfaitement capable de traiter des problèmes où interviennent des accélérations. Il n'en reste pas moins que se pose le problème du comportement de l'horloge lors du changement de référentiel brusque, mais à la limite infinitésimal, lié au passage d'un référentiel galiléen coïncidant à celui qui lui est infiniment proche. Il s'agit là d'un postulat que l'on accepte souvent implicitement[39]. Les expériences concernant la dilatation des durées des horloges embarquées dans des avions, ou plus généralement les prévisions (vérifiées) d'effets apparaissant dans le cas de référentiels accélérés (précession de Thomas) ont validé ce postulat.
Confirmations expérimentales[modifier | modifier le code]
L'expérience de Hafele-Keating est considérée comme une confirmation expérimentale du paradoxe des jumeaux[27]. Dans cette expérience, des avions à réaction embarquent des horloges atomiques, faisant deux fois le tour de la Terre, tandis que des horloges identiques restent au sol. Un voyage a été fait dans le sens de rotation de la Terre, et un autre voyage dans le sens inverse. Un décalage temporel, différent en fonction du sens du voyage, est constaté entre les horloges embarquées et les horloges du sol, et ces décalages sont conformes aux prédictions de la relativité restreinte et générale[27].
L'interprétation de cette expérience par rapport au paradoxe des jumeaux est difficile, car les lignes d'univers des avions et des horloges fixes dans cette expérience diffèrent notablement des lignes d'univers des jumeaux. De plus, il existe d'autres effets que ceux mis en œuvre dans le paradoxe des jumeaux justifiant du décalage des horloges comme le ralentissement temporel dû à la gravitation. Dans le paradoxe des jumeaux, les lignes d'univers représentent un triangle, avec un côté représentant la ligne d'univers du jumeau fixe, et les deux autres côtés la ligne d'univers du jumeau voyageur, représentant son aller et son retour (voir Espace de Minkowski#Inégalité triangulaire). Dans l'expérience d'Hafele-Keating les lignes d'univers des horloges fixes et mobiles sont plutôt des hélices, du fait de la rotation de la Terre elle-même pour l'horloge « fixe » et la rotation autour de la Terre pour l'horloge mobile[27].
Toutefois, un des enseignements du paradoxe des jumeaux est que les différences de temps entre les horloges peuvent se calculer en fonction de la différence des longueurs (intervalle d'espace-temps) des lignes d'univers des horloges à comparer. Ceci est aussi bien valable que les lignes d'univers soient des triangles ou des hélices. La longueur des intervalles d'espace-temps a été calculée en fonction des trajectoires simplifiées des avions et mène à une différence théorique de nanosecondes pour le voyage vers l'est (même sens que la rotation de la Terre)[27], T' étant le temps de l'horloge mobile. Les effets temporels théoriques de la gravitation apportent une correction inverse , ce qui laisse une différence nette théorique de . La valeur expérimentale obtenue est , compatible avec les marges d'erreur[27].
Le voyage en sens inverse (sens contraire à la rotation de la Terre) génère des lignes d'univers différentes, avec cette fois ci une ligne d'univers (hélice) pour l'avion plus proche de la ligne droite que l'hélice de l'horloge fixe. C'est un cas où la relativité prédit [27]. Le calcul théorique des différences de ligne d'univers donne nanosecondes, avec le même effet gravitationnel en plus, ce qui donne un total théorique de . La valeur expérimentale obtenue est nanosecondes[27].
Représentations dans les arts[modifier | modifier le code]
Ce paradoxe est utilisé dans le film La Planète des singes de Franklin J. Schaffner (1968), adapté du roman de Pierre Boulle.
En 2014, le film de science-fiction Interstellar réalisé par Christopher Nolan met également en application le paradoxe des jumeaux. Cette œuvre cinématographique raconte l'histoire d'un père devant partir dans l'espace afin de trouver une planète habitable, et de ses enfants restant sur Terre. Les enfants vieillissent alors que lui presque pas. Le père a 35 ans lors de son départ, et le même âge lors de son retour ; alors que sa fille, restée sur Terre, avait 10 ans lors du départ, et a 97 ans lors du retour.
Notes et références[modifier | modifier le code]
- Schémas d'après Tatsu Takeuchi An illustrated Guide to Relativity Cambridge University Press 2010, p. 149.
- « Validation des principes de la relativité restreinte », sur École normale supérieure de Lyon (consulté le )
- Tonnelat, Chap. VII, §9.
- Al Kelly, Challenging Modern Physics : Questioning Einstein's Relativity Theories, Brown Walker Press, 2005.
- J. Terrel, « Relativistic observations and the clock problem », Nuovo Cimento, 1960, p. 457 ; H. Arzeliès, La Cinématique Relativiste, Gauthier-Villars, 1955 ; H.E. Ives, Nature, 1951, 168, 246.
- Voir aussi A. Einstein, « Dialog über Einwände gegen die Relativitätstheorie », Die Naturwissenschaften 48, pp. 697-702, 29 November 1918.
- Voir p. 933, 2e §, de Herbert Dingle, « A Problem in Relativity Theory », Proc. Phys. Soc., vol. 69, (lire en ligne). Voir également la réponse de W.H. MacCrea, « A Problem in Relativity Theory: Reply to H. Dingle », Proc. Phys. Soc., vol. 69, (lire en ligne).
- Herbert Dingle, Nature, 1957, 179, 806 ; E.G. Cullwick, Electricity and Magnetism, Longmans Green Consp., 1957, p. 70.
- Václav Hlavaty, « Criticism of the twin paradox », Mededelingen van de Koninklijke Vlaamse Academie voor Wetenschappen, vol. XXVIII, no 9, , p. 1.
- V.A. Fock, The Theory of Space Time and Gravitation, Pergamon Press, 1959.
- Jean Chazy, Théorie de la relativité et de la mécanique céleste, vol. II, Gauthier-Villars, .
- René Dugas, Histoire de la mécanique, Dunod, , p. 481.
- M. Born, Einstein's Theory of Relativity; W. Pauli, Theory of Relativity, Dover, p. 152; R.C. Tolman, Relativity, Thermodynamics and Cosmology, p. 194.
- (en) Albert Einstein, 1911, cité par (en) Robert Resnick et David Halliday, Basic Concepts in Relativity, New York, Macmillan, .
- (fr)Paul Langevin, « L’évolution de l’espace et du temps », Scientia, no 10, , p. 31-54 (lire en ligne).
- Langevin ou le paradoxe introuvable, par Élie During, dans le numéro d'avril 2014 de la Revue de métaphysique et de morale.
- (fr) Michel Paty, « Paul Langevin (1871-1946), la relativité et les quanta », Bulletin de la Société Française de Physique, no 119, , p. 15-20 (lire en ligne).
- Max von Laue, Zwei Einwände gegen die Relativitätstheorie und ihrer Widerlegung, Physikalische Zeitschrift, 13, 1912, pp. 118-120 ; Das Relativitätsprinzip, Braunschweig, F. Vieweg, 1913 (2e éd.), pp. 43 et 57-58.
- Hans Stephany, Relativity, Cambridge University Press, 3e édition (2004) (ISBN 0-521-01069-1).
- M. Lambert, Relativité restreinte et électromagnétisme, Ellipses, Paris (2000), p. 101 le paradoxe des jumeaux.
- Charles W. Misner, Kip S. Thorne, John Archibald Wheeler, Gravitation, édition Freeman, New York (1973), § 6 Accelerated Observers.
- V. Ougarov, Théorie de la relativité restreinte, édition MIR, Moscou (1974), § 59 Paradoxe des jumeaux.
- J.-M. Vigoureux, L'univers en perspective, Relativité restreinte, Ellipses, Paris (2006), p. 119 le rôle du demi-tour de la fusée.
- Smith 1997, chapitre 6 Paradoxe des jumeaux, p. 94.
- Roger Penrose A la découverte des lois de l'univers Odile Jacob, 2007, paragraphe 18.3.
- Nerlich, Graham. How the Twins Do It: STR and the Clock Paradox. Analysis, vol. 64, no. 1, 2004, pp. 21–29. JSTOR p. 23
- Eric Gourgoulhon Special Relativity in General Frames Springer, 2013, p. 54-57.
- E.F. Taylor, J.A. Wheeler Exploring Black Holes. Introduction to General Relativity, Addison Welsley, 2000, paragraphe 3-4.
- John B. Kogut Introduction to Relativity Harcourt Academic Press 2001, p. 38.
- C.G. Darwin The Clock Paradox in Relativity Nature 180, 976 (1957).
- H. Arzeliès, La cinématique relativiste, Gauthier-Villars, Paris (1955), § 96 Le voyageur de Langevin.
- Claude Semay, Relativité Restreinte, bases et applications, Dunod, , p. 64-67.
- Smith 1997, chapitre 6 Paradoxe des jumeaux, p. 96-98.
- l'orthogonalité étant définie par le produit scalaire de l'espace de Minkowski.
- La droite orthogonale dans un espace de Minkowski n'est pas forcément à angle droit par rapport à la ligne d'univers, comme dans un espace euclidien. Elle est à angle droit pour les lignes d'univers fixes (verticales), mais forme un angle de plus en plus réduit avec la ligne d'univers, à mesure que la ligne d'univers se rapproche de la vitesse de la lumière.
- L'âge « simultané » est l'âge du jumeau fixe calculé comme simultané, selon le plan de simultanéité du jumeau mobile orthogonal à sa ligne d'univers.
- Richard T.W. Arthur Minkowski Proper Time and the Status of the Clock Hypothesis, in Space, Time, and Spacetime, Springer, 2010, p. 164.
- Andrew M. Steane The Wonderful World of Relativity Oxford University Press, 2011, p. 163.
- Y. Simon Relativité restreinte, Vuibert, Paris (2004) (ISBN 2-7117-7099-0).
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- [Langevin 1911] Paul Langevin, « L'évolution de l'espace et du temps », Revue de métaphysique et de morale, t. XIX, no 4, , p. 455-466 (lire en ligne)
- Paul Langevin, « L'évolution de l'espace et du temps », Scientia, no 10, , p. 31-54 (OCLC 495031433, lire en ligne) :
- [Laue 1912] (de) Max von Laue, « Zwei Einwände gegen die Relativitätstheorie und ihrer Widerlegung » [« Deux objections à l'encontre de la théorie de la relativité et leur réfutation »], Physikalische Zeitschrift, t. XIII, , p. 118-120 (OCLC 459462566, BNF 32353331, lire en ligne).
- James H Smith, Introduction à la relativité, Masson, (1re éd. 1968), 318 p. (ISBN 2-225-82985-3)
- Mathieu Rouaud, Voyage pour Proxima : Le paradoxe des jumeaux en bande dessinée, Querrien, Mathieu Rouaud, , 96 p. (ISBN 978-2-9549309-7-8, lire en ligne)
- (en) T.A. Debs & M. Redhead The twin « paradox » and the conventionality of simultaneity, Dept. of History of Science, Cambridge University (lire en ligne):
- p. 385.
- Marie-Antoinette Tonnelat, Histoire du principe de Relativité, Flammarion,
- David Bohm, The Special Theory of Relativity, Routledge, (1re éd. 1965):
- p. 131.
- p. 129.
- Leo Sartori, Understanding Relativity, (œuvre littéraire), UC Press, :
- p. 193.
- Vesselin Petkov, Relativity and the Nature of Spacetime (2d edition), Springer, :
- p. 148.
- p. 149.
- [Borella 1996] Vincent Borella, « À propos du paradoxe de Langevin », Philosophia Scientiæ, vol. 1, no 1, , p. 63-82 (lire en ligne [PDF]).
- [During 2014] Élie During, « Langevin ou le paradoxe introuvable », Revue de métaphysique et de morale, vol. 84, no 4, , p. 513-527 (OCLC 7293634628, DOI 10.3917/rmm.144.0513, JSTOR 24311679, résumé, lire en ligne).
Articles connexes[modifier | modifier le code]
- Voyage relativiste
- Expérience de Hafele-Keating
- Intervalle d'espace-temps
- Relativité restreinte
- Relativité générale
Autres paradoxes en physique :






































