Tests de la relativité restreinte
Les tests de la relativité restreinte sont une suite d'expériences qui a commencé à la fin du XIXe siècle et qui se poursuit toujours, avec une précision toujours accrue. Ils ont été d'une importance fondamentale pour la formulation et l'acceptation de la relativité restreinte, théorie qui joue un rôle fondamental dans la description de pratiquement tous les phénomènes physiques, tant que la gravitation et les effets quantiques y jouent un rôle négligeable. Contrairement à une idée largement répandue, la relativité restreinte n'est pas seulement le résultat d'expériences de pensée, ni même de celui d'une seule expérience, comme la célèbre expérience de Michelson-Morley. Sa force réside bien plus dans le fait qu'elle est la seule qui puisse expliquer des expériences fondamentalement différentes sans la moindre contradiction. Les seuls domaines échappant à la relativité restreinte sont ceux où la gravitation ne peut être négligée, et nécessite l'usage de la relativité générale, et peut-être encore dans le domaine de la physique des neutrinos, très difficilement abordable sur le plan expérimental. Parmi les ouvrages sur les divers tests, on peut citer ceux de Jakob Laub[1], de Zhang[2], de Mattingly[3], de Clifford Martin Will (en)[4], ainsi que de Roberts, Schleif et Dlugosz[5].
La théorie de la relativité restreinte utilise un espace de Minkowski « plat ». Dans les cas où la gravitation joue un rôle non négligeable, il faut utiliser la théorie de la relativité générale, utilisant un espace « courbé », et qui repousse les difficultés jusqu'à des dimensions de l'ordre de la longueur de Planck (~1,6 × 10−35 m) inaccessibles expérimentalement à l'heure actuelle. Un article est consacré aux tests expérimentaux de la relativité générale.
Réfutations de la notion d'éther[modifier | modifier le code]
La théorie dominante au XIXe siècle est celle d'un éther au repos, milieu au sein duquel se propage la lumière, de même que le son se propage dans l'air. Il s'ensuit que la vitesse de la lumière est constante dans toutes les directions, et indépendante de la vitesse de la source. Un observateur en mouvement dans l'éther doit cependant détecter les effets d'un « vent d'éther », de la même manière qu'un observateur en mouvement dans l'air sent un « vent apparent ».
Expériences du premier ordre[modifier | modifier le code]
On a alors conduit une série d'expériences d'optique qui, malgré leur relative imprécision, auraient dû conduire, si l'éther était absolument au repos, à un résultat positif de l'ordre v/c où v est la vitesse de l'observateur et c celle de la lumière. Mais ces expériences ont donné des résultats négatifs. Ce problème est résolu par Augustin Fresnel, en 1818, par l'introduction d'une hypothèse supplémentaire : la matière entraîne l'éther à une vitesse égale à la sienne multipliée par un « coefficient d'entraînement », dépendant de l'indice de réfraction. La nécessité d'introduire ce coefficient est montrée par l'expérience de Fizeau (1851). Plus tard, Wilhelm Veltmann (de) montre que dans cette hypothèse, toutes les expériences d'optique doivent conduire à un résultat négatif au premier ordre[1].
À côté de cela, on a conduit des expériences d'électrodynamique. Elles ont aussi donné un résultat négatif, ce que ne peut expliquer la théorie de Fresnel. Hendrik Lorentz, en 1892 et 1895, introduit plusieurs variables auxiliaires pour des observateurs en mouvement, ce qui a aussi pu expliquer les résultats négatifs. Par exemple, il y a une variable de lieu, selon laquelle les champs électrostatiques se contractent dans la direction du mouvement, ainsi qu'une variable de temps, le « temps local », selon laquelle les coordonnées de temps pour un observateur en mouvement dépendent de sa position. Ceci pouvait assurer que toutes les expériences optiques et électrodynamiques donneraient un résultat négatif au premier ordre[1].
Expériences du second ordre[modifier | modifier le code]


Cependant, la théorie de Fresnel-Lorentz de l'éther au repos doit conduire à des résultats positifs dès que la précision des expériences atteint le deuxième ordre en v/c, soit (v/c)² = v²/c². La première expérience de ce type est celle de Michelson-Morley (1881 et 1887) dans laquelle un rayon est séparé en deux à angle droit, et ces rayons sont réunis grâce à un miroir semi-transparent. On peut ainsi mesurer la différence de vitesse de la lumière entre les directions perpendiculaires, par un déplacement des franges d'interférence entre les deux rayons. Mais le résultat est à nouveau négatif. Une solution est proposée par George FitzGerald en 1889 et par Lorentz en 1892 : la matière (qui définit la géométrie de l’expérience) se contracterait dans le sens du mouvement par rapport à l'éther. Autrement dit, l'ancienne hypothèse de contraction des champs électrostatiques est étendue aux forces intermoléculaires qui déterminent la dimension de la matière. Ceci serait plausible si ces forces étaient de nature élecrostatique. Mais il n'existe aucune raison théorique convaincante pour qu'il en soit ainsi. Cette hypothèse est donc considérée comme ad hoc.
Outre l'expérience optique de Michelson-Morley, un équivalent électrodynamique a été fait : l'expérience de Trouton-Noble. Elle prédit qu'un condensateur en mouvement doit subir un couple de torsion. De même, les expériences de Rayleigh et Brace tentent d'estimer la contraction de la matière prédite par Lorentz. La contraction d'une matière dans une direction cause normalement une biréfringence. L'expérience de Trouton-Rankine (en) (1908) compare la résistance de 4 bobines d'orientations perpendiculaires, au moyen d'un pont de Wheatstone. Si la contraction existe, les résistances des bobines dépendent de leur mouvement par rapport à l'éther[6],[1]. De nouveau, les résultats de toutes ces expériences sont négatifs.
Pour expliquer le résultat négatif de toutes ces expériences jusqu'à 1904, Lorentz développe sa théorie en introduisant la transformation de Lorentz complète. Henri Poincaré déclare en 1905 que l'impossibilité de démontrer un mouvement absolu, par rapport à l'éther, semble être une loi de la nature, qu'il appelle le « principe de relativité ».
Réfutations de l'entraînement complet de l'éther[modifier | modifier le code]
L'idée que l'éther pourrait être complètement entraîné par la Terre, et alentour, ce qui pourrait expliquer le résultat négatif des expériences sur l'entraînement de l'éther, a été réfutée par Oliver Lodge en 1893 au moyen de lourds disques tournants. De plus, l'expérience de Hammar (en) de 1935[n 1], l'effet Sagnac et l'existence de l'aberration de la lumière contredisent cette hypothèse, tout comme l'expérience de Michelson-Gale-Pearson, qui mesure l'effet Sagnac dû à la rotation de la Terre.
Relativité restreinte[modifier | modifier le code]
Situation de départ[modifier | modifier le code]
Albert Einstein montre en 1905 que l'ensemble des modèles et des expériences suivants :
- les équations de Maxwell-Lorentz de l'électrodynamique (indépendance de la vitesse de la lumière par rapport à celle de la source) ;
- le fait que l'induction électromagnétique ne dépend que du mouvement relatif ;
- le résultat négatif des expériences sur l'entraînement de l'éther (impliquant l'absence de repère priviliégié) ;
- l'aberration de la lumière et l'expérience de Fizeau (impliquant l'absence d'entraînement complet de l'éther) ;
ne peuvent s'intégrer dans un tout logique que si l'on suppose la constance de la vitesse de la lumière dans tous les référentiels inertiels ainsi que le principe de relativité. Le résultat en est la théorie de la relativité établie en 1905 (qui sera plus tard dénommée « relativité restreinte » en opposition à la relativité générale), où les concepts d'espace et de temps sont soumis à une révision fondamentale, et où les transformations de Galilée sont remplacées par les transformations de Lorentz. Ces transformations ne sont plus une collection de variables auxiliaires, comme le proposait Lorentz, mais concernent une symétrie fondamentale de l'espace-temps, qui se trouve à la base de théories aux prédictions remarquables comme l'électrodynamique quantique ou l'interaction électrofaible. Elle élimine toute notion d'éther, tout en faisant un grand nombre de prédictions, comme[7] :
| Principe de relativité | Constance de la vitesse de la lumière | Dilatation du temps |
|---|---|---|
| Tout observateur en mouvement uniforme dans un système inertiel ne peut pas déterminer son état de mouvement par une expérience se déplaçant avec lui. | Dans tous les repères inertiels, la vitesse de la lumière mesurée est égale dans toutes les directions (isotropie), indépendante du mouvement de la source, et ne peut pas être dépassée par un corps en mouvement. | La fréquence d'une horloge C (n'importe quel système périodique), se déplaçant entre deux horloges synchrones A et B au repos dans un système inertiel retarde par rapport à elles. |
| En outre, d'autres effets relativistes tels que la contraction des longueurs, l'effet Doppler, l'aberration relativiste et les prédictions expérimentales de théories relativistes comme le modèle standard peuvent être mesurées. | ||
Expériences fondamentales[modifier | modifier le code]
Les effets de la relativité restreinte peuvent être déduits des trois types suivants d'expériences (dont il existe de nombreuses variantes qui ont été faites, et sont toujours améliorées)[8] :
- l'expérience de Michelson-Morley, qui teste l'isotropie de la vitesse de la lumière ;
- l'expérience de Kennedy-Thorndike, qui teste l'indépendance de la vitesse de la lumière par rapport à celle de l'instrument de mesure ;
- l'expérience d'Ives-Stilwell, qui teste la dilatation du temps.
La combinaison de ces trois effets est importante, car chacun pourrait à lui seul être interprété par diverses théories. Par exemple, l'expérience de Michelson-Morley sur l'anisotropie peut être considérée comme un test du principe de relativité, selon lequel un observateur peut se considérer comme au repos. Elle est donc compatible avec des théories satisfaisant la relativité galiléenne, comme les théories de l'émission, ou celle de l'entraînement complet de l'éther, qui contiennent aussi une sorte de principe de relativité. Ce n'est que par l'addition des autres expériences comme celle d'Ives-Stilwell qu'on peut exclure les théories galiléennes. Au bout du compte, il ne reste que la relativité restreinte qui peut expliquer l'ensemble de ces expériences.
Isotropie de la vitesse de la lumière[modifier | modifier le code]
Interféromètres, résonateurs, comparaison d'horloges[modifier | modifier le code]

De nouvelles variantes des expériences de Michelson-Morley (MM) et de Kennedy-Thorndike (KT) ont été conduites pour tester l'isotropie de la vitesse de la lumière. Contrairement à MM, KT[n 2] utilisent des longueurs de bras différentes, et les mesures durent plusieurs mois, afin d'utiliser le changement de direction de la vitesse de la Terre autour du Soleil. Dans les expériences récentes utilisant des faisceaux laser stabilisés par des cavités optiques résonnantes, on peut abaisser l'incertitude sur l'anisotropie de la vitesse de la lumière vers 10-17 (MM) ou 10-13 (KT). En outre, en utilisant les réflecteurs lunaires, on a pu réaliser des variantes de KT.
Un autre type d'expérience d'isotropie est une variante de l'expérience d'Ives-Stilwell, où l'anisotrope de l'effet Doppler sur un disque en rotation est mesurée en utilisant l'effet Mössbauer. On peut aussi utiliser ces expériences pour mesurer la dilatation du temps (voir infra).
Isotropie de l'espace et des fréquences[modifier | modifier le code]
De plus, des expériences extrêmement précises de comparaison entre horloges (n'importe quel processus périodique peut être considéré comme une horloge) comme l'expérience de Hughes-Drever continuent à être faites. Elles ne sont pas restreintes au secteur des photons comme MM, mais déterminent les propriétés des noyaux atomiques. Une différence entre la vitesse limite des particules – ou de leurs interactions – et celle de la lumière se traduirait par des déviations des niveaux d'énergie des noyaux atomiques. La précision avec laquelle une anisotropie peut être exclue à ce niveau est de 10-33 GeV, ce qui donne à ces expériences la prééminence parmi les tests de la relativité restreinte. Ces expériences peuvent indifféremment être considérées comme des tests de l'anisotropie de l'espace ou des fréquences[4],[3].
Dépendance de la vitesse et de l'énergie de la source[modifier | modifier le code]
Les théories de l'émission, selon lesquelles la vitesse de la lumière dépend de celle de la source, peuvent aussi expliquer le résultat négatif des expériences sur l'entraînement de l'éther. Cependant, une série d'expériences peut exclure ce genre de théories. Par exemple, l'expérience d'Alväger qui montre que les photons ont une vitesse indépendante de celle des mésons dont ils sont issus. Également, dans l'expérience de Sagnac, les rayons lumineux ont une vitesse indépendante de la vitesse de rotation du disque. L'expérience de l'étoile double de De Sitter montre que les orbites des membres de l'étoile double n'apparaissent pas brouillées comme elles le seraient en cas de temps de propagation de la lumière variables.
D'autres observations astronomiques montrent que la propagation de la lumière ne dépend ni de la fréquence ni de l'énergie de la lumière[3].
Mesures à sens unique[modifier | modifier le code]
Une série de mesures précises de la vitesse de la lumière d'un point à l'autre, en sens unique, confirment l'isotropie de la vitesse de la lumière[5] et les prédictions de la relativité. Cependant, seule la vitesse aller-retour (de A vers B puis retour à A) peut être mesurée sans ambiguïté, car la vitesse en sens unique dépend de la méthode de synchronisation entre les horloges des extrémités. La méthode de synchronisation de Poincaré-Einstein suppose par définition la vitesse en sens unique égale à la vitesse aller-retour. Mais de nombreux modèles présentent une vitesse en sens unique anisotrope, tout en gardant la vitesse aller-retour isotrope, identique à celle donnée par la relativité restreinte. Ceci est relié au fait que la synchronisation d'Einstein est équivalente à celle obtenue par le transport suffisamment lent d'une horloge, qui rend la dilatation du temps négligeable. Cependant, parmi tous ces modèles, seule la relativité est acceptable pour la grande majorité des physiciens, car les autres sont beaucoup plus complexes, et certains (comme la théorie de l'éther de Lorentz) sont fondés sur des hypothèses extrêmes et improbables concernant des effets dynamiques destinés à masquer à l'observateur le « référentiel stationnaire ».
Dilatation du temps et contraction des longueurs[modifier | modifier le code]
La dilatation du temps, et simultanément, l'effet Doppler transverse, ont été observés directement pour la première fois dans l'expérience d'Ives-Stilwell (1938), en comparant les spectres de raie de rayons anodiques vus de devant et de derrière, avec la raie de la matière immobile. Les deux premières raies sont décalées de part et d'autre par l'effet Doppler longitudinal, avec une correction relativiste de même signe due à la dilatation du temps. La raie de la matière immobile ne se trouve plus au milieu des deux autres, ce qui conduit à un décalage du centre de gravité de l'ensemble. Par cette méthode, Ives et Stilwell aboutissent à une précision de 10-2 sur la correction de dilatation du temps. Cette précision a été bien améliorée par l'utilisation de collisionneurs à ions lourds, qui donnent une précision de 10-8. Une autre méthode est l'expérience de rotor à effet Mössbauer, où des rayons gamma sont émis au centre d'un disque tournant et mesurés en fréquence par des capteurs à effet Mössbauer disposés sur le bord. On peut aussi mesurer la dilatation du temps en observant des particules instables (muons par exemple) se déplaçant très vite, dans les rayons cosmiques ou provenant d'accélérateurs. L'expérience de Hafele-Keating a confirmé le paradoxe des jumeaux : une horloge faisant l'aller-retour entre deux points A et B immobiles l'un par rapport à l'autre retarde sur les horloges de A et de B [n 3].
La confirmation directe de la contraction des longueurs est difficile à faire en pratique, en raison de la petitesse des objets que l'on peut soumettre à des vitesses non négligeables par rapport à celle de la lumière. Cependant, il y a des confirmations indirectes : par exemple, le comportement d'ions lourds en collision à très haute énergie ne peut être expliqué qu'en considérant l'accroissement de densité dû à la contraction de leur longueur. La contraction conduit aussi à un accroissement observé de l'intensité du champ coulombien perpendiculaire à la direction du mouvement. Il en résulte que la dilatation du temps et la contraction des longueurs doivent être pris en considération pour mener des expériences sur les accélérateurs de particules.
Masse, énergie et impulsion relativistes[modifier | modifier le code]

Depuis 1901, tout un ensemble de mesures ont été faites pour vérifier si la masse des particules des rayons cathodiques dépend de leur vitesse. Les résultats ont effectivement démontré cette dépendance, cependant la précision en a été longuement contestée, et donc son utilisation pour la distinction entre diverses théories concurrentes. Finalement, de nouvelles expériences ont permis d'établir avec certitude l'accord avec les prédictions de la relativité restreinte.
Aujourd'hui, ces prédictions sont confirmées en routine dans la construction des accélérateurs de particules, comme le LEP, le RHIC ou le LHC. Les formules relativistes y sont non seulement vérifiées, mais absolument nécessaires pour comprendre le comportement et la construction des cyclotrons et synchrotrons, où les particules sont accélérées à des vitesses proches de celle de la lumière.
Sagnac et Fizeau[modifier | modifier le code]

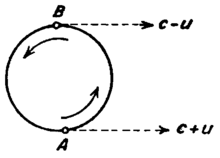
La relativité restreinte prédit que deux rayons lumineux parcourant le même circuit fermé en sens inverse parviennent en des temps différents au point d'émission/réception si ce dernier se déplace le long du circuit (ceci est une conséquence directe de l'indépendance de la vitesse de la lumière de celle de la source, (voir supra)). L'effet a réellement été observé et s'appelle l'effet Sagnac. Au début du XXIe siècle, il est nécessaire de prendre en compte cet effet dans de nombreux dispositifs expérimentaux, et notamment pour le fonctionnement correct du GPS.
Si ce genre d'expérience est mené dans des milieux en mouvement, il faut aussi considérer le coefficient d'entraînement de Fresnel, comme le montre l'expérience de Fizeau de 1851. Bien que cet effet ait été initialement interprété comme montrant l'existence d'un éther pratiquement stationnaire, ou partiellement entraîné, il peut facilement être expliqué par la relativité restreinte en utilisant sa loi de composition des vitesses : il suffit de se placer temporairement dans le système au repos de la matière, et de remarquer que la vitesse de la lumière y est de c/n où c est la vitesse de la lumière dans le vide et n l'indice de réfraction de la matière.
Théories des tests[modifier | modifier le code]
Diverses théories des tests ont été mises au point pour déterminer l'issue possible d'expériences sur la violation de la relativité restreinte dans le cas où l'on ajoute certains paramètres à la théorie existante. Par exemple, il existe les schémas de Robertson-Mansouri-Sexl (RMS) et les extensions du modèle standard (SME). RMS a trois paramètres mesurables concernant la contraction des longueurs et la dilatation du temps. On peut en déduire toute anisotropie de la vitesse de la lumière. Par contre, SME comprend beaucoup de paramètres de violation des transformations de Lorentz, non seulement pour la relativité restreinte, mais aussi pour le modèle standard et la relativité générale, c'est-à-dire un bien plus grand nombre de paramètres mesurables.
Autres tests modernes[modifier | modifier le code]
Les progrès techniques ont rendu possible depuis les années 1990 une série de mesures de haute précision. Ceci est lié aux théories modernes de la gravité quantique, qui permettent des brisures minimes de l'invariance de Lorentz. Comme une « invariance de Lorentz locale » doit avoir lieu dans des systèmes de référence en chute libre, des expériences sur le principe d'équivalence faible font aussi partie de ces tests. Les résultats sont analysés dans le cadre des théories des tests comme RMS ou plutôt SME[3].
- Outre les variations déjà évoquées des expériences de Michelson-Morley et de Kennedy-Thorndike, des expériences de Hughes-Drever sont aussi poursuivies pour tester l'isotropie dans le secteur des nucléons. Dans le secteur des électrons, on utilise des balances de torsion à polarisation du spin.
- La dilatation du temps est étudiée dans les expériences modernes par l'observation de l'effet Doppler dans le lithium, ce qui explore les secteurs des électrons, des protons, et des photons.
- D'autres expériences utilisent des pièges de Penning pour observer des déviations du mouvement cyclotron et de la précession de Larmor dans des champs électriques et magnétiques.
- Des violations de la symétrie CPT (qui représenteraient déjà une violation de l'invariance de Lorentz) peuvent être établies par des expériences sur les mésons neutres, les pièges de Penning et les muons.
- Il peut y avoir aussi des effets de seuil en énergie, pour les photons, les électrons et autres particules, que ce soit dans les observations astronomiques ou les expériences sur accélérateurs terrestres. Ceci pourrait conduire à des changements des valeurs standard pour des processus dépendant des hautes énergies, comme le rayonnement Tcherenkov dans le vide, ou des modifications du rayonnement synchrotron.
- On étudie aussi les phénomènes d'oscillations des neutrinos ou la vitesse des neutrinos, particulièrement difficiles à mettre en évidence et qui peuvent violer l'invariance de Lorentz.
- Des observations astronomiques sont conduites sur la vitesse des photons, la dispersion ou la biréfringence du vide sidéral. Ceci pourrait conduire au fait que des photons d'énergie, de fréquence ou de polarisation différentes se propagent à des vitesses différentes dans le vide, contrairement à ce qu'affirme la relativité restreinte. Ceci pourrait aussi s'observer dans le rayonnement synchrotron.
- Comme l'espace cosmique n'est pas rigoureusement vide, mais rempli par le rayonnement du fond diffus cosmologique, la relativité restreinte n'y est pas absolument satisfaite, comme le montre l'effet Greisen–Zatsepin–Kuzmin, qui freine les protons de plus de 5 × 1019 eV dans le repère où le rayonnement fossile est isotrope, qui devient à ce titre un repère privilégié. Une dispersion en fonction de la fréquence des photons se révèlerait dans l'apparence des disques d'Airy à l'observation d'étoiles lointaines ou de quasars.
- Enfin, les observations sur le boson de Higgs, qui démarrent en 2012, pourraient sensiblement modifier les théories modernes.
Conclusions[modifier | modifier le code]
La théorie de la relativité restreinte a été confirmée par de nombreuses expériences. Malgré de grands efforts, il n'a pas été possible de trouver jusqu'à maintenant des violations de l'invariance de Lorentz. Si celles-ci existent, elles ne peuvent être mises en évidence que dans des domaines difficilement accessibles en 2012, comme l'échelle de Planck, ou avec des particules difficilement détectables comme les neutrinos.
Notes et références[modifier | modifier le code]
- (en)/(de) Cet article est partiellement ou en totalité issu des articles intitulés en anglais « Tests of special relativity » (voir la liste des auteurs) et en allemand « Tests der speziellen Relativitätstheorie » (voir la liste des auteurs).
Notes[modifier | modifier le code]
- L'expérience de Hammar utilise un interféromètre où les deux rayons parcourent le même trajet en sens inverse. Sur une partie du trajet, ils sont entourés d'un lourd tuyau métallique. Au cas où le tuyau est parallèle au vent d'éther, il entraîne partiellement l'éther et diminue ce vent, ce qui accélère un rayon et ralentit l'autre. Dans une direction perpendiculaire, il n'y a pas d'effet. On doit donc observer un déplacement des franges entre les deux direction. Cela n'est pas le cas.
- L'expérience de Kennedy-Thorndike a été faite en 1932. À cette époque, les lasers n'existaient pas, et on devait utiliser des lumières émises avec un spectre de raie étroite. La meilleure source était une raie verte du mercure, dont la longueur de cohérence ne dépasse pas 32 cm, ce qui limitait considérablement la différence de longueur possible pour les deux bras de l'interféromètre. Les expériences modernes utilisent des sources laser stabilisées par des cavités optiques résonnantes, et qui ont des longueurs de cohérence bien plus grandes.
- Dans cette expérience, des effets de relativité générale peuvent se manifester en raison des accélérations. On peut éviter toute ambiguïté à cet égard en utilisant des horloges mobiles C et D se déplaçant uniformément, en observant les instants de croisement de C avec A puis B et de D avec B puis A, et en faisant la somme des intervalles de temps mesurés, tant sur les horloges mobiles C et D que sur les horloges synchrones A et B.
Références[modifier | modifier le code]
- (de) Jakob Laub, « Über die experimentellen Grundlagen des Relativitätsprinzips », Jahrbuch der Radioaktivität und Elektronik, vol. 7, , p. 405–463
- (en) Yuan Zhong Zhang, Special Relativity and Its Experimental Foundations, World Scientific, , 296 p. (ISBN 978-981-02-2749-4)
- (en) David Mattingly, « Modern Tests of Lorentz Invariance », Living Rev. Relativity, vol. 8, no 5, (lire en ligne)
- [PDF] (en) Clifford M. Will, « Special Relativity: A Centenary Perspective », dans T. Damour, O. Darrigol, B. Duplantier et V. Rivasseau, Poincare Seminar 2005, Bâle, Birkhauser, (lire en ligne), p. 33–58
- (en) T. Roberts, S. Schleif et J. M. Dlugosz, « What is the experimental basis of Special Relativity? », Université de Californie à Riverside, (consulté le )
- (en) F. T. Trouton et A. Rankine, « On the electrical resistance of moving matter », Proc. Roy. Soc., vol. 80, no 420, , p. 420 (DOI 10.1098/rspa.1908.0037)
- (en) C. Lämmerzahl, « Special Relativity and Lorentz Invariance », Annalen der Physik, Wiley, vol. 14, nos 1-3, , p. 71–102 (DOI 10.1002/andp.200410127, résumé)
- (en) H. P. Robertson, « Postulate versus Observation in the Special Theory of Relativity », Reviews of Modern Physics, APS, vol. 21, no 3, , p. 378–382 (DOI 10.1103/RevModPhys.21.378, lire en ligne)
