Orbitale atomique

En mécanique quantique, une orbitale atomique est une fonction mathématique qui décrit le comportement ondulatoire d'un électron ou d'une paire d'électrons dans un atome. Cette fonction donne la probabilité de présence d'un électron d'un atome dans une région donnée de cet atome. On la représente ainsi souvent à l'aide d'isosurfaces, qui délimitent la région à l'intérieur de laquelle la probabilité de présence de l'électron est supérieure à un seuil donné, par exemple 90 %. De telles régions ne sont pas nécessairement connexes et peuvent présenter des formes complexes issues des harmoniques sphériques.
Chaque orbitale atomique est définie par un triplet (n, ℓ, mℓ) unique de nombres quantiques qui représentent respectivement l'énergie de l'électron, son moment angulaire et la projection de ce moment angulaire sur un axe donné. Chacune de ces orbitales peut être occupée par au plus deux électrons différant l'un de l'autre par leur nombre quantique magnétique de spin ms. On parle d'orbitales s, p, d et f pour désigner les orbitales définies par un moment angulaire ℓ égal respectivement à 0, 1, 2 et 3. Ces noms proviennent d'anciennes dénominations des raies spectrales des métaux alcalins décrites comme sharp, principal, diffuse et fine ou fundamental ; les orbitales correspondant à ℓ > 3 sont ensuite nommées alphabétiquement g, h, i, k, etc.[1],[2],[3], en omettant la lettre j car certaines langues ne la distinguent pas de la lettre i[4].
Les orbitales atomiques sont les constituants élémentaires du nuage électronique, qui permet de modéliser le comportement des électrons dans la matière. Dans ce modèle, le nuage électronique d'un atome à plusieurs électrons peut être approché comme une configuration électronique formée du produit de plusieurs orbitales hydrogénoïdes. La structure du tableau périodique des éléments en blocs comprenant, sur chaque période, un total de 2, 6, 10 ou 14 éléments, est une conséquence directe du nombre maximum d'électrons pouvant occuper des orbitales atomiques s, p, d et f.

Propriétés de l'électron[modifier | modifier le code]
Nature quantique[modifier | modifier le code]
Le développement de la mécanique quantique et les observations expérimentales telles que la diffraction d'un faisceau d'électrons à travers des fentes de Young ont établi la dualité onde-corpuscule pour décrire les particules élémentaires. Ainsi, les électrons ne gravitent pas autour des noyaux atomiques sur des orbites définies comme le font les planètes autour du Soleil. En effet, ils ne peuvent être décrits comme de petites sphères solides définies par une position et une vitesse autour du noyau. Au contraire, ils doivent être vus comme des ondes stationnaires occupant un volume à l'intérieur duquel ils ont des propriétés quantiques définies et ils sont susceptibles d'interagir avec d'autres particules.
- Nature corpusculaire :
- Il ne peut y avoir qu'un nombre entier d'électrons dans un atome ;
- Un échange d'énergie entre une particule incidente, par exemple un photon, et les électrons d'un atome ne concerne toujours qu'un seul électron à l'exclusion de tous les autres, quand bien même plusieurs électrons ont une probabilité non nulle de se trouver en même temps à l'endroit où l'un d'entre eux interagit avec ce photon ;
- Un électron est pourvu d'une charge électrique définie et constante, et présente un spin dont la projection sur un axe de quantification peut valoir + 12 (spin up) ou – 12 (spin down).
- Nature ondulatoire :
- L'énergie minimum d'un électron correspond à un état comparable à la fréquence fondamentale de la vibration d'une corde, dit état fondamental ; les niveaux d'énergie supérieurs de l'électron peuvent être vus comme les harmoniques de cette fréquence fondamentale ;
- Les électrons ne sont jamais localisés en un point précis de l'espace mais se manifestent dans un volume à l'intérieur duquel la probabilité d'interagir avec eux en un point donné est déterminée par leur fonction d'onde.
Expression mathématique[modifier | modifier le code]
Les orbitales atomiques peuvent être définies plus précisément à travers le formalisme mathématique de la mécanique quantique. Dans ce cadre, l'état quantique d'un électron est la fonction d'onde Ψ qui satisfait l'équation aux valeurs propres de l'hamiltonien H, appelée aussi « équation de Schrödinger indépendante du temps », ou encore « équation des états stationnaires » : H Ψ = E Ψ, où E est l'énergie associée à cette fonction d'onde. La configuration électronique d'un atome multi-électronique est approchée par combinaison linéaire (interaction de configuration, bases) de produits de fonctions mono-électroniques (déterminants de Slater). La composante spatiale de ces fonctions mono-électroniques sont les orbitales atomiques, et la prise en compte de la composante de spin définit les spinorbitales.
L'orbitale atomique est une amplitude de probabilité de présence d'un électron autour du noyau d'un atome isolé. Cette densité de probabilité dépend du carré du module de la fonction d'onde Ψ. Celle-ci est déterminée par l'équation de Schrödinger en utilisant l'approximation orbitale, qui consiste à ignorer les corrélations entre électrons et à calculer la configuration électronique d'un atome comme produits de fonctions d'onde mono-électroniques[5]. Il s'agit cependant d'une approximation, car la distribution des différents électrons dans leurs orbitales est en réalité corrélée, les forces de London étant une manifestation de cette corrélation.
Calcul d'orbitales[modifier | modifier le code]
Les orbitales atomiques peuvent être des orbitales mono-électroniques qui sont des solutions exactes de l'équation de Schrödinger pour un atome hydrogénoïde (c'est-à-dire à un seul électron). Elles peuvent aussi être à la base du calcul des fonctions d'onde décrivant les différents électrons d'un atome ou d'une molécule. Le système de coordonnées choisi est généralement celui de coordonnées sphériques (r, θ, φ) dans les atomes et de coordonnées cartésiennes (x, y, z) dans les molécules polyatomiques. L'avantage des coordonnées sphériques est que la fonction d'onde d'une orbitale est le produit de trois fonctions ne dépendant chacune que d'une seule des trois coordonnées : ψ(r, θ, φ) = R(r) Θ(θ) Φ(φ).
La fonction radiale R(r) peut être généralement modélisée à travers trois formes mathématiques couramment employées :
- les orbitales atomiques hydrogénoïdes sont dérivées de solutions exactes de l'équation de Schrödinger pour un électron et un noyau atomique. La partie de la fonction qui dépend de la distance radiale présente des nœuds radiaux et décroît selon e-a r, a étant une constante ;
- l'orbitale de type Slater (STO) est une forme d'orbitale dépourvue de nœuds radiaux mais décroît selon r comme une orbitale hydrogénoïde ;
- l'orbitale gaussienne (GTO) est dépourvue de nœuds radiaux et décroît selon e-a r2.
Les orbitales hydrogénoïdes sont utilisées dans les outils pédagogiques mais ce sont les orbitales de type Slater qui sont préférentiellement utilisées pour modéliser les atomes et les molécules diatomiques en chimie numérique. Les molécules polyatomiques à trois atomes ou plus sont généralement modélisées à l'aide d'orbitales gaussiennes, moins précises que les orbitales de Slater mais dont la combinaison en grand nombre permet d'approcher la précision des orbitales hydrogénoïdes.
Le facteur angulaire Θ(θ) Φ(φ) génère des fonctions qui sont des combinaisons linéaires réelles d'harmoniques sphériques Ym
ℓ(θ, φ), où ℓ et m sont respectivement le nombre quantique azimutal et le nombre quantique magnétique.
Orbitales d'un atome hydrogénoïde[modifier | modifier le code]
Les orbitales sont calculées comme des nombres complexes, de sorte qu'on parle d’orbitales complexes, mais on utilise le plus souvent des combinaisons linéaires d'harmoniques sphériques choisies de telle sorte que les parties imaginaires s'annulent : les orbitales deviennent ainsi des nombres réels, et on parle d’orbitales réelles.
Orbitales complexes[modifier | modifier le code]
Chaque orbitale atomique est définie par un triplet de nombres quantiques (n, ℓ, mℓ) et peut contenir au plus deux électrons différant chacun par leur nombre quantique magnétique de spin, qui ne peut être que up ou down ; le principe d'exclusion de Pauli interdit en effet à deux électrons d'un même atome de partager le même état quantique :
- le nombre quantique principal n est un entier naturel non nul : n ≥ 1 ;
- le nombre quantique secondaire (ou nombre quantique azimutal) ℓ est un nombre entier positif ou nul vérifiant 0 ≤ ℓ ≤ n – 1 et lié à la quantification du moment angulaire de l'orbitale ;
- le nombre quantique magnétique mℓ est un nombre entier vérifiant – ℓ ≤ mℓ ≤ ℓ et lié à la quantification de la projection du moment angulaire sur un axe donné ;
- le nombre quantique magnétique de spin ms vaut – 12 ou + 12, les électrons correspondants étant couramment représentés par les symboles ↓ et ↑ ; il s'agit d'une propriété intrinsèque de l'électron, indépendante des trois autres nombres quantiques.
Le nombre quantique principal n définit la couche électronique tandis que le nombre quantique azimutal ℓ définit le type de sous-couche électronique de l'électron. Selon que ℓ vaut 0, 1, 2, 3, 4, 5, 6 ou davantage, le type de ces sous-couches est noté par les lettres s, p, d, f, g, h, i, etc.
Les sous-couches elles-mêmes sont notées en associant le nombre quantique n avec la lettre représentant le nombre quantique ℓ ; ainsi, la sous-couche correspondant à (n, ℓ) = (2, 1) est notée 2p.
La configuration électronique des atomes est notée en listant les sous-couches électroniques avec, en exposant, le nombre d'électrons sur cette sous-couche. Par construction, le nombre de sous-couches par couche électronique est égal à n, tandis que le nombre d'orbitales par sous-couche électronique s, p, d, f vaut 1, 3, 5, 7, etc. Chacune de ces orbitales pouvant contenir au plus deux électrons, le nombre maximum d'électrons par type de sous-couches s, p, d, f vaut 2, 6, 10, 14.
Orbitales complexes d'un atome hydrogénoïde par triplet de nombres quantiques (n, ℓ, mℓ) Nombres quantiques Sous-couche Nombre quantique magnétique mℓ Principal Azimutal -3 -2 -1 0 1 2 3 n = 1 ℓ = 0 1s 
n = 2 ℓ = 0 2s 
ℓ = 1 2p 


n = 3 ℓ = 0 3s 
ℓ = 1 3p 

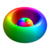
ℓ = 2 3d 




n = 4 ℓ = 0 4s 
ℓ = 1 4p 


ℓ = 2 4d 




ℓ = 3 4f 






n = 5 ℓ = 0 5s 
ℓ = 1 5p 


ℓ = 2 5d 



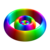
n = 6 ℓ = 0 6s 
ℓ = 1 6p 


ℓ = 2 6d 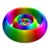




Les couleurs des surfaces représentées ci-dessus indiquent le signe des parties réelle et imaginaire de la fonction d'onde (ces couleurs sont arbitraires et ne reflètent pas une convention) :
Fonction d'onde Partie réelle Partie imaginaire Valeur positive Bleu Rouge Valeur négative Jaune Vert
Ces calculs impliquent le choix d'un axe privilégié — par exemple l'axe z en coordonnées cartésiennes — et d'un sens privilégié sur cet axe : c'est ce qui permet de définir le signe du nombre quantique magnétique mℓ. Ce modèle est par conséquent utile avec les systèmes qui partagent cette symétrie, comme dans le cas de l'expérience de Stern et Gerlach, où des atomes d'argent sont soumis à un champ magnétique non uniforme vertical.
Orbitales réelles[modifier | modifier le code]
Un atome situé dans un solide cristallin est soumis à plusieurs axes préférentiels, mais à aucune orientation préférentielle sur ces axes. Dans ces conditions, au lieu de construire les orbitales atomiques d'un tel atome à partir de fonctions radiales et d'une harmonique sphérique unique, on utilise généralement des combinaisons linéaires d'harmoniques sphériques choisies de telle sorte que leur partie imaginaire s'annule, ce qui donne des harmoniques réelles. Ce sont ces orbitales réelles qui sont généralement utilisées pour visualiser les orbitales atomiques.
Dans les orbitales hydrogénoïdes réelles, par exemple, n et ℓ ont la même signification sur leur contrepartie complexe, mais mℓ n'est plus un nombre quantique valable, bien que son module le soit. Les orbitales p hydrogénoïdes réelles, par exemple, sont données par[6],[7] :
où , et .
Les équations pour les orbitales px et py dépendent de la convention de phase choisie pour les harmoniques sphériques. Les équations précédentes supposent que les harmoniques sphériques sont définies par Ym
ℓ(θ, φ) = N eimφ Pm
ℓ(cosθ). On inclut cependant parfois[8],[9] un facteur de phase (–1)m qui a pour effet de faire correspondre l'orbitale px à une différence d'harmoniques, et l'orbitale py à une somme d'harmoniques.
Orbitales réelles d'un atome hydrogénoïde par triplet de nombres quantiques (n, ℓ, mℓ) Nombres quantiques Sous-couche Module |mℓ | du nombre quantique magnétique Principal Azimutal 0 1 2 3 n = 1 ℓ = 0 1s 
1sn = 2 ℓ = 0 2s 
2sℓ = 1 2p 
2pz
2px
2pyn = 3 ℓ = 0 3s 
3sℓ = 1 3p 
3pz
3px
3pyℓ = 2 3d 
3dz2
3dxz
3dyz
3dxy
3dx2–y2n = 4 ℓ = 0 4s 
4sℓ = 1 4p 
4pz
4px
4pyℓ = 2 4d 
4dz2
4dxz
4dyz
4dxy
4dx2–y2ℓ = 3 4f 
4fz3
4fxz2
4fyz2
4fxyz
4fz(x2–y2)
4fx(x2–3y2)
4fy(3x2–y2)n = 5 ℓ = 0 5s 
5sℓ = 1 5p 
5pz
5px
5pyℓ = 2 5d 
5dz2
5dxz
5dyz
5dxy
5dx2–y2n = 6 ℓ = 0 6s 
6sℓ = 1 6p 
6pz
6px
6pyℓ = 2 6d 
6dz2
6dxz
6dyz
6dxy
6dx2–y2n = 7 ℓ = 0 7s 
7s
Dans la représentation ci-dessus, la couleur indique le signe de la fonction d'onde, qui est positive en rouge et négative en bleu.
Géométrie des orbitales atomiques[modifier | modifier le code]
Les représentations graphiques des orbitales ont pour but de figurer les régions de l'espace que les électrons d'une orbitale atomique ont une certaine probabilité d'occuper. Ces modélisations ne peuvent représenter la totalité de la région dans laquelle l'électron est susceptible de se trouver car, en vertu des propriétés quantiques de l'électron, il existe une probabilité non nulle de le trouver à peu près n'importe où dans l'espace autour de l'atome. Par conséquent, ces représentations consistent en des isosurfaces sur lesquelles la densité de probabilité | ψ(r, θ, φ) |2 est constante et à l'intérieur desquelles la probabilité de présence de l'électron est égale à une valeur donnée, par exemple 90 %. Bien que | ψ |2 ne soit jamais négatif, on indique généralement le signe de la fonction d'onde ψ(r, θ, φ).
Il est également possible de représenter la fonction ψ et sa phase, plutôt que ψ2 qui indique la densité de probabilité mais n'a pas de phase. Les représentations de | ψ(r, θ, φ) |2 tendent à présenter des lobes moins sphériques et plus étroits que celles de ψ(r, θ, φ), mais les deux représentations ont le même nombre de lobes avec le même arrangement spatial et sont reconnaissables entre elles.
Interprétation des nombres quantiques[modifier | modifier le code]

D'une manière générale, le nombre quantique principal n détermine la taille et l'énergie de l'orbitale pour un noyau atomique donné : plus n croît, plus la taille de l'orbitale augmente. Cependant, lorsque l'on compare les orbitales de plusieurs éléments chimiques, plus le numéro atomique Z croît, plus les orbitales atomiques se contractent, car la charge électrique totale du noyau croît également avec Z. En conséquence, la taille des atomes demeure relativement constante malgré l'accumulation des couches électroniques.
Toujours d'une manière générale, le nombre quantique azimutal ℓ détermine la forme de l'orbitale, tandis que le nombre quantique magnétique mℓ détermine son orientation dans l'espace. Cependant, le nombre mℓ détermine également la forme de certaines orbitales complexes. L'ensemble des orbitales correspondant à un couple (n, ℓ) donné remplit l'espace de manière aussi symétrique que possible avec un nombre croissant de lobes et de nœuds.
Orbitales s[modifier | modifier le code]
Les orbitales s, identifiées par ℓ = 0, sont représentées par des sphères. Pour n = 1, la densité de probabilité est plus élevée au centre et décroît vers l'extérieur, mais, pour n = 2 ou plus, la densité de probabilité à l'intérieur de chaque orbitale s forme une structure ondulatoire radiale dans laquelle alternent des couches concentriques de probabilité élevée et de probabilité plus faible.
Les orbitales s sont les seules à présenter un anti-nœud, c'est-à-dire une région où la fonction d'onde a un module élevé, au centre du noyau. Les orbitales p, d, f et suivantes ont un moment angulaire et évitent le noyau, où elles présentent un nœud.
Orbitales p, d et f[modifier | modifier le code]
Les trois orbitales p pour n = 2 ont la forme de deux ellipsoïdes partageant un point de tangence au niveau du noyau atomique. Cette forme est parfois dite en haltères. Elles sont orientées orthogonalement les unes par rapport aux autres en fonction de leur nombre quantique magnétique mℓ.

Quatre des cinq orbitales d pour n = 3 ont des formes semblables, chacune avec quatre lobes en forme de poire, ces lobes étant tangents orthogonalement deux par deux, les centres de ces quatre lobes étant coplanaires. Trois de ces orbitales, nommées dxy, dyz et dxz, sont alignées sur les plans xy, yz et xz — les lobes sont situés entre chacune des trois paires d'axes de coordonnées — tandis que la quatrième, nommée dx2 – y2, est alignée sur les axes x et y eux-mêmes.
La cinquième orbitale d, nommée dz2 et correspondant à mℓ = 0, est formée de trois régions où la densité de probabilité est élevée : deux régions en forme de poire de part et d'autre du noyau le long de l'axe z et un tore autour du noyau dans le plan xy.
-
Orbitale dxy
-
Orbitale dyz
-
Orbitale dxz
-
Orbitale dx2 – y2
-
Orbitale dz2
Les orbitales f sont au nombre de sept et présentent des formes plus complexes que celles des orbitales d.
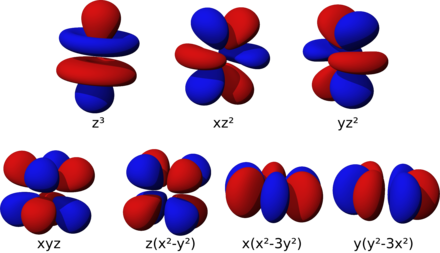
La forme des orbitales atomiques des atomes hydrogénoïdes sont issues des harmoniques sphériques. Ces formes ne sont pas uniques, et de nombreuses combinaisons linéaires sont valides, comme une transformation en harmoniques cubiques (en). Il est également possible de générer des ensembles de fonctions produisant des orbitales d ayant toutes la même forme, comme les orbitales p[10],[11].
Il convient de garder à l'esprit que toutes ces orbitales, présentées individuellement dans le cadre de modèles issus d'atomes hydrogénoïdes, coexistent simultanément dans les atomes réels.
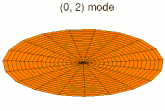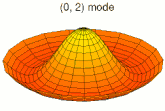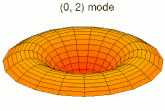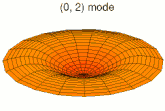
Analogie avec la vibration d'une membrane[modifier | modifier le code]
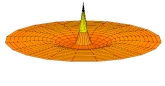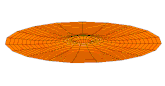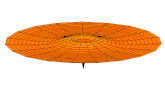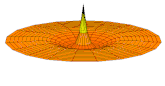
Il est possible de représenter en deux dimensions la signification des différentes formes tridimensionnelles des orbitales atomiques à l'aide des modes de vibration d'une membrane circulaire, par exemple de la peau d'un tambour[12]. Dans cette représentation, la distance par rapport au centre de la membrane équivaut à la distance de l'électron au noyau atomique, et l'amplitude de l'écart au plan d'équilibre de la membrane représente la densité de présence de l'électron dans l'atome. Cette analogie n'est pas parfaite, notamment parce que la tension d'une membrane physique comme la peau d'un tambour a pour effet d'arrondir les ondes qui la parcourent, mais elle rend compte de plusieurs propriétés qualitatives des orbitales atomiques, par exemple le fait que seules les orbitales s présentent un anti-nœud (maximum d'amplitude) au centre alors que toutes les autres présentent un nœud (amplitude nulle) à cet endroit, ou encore de visualiser la distribution géométrique des lobes des orbitales de rang élevé :
- Les 9 premiers modes de vibration de la peau d'un tambour
-
Mode u01, analogue à 1s
-
Mode u02, analogue à 2s
-
Mode u03, analogue à 3s
-
Mode u11, analogue à 2p
-
Mode u12, analogue à 3p
-
Mode u13, analogue à 4p
-
Mode u21, analogue à 3d
-
Mode u22, analogue à 4d
-
Mode u23, analogue à 5d
La partie réelle de la fonction d'onde d'orbitales atomiques s et p représentée de la même manière pour différentes valeurs de n et ℓ est ainsi analogue aux différents modes de vibration d'une peau de tambour :
- Partie réelle de la fonction d'onde d'orbitales s et p
-
Orbitale 1s
-
Orbitale 2s
-
Orbitale 3s
-
Orbitale 2p
-
Orbitale 3p
-
Orbitale 4p
Applications[modifier | modifier le code]
En physique atomique, les raies spectrales correspondent aux transitions électroniques résultant de passage d'un état quantique de l'atome à un autre. Ces états sont définis par un ensemble de nombres quantiques généralement associés à une configuration électronique, c'est-à-dire à la distribution des électrons entre les différentes orbitales atomiques. Ainsi, la configuration électronique du néon à l'état fondamental est 1s2 2s2 2p6, résumé dans le terme 1S
0.
Les orbitales atomiques sont un concept clé permettant de visualiser les processus d'excitation à l'origine des transitions électroniques. Par exemple, il est possible de relier une transition donnée à l'excitation d'un électron passant d'une orbitale occupée de nombre quantique principal n = n1 à une orbitale vacante de nombre quantique n = n2. Ainsi, l'énergie d'un électron dans un atome hydrogénoïde valant :
- ,
on peut déduire la formule de Rydberg donnant le nombre d'onde associé à une transition électronique d'une orbitale n = n1 vers une orbitale n = n2 dans un atome hydrogénoïde, où λ est la longueur d'onde, R∞ la constante de Rydberg, et Zeff la charge nucléaire effective (en) :
Appliquée à l'atome d'hydrogène, cette formule permet de calculer les raies d'émission du spectre de l'hydrogène :

Il convient cependant de garder à l'esprit que les orbitales ainsi définies sont des fonctions d'onde mono-électroniques relatives à des atomes hydrogénoïdes. Les atomes n'étant généralement pas hydrogénoïdes, ils sont au contraire poly-électroniques, de sorte que cette approximation est une manière de simplifier la modélisation de la configuration électronique des atomes, mais peut présenter des limites, notamment pour décrire les gros atomes.
Notes et références[modifier | modifier le code]
- (en) David Griffiths, Introduction to Quantum Mechanics, 1995, Prentice Hall, pp. 190–191. (ISBN 0-13-124405-1)
- (en) Ira Levine, (2000). Quantum Chemistry, 5e édition, 2000, Prentice Hall, pp. 144–145. (ISBN 0-13-685512-1)
- (en) Keith J. Laidler, John H. Meiser, Physical Chemistry, 1982, Benjamin/Cummings, p. 488. (ISBN 0-8053-5682-7)
- (en) Peter Atkins, Julio de Paula, Ronald Friedman, Quanta, Matter, and Change: A Molecular Approach to Physical Chemistry, 2009, Oxford University Press, p. 106. (ISBN 978-0-19-920606-3)
- Roger Penrose, À la découverte des lois de l'univers : La prodigieuse histoire des mathématiques et de la physique, 2004.
- (en) Ira Levine, Quantum Chemistry, 7e édition, Pearson Education, 2014, pp. 141–142. (ISBN 0-321-80345-0)
- (en) Miguel A. Blanco, M. Flórez et M. Bermejo, « Evaluation of the rotation matrices in the basis of real spherical harmonics », Journal of Molecular Structure: THEOCHEM, vol. 419, nos 1-3, , p. 19-27 (DOI 10.1016/S0166-1280(97)00185-1, lire en ligne)
- (en) Albert Messiah, Quantum mechanics: two volumes bound as one, 1999, Mineola, Dover, New-York. (ISBN 978-0-486-40924-5)
- Claude Cohen-Tannoudji, Bernard Dui, Franck Laloë, Mécanique quantique, Collection Enseignement des Sciences, Herman, Paris, 1973. Bibcode : 1973mequ.book.....C
- (en) Richard E. Powell, « The five equivalent d orbitals », Journal of Chemical Education, vol. 45, no 1, , p. 45 (DOI 10.1021/ed045p45, Bibcode 1968JChEd..45...45P, lire en ligne)
- (en) George E. Kimball, « Directed Valence », The Journal of Chemical Physics, vol. 8, no 2, , p. 188-198 (DOI 10.1063/1.1750628, Bibcode 1940JChPh...8..188K, lire en ligne)
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Lien externe[modifier | modifier le code]
- Animations, applications et recherches liées aux orbitales atomiques et à la quantification (Université Paris Sud)