Constante physique

Dépendances des constantes définissant les unités du SI depuis 2019. Ici, a → b signifie que a est utilisé pour définir b.

En science, une constante physique est une quantité physique dont la valeur numérique est fixe. Contrairement à une constante mathématique, elle implique directement une grandeur physiquement mesurable.

Les valeurs listées ci-dessous sont des valeurs dont on a remarqué qu'elles semblaient constantes et indépendantes de tous paramètres utilisés, et que la théorie suppose donc réellement constantes.

Les constantes sans dimension, comme la constante de structure fine, ne dépendent pas du système de poids et mesures utilisé. Les autres auraient évidemment des valeurs différentes dans des systèmes différents. Des systèmes (par exemple les unités de Planck) ont été proposés sur la base d'une fixation à 1 du plus grand nombre de constantes possible, mais n'ont pas connu grand succès pour le moment.

Liste de constantes physiques

Le nombre entre parenthèses représente l'incertitude sur le dernier chiffre significatif. Par exemple :

• 6,673(10) × 10⁻¹¹ signifie 6,673 × 10⁻¹¹ ± 0,010 × 10⁻¹¹ ;
• 1,602 176 620 8(98) × 10⁻¹⁹ C signifie que l'incertitude est de : 0,000 000 009 8 × 10⁻¹⁹

Constantes définissant les unités du Système international

Avant la réforme de 2019

Nom de la constante	Symbole	Origine	Valeur numérique	Incertitude relative
Vitesse de la lumière dans le vide	c (ou c0)	${\frac {1}{\sqrt {\varepsilon _{0}.\mu _{0}}}}$	299 792 458 m s−1	Exacte (définition du mètre)
Perméabilité magnétique du vide	μ0		4π  × 10-7 kg⋅m⋅A-2⋅s-2 (ou H⋅m-1) 1,256 637 061 4… × 10−6 kg m A−2 s−2	Exacte (définition de l'ampère)
Permittivité diélectrique du vide	ε0	${\frac {1}{\mu _{0}\cdot c^{2}}}$	8,854 187 817… × 10−12 A2 s4 kg−1 m−3 (ou F⋅m-1)	Exacte
Impédance caractéristique du vide	Z0	$\mu _{0}\cdot c$	376,730 313 461… kg m2 A−2 s−3	Exacte
Constante de Planck	$\ h$	Mesure	6,626 070 40(81) × 10−34 kg m2 s−1 (ou J⋅s)	1,2 × 10−8
Constante de Planck réduite	ℏ	${\frac {h}{2\pi }}$	1,054 571 800(13) × 10−34 kg m2 s−1	1,2 × 10−8
Efficacité lumineuse d'un rayonnement monochromatique défini	$K_{\mathrm {cd} }$		683 lm W−1	Exacte (définit la candela)

Depuis 2019

Nom de la constante	Symbole	Valeur numérique	Incertitude relative
Fréquence de la transition hyperfine de l'état fondamental de l'atome de césium 133	∆νCs	9 192 631 770 Hz	Exacte (définit la seconde)
Vitesse de la lumière dans le vide	c	299 792 458 m s−1	Exacte (définit le mètre)
Constante de Planck	$\ h$	6,626 070 15 × 10−34 kg m2 s−1 (ou J⋅s)	Exacte (définit le kilogramme)
Charge élémentaire	e	1,602 176 634 × 10−19 A s	Exacte (définit l'ampère)
Constante de Boltzmann	k ou kB	1,380 649 × 10−23 J K−1	Exacte (définit le kelvin)
Nombre d'Avogadro	$N_{\mathrm {A} }$	6,022 140 76 × 1023 mol−1	Exacte (définit la mole)
Efficacité lumineuse d'un rayonnement monochromatique défini	$K_{\mathrm {cd} }$	683 lm W−1	Exacte (définit la candela)

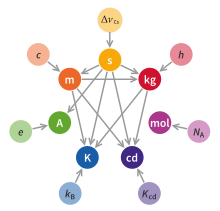
Ces constantes, fixées le 20 mai 2019, permettent à leur tour de définir les sept unités de base du Système international d'unités (seconde, mètre, kilogramme, ampère, kelvin, mole et candela). Ces nouvelles définitions améliorent le SI sans changer la valeur des unités.

Électromagnétisme

Nom de la constante	Symbole	Origine	Valeur numérique	Incertitude relative
Charge élémentaire	e		1,602 176 634 × 10−19 A s	Par définition
Constante de structure fine	α	Mesure	7,297 352 569 3(11) × 10−3	1,5 × 10−10
Perméabilité du vide	μ0	${\frac {2\alpha h}{e^{2}c}}$	1,256 637 062 12(19) × 10−6 kg m A−2 s−2	1,5 × 10−10
Permittivité diélectrique du vide	ε0	${\frac {1}{\mu _{0}c^{2}}}$	8,854 187 812 8(13) × 10−12 A2 s4 kg−1 m−3	1,5 × 10−10
Constante de Coulomb	k ou κ	${\frac {1}{4\pi \varepsilon _{0}}}$	8,987 551 792 3(15) × 109 kg m3 A−2 s−4	1,5 × 10−10
Impédance caractéristique du vide	Z0	$\ {\mu _{0}c}$	376,730 313 668(57) kg m2 A−2 s−3	1,5 × 10−10
Constante de Von Klitzing	RK	${\frac {h}{e^{2}}}$	25,812 807 459 ... × 103 kg m2 A−2 s−3	Exacte
Quantum de conductance	G0	${\frac {2}{R_{K}}}$	7,748 091 729 86 ... × 10−5 S	Exacte
Constante de Josephson	KJ	${\frac {2e}{h}}$	4,835 978 484 ... × 1014 A s2 kg−1 m−2	Exacte
Quantum de flux magnétique	Φ0	${\frac {1}{K_{J}}}$	2,067 833 848 46 ... × 10−15 Wb	Exacte
Magnéton de Bohr	μB	${\frac {eh}{4\pi m_{\mathrm {e} }}}$	9,274 010 078 3(28) × 10−24 A m2	3,0 × 10−10
Magnéton nucléaire	μN	${\frac {eh}{4\pi m_{\mathrm {p} }}}$	5,050 783 746 1(15) × 10−27 A m2	3,1 × 10−10

Gravitation

Nom de la constante	Symbole	Origine	Valeur numérique	Incertitude relative
Constante gravitationnelle	G	Mesure	6,674 30(15) × 10−11 m3 kg−1 s−2	2,2 × 10−5
Accélération normale de la pesanteur terrestre au niveau de la mer	g0	Convention	9,806 65 m s−2	Par définition

Constantes physico-chimiques

Nom de la constante	Symbole	Origine	Valeur numérique	Incertitude relative
Température du point triple de l'eau	T0	Mesure	273,16 K	3,7 × 10−7
Pression standard de l'atmosphère	atm	Convention	101 325 Pa	Par définition
Nombre d'Avogadro	NA ou L	Définition de la mole	6,022 140 76 × 1023 mol−1	Exacte
Constante des gaz parfaits	R ou R0	$k\ N_{\text{A}}$	8,314 462 618 ... J K−1 mol−1	Exacte
Constante de Boltzmann	k ou kB	Définition du kelvin	1,380 649 × 10−23 J K−1	Exacte
Constante de Faraday	F	$N_{\text{A}}\ e$	96 485,332 12 ... C mol−1	Exacte
Volume molaire d'un gaz parfait, p = 101,325 kPa, T = 273,15 K	V0	${\frac {RT}{p}}$	22,413 962 54 ... × 10−3 m3 mol−1	Exacte
Unité de masse atomique	uma		1,660 539 066 60(50) × 10−27 kg	3,0 × 10−10
Première constante de rayonnement		$c_{1}=2\pi hc^{2}$	3,741 771 852 ... × 10−16 W m2	Exacte
	pour la radiance spectrale	$c_{1L}=2hc^{2}$	1,191 042 972 ... × 10−16 W m2 sr−1	Exacte
Deuxième constante de rayonnement		$c_{2}={\frac {hc}{k}}$	1,438 776 877 ... × 10−2 m K	Exacte
Constante de Stefan-Boltzmann	σ	${\frac {2\pi ^{5}k_{B}^{4}}{15h^{3}c^{2}}}$	5,670 374 419 ... × 10−8 W m−2 K−4	Exacte
Constante radiative	a	${\frac {4\sigma }{c}}={\frac {8\pi ^{5}k_{B}^{4}}{15h^{3}c^{3}}}$	7,565 730 85... × 10−16 W m−2 K−4	Exacte
Constante de Wien	$b_{\text{énergie}}$ ou σw	${\frac {hck^{-1}}{4,965\,114\,231\,74}}$	2,897 771 955 ... × 10−3 m K	Exacte
Constante de Loschmidt	NL	${\frac {N_{\text{A}}}{V_{0}}}$	2,686 780 951 ... × 1025 m−3	Exacte

Constantes atomiques et nucléaires

Nom de la constante	Symbole	Origine	Valeur numérique	Incertitude relative
Constante de Rydberg	R∞	${\frac {m_{\mathrm {e} }\alpha ^{2}c}{2h}}$	1,097 373 156 816 0(21) × 107 m−1	1,9 × 10−12
Énergie de Hartree	EH	$2R_{\infty }hc$	4,359 744 722 207 1(85) × 10−18 J	1,9 × 10−12
Quantum de circulation		${\frac {h}{2m_{\mathrm {e} }}}$	3,636 947 551 6(11) × 10−4 m2 s−1	3,0 × 10−10
Rayon de Bohr	a0	${\frac {h}{2\pi m_{\mathrm {e} }c\alpha }}$	5,291 772 109 03(80) × 10−11 m	1,5 × 10−10
Longueur d'onde de Compton pour l'électron	λC	${\frac {h}{m_{\mathrm {e} }c}}$	2,426 310 238 67(73) × 10−12 m	3,0 × 10−10
Rayon de Compton pour l'électron	RC	${\frac {h}{2\pi m_{\mathrm {e} }c}}$	3,861 592 679 6(12) × 10−13 m	3,0 × 10−10
Rayon classique de l'électron	re	${\frac {e^{2}}{4\pi \varepsilon _{0}m_{\mathrm {e} }c^{2}}}$	2,817 940 326 2(13) × 10−15 m	4,5 × 10−10
Masse du proton	mp	Mesure	1,672 621 923 69(51) × 10−27 kg	3,1 × 10−10
Énergie du proton		Calcul	938,272 088 16(29) MeV	3,1 × 10−10
Masse du neutron	mn	Mesure	1,674 927 498 04(95) × 10−27 kg	5,7 × 10−10
Énergie du neutron		Calcul	939,565 420 52(54) MeV	5,7 × 10−10
Masse de l'électron	me	Mesure	9,109 383 701 5(28) × 10−31 kg	3,0 × 10−10
Masse du muon	mμ	Mesure	1,883 531 627(42) × 10−28 kg	2,2 × 10−8
Masse du tauon	mτ	Mesure	3,167 54(21) × 10−27 kg	6,8 × 10−5
Masse du boson Z°	mZ°	Mesure	1,625 567(38) × 10−25 kg	2,3 × 10−5
Masse du boson W	mW	Mesure	1,432 89(22) × 10−25 kg	1,5 × 10−4

Le nombre entre parenthèses représente l'incertitude absolue sur les derniers chiffres. Par exemple : 6,673(10) × 10⁻¹¹ signifie 6,673 × 10⁻¹¹ ± 0,010 × 10⁻¹¹.

Unités de Planck

Nom de la constante	Symbole	Origine	Valeur numérique	Incertitude relative
Constante de Planck	$\ h$		6,626 070 15 × 10−34 kg m2 s−1 (ou J⋅s)	Exacte
Constante de Planck réduite	ℏ	${\frac {h}{2\pi }}$	1,054 571 817 ... × 10−34 kg m2 s−1	Exacte
Masse de Planck	mP	${\sqrt {\frac {\hbar c}{G}}}$	2,176 434(24) × 10−8 kg	1,1 × 10−5
Longueur de Planck	lP	${\sqrt {\frac {\hbar G}{c^{3}}}}$	1,616 255(18) × 10−35 m	1,1 × 10−5
Temps de Planck	tP	${\sqrt {\frac {\hbar G}{c^{5}}}}$	5,391 247(60) × 10−44 s	1,1 × 10−5
Température de Planck	TP	${\sqrt {\frac {\hbar c^{5}}{Gk_{B}^{2}}}}$	1,416 784(16) × 1032 K	1,1 × 10−5
Charge de Planck	QP	${\sqrt {2ch\varepsilon _{0}}}\;$	1,875 546 037 78(15) × 10−18 C	8 × 10−11
Force de Planck	FP	${\frac {m_{P}l_{P}}{t_{P}^{2}}}={\frac {c^{4}}{G}}\;$	1,210 256(28) × 1044 N	2,3 × 10−5
Énergie de Planck	EP	$F_{P}l_{P}={\sqrt {\frac {c^{5}\hbar }{G}}}$	1,956 082(23) × 109 J	1,2 × 10−5
Puissance de Planck	PP	${\frac {E_{P}}{t_{P}}}={\frac {c^{5}}{G}}\;$	3,628 255(82) × 1052 W	2,3 × 10−5

Valeurs exactes

Dans le but de rendre l'étalonnage de l'ampère, unité de base du Système international (SI), plus précis, la 18^e Conférence générale des poids et mesures (CGPM) a adopté en 1988 des valeurs « exactes » des constantes de von Klitzing et de Josephson :

R_K = h/e² ≡ 2,581 280 7 × 10⁴ Ω (CIPM (1988) Recommandation 2, PV 56 ; 20) ;

K_J^{−1[Quoi ?]} = 2e/h ≡ 4,835 979 × 10¹⁴ Hz/V (CIPM (1988) Recommandation 1, PV 56 ; 19).

Cependant, le Comité consultatif d’électricité (CCE) a stipulé que

« les Recommandations 1 (CI-1988) et 2 (CI-1988) ne constituent pas une redéfinition des unités SI. Les valeurs de K_J et R_K, admises par convention, ne peuvent être utilisées pour la définition du volt et de l’ohm, c’est-à-dire des unités de force électromotrice et de résistance électrique du Système international d'unités. Sinon la constante µ₀ n'aurait plus une valeur définie exactement, ce qui rendrait caduque la définition de l’ampère, et les unités électriques seraient incompatibles avec la définition du kilogramme et des unités qui en dérivent. »

Nonobstant ceci, il est possible de redéfinir le kilogramme, jusqu'ici la seule unité de base du SI qui soit encore définie par un étalon physique (et est donc le seul « degré de liberté » subsistant dans le système), à partir des valeurs exactes des constantes de von Klitzing et Josephson. Si on admet cela, toute une série de constantes physiques acquièrent des valeurs exactes en conséquence.

La définition du kilogramme serait alors :

« La masse qui serait accélérée à exactement 2 × 10⁻⁷ m/s² si elle était soumise à la force par mètre entre deux conducteurs parallèles, rectilignes, de longueur infinie, de section circulaire négligeable et placés à une distance de 1 mètre l’un de l’autre dans le vide, et au travers desquels circulerait un courant électrique constant d'exactement 6 241 509 629 152 650 000 charges élémentaires par seconde. »

On en déduit alors que l'ampère vaut exactement 6 241 509 629 152 650 000 charges élémentaires par seconde. La valeur de la constante de Planck découle aussi de ces valeurs exactes, ainsi que celle de la constante de structure fine.

Voir aussi

Articles connexes

• Constante fondamentale
• Table de constantes et paramètres astrophysiques
• Comité de données pour la science et la technologie (CODATA)
• Unité de mesure, Système international d'unités, Conversion des unités

Bibliographie

• (en) Peter J. Mohr, D. B. Newell et Barry N. Taylor, « CODATA recommended values of the fundamental physical constants: 2014 », CODATA Review of moderne physics,‎ 26 septembre 2016 (lire en ligne) : discute le bien-fondé des valeurs recommandées, par les auteurs du rapport (dont Barry N. Taylor, lui-même)
• Gilles Cohen-Tannoudji et Dominique Lecourt, Les constantes universelles, Paris, Hachette littérature, coll. « pluriel », 1998, 3^e éd., 158 p. (ISBN 978-2-01-278877-0, OCLC 38552927)
• Jean-Philippe Uzan et Roland Lehoucq, Les constantes fondamentales, Paris, Éditions Belin, coll. « Histoire Sciences », 2005, 487 p. (ISBN 978-2-7011-3626-4, BNF 39295528)

Liens externes

• Bureau international des poids et mesures
• Dernier jeu de valeurs recommandées CODATA à ce jour
• CODATA (Committee on Data for Science and Technology)
• ICSU (International Council for Science)