Poussée d'Archimède

La poussée d'Archimède est la force particulière que subit un corps placé entièrement ou partiellement dans un fluide (liquide ou gaz) et soumis à un champ de gravité. Cette force provient de l'augmentation de la pression du fluide avec la profondeur ou l'altitude (effet de la gravité sur le fluide, voir l'article hydrostatique) : la pression étant plus forte sur la partie inférieure d'un objet immergé que sur sa partie supérieure, il en résulte une poussée globalement verticale ascendante. C'est à partir de cette poussée qu'on définit la flottabilité d'un corps. Cette poussée a été pour la première fois étudiée par Archimède.
Formulation du théorème d'Archimède[modifier | modifier le code]
« Tout corps plongé dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa surface libre, subit une force verticale, dirigée de bas en haut et égale (et opposée) au poids du volume de fluide déplacé. Cette force est appelée poussée d'Archimède. Elle s'applique au centre de masse du fluide déplacé, appelé centre de poussée. »
Pour que le théorème s'applique il faut que le fluide immergeant et le corps immergé soient au repos. Il faut également qu'il soit possible de remplacer le corps immergé par du fluide immergeant sans rompre l'équilibre, le contre-exemple étant le bouchon d'une baignoire remplie d'eau : si celui-ci est remplacé par de l'eau, il est clair que la baignoire se vide et que le fluide n'est alors plus au repos. Le théorème ne s'applique pas puisque nous sommes dans un cas où le bouchon n'est pas entièrement mouillé par le liquide et ne traverse pas sa surface libre.
Une fois les conditions précédentes respectées, dans un champ de pesanteur uniforme, la poussée d'Archimède, notée est donnée par la formule :
- où :
- m f est la masse du fluide contenu dans le volume V déplacé ;
- est l'accélération du champ de pesanteur.
Dans le cas particulier où la masse volumique ρ du fluide est elle aussi uniforme, on a[2] :
- où :
- V est le volume de fluide déplacé.
Si l'on considère les intensités (normes) des forces alors, en notant PA et g les normes des vecteurs associés, on a :
L'intensité PA de la poussée d'Archimède s'exprime en N, la masse volumique ρ en kg m−3, le volume de fluide déplacé V en m3 et l'accélération de la pesanteur g en m s−2.
Démonstration[modifier | modifier le code]
Expérience de pensée[modifier | modifier le code]
Considérons un fluide au repos. On délimite, par la pensée, un certain volume de forme quelconque au sein de ce fluide. Ce volume est lui aussi au repos : malgré son poids, ce volume ne tombe pas. Cela signifie donc que son poids est rigoureusement compensé par une force opposée, qui le maintient sur place, et qui provient du fluide extérieur. On remplace maintenant, toujours par la pensée, ce volume par un corps quelconque. Comme la force qui maintenait le fluide en équilibre est une force de pression agissant à la surface du volume, il est possible de supposer que cette même force s'applique encore au corps immergé : elle est toujours opposée au poids de fluide déplacé. C'est la poussée d'Archimède. Le fait que les champs de force soient identiques pour le fluide homogène au repos et pour le corps immergé dans le fluide au repos est appelé « théorème de solidification ».
Idée de la démonstration[modifier | modifier le code]
Supposons un cube d'arête a entièrement immergé dans un liquide, sa face du haut étant horizontale et située à une profondeur z1 > 0 (le sens positif est vers le bas). On notera le vecteur unitaire dirigé selon l'axe des z croissants (donc orienté vers le bas).
Dans le cas d'un liquide incompressible au repos soumis à un champ de pesanteur uniforme, la pression absolue p à une profondeur z vaut :
- où :
- p0 est la pression atmosphérique ;
- ph(z) est la pression hydrostatique à la profondeur z.
On considère une colonne de liquide, assimilable à un pavé droit de hauteur variable z et dont la surface de la base est constante et vaut A. À une profondeur z, la pression hydrostatique correspond à la norme P du poids de la colonne de liquide, divisé par la base A de la colonne de liquide : p(z) = P/A.
Or l'expression du poids de la colonne de liquide est :
- où :
- m est la masse de la colonne ;
- z∙A est son volume ;
- ρ est la masse volumique (supposée uniforme) du liquide ;
- g est l'accélération de la pesanteur.
On obtient donc, en utilisant la formule p(z) = P/A :
- .
La pression absolue vaut donc
- .
Par symétrie, les forces de pression exercées sur les quatre faces latérales du cube s'annulent deux à deux.
La force , exercée par le liquide sur la face supérieure (d'aire A = a2) du cube, est dirigée de haut en bas et vaut :
- .
La force dirigée du bas vers le haut, exercée par le liquide sur la face inférieure (d'aire A = a2) du cube, qui est située à la profondeur z2 = z1 + a, vaut :
- .
La résultante des forces de pression vaut donc :
- où :
- V = a 3 est le volume du cube, c'est-à-dire en l'occurrence le volume immergé ;
- mf est la masse du fluide contenu dans un volume V.
La force résultante est donc bien égale à l'opposé du poids du volume de liquide déplacé. Cette force étant négative, elle est bien orientée verticalement du bas vers le haut.
Il est possible de généraliser la démonstration précédente à un volume de forme quelconque. Il suffit de décomposer la surface bordant le volume en une infinité d'éléments infinitésimaux dS supposés plans, puis de faire la somme, à l'aide d'un calcul d'intégrales, de toutes les forces infinitésimales exercées sur chaque élément de surface.
Démonstration plus générale[modifier | modifier le code]
On peut déduire le théorème d'Archimède de celui du gradient[3] : supposons un volume quelconque V, délimité par une surface fermée S, plongé entièrement dans un fluide de masse volumique ρ soumis à un champ de pesanteur , non nécessairement uniforme.
Par définition de la pression p, la résultante des forces de pression exercées sur le volume est :
- où :
- est un élément infinitésimal de la surface considérée, orienté par convention de l'intérieur vers l'extérieur de cette surface ;
- p est la pression.
Par le théorème du gradient puis la loi fondamentale de l'hydrostatique, cette expression devient :
qui est l'opposé du poids du volume de fluide déplacé.
Applications[modifier | modifier le code]
Exemple d'un solide entièrement immergé[modifier | modifier le code]

Immergeons entièrement un solide de volume V, de masse m et de masse volumique ρ dans un fluide de masse volumique ρf uniforme, puis relâchons-le à partir du repos. Au départ, la vitesse étant nulle, deux forces seulement agissent sur le solide : son poids Fp (vers le bas) et la poussée d'Archimède Fa (vers le haut).
- Fp = ρ V g
- Fa = ρf V g
- Fp / Fa = ρ / ρf
Le rapport des masses volumiques est en l'occurrence équivalent à celui des densités :
- si la densité du solide est supérieure à celle du fluide, alors Fp > Fa et le solide coule ;
- si la densité du solide est égale à celle du fluide, alors Fp = Fa et le solide demeure immobile ; il est en équilibre neutre ou indifférent ;
- si la densité du solide est inférieure à celle du fluide, alors Fp < Fa et le solide remonte vers la surface.
Dans les deux cas où le solide n'est pas en équilibre, son mouvement ultérieur est déterminé par trois forces : son poids, la poussée d'Archimède (opposée au poids) et une force de frottement visqueux Ff (opposée à la vitesse).
Selon la deuxième loi du mouvement de Newton, on a alors :
- Fp – Fa ± Ff = m a (le sens positif est vers le bas)
où a est l'accélération du solide.
Comme la force de frottement visqueux n'est pas constante, mais qu'elle augmente avec la vitesse, l'accélération diminue graduellement, de sorte que le solide atteint[4] plus ou moins rapidement une vitesse limite, lorsque la résultante des forces est nulle.
Exemple d'un solide flottant à la surface d'un liquide[modifier | modifier le code]

Considérons un solide de volume V et de masse volumique ρS flottant à la surface d'un liquide de masse volumique ρL. Si le solide flotte, c'est que son poids est équilibré par la poussée d'Archimède :
- Fa = Fp .
La poussée d'Archimède étant égale (en valeur absolue) au poids du volume de liquide déplacé (égal au volume V i immergé), on peut écrire :
- ρL V i g = ρS V g — (1).
Le volume immergé vaut donc :
- V i = ( ρS / ρL ) V — (2).
Puisque V > V i, il s'ensuit que ρS < ρL .
Application au cas d'un iceberg[modifier | modifier le code]
Considérons un morceau de glace pure à 0 °C flottant dans de l'eau de mer. Soit ρS = 0,917 g/cm3 et ρL = 1,025 g/cm3 (on aurait ρL = 1,000 g/cm3 pour de l'eau pure à 3,98 °C). Le rapport ρSρL (c’est-à-dire la densité relative) est égal à 0,895, si bien que le volume immergé V i représente près de 90 % du volume total V de l'iceberg.
Un glaçon qui fond dans un verre[modifier | modifier le code]

Il est facile de vérifier que la fonte d'un morceau de glace pure flottant sur de l'eau pure se produit sans changement de niveau de l'eau. Le volume de glace immergé correspond en effet au volume d'eau liquide nécessaire pour égaler le poids du glaçon (Eq. 1). En fondant, le glaçon produit (par conservation de la masse) exactement ce volume d'eau, qui « bouche le trou laissé par la disparition de la glace solide ». Le niveau de l'eau reste le même. Sur la figure ci-contre, le volume délimité en pointillé est, dans le verre de gauche, le volume de glace immergée, et, dans le verre de droite, le volume d'eau liquide produit par la fonte du glaçon.
On peut également faire le calcul suivant : si on considère, par exemple, un glaçon de 1 cm3 et de masse volumique 0,917 g·cm−3 (qui contient donc 0,917 g d'eau), le volume immergé est 0,917 cm3 (Eq. 2) (comme pour un iceberg, la majeure partie est sous l'eau). Lorsque le glaçon aura fondu, ce 0,917 g d'eau qui aura désormais une masse volumique de 1 g·cm−3 occupera exactement le volume qu'occupait la partie immergée du glaçon.
Autres illustrations de la poussée d'Archimède dans l'eau[modifier | modifier le code]


- Pour vérifier le principe d'Archimède par l'expérience, on se sert d'un cylindre plein en cuivre, qui remplit exactement un vase cylindrique creux du même métal. On pèse le tout dans l'air ; après avoir ôté le cylindre plein du cylindre creux, on accroche le premier au-dessous du second et on le fait plonger entièrement dans l'eau. Ainsi disposé le système a perdu de son poids et la balance n'est plus en équilibre. Mais si l'on remplit d'eau le cylindre creux, l'équilibre se rétablit ce qui prouve que la différence entre la première et la seconde pesée était précisément le poids d'un volume d'eau égal à celui du cylindre immergé.
- Le corps humain étant à peu près de même densité que l'eau, il se trouvera proche d'un état de flottabilité indifférenciée, c'est-à-dire qu'il ne flotte ni ne coule. Il lui est alors facile en faisant varier la quantité d'air dans ses poumons - et de cette manière varier la densité du corps dans son entièreté - (et néanmoins quelques mouvements des bras et des jambes) de se maintenir à flot ou de plonger. Un plongeur se met à « couler » vers −12 m dans l'Atlantique ou la Méditerranée car sa densité augmente avec la profondeur (à cause de la compression croissante, particulièrement des bulles contenues dans le néoprène de sa combinaison : sa masse ne change pas mais son volume diminue) jusqu'à atteindre et dépasser celle du milieu ambiant.
- L'eau douce ayant une masse volumique plus faible que l'eau salée, la poussée d'Archimède est plus forte dans la mer Morte (mer la plus salée du monde) que dans un lac. Il est donc plus facile d'y flotter.
- La vessie natatoire des poissons osseux qui leur permet d'améliorer leur flottabilité n'est pas sans analogie avec les poumons. On a longtemps pensé qu'au cours de l'évolution de ces deux organes homologues, la vessie natatoire de certains poissons Sarcoptérygiens a abouti à la formation des poumons primitifs dont les Dipneustes et les Tétrapodes ont hérité. Plusieurs biologistes et paléontologues remettent en cause cette version et avancent que ce serait en fait les poumons qui auraient évolué en une vessie natatoire. Le requin qui est privé de cet organe est obligé pour ne pas couler de nager sans arrêt.
- Les sous-marins contrôlent de manière semblable leur flottaison en utilisant des caisses de réglage, dont le niveau est ajusté pour équilibrer le poids du sous-marin en plongée en fonction de l'immersion, de la salinité et de la température de l'eau de mer. Dans un sous-marin, le terme de ballast est réservé pour d'autres caisses, non réglables, qui sont entièrement remplis d'air pour maintenir le sous-marin en surface, et entièrement remplis d'eau quand le sous-marin est en plongée[6].
- Cette technique est mise à profit également par les navires. Pour maintenir un niveau de flottaison (tirant d'eau) constant et assurer une meilleure stabilité, les navires sont pourvus de ballast qu'ils peuvent remplir ou vider suivant leur cargaison ou la salinité de l'eau dans laquelle ils naviguent (Voir aussi carène et déplacement (navire)). Les navires sont en charge ou sur lest et leur poids contrecarré par la poussée d'Archimède qui va également varier.
- Les spationautes s'entraînent aux exercices dans l'espace dans des piscines aménagées spécialement - Laboratoire de flottabilité neutre - où, grâce à la poussée d'Archimède qui équilibre leur poids, ils peuvent connaître un état qui s'« apparente » à l'impesanteur.
- Le ludion est un montage de physique (ou un jouet) illustrant la forte compressibilité de l'air par rapport à celle de l'eau.
- Le thermomètre de Galilée.
- L'hydromètre qui permet la mesure de la masse volumique d'un liquide.
Autres illustrations de la poussée d'Archimède dans l'air[modifier | modifier le code]
- Ce qui vient d'être dit s'applique à un fluide pesant quelconque. Pour connaître le poids d'un corps il faudrait le peser dans le vide. Si l'on savait combien il pèse dans l'air ou dans tout autre fluide il faudrait ajouter à ce poids celui d'un volume égal de ce fluide pour avoir le véritable poids du corps.
- La poussée d'Archimède s'exerçant pour les gaz, l'homme, pour s'élever dans les airs, a premièrement pensé à se doter d'un énorme ballon rempli d'un gaz plus léger que l'air (air chauffé ou gaz), variante en quelque sorte de la vessie natatoire des poissons[7]. Les idées de ce genre qui commençaient à se faire jour dès le milieu du XVIIe siècle et anticipée par les jésuites Francesco Lana de Terzi (1631-1687), Bartolomeu Lourenço de Gusmão (1685-1724) et Joseph Galien (en) (1699-1762), sont complètement réalisées par les frères Montgolfier et Jacques Charles en 1782 et 1783.
Point d'application[modifier | modifier le code]
Tout se passe comme si la poussée d'Archimède s'appliquait au centre de carène, c'est-à-dire au centre de gravité du volume de fluide déplacé[5].
Cette caractéristique est importante pour le calcul de la stabilité d'un sous-marin en plongée ou d'un aérostat : sous peine de voir ces engins se retourner, il est nécessaire que leur centre de carène soit situé au-dessus de leur centre de gravité.
Pour ce qui est d'un navire, en revanche, le centre de carène est souvent situé au-dessous du centre de gravité afin d'éviter des moments de redressement trop importants. Cependant, lorsque l'inclinaison du navire change (roulis), le centre de carène se déplace latéralement plus que le centre de gravité, ce qui génère un couple qui tend à ramener le navire à son inclinaison d'origine. La stabilité est alors assurée par la position du métacentre, qui est le point d'application des variations de la poussée. Ce métacentre doit se trouver au-dessus du centre de gravité.
De façon anecdotique, on peut remarquer que les concepteurs de sous-marins doivent s'assurer simultanément de deux types d'équilibres pour leurs engins : l'équilibre en plongée et l'équilibre en surface.
L'expérience d'Archimède, histoire et légende[modifier | modifier le code]

Le Traité des corps flottants, où Archimède énonce les lois de la statique des fluides - et des conditions d'équilibre des corps solides immergés dans un fluide ou flottant sur lui - est probablement la plus connue des œuvres d'Archimède, car tout le monde a présent à l'esprit l'anecdote rapportée par Vitruve suivant laquelle Archimède aurait eu l'intuition du principe fondamental de l'hydrostatique en prenant un bain[8] :
Archimède, savant grec qui vécut à Syracuse, en Sicile de 287 av. J.-C. à 212 av. J.-C., est connu pour ses multiples travaux scientifiques, théoriques ou pratiques, que ce soit en mathématique ou en physique. Le Traité des corps flottants qui étudie avec rigueur l'immersion d'un corps, solide ou fluide, dans un fluide de densité inférieure, égale ou supérieure, jette les bases de la branche de mécanique des fluides, ce que l'on nommera plus tard « hydrostatique ». Dans cet ouvrage se trouve le théorème qui portera le nom du savant[9], qui ne sera complètement démontré qu'au XVIe siècle.
Le Traité des corps flottants contient d'autres propositions relatives à la poussée d'Archimède[9] :
- Proposition III : un solide de même volume et de même poids (en fait de même masse volumique) que le liquide dans lequel il est abandonné y enfoncera de façon à n’émerger nullement au-dessus de la surface, mais à ne pas descendre plus bas ;
- Proposition IV : aucun corps plus léger que le liquide où il est abandonné ne sera complètement immergé, mais restera en partie au-dessus de la surface du liquide ;
- Proposition V : un solide plus léger que le liquide dans lequel on l’abandonne s'y enfonce de telle façon qu’un volume de liquide égal à la partie immergée a le même poids que le solide entier ;
- Proposition VI : lorsqu’un corps est plus léger que le liquide où on l’enfonce et remonte à la surface, la force qui pousse en haut ce corps a pour mesure la quantité dont le poids d’un égal volume de liquide surpasse le poids même du corps ;
- Proposition VII : un corps plus lourd que le liquide où on l’abandonne descendra au fond et son poids, dans le liquide, diminuera d’une quantité mesurée par ce que pèse un volume de liquide égal à celui du corps.
La couronne du roi Hiéron II[modifier | modifier le code]

Vitruve[10] rapporte que le roi Hiéron II de Syracuse (306-214) aurait demandé à son jeune ami et conseiller scientifique Archimède (âgé alors de 22 ans) de vérifier si une couronne d'or, qu'il s'était fait confectionner comme offrande à Zeus, était totalement en or ou si l'artisan y avait mis de l'argent. La vérification avait bien sûr pour contrainte de ne pas détériorer la couronne. La forme de celle-ci était en outre trop complexe pour effectuer un calcul du volume de l'ornement. Archimède aurait trouvé le moyen de vérifier si la couronne était vraiment en or, alors qu'il était au bain public, en observant comment des objets y flottaient. Il serait alors sorti dans la rue entièrement nu en s'écriant « Eurêka ! » (j'ai trouvé !), formule depuis lors devenue célèbre.
La constatation qu'Archimède fait au bain public est que, pour un même volume donné, les corps n'ont pas le même poids, c'est-à-dire ont une masse par unité de volume différente. On parle de nos jours de masse volumique. L'argent (masse volumique 10 500 kg m−3) est moins dense que l'or (masse volumique 19 300 kg m−3), il a donc une masse volumique plus faible : pour obtenir la même masse, il faut une plus grande quantité d'argent que d'or. Si l'artisan a caché de l'argent dans la couronne du roi, Archimède déduit que la couronne doit être plus volumineuse que si elle avait été faite exclusivement en or. Ainsi fut démasquée la supercherie du joaillier.
La solution au problème[modifier | modifier le code]
Afin de répondre à la question du roi Hiéron, Archimède a donc pu comparer les volumes d'eau déplacés par la couronne et une quantité d'or de masse identique. Si les deux déplacent le même volume d'eau, leur masse volumique est alors égale et on peut en conclure que les deux sont composés du même métal. Pour réaliser l'expérience, on peut imaginer plonger la masse d'or dans un récipient rempli à ras-bord (et muni d'un bec verseur pour mieux observer la chose). Une certaine quantité d'eau débordera alors du récipient (on peut la recueillir pour la mesurer). Ensuite, on retire l'or et on le remplace par la couronne à étudier. Si la couronne est bien totalement en or, alors l'eau ne débordera pas. En revanche, si sa densité est plus faible et donc son volume plus important pour la même masse, de l'eau supplémentaire débordera.
Le volume d'eau déplacé dépendra de la proportion d'argent dans l'or ; l'or étant approximativement deux fois plus dense que l'argent, remplacer 10 % en masse d'or par de l'argent conduit à une hausse de volume de 10 %[11]. Mais du fait de la forte masse volumique de l'or, son volume est très faible : le volume d'une couronne de 1 kg d'or n'est que d'un peu plus de 50 cm3 et substituer 10 % d'or par de l'argent ne produit une différence que d'environ de 4,34 cm3 (le volume d'eau d'une petite cuillère)
La méthode ainsi décrite par Vitruve présente deux inconvénients. Le premier est qu'elle ne fait ici intervenir en rien le principe d'Archimède. Le second problème est qu'avec des conditions réalistes, en raison de la densité de l'or et du volume faible de la couronne, le volume d'eau déplacée est très faible et sa mesure est perturbée par l'eau qui peut être perdue dans les différentes opérations. Il est donc peu probable qu'Archimède ait pu tirer des conclusions significatives à partir d'une telle expérience.
Une méthode plus réaliste est la suivante. On équilibre une balance avec la couronne d'un côté et de l'or pur de l'autre, dont les masses sont égales. Ensuite, on immerge complètement les objets pesés (pour s'affranchir de l'influence des plateaux de la balance, on peut s'assurer que ceux-ci sont bien strictement identiques, ou, mieux, les supprimer en les remplaçant par un fil fin et de densité proche de celle de l'eau). Si la couronne n'est pas en or pur, elle est de volume un peu plus grand, donc elle produit une force d'Archimède vers le haut un peu plus importante que la même masse d'or pur et l'équilibre initial de la balance est rompu. Là encore, la différence de poids est faible ; dans les conditions imaginées plus haut elle correspond au poids de 5 cm3 d'eau, soit 5 g. Il faut donc une balance capable de détecter une telle variation, ce qui est difficile, mais pas irréaliste.
L'appareil a effectivement été réalisé sous le nom de balance hydrostatique.
Postérité[modifier | modifier le code]
L'anecdote est perpétuée par des titres comme La Baignoire d'Archimède. Petite mythologie de la science de Sven Ortoli et Nicolas Witkowski (1998), ou encore La baignoire d'archimède - anthologie poétique de l'Obériou de Henri Abril (2012).
Notes et références[modifier | modifier le code]
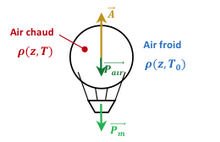
- Les différentes forces qui agissent sur la montgolfière sont le poids de la montgolfière, le poids de l'air dans le ballon et la poussée d'Archimède.
- Joseph Kane et Morton Sternheim, Physique: plus de 1900 problèmes et exercices, plus de 800 solutions, Masson, coll. « Enseignement de la physique », (ISBN 978-2-225-83137-9), p. 294
- (en) James Stewart (en), Calculus : Concepts and Contexts, Cengage Learning, , 4e éd. (lire en ligne), p. 972,ex. 32.
- Mathématiquement, le solide tend de façon asymptotique vers une vitesse limite. En pratique, on considère la vitesse limite atteinte quand l'accélération n'est plus perceptible.
- Comme le poids, la poussée d'Archimède n'est pas une force unique, mais une résultante. Elle n'a donc pas à proprement parler de point d'application, mais plus rigoureusement, il s'agit d'un glisseur d'axe passant par le centre de carène et de direction verticale.
- Ministère de la défense, « Plongée et retour en surface d’un sous-marin », sur defense.gouv.fr
- Jacques H. Corriol. La plongée en apnée: physiologie, médecine, prévention. Elsevier Masson, 9 févr. 2006
- Gabriel Lamé. Propriétés générales des corps. Théorie physique de la chaleur. Bachelier, 1840. Lire en ligne.
- Adrien Legrand, Le traité des corps flottants d’Archimède. Traduction nouvelle. J. Phys. Theor. Appl., 1891, 10 (1), p. 437-457 (lire en ligne).
- Vitruve, « De Architectura, Livre IX, chap.3, paragraphes 9–12 », Université de Chicago (consulté le )
- On enlève 10 % du volume en or, on ajoute deux fois 10 % = 20 % du volume en argent ; –10 % + 20 % = +10 % en volume
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Hydrostatique :
- Mécanique des fluides :
- L'expérience du ludion
- Pont d'Archimède
- Vis d'Archimède
- Axiome d'Archimède
- Force ascensionnelle
Liens externes[modifier | modifier le code]
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Archimède : histoire et physique

























