« Conduction thermique » : différence entre les versions
Mauvaise illustration pour ce phénomène seul, comme expliqué en Pdd |
Un peu de physique |
||
| Ligne 68 : | Ligne 68 : | ||
où A et B sont des constantes à fixer selon les conditions aux limites. |
où A et B sont des constantes à fixer selon les conditions aux limites. |
||
=== Échelle microscopique : l'équation de Boltzmann === |
|||
Dans les problèmes à l'échelle nanométrique tels qu'on les rencontre par exemple en [[microélectronique]] le [[libre parcours moyen]] des phonons n'est pas petit devant la taille de l'objet étudié et l'équation de diffusion de la chaleur n'est plus valide. Ce problème a été résolu par [[Rudolf Peierls]] en 1929<ref>{{article|langue=de|auteur=[[Rudolf Peierls|R. E. Peierls]]|titre= Zur kinetischen Theorie der Wärmeleitung in Kristallen|périodique= [[Annalen der Physik]]|volume=3|pages=1055–1101|année=1929}}</ref> en donnant une description microscopique du phénomène par l'intermédiaire d'une [[équation de Boltzmann]] pour l'énergie dE<sub>ν</sub> transférée par les phonons considérés comme un gaz, à l'instar du [[gaz de photons]]. Cette énergie est ramenée à l'unité d'aire traversée dS, à l'intervalle de fréquence considéré dν, à l'angle solide élémentaire considéré d'''Ω''' et à l'intervalle de temps temps dt pour donner une intensité I<sub>ν</sub> |
|||
::<math>\mathrm{d}E_\nu=I_\nu\mathrm{d}S\mathrm{d}\nu\mathrm{d}\Omega\mathrm{d}t</math> |
|||
Cette quantité est l'analogue de la [[Luminance énergétique|luminance]] spectrale pour le rayonnement. Elle obéit à l'[[équation de Boltzmann]] que l'on donne ici en une dimension d'espace et dans le cas stationnaire<ref>{{ouvrage|langue=en|auteur1=Ingo Müller|auteur2=Tommaso Ruggeri|titre=Rational Extended Thermodynamics|éditeur=[[Springer Science+Business Media|Springer]]|collection=Springer Tracts in Natural Philosophy|volume=37|année=1998|ISBN=978-1-4612-7460-5}}</ref> |
|||
::<math>\frac{\mathrm{d}I_\nu(x,\mu)}{\mathrm{d}\tau}=G_\nu(x)-I_\nu(x,\mu)</math> |
|||
Pour cela : |
|||
* on a introduit la quantité  <math>\tau=\kappa x</math>  où κ est le coefficient d'absorption spectral du milieu supposé indépendant de ν. Cette quantité est l'inverse du [[libre parcours moyen]] l = 1 / τ, typiquement quelques dizaines de nm à température ambiante; |
|||
* on a supposé que la dépendance angulaire était de révolution, caractérisée par μ = cos θ ; |
|||
* on a négligé les termes de [[Diffusion des ondes|diffusion]] pouvant résulter de défauts cristallins ou de processus [[umklapp]]. |
|||
G<sub>ν</sub> est le terme de création qui résulte de la création de phonons par agitation thermique. |
|||
Dans le cas où l'équilibre thermodynamique est atteint ce terme est donné par la [[loi de Planck]] (les phonons sont des [[bosons]] tout comme les photons, ils obéissent donc à la [[statistique de Bose-Einstein]]) |
|||
::<math>B_\nu=\frac{2h\nu^3}{c_m^2}\frac{1}{\exp\left(\frac{h\nu}{kT_m}\right)-1}\,,\qquad B_m=\int_0^\infty B_\nu\mathrm{d}\nu=\frac{\sigma T_m^4}{\pi}</math> |
|||
où |
|||
{| |
|||
|- |
|||
| <math>T_m</math> ||   température de vibration unique pour tous les degrés de liberté du réseau cristallin dilatation, torsio, flexion), |
|||
|- |
|||
| <math>h</math> ||   [[constante de Planck]], |
|||
|- |
|||
| <math>k</math> ||   [[constante de Boltzmann]], |
|||
|- |
|||
| <math>\sigma</math> ||   [[constante de Stefan-Boltzmann]], |
|||
|- |
|||
| <math>c_m</math> ||   vitesse de groupe pour la propagation (typiquement quelques milliers de m / s). C'est la moyenne des vitesses longitudinale et transversale, quelquefois nommée '''vitesse de Debye'''. |
|||
|} |
|||
Dans l'hypothèse de l'équilibre thermodynamique du milieu on peut écrire une équation pour l'intensité qui est identique à celle du [[transfert radiatif]]. on obtient une équation pour l'intensité intégrée en fréquence   <math>I_m=\int_0^\infty I_\nu\mathrm{d}\nu</math> |
|||
::<math>\frac{\mathrm{d}I_m(x,\mu)}{\mathrm{d}\tau}=B_m(T_m(x))-I_m(x,\mu)</math> |
|||
=== Lien avec l'échelle macroscopique === |
|||
Introduisons les premiers moments de I<sub>m</sub> : |
|||
{| |
|||
|- |
|||
| l'énergie ||   <math>E_m=2\pi\int_{-1}^1I_m\mathrm{d}\mu=\int \rho C_V\mathrm{d}T</math> |
|||
|- |
|||
| le flux de chaleur ||   <math>\Phi_m=2\pi\int_{-1}^1\mu I_m\mathrm{d}\mu</math> |
|||
|} |
|||
où ρ est la masse volumique et C<sub>V</sub> la [[capacité thermique massique]]. |
|||
Lorsque : |
|||
* le libre parcours moyen est petit devant la dimension du domaine ou tout autre quantité s caractérisant la solution soit  <math>l<<\frac{s}{\left|\frac{\partial s}{\partial x}\right|}</math> , |
|||
* le temps caractéristique  <math>t_m=\frac{1}{\kappa c_m}</math>  est petit devant toute variation temporelle dans le domaine  <math>t_m <<\frac{s}{\left|\frac{\partial s}{\partial t}\right|}</math> , |
|||
[[Transfert radiatif#Approximations|diverses méthodes]]<ref name="Modest">{{ouvrage|langue=en|nom= Michael M. Modest|titre=Radiative Heat Transfer|éditeur= [[Academic Press]]|année= 2003 |ISBN= 0-12-503163-7}}</ref> permettent d'obtenir une équation de diffusion reliant ces quantités sous la forme : |
|||
::<math>\Phi_m=-\frac{c_m}{3}\frac{\partial E_m}{\partial x}=-\frac{c_m}{3\kappa}\frac{\mathrm{d}E_m}{\mathrm{d}T}\frac{\partial T}{\partial x}=-\frac{c_m\rho \,C_V}{3\kappa}\frac{\mathrm{d}T}{\mathrm{d}x}</math> |
|||
On reconnait la [[loi de Fourier]] avec une conductivité thermique valant |
|||
::<math>\lambda=\frac{c_m\rho \,C_V}{3\kappa}</math> |
|||
{{Démonstration| |
|||
Comme en [[Transfert radiatif#Approximations|transfert radiatif]] on peut réduire l'équation de Boltzmann au système suivant |
|||
:<math> |
|||
\begin{array}{rcl} |
|||
\frac{\partial E_m}{\partial t} + \frac{\partial \mathbf \Phi_m}{\partial x} & = & \kappa \left(4\pi B_m- c_mE_m\right) \\[0.6em] |
|||
\frac{\partial \mathbf \Phi_m}{\partial t} + c_m^2\frac{\partial \mathbf (E_m \mathsf{D}_m)}{\partial x} & = & -c_m\kappa \mathbf \Phi_m |
|||
\end{array} |
|||
</math> |
|||
On suppose le tenseur  <math>\textstyle\mathsf{D}_m </math>  isotrope :  <math>\textstyle\mathsf{D}_\nu =\frac{1}{3}\mathsf{I}</math>  : c'est la méthode d'[[Arthur Eddington|Eddington]] ou [[Méthode PN|méthode P<sub>1</sub>]]. |
|||
On obtient alors |
|||
:<math>c_m^2\frac{\partial \mathbf (E_m \mathsf{D}_m)}{\partial x}=\frac{c_m^2}{3}\frac{\partial E_m }{\partial x}</math> |
|||
Dans l'hypothèse d'un flux stationnaire, la seconde équation du système ci-dessus s'écrit |
|||
:<math>\Phi_m=-\frac{c_m}{3\kappa}\frac{\partial E_m }{\partial x}</math> |
|||
}} |
|||
La conductivité thermique est proportionnelle à la vitesse de propagation, à la capacité thermique massique et au libre parcours moyen dans le milieu. |
|||
Par suite le coefficient de diffusion thermique  <math>D=\frac{\lambda}{\rho C_V}=\frac{c_m}{3\kappa}</math>  est proportionnelle à la vitesse de propagation et au libre parcours moyen. |
|||
L'équation de la chaleur obtenue avec cette approximation diffusive est une [[Équation aux dérivées partielles parabolique|équation parabolique]] pour laquelle la vitesse de propagation de l'information est infinie. |
|||
=== Échelles de temps courts : l'équation de Cattaneo-Vernotte === |
|||
Dans certains cas l'hypothèse de quasi-stationnarité du flux n'est plus valide : par exemple si on utilise une source de chaleur ultra-brève comme une impulsion laser pour chauffer un échantillon. |
|||
Si on conserve le terme temporel sur le flux (voir encadré précédent) on obtient : |
|||
::<math>\Phi_m+t_m\frac{\partial \Phi_m}{\partial t}=-\frac{c_m}{3\kappa}\frac{\partial E_m}{\partial x}=-\lambda\frac{\mathrm{d}T}{\mathrm{d}x}\,,\qquad t_m=\frac{1}{\kappa c_m}</math> |
|||
Cette expression du flux comportant un terme de relaxation de l'oscillation des phonons est appelée '''équation de Cattaneo-Vernotte''' d'après [[Carlo Cattaneo (mathématicien)|Carlo Cattaneo]]<ref>{{article|langue=it|auteur=[[Carlo Cattaneo (mathématicien)|Carlo Cattaneo]]|titre=Sulla conduzione del calore|périodique= |
|||
Atti del Seminario Matematico e Fisico dell' Universita di Modena e Reggio Emilia |volume= 3 |pages=83–101|année=1948}}</ref> et Pierre Vernotte<ref>{{article|auteur=P. Vernotte|titre=Les paradoxes de la théorie continue de l'équation de la chaleur|périodique=[[Comptes rendus hebdomadaires des séances de l'Académie des sciences|Comptes-rendus de l'Académie des sciences]]| volume=246|pages= 3154-3155|année=1958 1958}}</ref>. Le système auquel elle conduit est du type [[équations des télégraphistes]]. On notera que dans ce système d'[[équation aux dérivées partielles hyperbolique]] la vitesse de propagation de l'information est  <math>\frac{c_m}{\sqrt 3}</math>  et non c<sub>m</sub>. |
|||
=== Échelle nanoscopique : le quantum de chaleur === |
|||
On considère un [[guide d'onde]] virtuel de taille nanoscopique. [[Rolf Landauer]] a montré<ref>{{ouvrage|langue=en|auteur=Yoseph Imry|titre=Introduction to Mesoscopic Physics|éditeur=[[Oxford University Press]]|année=2002|ISBN=0-19-850738-0|url=https://books.google.fr/books?id=ZyjW37iGhaQC&pg=PA221&lpg=PA221&dq=landauer+r&source=bl&ots=Wy5THlhZ9B&sig=T1O4SzdL3qKXnUbm0QNKN1HCWRY&hl=fr&sa=X&ved=0ahUKEwiHnP2J4d_bAhVJdcAKHREcCe0Q6AEIfzAO#v=onepage&q=landauer%20r&f=false}}</ref> que le flux de chaleur pour le mode de propagation α entre un milieu 1 et un milieu 2 à l'équilibre thermodynamique est |
|||
::<math>\Phi_\alpha=\int_0^\infty \hbar \omega_\alpha(k)c_m(k)(n_2-n_1)\mathcal{T}_\alpha\frac{\mathrm{d}k}{2\pi}</math> |
|||
où |
|||
{| |
|||
|- |
|||
| <math>k</math> || [[nombre d'onde]] ; |
|||
|- |
|||
| <math>\omega_\alpha(k)</math> || [[Phonon#Comportement et propriétés des phonons|relation de dispersion]] ; |
|||
|- |
|||
| <math>n=\left(e^{\frac{\hbar \omega}{kT}}-1\right)^{-1}</math> || [[Fonction de partition|nombre d'occupation]] de la [[statistique de Bose-Einstein]] ; |
|||
|- |
|||
| <math>\mathcal{T}_\alpha</math> || facteur de transmission. |
|||
|} |
|||
Le guide est limité par deux surfaces permettant un échange parfait : <math>\mathcal{T}_\alpha=1</math>. À ses extrémités on applique deux milieux avec une différence de température  <math>\Delta T=T_2-T_1</math>  et on considère la limite  <math>\Delta T \to 0</math> . On suppose que ces températures sont suffisamment faibles pour avoir le droit de ne prendre en compte que le nombre d'onde k = 0 pour chaque mode. |
|||
Avec ces hypothèses on montre que le [[quantum]] de conductance par mode est<ref>{{article|langue=en|auteur=[[John Pendry|J. B. Pendry]]|titre=Quantum Limits to the Flow of Information and Entropy|périodique=Journal of Physics A: Mathematical and General|volume=16|numéro=10|année=1983|pages=2161-2171|url=http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.485.9140&rep=rep1&type=pdf}}</ref> |
|||
::<math>q_\alpha=\frac{\Phi_\alpha}{\Delta T}=\frac{\pi k^2}{3h}\frac{T_1+T_2}{2}</math> |
|||
Cette valeur a été mesurée expérimentalement<ref>{{article|langue=en|auteur1=K. Schwab|auteur2=E. A. Enriksen|auteur3=J. M. Worlock|auteur4=M. L. Roukes|titre=Measurement of the Quantum of Thermal Conductance|périodique=[[Nature (revue)|Letters to Nature]]|volume=404|année=2000|pages=974-977|url=https://www.its.caltech.edu/~nano/publications/papers/Nature404-974.pdf}}</ref>. |
|||
== Conduction en régime stationnaire == |
== Conduction en régime stationnaire == |
||
Version du 27 juin 2018 à 15:25
La conduction thermique (ou diffusion thermique) est un mode de transfert thermique provoqué par une différence de température entre deux régions d'un même milieu, ou entre deux milieux en contact, et se réalisant sans déplacement global de matière[1] (à l'échelle macroscopique) par opposition à la convection qui est un autre transfert thermique. Elle peut s'interpréter comme la transmission de proche en proche de l'agitation thermique : un atome (ou une molécule) cède une partie de son énergie cinétique à l'atome voisin.
La conduction thermique est un processus de transport de l'énergie interne lié à l'agitation moléculaire et dû à une hétérogénéité du milieu à l'échelle macroscopique[2]. C'est un phénomène irréversible analogue au phénomène de diffusion[2]. Dans les fluides (liquides et gaz) ce transport d'énergie résulte au niveau microscopique de l'anisotropie de la fonction de distribution des vitesses. Dans les solides, la conduction thermique est assurée conjointement par les électrons de conduction et par les vibrations du réseau cristallin (phonons)[3].
Phénomènes physiques

La conduction thermique est le déplacement de l'énergie thermique des parties chaudes d'un système[4] vers les parties froides. Lorsque l'énergie diffuse dans un système, les différences de température décroissent et l'entropie croît.
Dans le cas le plus simple des gaz, la diffusion de l'énergie thermique intervient quand, au cours de son mouvement de translation, une particule cède une partie de sa quantité de mouvement à d'autres particules lors de collisions.
Dans les solides, le mouvement de translation prend la forme de phonons (voir la figure). Les phonons sont des quantités élémentaires (quantifiées) d'énergie de vibration se déplaçant dans un solide à la vitesse du son propre à la substance. La manière dont les phonons interagissent dans le solide détermine leurs propriétés, telles que la diffusion thermique. Les isolants électriques, par exemple, ont généralement une conductivité thermique faible[5] et ces solides sont considérés comme des isolateurs thermiques (comme le verre, les matières plastiques, le caoutchouc, les céramiques et la pierre). Ceci est dû au fait que dans les solides, les atomes et molécules ne sont pas libres de se déplacer.
Les métaux, toutefois, présentent une forte conductivité thermique. En effet, leur structure permet une diffusion de l'énergie cinétique par les électrons de conduction, légers et extrêmement mobiles. C'est pourquoi il existe, dans les métaux, une corrélation presque parfaite entre la conductivité électrique et la conductivité thermique[6]. La conductivité électronique prédomine dans les métaux parce que les électrons sont délocalisés, c'est-à-dire qu'il ne sont pas liés à un atome et qu'ils se comportent comme un gaz quantique.
Généralités sur la modélisation
Loi de Fourier
La conduction thermique est un transfert thermique spontané d'une région de température élevée vers une région de température plus basse, et est décrite par la loi dite de Fourier établie mathématiquement par Jean-Baptiste Biot en 1804 puis expérimentalement par Fourier en 1822[7] : la densité de flux de chaleur est proportionnelle au gradient de température.
La constante de proportionnalité λ est nommée conductivité thermique du matériau. Elle est toujours positive. Avec les unités du Système international, la conductivité thermique λ s'exprime en watt par mètre-kelvin (W⋅m−1⋅K−1). La densité de flux de chaleur s'exprime en watt par mètre carré (W⋅m−2), la température T, en kelvin (K).
La loi de Fourier est une loi semi-empirique analogue à la loi de Fick pour la diffusion de particule ou la loi d'Ohm pour la conduction électrique (Ohm s'est d'ailleurs servi d'une analogie entre thermique et électricité pour construire sa théorie). Ces trois lois peuvent s'interpréter de la même façon : l'inhomogénéité d'un paramètre intensif (température, nombre de particules par unité de volume, potentiel électrique) provoque un phénomène de transport tendant à combler le déséquilibre (flux thermique, courant de diffusion, courant électrique).

Nous pouvons exprimer le transfert thermique selon Ox pendant un temps dt. On suppose que la quantité de chaleur traversant une surface d'aire dSx est proportionnelle à dSx, au temps de transfert dt et au taux de variation de la température T :
Le flux thermique à travers la surface élémentaire dSx est alors :
Nous pouvons en déduire la densité de flux dans la direction Ox :
Le même raisonnement dans chacune des directions de l'espace donne la loi de Fourier.
Équation de la chaleur
Un bilan d'énergie, et l'expression de la loi de Fourier conduit à l'équation générale de conduction de la chaleur dans un corps homogène : où :
- est la conductivité thermique du matériau en W⋅m−1⋅K−1.
- désigne le laplacien de la température,
- P est l'énergie produite au sein même du matériau en W⋅m−3. Elle est souvent nulle (cas des dépôts de chaleur en surface de murs, par exemple), mais l'on peut citer de nombreux cas où elle ne l'est pas ; citons parmi d'autres l'étude du transfert thermique par conduction au sein du combustible nucléaire, ou l'absorption de la lumière ou des micro-ondes au sein des matériaux semi-transparents...,
- ρ est la masse volumique du matériau en kg⋅m−3,
- et c est la chaleur spécifique massique du matériau en J⋅kg−1⋅K−1.
(établissement de l'équation de conduction de la chaleur)
Sous forme unidimensionnelle et dans le cas où P est nulle, on obtient :
En régime stationnaire, lorsque la température n'évolue plus avec le temps et si P est nul, elle se réduit à :
qui est une équation de Laplace. T est alors une fonction harmonique.
Dans le cas d'un régime permanent et unidimensionnel, l'équation précédente se réduit à :
dont la solution est :
où A et B sont des constantes à fixer selon les conditions aux limites.
Échelle microscopique : l'équation de Boltzmann
Dans les problèmes à l'échelle nanométrique tels qu'on les rencontre par exemple en microélectronique le libre parcours moyen des phonons n'est pas petit devant la taille de l'objet étudié et l'équation de diffusion de la chaleur n'est plus valide. Ce problème a été résolu par Rudolf Peierls en 1929[8] en donnant une description microscopique du phénomène par l'intermédiaire d'une équation de Boltzmann pour l'énergie dEν transférée par les phonons considérés comme un gaz, à l'instar du gaz de photons. Cette énergie est ramenée à l'unité d'aire traversée dS, à l'intervalle de fréquence considéré dν, à l'angle solide élémentaire considéré dΩ et à l'intervalle de temps temps dt pour donner une intensité Iν
Cette quantité est l'analogue de la luminance spectrale pour le rayonnement. Elle obéit à l'équation de Boltzmann que l'on donne ici en une dimension d'espace et dans le cas stationnaire[9]
Pour cela :
- on a introduit la quantité où κ est le coefficient d'absorption spectral du milieu supposé indépendant de ν. Cette quantité est l'inverse du libre parcours moyen l = 1 / τ, typiquement quelques dizaines de nm à température ambiante;
- on a supposé que la dépendance angulaire était de révolution, caractérisée par μ = cos θ ;
- on a négligé les termes de diffusion pouvant résulter de défauts cristallins ou de processus umklapp.
Gν est le terme de création qui résulte de la création de phonons par agitation thermique.
Dans le cas où l'équilibre thermodynamique est atteint ce terme est donné par la loi de Planck (les phonons sont des bosons tout comme les photons, ils obéissent donc à la statistique de Bose-Einstein)
où
| température de vibration unique pour tous les degrés de liberté du réseau cristallin dilatation, torsio, flexion), | |
| constante de Planck, | |
| constante de Boltzmann, | |
| constante de Stefan-Boltzmann, | |
| vitesse de groupe pour la propagation (typiquement quelques milliers de m / s). C'est la moyenne des vitesses longitudinale et transversale, quelquefois nommée vitesse de Debye. |
Dans l'hypothèse de l'équilibre thermodynamique du milieu on peut écrire une équation pour l'intensité qui est identique à celle du transfert radiatif. on obtient une équation pour l'intensité intégrée en fréquence
Lien avec l'échelle macroscopique
Introduisons les premiers moments de Im :
| l'énergie | |
| le flux de chaleur |
où ρ est la masse volumique et CV la capacité thermique massique.
Lorsque :
- le libre parcours moyen est petit devant la dimension du domaine ou tout autre quantité s caractérisant la solution soit ,
- le temps caractéristique est petit devant toute variation temporelle dans le domaine ,
diverses méthodes[10] permettent d'obtenir une équation de diffusion reliant ces quantités sous la forme :
On reconnait la loi de Fourier avec une conductivité thermique valant
La conductivité thermique est proportionnelle à la vitesse de propagation, à la capacité thermique massique et au libre parcours moyen dans le milieu.
Par suite le coefficient de diffusion thermique est proportionnelle à la vitesse de propagation et au libre parcours moyen.
L'équation de la chaleur obtenue avec cette approximation diffusive est une équation parabolique pour laquelle la vitesse de propagation de l'information est infinie.
Échelles de temps courts : l'équation de Cattaneo-Vernotte
Dans certains cas l'hypothèse de quasi-stationnarité du flux n'est plus valide : par exemple si on utilise une source de chaleur ultra-brève comme une impulsion laser pour chauffer un échantillon.
Si on conserve le terme temporel sur le flux (voir encadré précédent) on obtient :
Cette expression du flux comportant un terme de relaxation de l'oscillation des phonons est appelée équation de Cattaneo-Vernotte d'après Carlo Cattaneo[11] et Pierre Vernotte[12]. Le système auquel elle conduit est du type équations des télégraphistes. On notera que dans ce système d'équation aux dérivées partielles hyperbolique la vitesse de propagation de l'information est et non cm.
Échelle nanoscopique : le quantum de chaleur
On considère un guide d'onde virtuel de taille nanoscopique. Rolf Landauer a montré[13] que le flux de chaleur pour le mode de propagation α entre un milieu 1 et un milieu 2 à l'équilibre thermodynamique est
où
| nombre d'onde ; | |
| relation de dispersion ; | |
| nombre d'occupation de la statistique de Bose-Einstein ; | |
| facteur de transmission. |
Le guide est limité par deux surfaces permettant un échange parfait : . À ses extrémités on applique deux milieux avec une différence de température et on considère la limite . On suppose que ces températures sont suffisamment faibles pour avoir le droit de ne prendre en compte que le nombre d'onde k = 0 pour chaque mode.
Avec ces hypothèses on montre que le quantum de conductance par mode est[14]
Cette valeur a été mesurée expérimentalement[15].
Conduction en régime stationnaire
On définit un régime permanent (ou stationnaire) quand les températures ne dépendent pas du temps. La température ne dépend plus que de la disposition du point où l'on effectue la mesure et plus du temps. Pour toute la suite de ce chapitre, nous supposerons un régime permanent établi.
Surface plane simple
Le matériau est un milieu thermiquement conducteur limité par deux plans parallèles (cas d'un mur). Chaque plan a une température T homogène sur toute sa surface. On considère que les plans ont des dimensions infinies pour s'affranchir des effets de bords. En conséquence le flux entrant est égal au flux sortant, il n'y a pas de pertes de chaleur sur les bords.
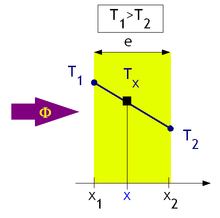
Notons la température du plan situé à l'abscisse , et la température du plan situé à l'abscisse . Notons l'épaisseur du mur. En régime stationnaire, T est une fonction affine de , d'où :
La densité de flux thermique surfacique s'écrit :
- .
Le flux thermique à travers une surface S vaut :
ou

Analogie électrique
Par analogie avec l'électricité (loi d'Ohm) dans le cas particulier où la surface de contact entre chaque matériau est constante (flux surfacique constant) nous pouvons mettre en parallèle les deux expressions :
Nous pouvons mettre en parallèle d'une part la tension et la température, d'autre part l'intensité et le flux thermique :
On peut définir alors une résistance thermique, jouant dans le transfert de chaleur un rôle comparable à la résistance électrique.
où est la surface du matériau et son épaisseur. La résistance thermique est homogène à des K⋅W−1
Surfaces planes en série

On considère des matériaux A, B et C d'épaisseur respective , et et de conductivité radiative respective , et .
Les hypothèses sont identiques à celles d'une surface plane simple. On considère que le contact entre chaque couche est parfait ce qui signifie que la température à l'interface entre 2 matériaux est identique dans chaque matériau (Pas de saut de température au passage d'une interface).
Enfin la surface de contact entre chaque matériau est constante ce qui implique un flux surfacique constant.
Les résistances thermiques s'additionnent :
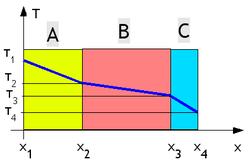
- Profil des températures
Pour chaque matériau la variation de température suit une loi du type :
La variation de température est donc linéaire dans l'épaisseur du matériau considéré. La pente dépend de λ (conductivité thermique) caractéristique de chaque matériau. Plus la conductivité thermique sera faible (donc plus le matériau sera isolant) plus la pente sera forte.
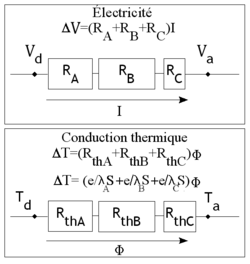
- Analogie électrique
De la même manière que les résistances électriques en série s'additionnent, les résistances thermiques en série s'additionnent.
Surfaces planes en parallèle

On considère des matériaux plans juxtaposés. Chaque matériau est homogène et limité par deux plans parallèles. C'est par exemple le cas d'un mur avec une fenêtre. Les hypothèses sont identiques à celles d'une surface plane simple. En supplément, on considère que la température est uniforme en surface de chaque élément (T1 et T2). Soit SA, SB et SC les surfaces respectives des éléments A, B et C.
Par la suite, on fait l'hypothèse que le flux est toujours perpendiculaire à la paroi composée ; ceci n'est pas réaliste puisque la température de surface de chaque élément qui la composent est différente et qu'il existe par conséquent un gradient de température latéral (à l'origine des ponts thermiques). Aussi, il est nécessaire de corriger le flux de chaleur calculé dans la paroi composée à l'aide de coefficients de déperdition linéiques, spécifiques à chaque jonction de paroi (et pouvant être négligeables, cf. règlementation thermique TH 2000)
Les conductances thermiques s'additionnent :
- Analogie électrique
Il est donc également possible de faire une analogie entre un montage électrique de résistances en parallèle.
 |
 |
Surface cylindrique simple

Le tube simple est constitué d'un seul matériau homogène. La température est homogène sur chaque surface du tube. On considère que le tube a une longueur infinie afin de s'affranchir des effets de bord. La variation de température s'écrit :
Surfaces cylindriques concentriques

Le tube concentrique est constitué de tubes disposés en couches concentriques. On considère que le contact est parfait entre les tubes. La température est homogène sur chaque surface du tube. On considère que le tube à une longueur L infinie afin de s'affranchir des effets de bord.
La résistance totale du tube s'exprime suivant une loi de type « série » comme le mur composé série :
Conduction en régime dynamique
La résolution de l'équation de la chaleur en régime dynamique est beaucoup plus délicate. Elle fait appel aux notions de transformées de Fourier, de produit de convolution et de distributions. Nous donnons quelques exemples de résolution.
Cas d'un domaine illimité
Principe général
Écrivons l'équation de la chaleur sous la forme :
où D est le coefficient de diffusivité thermique et P représente ici l'échauffement (en K/s) provenant de sources de chaleur. P peut être une fonction du temps et de la position de la source de chaleur, mais aussi une distribution. Par exemple, l'injection instantanée et ponctuelle d'une quantité de chaleur peut se représenter par le produit d'une distribution de Dirac à l'instant t = 0 par une distribution de Dirac en x = 0, x étant l'abscisse dans le cas d'un problème unidimensionnel ou le vecteur position dans le cas général.
On se donne également l'état initial du domaine , qui peut être également une fonction de x ou une distribution. On considère que T est nulle pour .
La méthode de résolution consiste à[16],[17] :
- appliquer une transformée de Fourier relative à la variable x, à tous les termes de l'équation différentielle. Cela transforme la dérivation par rapport à x par un produit. Si l'on prend , alors l'équation devient :
ou plutôt, au sens des distributions : pour tenir compte de la condition initiale ; - reconnaître dans cette équation un produit de convolution :
L'opérateur qu'on applique à F est un produit de convolution relatif à la variable t ; - appliquer la réciproque de l'opérateur dont on montre qu'il vaut , où H est la fonction de Heaviside, pour aboutir à :
Si F(P) est une fonction et non une distribution, cette relation devient, pour t > 0 : ; - prendre la transformée de Fourier inverse pour en déduire T.
Cas particulier

Si l'on prend et (injection instantanée de chaleur en un point donné), la méthode décrite ci-dessus conduit à :
donc, pour t > 0 :
dont la transformée de Fourier inverse est, pour t > 0 :
- dans le cas unidimensionnel ;
- dans le cas tridimensionnel.
Domaine illimité sans source de chaleur
Si l'on se donne seulement la température initiale du milieu sans source de chaleur (P = 0), alors on trouve que :
- dans le cas unidimensionnel.
- dans le cas tridimensionnel.
Cas de domaines limités, sans source de chaleur
Cas d'un domaine limité par un plan. Le problème de Kelvin

Supposons le domaine limité par le plan x = 0. Si l'on se donne pour condition aux limites supplémentaire T(0,t) = 0 pour tout t, alors, il suffit de prolonger la répartition initiale de température par une fonction impaire en x et d'appliquer le résultat précédent.
Le cas le plus célèbre est celui du problème de Kelvin. Ce dernier a considéré dans les années 1860 que la Terre était initialement à une température constante de l'ordre de 3 000 °C et qu'elle s'est refroidie par simple conduction. Utilisant la valeur actuelle du gradient de température en fonction de la profondeur, il en a déduit une estimation de l'âge de la Terre. On peut appliquer la méthode de résolution précédente en considérant la Terre comme plate et infiniment profonde, limitée par le plan de sa surface. Le calcul conduit à :
où erf est dite fonction d'erreur de Gauss.
Le gradient de température à la surface est :
Connaissant de l'ordre de 3 °C pour 100 mètres de profondeur et D estimé à 10−6 m2s−1, on trouve que vaut 100 millions d'années. Ce résultat est largement sous-estimé car Kelvin ignorait les phénomènes de convection au sein du manteau terrestre[18],[19],[20].
Cas d'un domaine limité par deux plans parallèles

Considérons un domaine limité par les deux plans x=0 et x=L. Supposons qu'on se donne comme conditions aux limites T(0,t) = T(L,t) = 0. On utilise une méthode de résolution basée sur les séries de Fourier, en cherchant T sous la forme :
Cette expression vérifie à la fois l'équation de la chaleur et les conditions aux limites. Si l'on se donne la répartition de température initiale , il suffit de développer celle-ci en série de Fourier pour déterminer les .
Par exemple, si l'on prend constant, on obtient :
En faisant tendre L vers l'infini, on retrouve la solution de Kelvin du paragraphe précédent, la somme précédente étant considérée comme une somme de Riemann convergeant vers l'intégrale.
Cas d'un domaine à géométrie sphérique

Dans le cas où la propagation se fait dans un domaine sphérique, et où la température ne dépend que de la distance r au centre, l'équation de la chaleur devient, compte tenu de l'expression du laplacien en sphérique :
Si l'on pose , l'équation devient :
On peut alors appliquer les méthodes précédentes pour déterminer F, puis en déduire T en divisant par r.
Ainsi, la résolution du problème de Kelvin dans le cas d'une boule de rayon R (température initiale uniformément égale à , la surface étant maintenue à une température nulle) conduit à l'expression suivante de T :
où sinc est la fonction sinus cardinal.
Cas de domaines limités, avec source de chaleur
On considère l'équation :
avec P non nul. On cherche en général une solution particulière à cette équation, de façon que, une fois retranchée à T, on puisse se ramener à une équation sans second membre. Voici quelques exemples, dans le cas où P représente une densité de source de chaleur constante, indépendante de la position et du temps.
Domaine limité par deux plans parallèles

Considérons un domaine limité par les deux plans x=0 et x=L. On suppose qu'à l'instant initial, la température du domaine est égale à une température de référence nulle, et que les bords du domaine resteront en permanence à cette température nulle. T vérifie donc :
- T(0,t) = T(L,t) = 0 pour tout t positif.
- T(x,0) = 0 pour tout x entre 0 et L.
La fonction indépendante de t vérifie les deux premières relations, de sorte que, si l'on pose , alors G vérifie :
On peut appliquer la méthode vue plus haut en cherchant G sous la forme d'une série :
qui vérifie les deux premières relations. Comme, pour des raisons de symétrie, on s'attend à ce que , on peut supposer que les coefficients sont nuls lorsque n est pair, de sorte que :
Pour t = 0, on a :
On trouve les en développant en série de Fourier. On trouve :
D'où G, puis finalement :
Lorsque t tend vers l'infini, la température du domaine tend vers , l'échauffement thermique dans le milieu étant alors en équilibre avec l'évacuation de la chaleur par les deux bords.
Domaine limité par un plan

La résolution du même problème dans le cas où x>0 consiste à déterminer T tel que :
- T(0,t) = 0 pour tout t positif.
- T(x,0) = 0 pour tout x > 0.
On peut obtenir la solution en faisant tendre L vers l'infini dans l'expression donnée dans le paragraphe précédent, en assimilant la série à une somme de Riemann. On obtient alors l'expression suivante :
erf est la fonction dite fonction d'erreur de Gauss. On peut également trouver cette expression en appliquant la méthode découlant du principe général relatif à un domaine illimité, après avoir étendu à l'espace entier les fonctions T et P en des fonctions impaires en x, de façon que T s'annule en x = 0.
Quand t tend vers l'infini, T vaut environ Pt, analogue à celle d'un domaine infini. Le bord unique n'est pas suffisant pour évacuer la chaleur.
Domaine à géométrie sphérique

Dans le cas d'un domaine dont le bord est une sphère de rayon R, on utilise l'expression du laplacien en sphérique et l'on est amené à résoudre :
- Pour tout t, T(R,t) = 0
- Pour tout r, T(r,0) = 0
En posant , G vérifie le système :
- Pour tout t, G(R,t) = 0
- Pour tout r,
La méthode des séries de Fourier suggère de chercher G sous la forme d'une série , où les sont trouvés en développant en série de Fourier. On obtient :
et donc :
où sinc est la fonction sinus cardinal.
Quand t tend vers l'infini, la température T tend vers la répartition limite .
Notes et références
- José-Philippe Pérez et A. M. Romulus, Thermodynamique. Fondements et applications, Paris, Masson, , p. 153.
- Pérez et Romulus 1993, p. 158
- Pérez et Romulus 1993, p. 160.
- Le terme système désigne un corps ou un ensemble de corps où s'opèreny des échanges de chaleur.
- Le diamant est une exception notable : son réseau cristallin rigide possède de nombreux mode de vibration quantifiés. Il en résulte que le diamant présente à la fois une capacité calorifique très faible et une conductivité thermique élevée.
- Voir Loi de Wiedemann et Franz.
- Joseph Fourier, Théorie analytique de la chaleur, [détail des éditions], Édouard Leroy, « Sur l’intégration des équations de la chaleur », ASENS, 3e série, t. 14, , p. 379-465 (lire en ligne) et liens externes (voir infra).
- (de) R. E. Peierls, « Zur kinetischen Theorie der Wärmeleitung in Kristallen », Annalen der Physik, vol. 3, , p. 1055–1101
- (en) Ingo Müller et Tommaso Ruggeri, Rational Extended Thermodynamics, vol. 37, Springer, coll. « Springer Tracts in Natural Philosophy », (ISBN 978-1-4612-7460-5)
- (en) Michael M. Modest, Radiative Heat Transfer, Academic Press, (ISBN 0-12-503163-7)
- (it) Carlo Cattaneo, « Sulla conduzione del calore », Atti del Seminario Matematico e Fisico dell' Universita di Modena e Reggio Emilia, vol. 3, , p. 83–101
- P. Vernotte, « Les paradoxes de la théorie continue de l'équation de la chaleur », Comptes-rendus de l'Académie des sciences, vol. 246, 1958 1958, p. 3154-3155
- (en) Yoseph Imry, Introduction to Mesoscopic Physics, Oxford University Press, (ISBN 0-19-850738-0, lire en ligne)
- (en) J. B. Pendry, « Quantum Limits to the Flow of Information and Entropy », Journal of Physics A: Mathematical and General, vol. 16, no 10, , p. 2161-2171 (lire en ligne)
- (en) K. Schwab, E. A. Enriksen, J. M. Worlock et M. L. Roukes, « Measurement of the Quantum of Thermal Conductance », Letters to Nature, vol. 404, , p. 974-977 (lire en ligne)
- Lev Landau et Evgueni Lifchits, Physique théorique, t. 6 : Mécanique des fluides [détail des éditions].
- Laurent Schwartz, Méthodes mathématiques pour les sciences physiques, Hermann, 1965.
- La convection apportant des matériaux chauds à proximité de la surface, le gradient de température au voisinage de celle-ci au bout d'un temps donné est plus élevé dans le cas de la convection que dans celui de la conduction. Par conséquent, la durée de refroidissement conduisant à un gradient donné sera estimée plus courte dans le cas de la conduction que dans celui de la convection. Voir England P, Molnar P, Richter F, Kelvin, Perry et l'âge de la terre, Pour la Science, février 2008, p. 32-37, traduit d'un article d'American Scientist. Une deuxième source d'erreur, plus marginale, provient du fait que Kelvin néglige également le terme de source d'énergie dû à la radioactivité.
- Jean-Louis Le Mouël, Le refroidissement de la Terre, 196e conférence de l’Université de tous les savoirs, 14 juillet 2000, [1] ou [2]
- John Perry, On the age of earth, 51, Nature (7 février 1895), 341-342
Voir aussi
Articles connexes
- Diffusivité thermique
- Diffusion de la matière
- Conductivité thermique
- Transfert thermique
- Conductance électrique
- Équation de la chaleur
- Thermodynamique hors équilibre
Liens externes
- cours bases essentielles http://www.ryounes.net/cours/conduction.pdf
- cours bases complètes : http://www.sciences.univ-nantes.fr/sites/claude_saintblanquet/index.htm
- http://www.lmm.jussieu.fr/~lagree/COURS/MECAVENIR


































![{\displaystyle {\begin{array}{rcl}{\frac {\partial E_{m}}{\partial t}}+{\frac {\partial \mathbf {\Phi } _{m}}{\partial x}}&=&\kappa \left(4\pi B_{m}-c_{m}E_{m}\right)\\[0.6em]{\frac {\partial \mathbf {\Phi } _{m}}{\partial t}}+c_{m}^{2}{\frac {\partial \mathbf {(} E_{m}{\mathsf {D}}_{m})}{\partial x}}&=&-c_{m}\kappa \mathbf {\Phi } _{m}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a917c9b167b49faf23aa35f27b3e0ad19f319060)









































































































































