Sinuosité
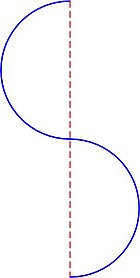
La sinuosité[1],[2], ou coefficient de sinuosité[3], ou indice de sinuosité[4],[5],[6], d’une courbe continûment dérivable comportant au moins un point d'inflexion est le rapport entre la longueur curviligne (selon le parcours) et la distance (ligne droite) entre les points extrêmes du tracé. Cette grandeur sans dimension est obtenue par le rapport suivant :
Caractéristiques[modifier | modifier le code]
La valeur varie entre 1 (ligne droite) et l'infini (cas d'une courbe fermée). La sinuosité de 2 demi-cercles inversés continus situés dans le même plan est de soit environ : elle est donc indépendante du rayon du cercle.
La courbe doit être continue (pas de saut) entre les deux extrémités. La valeur de la sinuosité est vraiment significative lorsque la ligne est toujours dérivable (pas de point anguleux intermédiaire). La distance entre les deux extrémités peut aussi s’évaluer par un cumul de segments selon une ligne brisée passant par les points d’inflexions successifs (sinuosité d'ordre 2).
Le calcul de la sinuosité est valable dans un espace à 3 dimensions (ex : pour l'axe central de l'intestin grêle) bien qu'il ne soit souvent effectué que dans un plan (avec alors une possible projection orthogonale de la courbe dans le plan retenu ; sinuosité "classique" sur plan horizontal, sinuosité de profil en long sur plan vertical). On peut aussi distinguer le cas où le flux s'écoulant sur la ligne ne pourrait physiquement pas parcourir la distance entre les extrémités : dans certaines études hydrauliques, ceci conduit à attribuer une "sinuosité" de 1 pour un torrent s'écoulant sur un substratum rocheux le long d'une projection horizontale rectiligne même si la pente varie (= si la sinuosité du profil en long est supérieure à 1).
La qualification d'une sinuosité (ex : forte / faible) dépend souvent de l'échelle cartographique du tracé et de la vitesse du flux / de l'objet qui s'y écoule (rivière, avalanche, voiture, cycliste, skieur, bobsleigh, TGV, etc.) : la sinuosité d'une même ligne courbe pourrait être considérée comme très forte pour une ligne de TGV mais faible pour une rivière. On voit néanmoins une très forte sinuosité dans la succession de méandres d'une rivière (ex : la Meuse dans les Ardennes), ou dans les virages en lacets de certaines routes de montagne. Le cortex cérébral de l'homme est fortement sinueux alors que celui des autres mammifères est "majoritairement lisse et plat"[7].
-
Traces sinueuses dans la neige profonde
Pour les cours d'eau, les classes classiques[8] de sinuosité, SI, sont :
- SI < 1,05 : quasi rectiligne
- 1,05 ≤ SI < 1,25 : sinueux
- 1,25 ≤ SI < 1,50 : très sinueux
- 1,50 ≤ SI : à méandres / méandriforme
Dans ce cas on mesure d'une part la longueur développée selon l'axe du lit mineur et d'autre part, entre les 2 mêmes points, celle selon l'axe général d'orientation du cours d'eau, soit selon la ligne moyenne de l'enveloppe de méandrage, soit selon la ligne passant par tous les points d'inflexion du lit[9].
Lorsque la sinuosité de la ligne est périodique, on peut en définir une longueur d'onde égale à la distance entre 2 sommets voisins. Son amplitude est alors la distance entre le maximum de l’onde et le segment entre deux points d'inflexion voisins. Dans le cas de plusieurs mêmes demi-cercles inversés continus situés dans le même plan, cette longueur d'onde est de 2 fois le diamètre et l'amplitude est d'un rayon du cercle.
Valeurs remarquables[modifier | modifier le code]
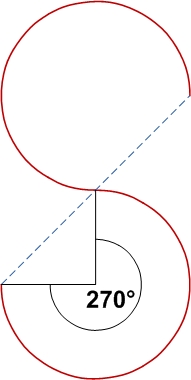
Avec deux arcs de cercle semblables opposés joints dans le même plan en continument dérivable :
| Angle au centre | Sinuosité | ||
|---|---|---|---|
| Degrés | Radians | Exacte | Décimale |
| 30° | 1.0115 | ||
| 60° | 1.0472 | ||
| 90° | 1.1107 | ||
| 120° | 1.2092 | ||
| 150° | 1.3552 | ||
| 180° | 1.5708 | ||
| 210° | 1.8972 | ||
| 240° | 2.4184 | ||
| 270° | 3.3322 | ||
| 300° | 5.2360 | ||
| 330° | 11.1267 | ||
Attention : avec 3 arcs de cercle semblables opposés joints inversés en continu dérivable et avec l'angle de 300° au centre, les courbes de la première partie de cercle et de la troisième vont tangenter : la courbe se fermant, la sinuosité de ces 3 arcs de cercle semblables passe alors à l'infini. Idem entre 300 et 360° puisque les première et troisième courbes se croisent. À 360°, les points 2 d'inflexion se rejoignant, disparaissant, on ne peut plus alors évoquer la sinuosité.
Notes et références[modifier | modifier le code]
- Denis Diderot et Jean Le Rond d' Alembert, Encyclopédie Ou Dictionnaire Raisonné Des Sciences, Des Arts Et Des Métiers, vol. 15, Samuel Faulche, , p. 219
- Jean-Gabriel Wasson, Jean-René Malavoi et Laurence Maridet, Impacts écologiques de la chenalisation des rivières, Antony/Lyon, Cemagref Editions, , 158 p. (ISBN 2-85362-502-8, lire en ligne), p. 134
- Jehad Kerbé, Climat, hydrologie et aménagements hydro-agricoles de Syrie, vol. 1, , 1228 p. (ISBN 2-86781-056-6), p. 671
- Jean-Jacques Bavoux, Initiation à l'analyse spatiale, Armand Colin, , 128 p. (ISBN 978-2-200-25845-0 et 2-200-25845-3, lire en ligne)
- Jean-Paul Amat, Charles Le Cœur et Lucien Dorize, Éléments de géographie physique, Bréal, , 463 p. (ISBN 978-2-7495-0205-2 et 2-7495-0205-5, lire en ligne), p. 183
- Hélène Roche, Premiers outils taillés d'Afrique, Nanterre, Société d'ethnographie, , 263 p. (ISBN 2-901161-14-6, lire en ligne), p. 109
- Vilayanur Ramachandran, Le cerveau fait de l'esprit : Enquête sur les neurones miroirs, Dunod, , 400 p. (ISBN 978-2-10-057211-3 et 2-10-057211-3, lire en ligne)
- Office français de la biodiversité, « Le méandrage » [PDF], sur le site OFB (consulté le ), p. 67
- Office français de la biodiversité, « Le méandrage » [PDF], sur le site OFB (consulté le ), p. 66


























