Dipôle électrostatique
Un article de Wikipédia, l'encyclopédie libre.
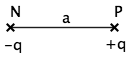
Un dipôle électrostatique se définit par une répartion inhomogène de charges électriques telles que le barycentre des charges positives ne coïncide pas avec celui des charges négatives. Le dipôle le plus simple est donc un couple de deux charge de signe opposé distants d'une longueur a non nulle quellconque. Cette notion est principalement utilisée en électromagnétisme et par suite en chimie où certaines liaisons entre molécules peuvent être expliquées en modélisant ces molécules par un dipôle (liaison hydrogène par exemple).
En physique, on s'intéresse au champ électrique E(r) créé en un point r éloigné du dipôle (on parle alors de dipôle actif). Mais on peut aussi étudier le comportement du dipôle lorsqu'il est placé dans un champ extérieur (on parle alors de dipôle passif).
Sommaire |
[modifier] Moment dipolaire
Quand un objet possède une charge électrique totale nulle (ce que l'on supposera par la suite), la grandeur qui définit un dipôle électrostatique est son moment dipolaire, généralement noté p ou d et donné par la formule :
,
où la somme court sur toute les charges électriques présentes. En particulier, en présence de deux charges opposées q et -q, situés aux points repérés par les rayons vecteurs r{ind|1}} et r2 respectivement,
.
Le moment dipolaire est exprimé en coulomb·mètre (C·m) ; par mesure de commodité, on l'exprime souvent debye (D), dont le facteur de conversion s'écrit :
- 1 D = 3,33564×10-30 C·m.
La principale propriété du moment dipolaire est que quand la charge totale est nulle, sa définition ne dépend pas de l'origine du système de coordonnées choisi. Il s'agit donc d'une quantité intrinsèque.
[modifier] Dipôle actif
[modifier] Potentiel généré
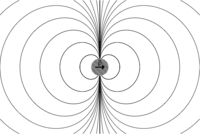
Le potentiel électrostatique V(r) créé par le dipôle en r est donné d'après la loi de Coulomb par :
.
En pratique, on s'intéresse en général au champ loin du dipôle lui même, de sorte que l'on peut développer les termes intervenant dans le potentiel. On suppose en outre que le point où est évalué le champ est très éloigné du dipôle. On peut effectuer le développement limité :
,
ce qui donne
.
On obtient alors la formule suivante :
,
où le premier terme de la somme est nul en vertude l'hypothèse que la charge totale est nulle.
[modifier] Champ électrique généré
La connaissance de V(r) permet de déduire directement le champ électrique E(r) par la formule du gradient :
.
[modifier] Dipôle passif
Soit un dipôle de moment dipolaire d placé en r où règne un champ extérieur non uniforme E(r). Si le champ n'est pas uniforme, la résultante des forces électrostatiques s'exerçant sur l'ensemble des charges est non nul, et vaut
.
De même, le dipôle subit aussi un moment Γ donné par
.
Enfin, dans le cas où le dipole est considéré comme rigide (le moment dipolaire ne dépend pas du champ électrique extérieur), on peut lui associer une énergie potentielle électrique donnée par
.
Ainsi, le dipôle va-t-il minimiser son énergie quand il va s'aligner parallèlement au champ.
[modifier] Cas non statique
Quand le dipôle est en mouvement non uniforme, ou bien que la distribution de ses charge évolue au cours du temps, le champ électromagnétique qu'il génère prend une forme plus complexe. On peut lors montrer que le dipôle est le siège d'une émission d'énergie appelée rayonnement dipolaire électrique.
