Courbe algébrique
En mathématiques, et plus précisément en géométrie algébrique, une courbe algébrique est une variété algébrique (ou un schéma de type fini) sur un corps, dont les composantes irréductibles sont de dimension 1. Cette définition est la généralisation moderne de celle des courbes algébriques classiques, telles que les coniques, définies, dans le cas des courbes planes, comme l'ensemble des points solutions d'une équation polynomiale.
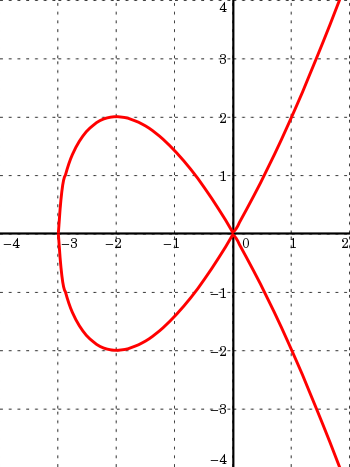
Définition et exemples[modifier | modifier le code]
Sous sa forme la plus générale, une courbe algébrique sur un corps est une variété algébrique de dimension 1 sur , séparée pour éviter des pathologies. En considérant les composantes irréductibles munies de la structure réduite, on se ramène aux courbes intègres. Par compactification et normalisation, on se ramène aux courbes projectives régulières, ce qui est la situation le plus couramment abordée. En dehors des variétés algébriques de dimension 0 qui se réduisent aux algèbres finies sur un corps, les courbes sont les premières variétés algébriques non triviales.
Courbes rationnelles[modifier | modifier le code]
On appelle courbe rationnelle, ou encore courbe unicursale, toute courbe birationnellement équivalente à une droite (projective), que l'on peut identifier au corps des fractions rationnelles à une indéterminée, k(x). Si k est algébriquement clos, c'est équivalent à être une courbe de genre zéro ; cependant, le corps R(x,y) avec x2 + y2 = −1 est une courbe de genre zéro qui n'est pas un corps de fonctions rationnelles.
Concrètement, une courbe rationnelle de dimension n sur k peut être paramétrée (sauf pour des points isolés exceptionnels) au moyen de n fonctions rationnelles définies à l'aide d'un unique paramètre t ; multipliant par les dénominateurs communs, on se ramène à n+1 fonctions polynomiales dans un espace projectif.
Les premiers exemples sont :
- la droite affine dont les points rationnels correspondent à l'ensemble . C'est une courbe algébrique affine ;
- la droite projective dont les points rationnels correspondent à la droite projective ordinaire , c'est-à-dire l'ensemble des droites de l'espace vectoriel . C'est la courbe projective la plus simple.
Toute conique définie sur k et ayant un point rationnel dans k est une courbe unicursale, qui peut être paramétrée en déterminant l'autre intersection de la courbe avec une droite de pente t passant par le point rationnel, ceci donnant un polynôme de degré 2 à coefficients k-rationnels ayant une racine k-rationnelle ; l'autre racine est donc également rationnelle.

Considérons par exemple l'ellipse x2 + xy + y2 = 1, pour laquelle (−1, 0) est un point rationnel. La droite de pente t passant par (−1, 0) a pour équation y = t(x + 1). Substituant et résolvant en x, on obtient
- , et donc ;
cette paramétrisation rationnelle montre que l'ellipse est une courbe unicursale. Tous les points de l'ellipse sont ainsi obtenus, sauf le point (−1, 1), qui correspond à t = ∞ ; la courbe entière est donc paramétrée par la droite projective réelle (ou, plus généralement, par k complété par un point à l'infini ; si l'on se place dans le cas complexe, c'est une paramétrisation par la sphère de Riemann).
Ces paramétrisations permettent de résoudre des équations diophantiennes homogènes. Ainsi, à partir des équations précédentes, on obtient
et ces nombres vérifient
- ;
X, Y et Z sont entiers si t est entier, et le paramétrage précédent permet de montrer qu'il n'y a pas d'autres solutions entières. Ainsi, appliquant le théorème d'Al-Kashi, on construit tous les triangles à côtés entiers dont l'un des angles est 60°, comme le triangle de côtés 3, 7, et 8 (obtenu en prenant t = 2) puisque 82 − 3×8 + 32 = 72.
De nombreuses autres courbes classiques sont unicursales ; c'est le cas du folium de Descartes, de la deltoïde ou des courbes de Lissajous; voici (en anglais) une liste plus complète.
Courbes elliptiques[modifier | modifier le code]
Une courbe elliptique peut être définie comme une courbe algébrique de genre 1 ayant un point rationnel : elles ont toutes pour modèle commun les cubiques non singulières. On prend souvent dans ce cas comme point rationnel un point d'inflexion à l'infini ; cela revient à écrire la courbe sous la forme de Tate-Weierstrass, dont la version projective est
Les courbes elliptiques sont munies d'une structure de groupe abélien, le point distingué étant l'élément neutre du groupe ; dans le modèle cubique, trois points sont de somme nulle (pour la loi du groupe) si et seulement s'ils sont colinéaires. Pour les courbes elliptiques définies dans le plan complexe, le groupe est isomorphe au quotient du groupe additif des complexes par le réseau des périodes fondamentales de la fonction elliptique correspondante.
Courbes de genre > 1[modifier | modifier le code]
Les courbes de genre supérieur à 1 sont qualitativement différentes des précédentes. Définies sur les rationnels, le théorème de Faltings montre qu'elles ne peuvent avoir qu'un nombre fini de points rationnels ; elles peuvent être munies d'une structure hyperbolique. Des exemples importants sont les courbes hyperelliptiques, la quartique de Klein, et la courbe de Fermat (en) , avec .
Dans toute la suite, sauf dans la dernière section, on se placera dans le cadre des courbes projectives irréductibles et lisses sur un corps . On sait que cela implique que est régulière. Pour simplifier on suppose de plus que (donc reste irréductible sur la clôture algébrique de ).
Correspondance entre courbes et corps de fonctions[modifier | modifier le code]
Pour toute courbe (projective régulière et irréductible), son corps des fonctions rationnelles est un corps de fonctions d'une variable.
Si est un morphisme entre deux courbes (projectives régulières irréductibles), il est soit constant, soit dominant. Dans ce dernier cas, induit un morphisme des corps des fonctions rationnelles qui fait de une extension finie de
On obtient ainsi un foncteur de la catégorie des courbes projectives régulières irréductibles, dont les morphismes sont les morphismes non-constants de -schémas, vers la catégorie des corps de fonctions d'une variable, dont les morphismes sont les morphismes de -extensions.
Théorème — Le foncteur ci-dessus est une équivalence de catégories.
Concrètement, cela veut dire que la donnée d'une courbe est équivalente à la donnée de son corps de fonctions, et que la donnée de morphismes non-constant est équivalente à la donnée d'extensions finies de corps de fonctions.
Note : si n'est pas parfait, il existe des corps de fonctions d'une variable qui ne soient pas des corps des fonctions rationnelles de courbes projectives lisses irréductibles. En revanche, si est parfait, il n'y a pas de distinction entre régulier et lisse.
Définition — Soit un morphisme non-constant. On appelle degré de le degré de l'extension de corps correspondante. Un morphisme est degré 1 si et seulement si c'est un isomorphisme.
Diviseurs[modifier | modifier le code]
Un diviseur sur est une somme (formelle) finie à coefficients entiers, indexée par des points (fermés) de . Les sont tous nuls sauf pour un nombre fini d'entre eux. Le coefficient se note aussi . C'est la valuation de en . L'ensemble des diviseurs forment un groupe abélien libre dont une base est constituée des classes , . Un diviseur est dit effectif si les coefficients qui interviennent sont tous positifs ou nuls.
On définit le degré de par
où est le corps résiduel en , extension finie de par le théorème des zéros de Hilbert. L'application degré est un morphisme de groupes . Le noyau de ce morphisme est donc un groupe.
Il y a un type particulièrement important de diviseurs, les diviseurs principaux. Il s'agit des diviseurs associés aux fonctions rationnelles non nulles . Par définition, où est l'ordre d'annulation de en si est régulière en , et c'est l'opposé de son ordre de pôle sinon.
On montre que tout diviseur principal est de degré . L'ensemble des diviseurs principaux forment un sous-groupe du groupe . Le quotient de par les diviseurs principaux s'injecte dans , où est la jacobienne de . C'est un isomorphisme si est algébriquement clos ou si a un point rationnel.
On dit que deux diviseurs sur sont linéairement équivalents s'ils diffèrent par un diviseur principal.
Si est un diviseur, on lui associe un faisceau inversible sur de la manière suivante: pour tout ouvert affine de , est égal à l'union de 0 avec l'ensemble des fonctions rationnelles non-nulles vérifiant pour tout .
Inversement, tout faisceau inversible est isomorphe à un , étant unique à équivalence linéaire près.
Diviseur canonique — Le faisceau des formes différentielles sur est un faisceau inversible. C'est le fibré cotangent sur . Il lui correspond donc un diviseur , unique à équivalence linéaire près. Un tel diviseur est appelé un diviseur canonique de .
Théorème de Riemann-Roch[modifier | modifier le code]
Le théorème de Riemann-Roch donne une estimation de la dimension de l'espace des fonctions rationnelles à pôles contrôlés par un diviseur donné. C'est un résultat fondamental dans l'étude des courbes algébriques. Concrètement, on se donne des points dans , et on leur affecte des coefficients entiers . Soit le diviseur somme des . Alors est par définition l'ensemble des fonctions rationnelles nulle ou vérifiant l'inégalité pour tout (plus synthétiquement : ). C'est un espace vectoriel sur le corps de base , de dimension finie que l'on note . On a les propriétés suivantes :
- Si et sont linéairement équivalentes, alors .
- . En particulier, si est négatif.
- si et seulement si est linéairement équivalent à un diviseur effectif.
- , où est le genre de la courbe, défini comme étant . C'est la forme faible du théorème de Riemann-Roch.
Théorème de Riemann-Roch — On a l'égalité
Corollaire :
- on a ;
- si , alors .
Définition — Une courbe hyperelliptique est une courbe de genre au moins 2, dont le corps de fonction est une extension (nécessairement séparable) de degré 2 du corps des fractions rationnelles . Cela revient donc à dire que admet un morphisme de degré 2 vers . Attention cependant que certains auteurs appellent plus généralement courbes hyperelliptiques celles qui admettent un tel morphisme défini sur la clôture algébrique de .
Exemples
- Une courbe projective plane donnée par une équation homogène de degré est de genre .
- Une courbe hyperelliptique correspondant à une extension (en caractéristique différente de 2) avec séparable de degré , est de genre . Une base des formes différentielles est donnée par .
- Sur la droite projective, le diviseur canonique est linéairement équivalent à si est un point rationnel quelconque.
Classification des courbes projectives lisses[modifier | modifier le code]
Un premier invariant pour distinguer les courbes algébriques entre elles est le genre, qui rappelons-le, est la dimension de l'espace vectoriel des formes différentielles sur la courbe. C'est donc un entier positif ou nul.
Les courbes de petit genre[modifier | modifier le code]
- On a si et seulement si est une conique (non-dégénérée). Une conique est isomorphe (en tant que variété algébrique) à la droite projective si et seulement si elle possède un point rationnel. Le diviseur canonique sur une courbe de genre 1 est le diviseur nul.
- Si et si a un point rationnel, alors possède une structure de courbe elliptique. Dans le cas général, la jacobienne de est une courbe elliptique et est un torseur (espace homogène principal) sous (grosso modo, opère transitivement et librement sur ).
- Si , alors est une courbe hyperelliptique.
- Pour tout , il existe une courbe de genre . Pour , il suffit de considérer une courbe hyperelliptique définie par avec séparable de degré et ou 0, selon que est de caractéristique 2 ou non.
- Les courbes de genre 3 sont soit hyperelliptique sur la clôture algébrique de , soit une courbe plane de degré 4.
Espace de modules des courbes de genre g[modifier | modifier le code]
Un espace de modules est une variété algébrique ou plus généralement un schéma dont les points correspondent à une classe d'objets provenant de la géométrie algébrique. Un espace de module est dit fin lorsqu'il représente un foncteur de la catégorie des variétés algébriques dans la catégorie des ensembles.
Fixons le corps de base et un genre . On peut considérer l'ensemble des classes d'isomorphes des courbes de genre sur . On montre qu'il existe une variété algébrique intègre, normale et quasi-projective sur tel qu'il existe une application naturelle (naturelle veut dire une compatibilité avec les extensions de corps de base), qui soit une bijection sur un corps algébriquement clos. Cette variété s'appelle l'espace de modules des courbes de genre . Elle est de dimension 0 si , de dimension 1 (et même isomorphe à la droite affine) si (sur un corps algébriquement clos, toute courbe de genre 1 est une courbe elliptique, et sa classe d'isomorphisme est détermnée par l'invariant modulaire ). En genre au moins 2, est de dimension . Moralement, il suffit de paramètres (et des relations algébriques) pour décrire l'ensemble des courbes de genre .
L'espace de modules est dit grossier car il ne représente pas le foncteur des courbes projectives lisses de genre (lequel foncteur n'est tout simplement pas représentable), mais ses points sur un corps algébriquement clos sont en bijection avec l'ensemble , et la variété est en un sens minimal pour cette propriété.
Notons que contrairement aux surfaces topologiques, ce qui précède dit que le genre (à partir de 1) ne détermine absolument pas la courbe à isomorphisme près.
Groupe des automorphismes[modifier | modifier le code]
Tout automorphisme de se prolonge en un automorphisme de . On se limite donc aux courbes sur un corps algébriquement clos.
- Le groupe des automorphismes de la droite projective est isomorphisme au groupe des homographies .
- Supposons de genre 1 et désignons arbitrairement un point . Pour éviter les confusions possibles, on va noter par la courbe elliptique constituée de avec comme élément neutre. Alors le groupe s'insère dans une suite exacte
la dernière flèche envoyant un automorphisme sur . Le groupe est en général le groupe cyclique d'ordre 2, et peut être exceptionnellement cyclique d'ordre 4 ou 6. Si le corps est de caractéristique 2 ou 3, ce groupe peut aussi être d'ordre 12 ou 24.
- Si est de genre , alors est un groupe fini. Si de plus, le corps de base est caractéristique nulle, alors l'ordre du groupe est borné par . En caractérisitique positive cette borne linéaire n'est plus valable. Il faut lui substituer une borne polynomiale du type avec une constante explicite de l'ordre de 14x16.
- Si et si est suffisamment générale, alors est trivial. Plus précisément, il existe un ouvert dense de l'espace de modules tel que la conclusion ci-dessus tienne pour toute courbe induisant un point dans .
Plongement dans un espace projectif[modifier | modifier le code]
- Sur un corps infini, toute courbe projective lisse se plonge dans .
De façon plus canonique :
- si , le diviseur canonique induit un plongement dans si et seulement si la courbe n'est pas hyperelliptique (sur ).
- si , alors (qui correspond à la puissance tensorielle ) induit un plongement de la courbe dans .
Courbes sur des corps particuliers[modifier | modifier le code]
Sur les nombres complexes[modifier | modifier le code]
Sur les corps globaux[modifier | modifier le code]
Mordell-Weil, Mordell
Sur les corps finis[modifier | modifier le code]
Comptage des points : hypothèse de Riemann sur un corps fini.
Cas général[modifier | modifier le code]
Régularité[modifier | modifier le code]
Soit X une variété algébrique intègre de dimension 1. Alors les propriétés suivantes sont équivalentes
- X est normale (c'est-à-dire que pour tout ouvert affine U, l'anneau OX(U) est intégralement clos) ;
- OX(U) est un anneau de Dedekind pour tout ouvert affine U ;
- l'anneau local OX,x est un anneau de valuation discrète pour tout point fermé x ;
- X est une variété algébrique régulière, c'est-à-dire que OX,x est un anneau local régulier pour tout point x.
Si le corps de base k est parfait, ces propriétés sont équivalentes à
- X est non singulière (ou lisse), c'est-dire qu'après extension du corps de base à la clôture algébrique de k, la variété est régulière.
Projectivité[modifier | modifier le code]
Une courbe algébrique est projective si et seulement si elle est propre. Elle est propre si et seulement si chaque composante irréductible est propre. Une courbe irréductible est propre si et seulement si elle n'est pas affine.[source insuffisante]
Ainsi une courbe algébrique intègre est soit affine, soit projective.
Courbes singulières ou non projectives[modifier | modifier le code]
Si est une courbe algébrique séparée, alors elle est quasi-projective. Si aucune de ses composantes irréductibles n'est projective, alors elle est affine.
Une courbe peut présenter des singularités, au si on prend sa normalisation , alors est un morphisme fini surjectif, et est une courbe régulière.






















![{\displaystyle D=\sum _{x}a_{x}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bfc9f95d08521834d17d782e48f2521166afc2e)





![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)

![{\displaystyle \deg(D)=\sum _{x}a_{x}[k(x):k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b08574ea4fd0554a90ff41bd63b7bc2eeb19b56)






![{\displaystyle (f)=\sum _{x}\mathrm {ord} _{x}(f)[x],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e06a162064964610043d1b415f08c62b30e4c37)
















![{\displaystyle n_{i}[x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c0ecb378fe875c7bc4162000618f6098ba5126e)






















![{\displaystyle f(x)\in k[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00b8295885af09a1a70a9008da19b502616b66e4)

![{\displaystyle g=[(d-1)/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d495bf423bb73031da0984a4cd9b05c4668bfcfc)

![{\displaystyle -2[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3098285463572f142900ede80c8bc263ae4cc2d1)



































