Calendrier perpétuel

Un calendrier perpétuel indique le jour de la semaine pour n'importe quelle date, « quelle que soit l'année » par opposition au calendrier courant qui se limite à l'année en cours.
Pour les calendriers grégorien et julien, un calendrier perpétuel se compose généralement de l'une des trois variantes générales:
- 14 calendriers d'un an, plus un tableau indiquant quel calendrier d'un an doit être utilisé pour une année donnée. Ces calendriers d'un an se divisent également en deux ensembles de sept calendriers: sept pour chaque année commune (année qui n'a pas de 29 février), chacun des sept commençant à un jour différent de la semaine, et sept pour chaque année bissextile, encore une fois avec chacun commençant un jour différent de la semaine, totalisant quatorze ans. (Voir la lettre dominicale pour un schéma de dénomination commun pour les 14 calendriers.)
- Sept calendriers d'un mois (31 jours) (ou sept de chaque mois de 28 à 31 jours, pour un total de 28) et un ou plusieurs tableaux pour montrer quel calendrier est utilisé pour un mois donné. Les tableaux de certains calendriers perpétuels glissent l'un contre l'autre, de sorte que l'alignement de deux échelles l'une sur l'autre révèle le calendrier mensuel spécifique via un pointeur ou un mécanisme de fenêtre. [1] Les sept calendriers peuvent être combinés en un seul, soit avec 13 colonnes dont sept seulement sont révélées, soit avec des noms de jour de la semaine mobiles (comme indiqué sur l'image du calendrier perpétuel de poche).
- Un mélange des deux variantes ci-dessus - un calendrier d'un an dans lequel les noms des mois sont fixes et les jours de la semaine et les dates sont indiqués sur des pièces mobiles qui peuvent être échangées si nécessaire.
Un tel calendrier perpétuel n'indique pas les dates des fêtes mobiles telles que Pâques, qui sont calculées sur la base d'une combinaison d'événements de l'année tropicale et des cycles lunaires. Ces problèmes sont traités en détail dans Computus.
Le Nürnberger Handschrift GNM 3227a est un exemple précoce de calendrier perpétuel pour une utilisation pratique. Le calendrier couvre la période de 1390 à 1495 (raison pour laquelle le manuscrit est daté d'environ 1389). Pour chaque année de cette période, il énumère le nombre de semaines entre le jour de Noël et la Quinquagesima. Il s'agit du premier exemple connu d'une forme tabulaire de calendrier perpétuel permettant le calcul des fêtes mobiles devenues populaires au XVe siècle.
Le calendrier perpétuel de G.D. Moret
[modifier | modifier le code]Ce calendrier consiste en une série de trois tableaux dans lesquels on choisit successivement le siècle, l'année, le mois et le quantième (jour du mois). On obtient un nombre de 0 à 6 (soit 7 possibilités) qui correspond au jour de la semaine.
Version par tableaux
[modifier | modifier le code]- Mode d'emploi
Il y a lieu de procéder en trois étapes :
- Trouver dans le tableau 1 le chiffre à l'intersection des centaines (millésimes) et de l'année. On l'appelle le chiffre "A". (Ce chiffre peut être : 0, 1, 2 , 3, 4, 5 ,6). Dans ce tableau s'est glissé une erreur : le chiffre de la première ligne et première colonne (année 1790 par exemple) est indiqué être un 0 (zéro), mais devrait être un 6 (six). Pour s'en persuader, il suffit de calculer le jour des 4 dates suivantes : 31/12/1789 & 01/01/1790, 31/12/1790 & 01/01/1791.
- Trouver dans le tableau 2 le chiffre à l'intersection de la ligne de A et de la colonne du mois. On l'appelle le chiffre "B". Pour ce faire, partir de la colonne de gauche en utilisant le chiffre "A" obtenu étape 1. (Le second chiffre obtenu peut être : 0, 1, 2, 3, 4, 5, 6).
- Trouver dans le tableau 3 le jour à l'intersection de la ligne de B et de la date recherchée. Pour ce faire, partir de la colonne de gauche en utilisant le chiffre "B" obtenu étape 2.
- Tableau 1
- millésimes et années
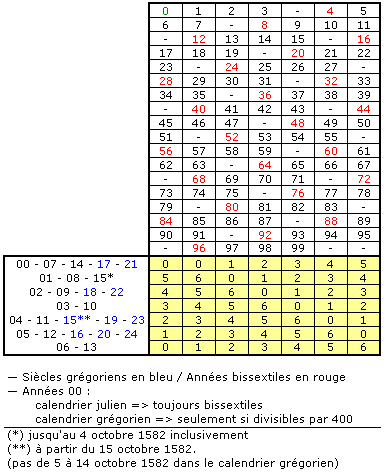
- Tableau 2
- mois

- Tableau 3
- jours
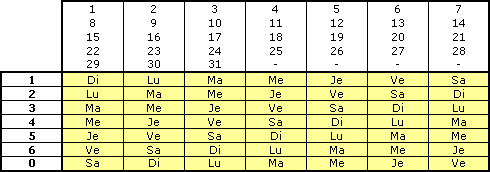
Version mémorisable
[modifier | modifier le code]La méthode proposée ci-dessous est une version mémorisable du calendrier Moret : elle supprime ou simplifie les tableaux en faisant appel à la logique et au calcul mental.
Cette méthode attribue un numéro au siècle, à l'année, au mois et au quantième. En additionnant les quatre nombres, on obtient le jour de la semaine. On peut aussi utiliser cette méthode pour faire des calculs inverses : quels sont les mois qui contiennent un vendredi 13 ? dans combien d'années retrouvera-t-on les mêmes dates ?
Tous ces numéros sont définis modulo 7, c'est-à-dire que 5 est équivalent à 12, 19, 26… Le résultat final de l'addition donne le jour de la semaine, en donnant à lundi le nombre 1. Un résultat final de 12 ou de -2 correspondra donc par exemple à 5, c'est-à-dire vendredi.
Nombre séculaire
[modifier | modifier le code]Le « nombre séculaire » est le même pour toutes les années commençant par les deux mêmes chiffres. On rattache donc ici l'an 2000 aux années 2001 à 2099 bien qu'il ne fasse pas formellement partie du XXIe siècle. Le calcul est différent dans le calendrier julien et dans le calendrier grégorien (pour les dates de passage du calendrier julien au calendrier grégorien en dehors de la France, voyez Passage au calendrier grégorien).
- Calendrier julien (jusqu'au en France). Le nombre séculaire est égal à : 19 moins les deux premiers chiffres de l'année.
Exemple : pour les années 1200 à 1299, le nombre séculaire est 19 - 12 = 7
- Calendrier grégorien (depuis le en France). Le tableau suivant donne les nombres séculaires pour chaque siècle :
1582 à 1599 : 1
1600 à 1699 : 0
1700 à 1799 : 5
1800 à 1899 : 3
1900 à 1999 : 1
2000 à 2099 : 0
2100 à 2199 : 5
Remarque : ce nombre diminue de deux unités chaque siècle, sauf lorsque les deux premiers chiffres sont un multiple de 4 (1600 à 1699, 2000 à 2099).
Nombre annuel
[modifier | modifier le code]Le tableau suivant donne les années pour lesquelles le nombre annuel est égal à 0. À partir de ces années, le nombre annuel augmente d'une unité chaque année, et de deux si l'année est bissextile. Si on ne souhaite pas apprendre par cœur ce tableau, on peut noter que ces années se retrouvent tous les 28 ans (7 jours de la semaine x 4 années entre deux bissextiles).
| ..04 | ..10 | ||
| ..21 | ..27 | ..32 | ..38 |
| ..49 | ..55 | ..60 | ..66 |
| ..77 | ..83 | ..88 | ..94 |
Exemple : l'année 2010 a un nombre annuel de 0, l'année 2015 de 6 et l'année 2016 de 1 (8 modulo 7) parce qu'il faut compter les années bissextiles 2012 et 2016.
On peut aussi remarquer que le résultat est donné par la formule suivante : pour l'année a, on calcule la division euclidienne de a par 4 (c'est-à-dire le nombre c quand on écrit a=4c+r, avec r plus petit que 4), et le nombre annuel est alors donné par le reste de la division euclidienne de a+c-5 par 7. Dans les exemples précédents, on trouve : a=10, donc c=2 puis a+c-5=7 dont le reste dans la division par 7 est bien 0 ; et pour le deuxième : a=16, donc c=4, puis a+c-5=15 dont le reste dans la division par 7 est 1 ; qui est bien équivalent à 8 modulo 7.
Remarque : si deux années ont la même somme nombre séculaire + nombre annuel, un calendrier des Postes utilisé la première année sera aussi valable pour l'autre, sauf dans le cas où une et une seule de ces deux années est bissextile.
Nombre mensuel
[modifier | modifier le code]Le tableau suivant donne le nombre mensuel pour chaque mois de l'année :
| Mois | Nombre mensuel |
| février (année non bissextile), mars, novembre | 0 |
| juin | 1 |
| septembre, décembre | 2 |
| janvier (année bissextile), avril, juillet | 3 |
| janvier (année non bissextile), octobre | 4 |
| mai | 5 |
| février (année bissextile), août | 6 |
Exemple : le mois de janvier a un nombre mensuel de 4 en 2003 et de 3 en 2004 (année bissextile).
Quantième
[modifier | modifier le code]Le dernier chiffre est le quantième lui-même, c'est-à-dire le numéro du jour dans le mois.
Exemples
| Jour | nombre séculaire | + | nombre annuel | + | nombre mensuel | + | quantième | = | résultat (jour de la semaine) |
| 0 | + | 5 | + | 4 | + | 8 | = | 17 = 2x7 + 3 (mercredi) | |
| (calendrier julien) | 4 | + | 6 | + | 2 | + | 9 | = | 21 = 3x7 + 0 (dimanche) |
| (calendrier grégorien, lendemain du en France) | 1 | + | 6 | + | 2 | + | 20 | = | 29 = 4x7 + 1 (lundi) |
| 1 | + | 4 | + | 3 | + | 21 | = | 29 = 4x7 + 1 (lundi) | |
| Combien y a-t-il de vendredi 13 en l'an 2003 ? Si l'on fait le calcul précédent en remplaçant le nombre mensuel par M, on obtient l'addition suivante : | |||||||||
| vendredi 13 en 2003 | 0 | + | 5 | + | M | + | 13 | = | 5 (vendredi) |
| d'où M = -13 = 1 - 2x7. Le nombre mensuel 1 correspond au seul mois de juin. | |||||||||
Version variante mémorisable (calendrier grégorien)
[modifier | modifier le code]Cette version, semblable à la précédente dans les principes, réduit les efforts de mémoire pour faciliter le calcul mental. Elle consiste, pour une date donnée, à effectuer dans l'ordre les ajouts ou cumuls suivants (en ne retenant que les restes dans la division par 7) :
- La somme du nombre formé par les deux derniers chiffres de l'année plus la partie entière de son quart.
- Une correction séculaire évaluée à la 6 4 2 et 0 (0 à partir de 1900, 6 à partir de 2000, 4 à partir de 2100, 2 à partir de 2200 et à nouveau 0 à partir de 2300... etc. mais aussi 0 à partir de 1582 année de création du calendrier, 6 à partir de 1600, ... ).
- Le décalage du mois qui répond à la suite 033 614 625 035 (on ajoute 0 en janvier, 3 en février, ... 5 en décembre).
- Le quantième du jour.
Le nombre obtenu correspond au jour de la semaine : 1 pour un lundi, 2 pour un mardi, ... et 7 ou 0 pour un dimanche, avec une seule exception : retrancher 1 en janvier et février des années bissextiles (à appliquer de préférence en 1 lorsque la division tombe juste sauf exceptions séculaires).
Exemple 1 : Quel jour était le ? Année 89 ⇒ (70)+19 ⇒ (14)+5 ⇒ 5, son quart 22 ⇒ (21)+1 ⇒ 1, donc 5+1=6 plus le siècle ⇒ 4, soit 10⇒3, le mois de juillet ⇒ 6, d'où 9 ⇒ 2, le quantième (14 ⇒ 0) résultat 2. C'était un mardi !
Exemple 2 : Quel jour était le ? Année⇒4 son quart⇒1, leur somme⇒5, siècle 18⇒2, cumul 5 et 2⇒7⇒0, décembre⇒5, quantième le 2. C'était un dimanche !
Finalement, hormis la méthode dont la mémorisation peut-être facilitée par la compréhension (voir la discussion), le seul effort de mémoire à effectuer consiste à retenir la suite des décalages mensuels.
Voir aussi
[modifier | modifier le code]Articles connexes
[modifier | modifier le code]- Calendrier
- Calendrier grégorien (Passage au calendrier grégorien)
- Calendrier julien
- Calendrier universel
- Calendrier fixe
- Détermination du jour
- Algorithme du jour du Jugement dernier
Liens externes
[modifier | modifier le code]- Calendrier perpétuel de 1753 à 2199
- Calendrier perpétuel de -3999 à +3999, logiciel libre à installer.
- Calendrier perpétuel juif
- Calendrier perpétuel musulman Conversion d'une date du calendrier grégorien en date du calendrier hégirien.
