Flexion (matériau)


En physique (mécanique), la flexion est la déformation d'un objet sous l'action d'une charge. Elle se traduit par une courbure. Dans le cas d'une poutre, elle tend à rapprocher ses deux extrémités. Dans le cas d'une plaque, elle tend à rapprocher deux points diamétralement opposés sous l'action.
L'essai de flexion d'une poutre est un essai mécanique utilisé pour tester la résistance en flexion. On utilise la flexion dite « trois points » et la flexion dite « quatre points ».
En chaudronnerie, le pliage d'une tôle est une flexion pour laquelle on veut dépasser la limite élastique du matériau, afin d'avoir une déformation définitive (déformation plastique). Dans la plupart des autres cas, on cherche au contraire les conditions nécessaires pour ne pas dépasser la limite élastique, afin de préserver l'intégrité de la pièce.
Cas d'une poutre[modifier | modifier le code]

En théorie des poutres, on considère des fibres, c'est-à-dire des petits cylindres de matières générés par une portion dS et une courbe parallèle à la courbe moyenne (la « direction de la poutre ») ; la courbe moyenne passe par les centres de gravité des sections droites (sections perpendiculaires à la courbe moyenne). Les fibres situées vers l'extérieur de la flexion sont en extension, elles sont soumises à de la traction. Les fibres situées à l'intérieur de la flexion sont en compression.
La fibre engendrée par la courbe moyenne est appelée « fibre neutre ». Elle garde sa longueur lors de la flexion.
Par la suite, sauf mention contraire, nous supposerons que la poutre est rectiligne avant la flexion (la courbe moyenne forme une droite) et que les sections sont symétriques. Nous considérerons au début la flexion plane, c'est-à-dire avec des charges agissant dans un plan de symétrie de la poutre.
Déformation[modifier | modifier le code]
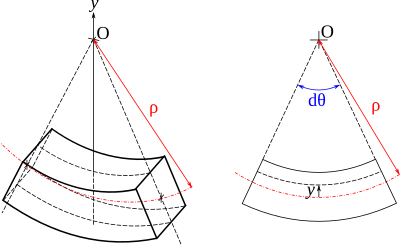
Du fait de l'hypothèse de Bernoulli (lors de la déformation, les sections planes perpendiculaires à la fibre moyenne restent planes et perpendiculaires à la fibre moyenne),
- la fibre neutre a un allongement nul ;
- les fibres à l'extérieur de la courbure sont étirées ;
- les fibres à l'intérieur de la courbure sont comprimées.
la déformation longitudinale ε varie de manière linéaire en fonction de y.

Par ailleurs, en considérant une poutre droite, si l'on appelle uy(x) la flèche, c'est-à-dire le déplacement vertical du point de la courbe moyenne situé à l'abscisse x en raison de la flexion, on a, d'après la définition générale du rayon de courbure :
- .
Le graphique uy(x) donne la forme de la courbe moyenne, encore appelée « déformée de la poutre ».
Efforts de cohésion[modifier | modifier le code]

Si l'on considère les efforts de cohésion (voir les articles Théorie des poutres et Torseur de cohésion), la flexion résulte des moments fléchissants Mfy et Mfz.
Nous considérerons ici la convention des efforts à droite.
On remarque que la valeur de l'effort tranchant est la dérivée du moment fléchissant par rapport à la position x du point considéré :
- .
Le diagramme des moments fléchissants peut être établi par la méthode du funiculaire.
Contraintes[modifier | modifier le code]
Contrainte normale pour une poutre droite[modifier | modifier le code]

Plaçons-nous dans le cas d'un moment fléchissant Mfz positif ; dans le plan (Gxy), les fibres sont concentriques, le centre O est situé vers le haut. La longueur de l'arc est proportionnelle au rayon, c'est-à-dire qu'elle varie linéairement en fonction de l'abscisse y considérée. De même, la contrainte normale à la section varie linéairement en fonction de y et l'on trouve :
- .
où IGz est le moment quadratique d'axe (Gz), calculé en fonction de la forme de la section droite.
Le risque de rupture se situe sur la face en extension de la poutre. Si l'on appelle -V l'ordonnée du point situé sur cette face, la contrainte y vaut :
- .
La grandeur IGz/V est appelée « module de flexion élastique » et est noté Wél. z :
- .
Si la poutre est symétrique et de hauteur h, on a
Si l'on retient comme limite le fait que la matière doit rester dans le domaine élastique, on a à la limite
où Re est la limite d'élasticité. Le moment fléchissant maximal limite est alors
- .
Ceci sera utilisé pour comparer avec la flexion plastique.
- Note
- Comme c'est la valeur absolue de la contrainte qui nous intéresse, et que de toute manière le signe dépend de la convention choisie, on trouve souvent l'expression
Contrainte normale pour une poutre courbe[modifier | modifier le code]
Nous supposons que la poutre est générée par une courbe plane, dans le plan (x, y), et que la fibre neutre reste dans ce plan au cours de la déformation. C'est le cas typique d'un crochet de levage. Le rayon de courbure local (au repos) est noté r(x).
Comme dans le cas de la poutre droite, sous l'effet du moment fléchissant, les sections droites tournent, les fibres sont étirées ou comprimées. Mais contrairement au cas précédent, les fibres n'ont pas la même longueur initiale. La répartition de la contrainte selon y n'est plus linéaire, mais hyperbolique, de la forme[1] :
- .
Cisaillement[modifier | modifier le code]


Dans la plupart des cas, le moment fléchissant s'accompagne d'un effort tranchant (Ty avec Mfz, Tz avec Mfy). Cela génère de la cission (τxy pour Ty et τxz pour Tz). Cette contrainte de cisaillement ne génère que peu de risque de rupture et est donc généralement négligée (modèle de Bernoulli).
La répartition des contraintes n'est pas uniforme : la contrainte sur une surface libre est nécessairement dans le plan de la surface, donc la cission sur les faces extérieure est nulle. On a donc une cission qui croît lorsque l'on s'approche de la fibre neutre. La contrainte maximale vaut alors, si S est l'aire de la section droite :
- poutre de section rectangulaire pleine : ;
- poutre de section circulaire pleine : ;
- tube circulaire mince : ;
où S est l'aire de la section droite. On voit que sur ces exemples là, la contrainte est 1,5 à 2 fois supérieure au cas du cisaillement simple.
On note que la cission est maximale là où la contrainte normale est nulle (à la fibre neutre), et que la contrainte normale est maximale là ou la cission est nulle (sur les faces externes). On n'a donc pas de synergie entre les deux contraintes.
Calcul de la déformée[modifier | modifier le code]
Nous avons vu ci-dessus que :
- la déformation par cisaillement est négligée ;
- la courbure γ et le rayon de courbure ρ sont déterminés en fonction du moment fléchissant Mfz, du facteur de forme IGz et du module de Young E :
- ;
- la déformée uy est reliée à ρ et à γ selon l'équation différentielle :
- .
On peut donc déterminer la déformée par intégration double :
- .
Si la poutre est de section uniforme (IGz ne varie pas) de même matériau (E ne varie pas), on se contente d'intégrer le moment fléchissant :
où A et B sont des constantes d'intégration déterminées à partir des conditions limites :
- aux points de liaison, on a uy = 0 ;
- aux points d'encastrement, on a u’y = 0 ;
- si le problème est symétrique par rapport à la section droite médiane, on a u’y = 0 au centre de la poutre.
On s'intéresse en général à la valeur maximale de uy, la « flèche » de la poutre, qui détermine l'état limite en service (ELS, valeur de chargement à ne pas dépasser pour que la forme de la poutre reste compatible avec sa fonction).
- Note
- On trouve souvent la notation abusive
- EIGzy ’’ = Mfz.
- y désignant alors le déplacement.
- Par ailleurs, les expressions exactes sont :
- et donc
- .
La déformée peut être établie graphiquement par la méthode du funiculaire.
Flexion en grande déformation[modifier | modifier le code]

Lorsque le rayon de courbure ρ est inférieur à dix fois la hauteur h de la section
- ρ < h*10,
les hypothèses ne sont plus valables. Si toutefois on considère que :
- les sections droites restent planes ;
- les contraintes normales à la section sont indépendantes des contraintes parallèles à la section ;
alors la contrainte normale résultant du moment fléchissant devient
où S est l'aire de la section.
Flexion déviée[modifier | modifier le code]
La flexion déviée est le cas où les charges ne font pas pivoter la section autour d'un axe principal de moment quadratique; il existe toujours au moins deux axes principaux de moment quadratique quelle que soit la section de la poutre.
Poutre symétrique[modifier | modifier le code]

Dans le cas d'une poutre symétrique, on peut décomposer le vecteur moment de flexion en deux composantes Mfy et Mfz non nulles. Si l'on reste en petites déformations, le système est linéaire, on peut donc considérer que l'on a une superposition de deux flexions planes. La contrainte normale vaut donc
- .
Le plan sur lequel la contrainte s'annule est appelé « plan neutre ».
Poutre non symétrique[modifier | modifier le code]
On détermine les axes principaux d'inertie Y et Z (voir l'article Moment d'inertie), puis l'on se ramène au cas précédent en se plaçant dans le repère (GxYZ) :
- .
Cas isostatiques[modifier | modifier le code]
Flexion trois points[modifier | modifier le code]

La flexion trois points est un essai mécanique classique. Il représente le cas d'une poutre posée sur deux appuis simples (appuis linéaires rectilignes qui, dans un problème plan, équivalent à une liaison ponctuelle) et soumise à une charge concentrée, appliquée au milieu de la poutre avec elle aussi un contact simple. On modélise souvent un des appuis comme un pivot afin d'avoir une poutre qui ne se déplace pas horizontalement.
Dans la figure ci-contre, la poutre a une longueur L et la charge centrale est P.
L'effort tranchant est constant en valeur absolue : il vaut la moitié de la charge centrale, P/2. Il change de signe au milieu de la poutre. Le moment fléchissant varie de manière linéaire entre une extrémité, où il vaut 0, et le centre où sa valeur absolue vaut PL/4 ; c'est là que le risque de rupture est le plus important.
Le profil de la poutre est décrit par un polynôme du troisième degré (fonction en x3) sur une moitié de poutre (l'autre moitié étant symétrique).
Les diagrammes des efforts tranchants et moments fléchissants sont traditionnellement représentés remplis de traits verticaux. Cela correspond au découpage des aires en trapèze utilisé pour la méthode graphique.
Poutre sur deux appuis avec une charge ponctuelle[modifier | modifier le code]

Ce cas est la généralisation de la flexion trois points : la charge n'est pas nécessairement appliquée au centre. Cela permet, par exemple, de représenter une charge roulante.
L'analyse entre une extrémité et le point d'application de la charge est la même que pour la flexion trois points, mais le problème n'est plus symétrique.
Poutre encastrée[modifier | modifier le code]
Une poutre encastrée (clamped beam, cantilever), ou poutre en console, représente le cas d'une hampe de drapeau, d'un poteau scellé dans le sol, d'une poutre en porte à faux (par exemple une potence).
On peut remarquer qu'elle se comporte comme la moitié d'une poutre en flexion trois points, l'encastrement correspondant au centre. Le moment fléchissant maximal est au niveau de l'encastrement, c'est là que le risque de rupture est le plus important.
Flexion quatre points[modifier | modifier le code]
La différence principale avec la flexion trois points se situe entre les deux charges : le moment fléchissant est constant et l'effort tranchant est nul. Cette situation est qualifiée de flexion pure ou flexion circulaire.
Poutre sur deux appuis avec une charge répartie uniforme[modifier | modifier le code]
Une charge uniforme permet de décrire le poids propre de la poutre, ou encore le poids d'un liquide dans le cas d'une canalisation ou d'un réservoir.
Poutre sur deux appuis avec une charge répartie linéairement[modifier | modifier le code]
Ce cas peut servir à décrire la charge sur un poteau soutenant un mur vertical ayant d'un côté de la terre ou de l'eau : la pression augmente avec la profondeur.
Méthode graphique[modifier | modifier le code]
La résolution des problèmes de flexion isostatiques peut se faire graphiquement.
Cas hyperstatiques[modifier | modifier le code]
Poutre appuyée et encastrée (degré 1)[modifier | modifier le code]
Le cas d'une poutre appuyée et encastrée, par symétrie, est parfaitement identique au cas d'une poutre sur trois appuis à travées identiques (à l'appui, la pente est nulle et correspond à un encastrement).
Poutre sur trois appuis(degré 1)[modifier | modifier le code]
Dans le cas d'une poutre à deux travées identiques de longueur l, sous une charge uniforme q, le moment sur appui est identique au moment en travée d'une poutre simple, à savoir ; on ne gagne donc rien en termes de résistance à lier en continuité deux poutres sur un appui commun. Par contre le moment maximal en travée vaut et la flèche maximale est réduite d'environ 40 % par rapport à la poutre isostatique.
Poutre bi-encastrée (degré 3)[modifier | modifier le code]
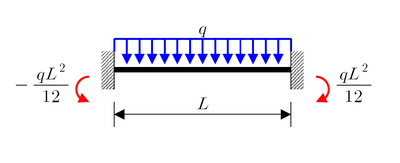 Charge continue uniformément répartie q |
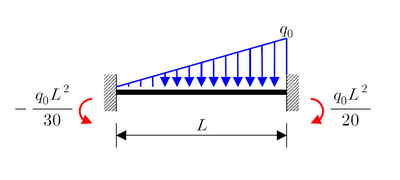 Charge triangulaire avec un maximum de q0 |
 Charge concentrée P |
 Couple M0 |
Flexion plastique[modifier | modifier le code]


Initialement, on retient comme critère de résistance (état limite ultime, ELU) le fait que la matière doit rester dans le domaine élastique. La charge maximale admise doit donc être telle que
- σmax ≤ Rpe
avec
- Rpe = Re/s : la résistance pratique à l'extension ;
- Re : la limite d'élasticité, typiquement de 185 à 355 MPa pour un acier de construction (acier non allié à basse teneur en carbone) ;
- s : coefficient de sécurité, typiquement entre 1,5 et 5.
On a donc des structures volontairement surdimensionnées, ce qui permet de faire face à des surcharges accidentelles.
Si l'on admet que certaines zones de la poutre peuvent se plastifier (subir de la déformation plastique), on peut dimensionner plus petit, donc concevoir une structure plus légère.
L'approche généralement retenue consiste à :
- considérer que la limite d'élasticité est la valeur maximale de la contrainte, ce qui revient à simplifier la courbe de traction ;
- prendre pour critère de ruine le moment où la totalité d'une section subit de la déformation plastique.
Lorsque la section est entièrement plastifiée, la contrainte normale vaut :
- -h/2 ≤ y < 0 : σ(y ) = Re ;
- 0 < y ≤ h/2 : σ(y ) = -Re.
Le moment fléchissant vaut
- .
Si la poutre est symétrique, alors
où Wpl est le module de flexion plastique :
- .
Notons que l'on a
- Wpl = 2Sz
où Sz est le moment statique de la demie section.
Par rapport à la flexion élastique, on accepte donc que la poutre subisse un moment fléchissant plus élevé. Le rapport φ entre ces deux moments est appelé « gain » et vaut :
- .
C'est un facteur de forme : il ne dépend que de la forme de la section droite.
| Profil | Gain |
|---|---|
| IPN | 1,18 |
| IPE | 1,15 |
| HEA | 1,15 |
| HEB | 1,16 |
| UPN | 1,19 |
| UAP | 1,18 |
| tube | 1,27 |
| plat | 1,5 |
| rond | 1,7 |
Lorsque la matière rentre dans le domaine plastique, il est nécessaire de faire intervenir la notion de rotule plastique, qui caractérise la plastification locale de la poutre. Le mécanisme de ruine de la structure peut alors être déterminé en utilisant le théorème cinématique ou le théorème statique de la mécanique des structures.
Cas d'une plaque[modifier | modifier le code]
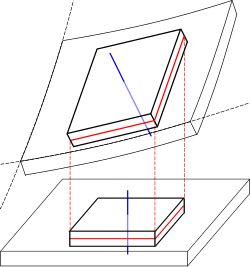
Dans la théorie des plaques, on considère
- des feuillets, c'est-à-dire de fines tranches de matières parallèles aux faces de la plaque, le feuillet moyen étant situé au milieu de la plaque, et
- des fibres normales, c'est-à-dire de fins tubes de matière perpendiculaires au feuillet moyen.

Dans la théorie des plaques minces de Kirchhoff-Love, le feuillet moyen se courbe mais n'est pas étiré dans son plan (pas de déformation de « membrane »), et les fibres normales restent perpendiculaires au feuillet moyen au cours de la déformation. On peut donc exprimer simplement les déplacements u et v d'un point selon respectivement x et y en fonction de l'altitude z de ce point, de son déplacement w selon z et des angles θx et θy :
- u(x, y, z) ≃ z·θy(x, y) ;
- v(x, y, z) ≃ -z·θx(x, y) ;
Dans l'absolu, l'hypothèse d'absence de déformation de membrane n'est valable que si la surface peut être développée, c'est-à-dire si elle n'a qu'une seule courbure (cylindre ou cône de révolution). Dans le cas général (voir les exemples de la sphère et de la selle de cheval), il y a nécessairement une étirement. L'hypothèse n'est donc valable que si le déplacement w est faible devant l'épaisseur h de la plaque.
Déformation[modifier | modifier le code]
D'après la définition du tenseur des déformations, on a :
où γx est la courbure du feuillet moyen dans le plan xz et γy dans le plan yz.
Efforts de cohésion[modifier | modifier le code]

Les moments fléchissants mxy, agissant sur la face normale à x et dont le vecteur est dirigé selon y, et myx, agissant sur la face normale à y et dont le vecteur est dirigé selon x, créent une répartition linéaire de la contrainte normale. Cette situation est similaire à celle de la poutre.
Contraintes[modifier | modifier le code]
On peut évaluer les contraintes à partir de la loi de Hooke :
soit
où E est le module de Young et ν est le coefficient de Poisson.
On peut relier les contraintes normales aux moments fléchissants par le principe d'équivalence ; il faut pour cela choisir une convention, à l'instar des conventions des efforts à gauche ou à droite pour les poutres. Ici, nous choisissons de noter les moments positifs s'ils provoquent une courbure vers le bas, c'est-à-dire si la face supérieure est en compression (σii < 0 pour z > 0) et la face inférieure est en traction (σii > 0 pour z < 0).
Donc, si l'élément de matière fait dx × dy × h, alors
soit
- .
Le terme
est appelé rigidité flexionnelle. Il joue le même rôle que le facteur E⋅IGz pour la flexion d'une poutre.
Comme on a
on en déduit les équations différentielles :
- .
Dans le cas général, mxy myx sont des fonctions de x et de y.
Cas particuliers[modifier | modifier le code]
Distribution uniforme de moments sur les côtés d'une plaque rectangulaire[modifier | modifier le code]

Nous allons d'abord nous placer dans le cas simple d'une plaque rectangulaire soumise à des moments uniformes à ses bords ; ce cas ne correspond pas à un cas réel particulièrement intéressant, mais permet d'avoir un certain nombre de résultats de manière simple. Cette situation est similaire à la flexion pure d'une poutre (partie centrale de la flexion à quatre points).
Dans notre cas particulier, on est dans le cas de torseurs couples. Si l'on considère un élément de matière n'importe où dans la plaque, on a donc :
- mxy = Mx ;
- myx = My.
Ce sont des constantes, on a donc
Dans ce cas-là, la solution est simple : on obtient des courbures uniformes :
avec
- .
Si l'un des couples extérieurs est nul, par exemple My = 0, alors on a
- γy = -νγx,
c'est-à-dire que les deux courbures principales sont opposées (courbe « anticlastique » de type selle de cheval). Dans le cas particulier où My = νMx, on a
- γy = 0
c'est-à-dire que l'on n'a qu'une courbure que dans un sens. Ce cas est similaire à la flexion pure d'une poutre, mais le résultat est légèrement différent :
Le facteur de différence 1/(1-ν²) provient du fait que la plaque n'a pas la possibilité de s'étendre librement sur les côtés. Dans le cas des métaux (ν ≃ 0,3), on a un écart d'environ 10 % (1/(1-ν²) ≃ 1,10).
Si l'on a My = Mx, alors
- γy = γx,
la plaque prend donc la forme d'une calotte de sphère. Ceci est en fait vrai quelle que soit la forme de la plaque, pour toute répartition uniforme des moments.
Pression uniforme[modifier | modifier le code]
- Plaque carrée appuyée
Dans le cas d'une plaque carrée de côté a simplement appuyée chargée par une pression uniforme p0, la flèche maximale wmax est au centre et vaut :
- .
- Plaque circulaire encastrée
Dans le cas d'une plaque circulaire de rayon R encastrée, la flèche à une distance r du centre vaut
- ;
la flèche maximale est au centre et vaut
- .
Notons que l'on peut également écrire la flèche sous la forme
- .
Application à la construction[modifier | modifier le code]

Comme il a été vu précédemment, les contraintes (et les déformations) dues à la flexion dans un élément (poutre ou plancher) sont principalement concentrées à proximité des fibres inférieure et supérieure, tandis que celles à proximité de la fibre neutre sont très peu sollicitées. Il est ainsi possible, pour des questions d'économie de matériaux, dans un but financier ou pour réduire le poids propre de l'élément, de concentrer la matière à distance de la fibre neutre et de l'amincir en son centre. C'est la raison pour laquelle on utilise des sections profilées en forme de tubes, de profilés laminés (en U, en I, en H, en cornières), des dalles nervurées ou à caisson, …
Notes et références[modifier | modifier le code]
- Michel Del Pedro, Thomas Gmür et John Botsis, « Flexion des poutres courbes », dans Introduction à la mécanique des solides et des structures, Lausanne, Presses polytechniques et universitaires romandes, (ISBN 2-88074-617-5), p. 115-124
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Jean-Louis Fanchon, Guide de mécanique, Nathan, , 543 p. (ISBN 2-09-178965-8), p. 265-396
- Claude Hazard, Frédy Lelong et Bruno Quinzain, Mémotech — Structures métalliques, Paris, Casteilla, , 352 p. (ISBN 2-7135-1751-6), p. 326-336
- D. Spenlé et R. Gourhant, Guide du calcul en mécanique : maîtriser la performance des systèmes industriels, Paris, Hachette, , 272 p. (ISBN 2-01-168835-3), p. 130-208


















































![{\displaystyle {\begin{matrix}\theta _{x}={\frac {\partial w}{\partial y}}{\text{ ;}}\\[1ex]\theta _{y}=-{\frac {\partial w}{\partial x}}{\text{.}}\\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79b39ec9a56e869640996c648395ca18c8eb37e9)
![{\displaystyle \left\{{\begin{array}{l}\varepsilon _{11}=z\cdot {\frac {\partial \theta _{y}}{\partial x}}=-z\cdot \gamma _{x}\\[1ex]\varepsilon _{22}=-z\cdot {\frac {\partial \theta _{x}}{\partial y}}=-z\cdot \gamma _{y}\\[1ex]\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55a6a46cd665d425662987fb30ce667db234e774)
![{\displaystyle \left\{{\begin{matrix}\varepsilon _{11}={\dfrac {1}{\mathrm {E} }}\cdot (\sigma _{11}-\nu \cdot \sigma _{22})\\[2ex]\varepsilon _{22}={\dfrac {1}{\mathrm {E} }}\cdot (\sigma _{22}-\nu \cdot \sigma _{11})\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01095a9651b10af6f365a8cbcf92fa49b38a63fc)
![{\displaystyle \left\{{\begin{matrix}\sigma _{11}=-{\dfrac {\mathrm {E} }{1-\nu ^{2}}}\cdot (\gamma _{x}+\nu \gamma _{y})\cdot z\\[2ex]\sigma _{22}=-{\dfrac {\mathrm {E} }{1-\nu ^{2}}}\cdot (\gamma _{y}+\nu \gamma _{x})\cdot z\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d696a74c5735789534ea03f1e2a1676e9754d735)
![{\displaystyle \left\{{\begin{matrix}m_{xy}\cdot \mathrm {d} y=\int _{-h/2}^{h/2}\left(\sigma _{11}\cdot z\cdot \mathrm {d} y\right)\cdot \mathrm {d} z\\[1ex]m_{yx}\cdot \mathrm {d} x=\int _{-h/2}^{h/2}\left(\sigma _{22}\cdot z\cdot \mathrm {d} x\right)\cdot \mathrm {d} z\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7473fd9052bb723772106aa0c6c8cc7d534c1b01)


![{\displaystyle \left\{{\begin{matrix}\gamma _{x}\simeq {\dfrac {\partial ^{2}w}{\partial x^{2}}}\\[2ex]\gamma _{y}\simeq {\dfrac {\partial ^{2}w}{\partial y^{2}}}\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c8d32780fc6ed2e9dae589ab3231cf0a511eaec)
![{\displaystyle \left\{{\begin{matrix}m_{xy}=-\mathrm {D} \cdot \left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu {\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\[1ex]m_{yx}=-\mathrm {D} \cdot \left({\frac {\partial ^{2}w}{\partial y^{2}}}+\nu {\frac {\partial ^{2}w}{\partial x^{2}}}\right)\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bae035a11cc5244f316334f5f6c7de1437002d97)

![{\displaystyle \left\{{\begin{matrix}\gamma _{x}=-{\dfrac {\mathrm {M} _{x}-\nu \mathrm {M} _{y}}{\mathrm {D} '}}\\[2ex]\gamma _{y}=-{\dfrac {\mathrm {M} _{y}-\nu \mathrm {M} _{x}}{\mathrm {D} '}}\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fdf7d91ea40e657d38dc52774f925f0e66bd307)





