Constante de Khintchine

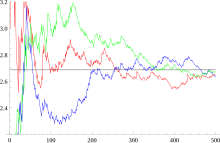
En théorie des nombres, la constante de Khintchine est la valeur de la moyenne géométrique que prennent l'infinité des dénominateurs du développement de la fraction continue d'un nombre réel, qui est identique pour presque tous les nombres réels. C'est un résultat démontré par Alexandre Iakovlevitch Khintchine.

Il est donc presque toujours vrai que, pour

$x = a_0 + \frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a_3 + ...}}} \in \R;$

on a

$\lim_{n \rightarrow \infty } \left( \prod_{i=1}^n a_i \right) ^{1/n} = K = \prod_{r=1}^\infty {\left\{ 1+{1\over r(r+2)}\right\}}^{\log_2 r} \approx 2,6854520010\dots$

Parmi les nombres x qui ont des développements en fractions continuées qui n'ont pas cette propriété se trouvent les nombres rationnels, les solutions des équations quadratiques à coefficients rationnels (incluant le nombre d'or $\varphi\,$), et la base des logarithmes naturels e.

Parmi les nombres qui ont des développements en fraction continue semblant avoir cette propriété (d'après des études numériques) sont $\pi\,$, $\gamma\,$ (la constante d'Euler-Mascheroni), et la constante de Khintchine elle-même. Néanmoins ces énoncés ne sont pas démontrés. En effet, bien que presque tous les nombres réels possèdent cette propriété, elle n'a été démontrée pour aucun nombre réel particulier.

On ne sait pas si la constante de Khintchine est irrationnelle.

Voir aussi

• Constante de Lévy