En mathématiques , la moyenne d'ordre p d'une famille de réels positifs, éventuellement pondérés, est une généralisation des moyennes arithmétique , géométrique et harmonique . Elle est également dite moyenne de Hölder , à cause de son lien avec la norme d'ordre p , ou norme de Hölder.
Soit p un nombre réel non nul. On définit la moyenne d'ordre p des réels strictement positifs x 1 , ... , xn
M
p
(
x
1
,
…
,
x
n
)
=
(
1
n
∑
i
=
1
n
x
i
p
)
1
p
{\displaystyle M_{p}(x_{1},\dots ,x_{n})=\left({\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{p}\right)^{\frac {1}{p}}}
Pour p = 0, on la pose comme étant la moyenne géométrique (ce qui correspond au cas limite de la moyenne d'ordre p lorsque p tend vers 0) :
M
0
(
x
1
,
…
,
x
n
)
=
∏
i
=
1
n
x
i
n
{\displaystyle M_{0}(x_{1},\dots ,x_{n})={\sqrt[{n}]{\prod _{i=1}^{n}x_{i}}}}
Les exposants infinis positif et négatif correspondent respectivement au maximum et au minimum, dans les cas classique et pondéré (ce qui correspond également au cas limite des moyennes d'ordres approchant de l'infini) :
M
∞
(
x
1
,
…
,
x
n
)
=
max
(
x
1
,
…
,
x
n
)
M
−
∞
(
x
1
,
…
,
x
n
)
=
min
(
x
1
,
…
,
x
n
)
{\displaystyle {\begin{aligned}M_{\infty }(x_{1},\dots ,x_{n})&=\max(x_{1},\dots ,x_{n})\\M_{-\infty }(x_{1},\dots ,x_{n})&=\min(x_{1},\dots ,x_{n})\end{aligned}}}
On peut également définir les moyennes pondérées d'ordre p pour une suite de poids positifs mi vérifiant
∑
m
i
=
1
{\displaystyle \sum m_{i}=1}
[ 1]
M
p
(
x
1
,
…
,
x
n
)
=
(
∑
i
=
1
n
m
i
x
i
p
)
1
p
M
0
(
x
1
,
…
,
x
n
)
=
∏
i
=
1
n
x
i
m
i
{\displaystyle {\begin{aligned}M_{p}(x_{1},\dots ,x_{n})&=\left(\sum _{i=1}^{n}m_{i}x_{i}^{p}\right)^{\frac {1}{p}}\\M_{0}(x_{1},\dots ,x_{n})&=\prod _{i=1}^{n}x_{i}^{m_{i}}\end{aligned}}}
Le cas classique correspond à l'équirépartition des poids : mi = 1/n
On remarquera le lien avec la norme d'ordre p :
M
p
(
x
1
,
⋯
,
x
n
)
=
1
n
1
/
p
‖
(
x
1
,
⋯
,
x
n
)
‖
p
{\displaystyle M_{p}(x_{1},\cdots ,x_{n})={\frac {1}{n^{1/p}}}\lVert (x_{1},\cdots ,x_{n})\rVert _{p}}
Comme la plupart des moyennes, la moyenne d'ordre p est une fonction homogène de degré 1 en x 1 , ... , xn b est un réel strictement positif, la moyenne généralisée d'ordre p des nombres bx 1 , ... , bxn b multiplié par la moyenne généralisée des x 1 , ... , xn
Comme les moyennes quasi-arithmétiques , le calcul de la moyenne peut être séparé en sous-blocs de même taille.
M
p
(
x
1
,
…
,
x
n
⋅
k
)
=
M
p
(
M
p
(
x
1
,
…
,
x
k
)
,
M
p
(
x
k
+
1
,
…
,
x
2
⋅
k
)
,
…
,
M
p
(
x
(
n
−
1
)
⋅
k
+
1
,
…
,
x
n
⋅
k
)
)
{\displaystyle M_{p}(x_{1},\dots ,x_{n\cdot k})=M_{p}(M_{p}(x_{1},\dots ,x_{k}),M_{p}(x_{k+1},\dots ,x_{2\cdot k}),\dots ,M_{p}(x_{(n-1)\cdot k+1},\dots ,x_{n\cdot k}))}
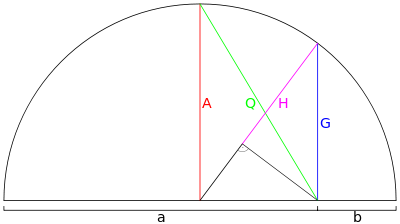
Visualisation des moyennes dans le cas n = 2 (moyennes de deux valeurs a et b ) : A est la moyenne arithmétique, Q la moyenne quadratique, G la moyenne géométrique, et H la moyenne harmonique.
M
−
∞
(
x
1
,
…
,
x
n
)
=
lim
p
→
−
∞
M
p
(
x
1
,
…
,
x
n
)
=
min
{
x
1
,
…
,
x
n
}
{\displaystyle M_{-\infty }(x_{1},\dots ,x_{n})=\lim _{p\to -\infty }M_{p}(x_{1},\dots ,x_{n})=\min\{x_{1},\dots ,x_{n}\}}
minimum
M
−
1
(
x
1
,
…
,
x
n
)
=
n
1
x
1
+
⋯
+
1
x
n
{\displaystyle M_{-1}(x_{1},\dots ,x_{n})={\frac {n}{{\frac {1}{x_{1}}}+\dots +{\frac {1}{x_{n}}}}}}
moyenne harmonique
M
0
(
x
1
,
…
,
x
n
)
=
lim
p
→
0
M
p
(
x
1
,
…
,
x
n
)
=
x
1
⋅
⋯
⋅
x
n
n
{\displaystyle M_{0}(x_{1},\dots ,x_{n})=\lim _{p\to 0}M_{p}(x_{1},\dots ,x_{n})={\sqrt[{n}]{x_{1}\cdot \dots \cdot x_{n}}}}
moyenne géométrique
M
1
(
x
1
,
…
,
x
n
)
=
x
1
+
⋯
+
x
n
n
{\displaystyle M_{1}(x_{1},\dots ,x_{n})={\frac {x_{1}+\dots +x_{n}}{n}}}
moyenne arithmétique
M
2
(
x
1
,
…
,
x
n
)
=
x
1
2
+
⋯
+
x
n
2
n
{\displaystyle M_{2}(x_{1},\dots ,x_{n})={\sqrt {\frac {x_{1}^{2}+\dots +x_{n}^{2}}{n}}}}
moyenne quadratique
M
+
∞
(
x
1
,
…
,
x
n
)
=
lim
p
→
∞
M
p
(
x
1
,
…
,
x
n
)
=
max
{
x
1
,
…
,
x
n
}
{\displaystyle M_{+\infty }(x_{1},\dots ,x_{n})=\lim _{p\to \infty }M_{p}(x_{1},\dots ,x_{n})=\max\{x_{1},\dots ,x_{n}\}}
maximum
De plus
M
1
/
2
(
a
,
b
)
=
(
a
+
b
2
)
2
=
M
0
(
a
,
b
)
+
M
1
(
a
,
b
)
2
{\displaystyle M_{1/2}(a,b)=\left({\frac {{\sqrt {a}}+{\sqrt {b}}}{2}}\right)^{2}={\frac {M_{0}(a,b)+M_{1}(a,b)}{2}}}
Preuve que
lim
p
→
0
M
p
=
M
0
{\displaystyle \textstyle \lim _{p\to 0}M_{p}=M_{0}}
(moyenne géométrique)
On réécrit la définition de Mp avec la fonction exponentielle
M
p
(
x
1
,
…
,
x
n
)
=
exp
(
ln
[
(
∑
i
=
1
n
m
i
x
i
p
)
1
/
p
]
)
=
exp
(
1
p
ln
(
∑
i
=
1
n
m
i
x
i
p
)
)
{\displaystyle M_{p}(x_{1},\dots ,x_{n})=\exp {\left(\ln {\left[\left(\sum _{i=1}^{n}m_{i}x_{i}^{p}\right)^{1/p}\right]}\right)}=\exp {\left({\frac {1}{p}}\ln \left(\sum _{i=1}^{n}m_{i}x_{i}^{p}\right)\right)}}
Pour p → 0, on applique la règle de L'Hôpital :
lim
p
→
0
1
p
ln
(
∑
i
=
1
n
m
i
x
i
p
)
=
lim
p
→
0
∑
i
=
1
n
m
i
x
i
p
ln
x
i
∑
i
=
1
n
m
i
x
i
p
=
∑
i
=
1
n
m
i
ln
x
i
=
ln
(
∏
i
=
1
n
x
i
m
i
)
{\displaystyle \lim _{p\to 0}{\frac {1}{p}}\ln \left(\sum _{i=1}^{n}m_{i}x_{i}^{p}\right)=\lim _{p\to 0}{\frac {\sum _{i=1}^{n}m_{i}x_{i}^{p}\ln {x_{i}}}{\sum _{i=1}^{n}m_{i}x_{i}^{p}}}=\sum _{i=1}^{n}m_{i}\ln {x_{i}}=\ln {\left(\prod _{i=1}^{n}x_{i}^{m_{i}}\right)}}
Par continuité de la fonction exponentielle, on obtient
lim
p
→
0
M
p
(
x
1
,
…
,
x
n
)
=
exp
(
ln
(
∏
i
=
1
n
x
i
m
i
)
)
=
∏
i
=
1
n
x
i
m
i
=
M
0
(
x
1
,
…
,
x
n
)
.
{\displaystyle \lim _{p\to 0}M_{p}(x_{1},\dots ,x_{n})=\exp {\left(\ln {\left(\prod _{i=1}^{n}x_{i}^{m_{i}}\right)}\right)}=\prod _{i=1}^{n}x_{i}^{m_{i}}=M_{0}(x_{1},\dots ,x_{n}).}
Preuve que
lim
p
→
∞
M
p
=
M
∞
{\displaystyle \textstyle \lim _{p\to \infty }M_{p}=M_{\infty }}
et
lim
p
→
−
∞
M
p
=
M
−
∞
{\displaystyle \textstyle \lim _{p\to -\infty }M_{p}=M_{-\infty }}
On suppose, quitte à réordonner les termes, que x 1 ≥ ... ≥ xn
lim
p
→
∞
M
p
(
x
1
,
…
,
x
n
)
=
lim
p
→
∞
(
∑
i
=
1
n
m
i
x
i
p
)
1
/
p
=
x
1
lim
p
→
∞
(
∑
i
=
1
n
w
i
(
x
i
x
1
)
p
)
1
/
p
=
x
1
=
M
∞
(
x
1
,
…
,
x
n
)
.
{\displaystyle \lim _{p\to \infty }M_{p}(x_{1},\dots ,x_{n})=\lim _{p\to \infty }\left(\sum _{i=1}^{n}m_{i}x_{i}^{p}\right)^{1/p}=x_{1}\lim _{p\to \infty }\left(\sum _{i=1}^{n}w_{i}\left({\frac {x_{i}}{x_{1}}}\right)^{p}\right)^{1/p}=x_{1}=M_{\infty }(x_{1},\dots ,x_{n}).}
Pour M -∞
M
−
∞
(
x
1
,
…
,
x
n
)
=
1
M
∞
(
1
/
x
1
,
…
,
1
/
x
n
)
.
{\displaystyle M_{-\infty }(x_{1},\dots ,x_{n})={\frac {1}{M_{\infty }(1/x_{1},\dots ,1/x_{n})}}.}
En général, on a
si p < q , alors
M
p
(
x
1
,
…
,
x
n
)
⩽
M
q
(
x
1
,
…
,
x
n
)
{\displaystyle M_{p}(x_{1},\dots ,x_{n})\leqslant M_{q}(x_{1},\dots ,x_{n})}
et il y a égalité si et seulement si x 1 = x 2 = ... = xn .
L'inégalité est vraie pour les valeurs réelles de p et q , ainsi que pour les infinis positif et négatif.
On en déduit que pour tout réel p ,
∂
∂
p
M
p
(
x
1
,
…
,
x
n
)
⩾
0
{\displaystyle {\frac {\partial }{\partial p}}M_{p}(x_{1},\dots ,x_{n})\geqslant 0}
ce qui peut être montré en utilisant l'inégalité de Jensen .
En particulier, pour p dans {−1, 0, 1}, l'inégalité des moyennes généralisées implique une inégalité sur les moyennes pythagoriciennes ainsi que l'inégalité arithmético-géométrique .
On travaillera ici sur les moyennes généralisées pondérées, et on supposera :
m
i
∈
[
0
;
1
]
∑
i
=
1
n
m
i
=
1
{\displaystyle {\begin{aligned}m_{i}\in [0;1]\\\sum _{i=1}^{n}m_{i}=1\end{aligned}}}
La preuve sur les moyennes généralisées s'obtiendra en prenant mi = 1/n
Équivalence des inégalités entre les moyennes de signes opposés [ modifier | modifier le code ] Supposons qu'une inégalité entre les moyennes généralisées d'ordre p et q soit vraie :
∑
i
=
1
n
m
i
x
i
p
p
≥
∑
i
=
1
n
m
i
x
i
q
q
{\displaystyle {\sqrt[{p}]{\sum _{i=1}^{n}m_{i}x_{i}^{p}}}\geq {\sqrt[{q}]{\sum _{i=1}^{n}m_{i}x_{i}^{q}}}}
Alors en particulier :
∑
i
=
1
n
m
i
x
i
p
p
≥
∑
i
=
1
n
m
i
x
i
q
q
{\displaystyle {\sqrt[{p}]{\sum _{i=1}^{n}{\frac {m_{i}}{x_{i}^{p}}}}}\geq {\sqrt[{q}]{\sum _{i=1}^{n}{\frac {m_{i}}{x_{i}^{q}}}}}}
On prend l'inverse des nombres, ce qui change le sens de l'inégalité car les xi sont positifs :
∑
i
=
1
n
m
i
x
i
−
p
−
p
=
1
∑
i
=
1
n
m
i
1
x
i
p
p
≤
1
∑
i
=
1
n
m
i
1
x
i
q
q
=
∑
i
=
1
n
m
i
x
i
−
q
−
q
{\displaystyle {\sqrt[{-p}]{\sum _{i=1}^{n}m_{i}x_{i}^{-p}}}={\sqrt[{p}]{\frac {1}{\sum _{i=1}^{n}m_{i}{\frac {1}{x_{i}^{p}}}}}}\leq {\sqrt[{q}]{\frac {1}{\sum _{i=1}^{n}m_{i}{\frac {1}{x_{i}^{q}}}}}}={\sqrt[{-q}]{\sum _{i=1}^{n}m_{i}x_{i}^{-q}}}}
ce qui donne le résultat pour les moyennes généralisées d'ordre −p et −q . On peut faire le calcul réciproque, montrant ainsi l'équivalence des inégalités, ce qui sera utile par la suite.
Pour tout q > 0, on a
∑
i
=
1
n
m
i
x
i
−
q
−
q
⩽
∏
i
=
1
n
x
i
m
i
⩽
∑
i
=
1
n
m
i
x
i
q
q
{\displaystyle {\sqrt[{-q}]{\sum _{i=1}^{n}m_{i}x_{i}^{-q}}}\leqslant \prod _{i=1}^{n}x_{i}^{m_{i}}\leqslant {\sqrt[{q}]{\sum _{i=1}^{n}m_{i}x_{i}^{q}}}}
Démonstration
Par l'inégalité de Jensen appliquée à la fonction logarithme, qui est concave :
ln
(
∏
i
=
1
n
x
i
m
i
)
=
∑
i
=
1
n
m
i
ln
(
x
i
)
⩽
ln
(
∑
i
=
1
n
m
i
x
i
)
{\displaystyle \ln \left(\prod _{i=1}^{n}x_{i}^{m_{i}}\right)=\sum _{i=1}^{n}m_{i}\ln(x_{i})\leqslant \ln \left(\sum _{i=1}^{n}m_{i}x_{i}\right)}
En passant à l'exponentielle, on obtient
∏
i
=
1
n
x
i
m
i
⩽
∑
i
=
1
n
m
i
x
i
{\displaystyle \prod _{i=1}^{n}x_{i}^{m_{i}}\leqslant \sum _{i=1}^{n}m_{i}x_{i}}
et en prenant les puissances q -ièmes des xi , on obtient le résultat voulu pour l'inégalité avec q positif. Le cas négatif se traite de façon similaire.
Il reste à prouver que si p < q , alors on a :
∑
i
=
1
n
m
i
x
i
p
p
⩽
∑
i
=
1
n
m
i
x
i
q
q
{\displaystyle {\sqrt[{p}]{\sum _{i=1}^{n}m_{i}x_{i}^{p}}}\leqslant {\sqrt[{q}]{\sum _{i=1}^{n}m_{i}x_{i}^{q}}}}
Si p est négatif et q positif, on peut utiliser le résultat précédent :
∑
i
=
1
n
m
i
x
i
p
p
⩽
∏
i
=
1
n
x
i
m
i
⩽
∑
i
=
1
n
m
i
x
i
q
q
{\displaystyle {\sqrt[{p}]{\sum _{i=1}^{n}m_{i}x_{i}^{p}}}\leqslant \prod _{i=1}^{n}x_{i}^{m_{i}}\leqslant {\sqrt[{q}]{\sum _{i=1}^{n}m_{i}x_{i}^{q}}}}
Supposons maintenant p et q positifs. On définit la fonction f : R + → R +
f
(
x
)
=
x
q
p
{\displaystyle f(x)=x^{\frac {q}{p}}}
f est une fonction puissance , deux fois dérivable :
f
″
(
x
)
=
(
q
p
)
(
q
p
−
1
)
x
q
p
−
2
{\displaystyle f''(x)=\left({\frac {q}{p}}\right)\left({\frac {q}{p}}-1\right)x^{{\frac {q}{p}}-2}}
qui est positive sur le domaine de définition de f , car q > p , ainsi f est convexe.
Par l'inégalité de Jensen , on a :
f
(
∑
i
=
1
n
m
i
x
i
p
)
⩽
∑
i
=
1
n
m
i
f
(
x
i
p
)
{\displaystyle f\left(\sum _{i=1}^{n}m_{i}x_{i}^{p}\right)\leqslant \sum _{i=1}^{n}m_{i}f(x_{i}^{p})}
soit:
∑
i
=
1
n
m
i
x
i
p
p
q
≤
∑
i
=
1
n
m
i
x
i
q
{\displaystyle {\sqrt[{\frac {p}{q}}]{\sum _{i=1}^{n}m_{i}x_{i}^{p}}}\leq \sum _{i=1}^{n}m_{i}x_{i}^{q}}
ce qui, une fois élevé à la puissance 1/q (fonction croissante, car 1/q est positif), on obtient le résultat voulu.
Le cas de p et q négatifs se tire de ce résultat, en les remplaçant respectivement par −q et −p .
La moyenne d'ordre p peut être vue comme un cas particulier des moyennes quasi-arithmétiques :
M
f
(
x
1
,
…
,
x
n
)
=
f
−
1
(
1
n
⋅
∑
i
=
1
n
f
(
x
i
)
)
{\displaystyle M_{f}(x_{1},\dots ,x_{n})=f^{-1}\left({{\frac {1}{n}}\cdot \sum _{i=1}^{n}{f(x_{i})}}\right)}
Par exemple, la moyenne géométrique s'obtient par f (x ) = ln(x )p avec f (x ) = xp
Une moyenne d'ordre p sert de moyenne glissante non linéaire car elle fait ressortir les petites valeurs pour p petit et amplifie les grandes valeurs pour p grand.
↑ J. Lelong-Ferrand et J.M. Arnaudiès , Cours de mathématiques tome 2 : Analyse , Dunod université, 1977 , p. 586
Exhaustives
Partielles
Résultats


![{\displaystyle M_{0}(x_{1},\dots ,x_{n})={\sqrt[{n}]{\prod _{i=1}^{n}x_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c389840696d51db570f6af4e5443feb30ff1a4a)







![{\displaystyle M_{0}(x_{1},\dots ,x_{n})=\lim _{p\to 0}M_{p}(x_{1},\dots ,x_{n})={\sqrt[{n}]{x_{1}\cdot \dots \cdot x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61bc811b24285b8134ca93a3cbefde3c13262b6f)





![{\displaystyle M_{p}(x_{1},\dots ,x_{n})=\exp {\left(\ln {\left[\left(\sum _{i=1}^{n}m_{i}x_{i}^{p}\right)^{1/p}\right]}\right)}=\exp {\left({\frac {1}{p}}\ln \left(\sum _{i=1}^{n}m_{i}x_{i}^{p}\right)\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ded3721c94b53591a822ea4aef6753fbba3e4c)








![{\displaystyle {\begin{aligned}m_{i}\in [0;1]\\\sum _{i=1}^{n}m_{i}=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87d9da21499cbde642f8c1dbf7e472dc3610c1b1)
![{\displaystyle {\sqrt[{p}]{\sum _{i=1}^{n}m_{i}x_{i}^{p}}}\geq {\sqrt[{q}]{\sum _{i=1}^{n}m_{i}x_{i}^{q}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bded30cd6ae74b0086bd9cba740cf5ac88eeb289)
![{\displaystyle {\sqrt[{p}]{\sum _{i=1}^{n}{\frac {m_{i}}{x_{i}^{p}}}}}\geq {\sqrt[{q}]{\sum _{i=1}^{n}{\frac {m_{i}}{x_{i}^{q}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4178e87f069e713557f7f09f015a757be61b2e7)
![{\displaystyle {\sqrt[{-p}]{\sum _{i=1}^{n}m_{i}x_{i}^{-p}}}={\sqrt[{p}]{\frac {1}{\sum _{i=1}^{n}m_{i}{\frac {1}{x_{i}^{p}}}}}}\leq {\sqrt[{q}]{\frac {1}{\sum _{i=1}^{n}m_{i}{\frac {1}{x_{i}^{q}}}}}}={\sqrt[{-q}]{\sum _{i=1}^{n}m_{i}x_{i}^{-q}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4a42e2972f16faa723299ae1daa160fbbe58ccc)
![{\displaystyle {\sqrt[{-q}]{\sum _{i=1}^{n}m_{i}x_{i}^{-q}}}\leqslant \prod _{i=1}^{n}x_{i}^{m_{i}}\leqslant {\sqrt[{q}]{\sum _{i=1}^{n}m_{i}x_{i}^{q}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26e018e383accc8ed2b093953e86fc24e1cea5da)


![{\displaystyle {\sqrt[{p}]{\sum _{i=1}^{n}m_{i}x_{i}^{p}}}\leqslant {\sqrt[{q}]{\sum _{i=1}^{n}m_{i}x_{i}^{q}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a7ac89ac8fe2e2001d5db9502883e367f4203dc)
![{\displaystyle {\sqrt[{p}]{\sum _{i=1}^{n}m_{i}x_{i}^{p}}}\leqslant \prod _{i=1}^{n}x_{i}^{m_{i}}\leqslant {\sqrt[{q}]{\sum _{i=1}^{n}m_{i}x_{i}^{q}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/911f41ecd129031c9a75e28626c0e64e580844fc)



![{\displaystyle {\sqrt[{\frac {p}{q}}]{\sum _{i=1}^{n}m_{i}x_{i}^{p}}}\leq \sum _{i=1}^{n}m_{i}x_{i}^{q}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec427d1da08ed1ee206d3072b3d949e76009087)
