Mesure de probabilité

Dans de nombreux cas, la physique statistique utilise des mesures de probabilité, mais toutes les mesures qu'elle utilise ne sont pas des mesures de probabilité.

En mathématiques, une mesure de probabilité est une fonction à valeurs réelles définie sur un ensemble d'événements dans un espace de probabilité qui satisfait les propriétés de mesure telles que la $\sigma$-additivité. La différence entre une mesure de probabilité et la notion plus générale de mesure (qui inclut des concepts tels que l'aire ou le volume) est qu'une mesure de probabilité doit attribuer la valeur 1 à tout l'espace de probabilité.

Intuitivement, la propriété d'additivité dit que la probabilité attribuée à l'union de deux événements disjoints par la mesure devrait être la somme des probabilités des événements, par exemple la valeur attribuée à "1 ou 2" dans un lancer de dé devrait être la somme des valeurs affectées à "1" et "2".

Les mesures de probabilité ont des applications dans divers domaines, de la physique à la finance ou à la biologie.

Définition

Une mesure de probabilité associant l'espace de probabilité pour 3 événements à l'intervalle unité .

Les conditions pour qu'une fonction μ soit une mesure de probabilité sur un espace de probabilité sont les suivantes :

• μ doit retourner des résultats dans l'intervalle unité [0, 1], retournant 0 pour l'espace vide et 1 pour l'espace entier.

• μ doit satisfaire la propriété de $\sigma$-additivité, c'est-à-dire, pour toute collection dénombrable $\{E_{i}\}$ d'ensembles disjoints deux à deux, on a :

$\mu {\Bigl (}\bigcup _{i\in I}E_{i}{\Bigr )}=\sum _{i\in I}\mu (E_{i}).$

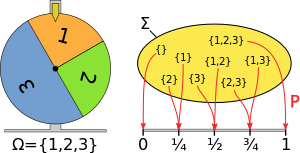
Par exemple, étant donné trois éléments 1, 2 et 3 avec des probabilités 1/4, 1/4 et 1/2, la valeur attribuée à {1, 3} est 1/4 + 1/2 = 3/4, comme dans le schéma à droite.

La probabilité conditionnelle fondée sur l'intersection d'événements définie par :

$\mu (B\mid A)={\frac {\mu (A\cap B)}{\mu (A)}}.$

satisfait aux conditions de mesure de probabilité tant que $\mu (A)$ n'est pas nulle.

Les mesures de probabilité sont distinctes de la notion plus générale de mesures floues dans laquelle il n'est pas nécessaire que les valeurs floues totalisent 1, et la propriété d'additivité est remplacée par une relation d'ordre fondée sur l'inclusion d'ensemble.

Exemples d'applications

Les mesures de marché qui attribuent des probabilités aux espaces des marchés financiers sur la base des mouvements réels du marché sont des exemples de mesures de probabilité qui présentent un intérêt pour la finance mathématique, par exemple dans la tarification des dérivés financiers. Par exemple, une mesure neutre au risque est une mesure de probabilité qui suppose que la valeur actuelle des actifs est la valeur attendue du gain futur pris par rapport à cette même mesure neutre au risque (c'est-à-dire calculée à l'aide de la fonction de densité neutre au risque correspondante), et actualisé au taux sans risque. S'il existe une mesure de probabilité unique qui doit être utilisée pour évaluer les actifs sur un marché, alors le marché est appelé un marché complet.

Toutes les mesures qui représentent intuitivement le hasard ou la probabilité ne sont pas des mesures de probabilité. Par exemple, bien que le concept fondamental d'un système en mécanique statistique soit un espace de mesure, ces mesures ne sont pas toujours des mesures de probabilité. En général, en physique statistique, si l'on considère des phrases de la forme "la probabilité d'un système S supposant que l'état A est p", la géométrie du système ne conduit pas toujours à la définition d'une mesure de probabilité sous congruence, bien qu'elle puisse le faire donc dans le cas de systèmes avec un seul degré de liberté.

Les mesures de probabilité sont également utilisées en biologie mathématique. Par exemple, dans l'analyse comparative de séquence, une mesure de probabilité peut être définie pour la probabilité qu'un variant puisse être autorisé pour un acide aminé dans une séquence.

Articles connexes

• Mesure Borel
• Mesure de Haar
• Mesure de Lebesgue

Bibliographie

• Patrick Billingsley, Probability and Measure, John Wiley, 1995, 608 p. (ISBN 0-471-00710-2)
• Robert B. Ash et Catherine A. Doléans-Dade, Probability & Measure Theory, Academic Press, 1999 (ISBN 0-12-065202-1)