Équilibre liquide-vapeur
L'équilibre liquide-vapeur est un état dans lequel un liquide et sa vapeur (phase gazeuse) sont en équilibre, c'est-à-dire qu'il y a autant de vaporisation (transformation du liquide au gaz) que de liquéfaction (transformation du gaz au liquide) à l'échelle moléculaire. À l'échelle macromoléculaire on n'observe donc aucun changement dans le temps. Un corps pur à l'équilibre liquide-vapeur est généralement qualifié de fluide saturé.
Pour un composé chimique pur, cela implique qu'il est à son point d'ébullition[1]. La notion de « fluide saturé » inclut le liquide saturé (sur le point de se vaporiser), le mélange liquide-vapeur saturé et la vapeur saturée (sur le point de se liquéfier).
Introduction[modifier | modifier le code]
À l'équilibre liquide-vapeur, un mélange liquide aura une vapeur d'équilibre dont la composition (concentrations ou pressions partielles des gaz) dépend de la composition du liquide (concentration de chaque composé dans le liquide) et de la température. L'inverse est aussi vrai : si un mélange de vapeurs est en équilibre avec sa phase liquide, alors la composition du liquide sera déterminée par la composition des vapeurs et la température. Ces données de l'équilibre liquide-vapeur peuvent être déterminées expérimentalement, ou calculées approximativement grâce à des modèles comme la loi de Raoult, la loi de Dalton et la loi de Henry.
Ces données sont primordiales dans la construction de colonnes de distillation, tout particulièrement la distillation fractionnée, spécialité du génie chimique[2],[3],[4]. La distillation est un procédé utilisé pour séparer (totalement ou partiellement) les composés d'un mélange en portant à ébullition (vaporisation) puis en refroidissant (liquéfaction) le mélange. Elle se base sur la différence de concentration des composés entre la phase liquide et la phase gazeuse.
Dans les mélanges contenant au moins deux composés, les concentrations sont souvent exprimées en fractions molaires. La fraction molaire d'un composé dans une phase (liquide ou gaz) est le nombre de moles (ou quantité) de ce composé dans la phase divisé par le nombre de total de moles de tous les composés dans cette même phase.
Les mélanges contenant deux composés sont dits binaires, ceux contenant trois composés sont dits ternaires. Les données de l'équilibre liquide-vapeur existent évidemment avec davantage de composés, mais elles sont complexes à représenter graphiquement. Ces données sont fonction de la pression totale.
Quand on atteint la température à laquelle la somme des pressions de vapeur des composés liquides est égale à la pression totale (la somme ne peut être qu'inférieure ou égale), alors des bulles de vapeur sont générées et le mélange bout. Cette température est le point d'ébullition du mélange à pression donnée. Le point d'ébullition à la pression de 1 atm est appelé point d'ébullition normal du mélange.
Description thermodynamique[modifier | modifier le code]
La thermodynamique permet de déterminer si l'équilibre liquide-vapeur est possible, ainsi que de décrire ses propriétés. L'analyse dépend de la nature du système : s'il est pur ou non.
Corps pur[modifier | modifier le code]
Pour un corps pur l'état d'équilibre entre les deux phases liquide et vapeur est décrit par les équations suivantes :
- (équilibre mécanique)
- (équilibre thermique)
- (équilibre chimique)
avec :
- et les pressions du liquide et de la vapeur ;
- et les températures du liquide et de la vapeur ;
- et les potentiels chimiques respectivement dans le liquide et la vapeur[5].
Autrement dit, la température, la pression et l'enthalpie libre molaire sont les mêmes entre les deux phases, lorsqu'elles sont à l'équilibre. La pression d'un corps pur gazeux en équilibre avec sa phase liquide est appelée pression de vapeur saturante du corps pur, elle dépend fortement de la température.
Un moyen plus commun d'exprimer la condition d'équilibre liquide-vapeur dans un système pur est d'utiliser le concept de fugacité ; l'égalité des potentiels chimiques est remplacée par l'égalité :
où et sont les fugacités respectivement du liquide et de la vapeur à la température et à la pression [5]. L'utilisation de la fugacité est souvent plus pratique pour les calculs, sachant que la fugacité du liquide est, pour une erreur acceptable, indépendante de la pression[5] et il est aussi souvent pratique d'utiliser , le coefficient de fugacité (sans dimension), égal à 1 pour un gaz parfait.
Systèmes avec plusieurs composés[modifier | modifier le code]
Pour les systèmes composés de plusieurs espèces chimiques, l'état d'équilibre entre les deux phases est décrit par les équations :
- pour chacun des composés du système
avec :
- et les pressions du liquide et de la vapeur ;
- et les températures du liquide et de la vapeur ;
- et les potentiels chimiques du corps respectivement dans le liquide et la vapeur.
Coefficient de partage et volatilité relative[modifier | modifier le code]

La tendance d'une espèce chimique donnée à se déplacer préférentiellement vers une phase (liquide ou gaz) est caractérisée par le coefficient de partage [6]. Il existe des données d'équilibre liquide-vapeur pour des mélanges de quatre composés ou plus, mais de tels diagrammes sont complexes à représenter. Pour de tels systèmes, ainsi que pour les mélanges binaires, l'équilibre est donc représenté par les valeurs de [2],[3] définies par :
où et sont les fractions molaires du composé , respectivement dans les phases gaz et liquide.
Pour les mélanges binaires (ne contenant que deux constituants), le rapport des constantes des deux composés est appelé volatilité relative (en), notée :
Elle quantifie la facilité ou la difficulté de séparer deux composés. La distillation à grande échelle industrielle est rarement mise en place si la volatilité relative est inférieure à 1,05, lorsque le composé le plus volatil est , et le composé le moins volatil [3].
Les valeurs de sont largement utilisées pour les calculs déterminant le design des colonnes de distillation continue pour les mélanges.
Loi de Raoult[modifier | modifier le code]
À la température d'ébullition, et à des températures supérieures, la somme des pressions partielles de chaque constituant est égale à la pression totale, notée . Dans ces conditions, la loi de Dalton donne :
Ainsi, pour chaque composant la fraction molaire en phase vapeur vaut :
où est la pression partielle du composé .
La loi de Raoult établit, pour chacun des composés d'un mélange, la relation :
avec :
- la pression de vapeur du composé pur ;
- la fraction molaire du composé dans la phase liquide.
La combinaison des deux lois donne pour chaque composant :
La loi de Raoult est approximativement valable pour des mélanges dont les composés présentent peu d'interactions entre eux, tels les mélanges d'alcanes, composés apolaires et relativement inertes.
Mélanges réels[modifier | modifier le code]
Pour des solutions réelles, dans lesquelles les interactions entre composants différents ne sont pas identiques, on écrit :
avec :
- , température d'équilibre ;
- , pression d'équilibre ;
- , pression de vapeur saturante du corps pur à ;
- , coefficient de fugacité du corps en phase vapeur, à , et composition du mélange gazeux ;
- , coefficient de fugacité du corps pur à saturation en phase vapeur, à et ;
- , coefficient d'activité du corps en phase liquide, à , et composition du mélange liquide ;
- , volume molaire liquide du corps pur à ;
- , correction de Poynting.
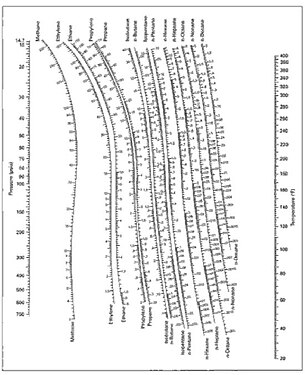
Les valeurs de la constante sont empiriquement et théoriquement corrélées à la température, à la pression et à la composition des phases sous formes d'équations, de tables ou de graphiques, comme ceux de DePriester[7].
Diagrammes d'équilibre liquide-vapeur d'un mélange[modifier | modifier le code]
Diagramme carré[modifier | modifier le code]

Pour chaque composé d'un mélange binaire (composé de deux espèces chimiques notées 1 et 2) il est possible de tracer la fonction dans un diagramme carré représentant la fraction molaire liquide du corps 1 selon les abscisses (axe horizontal) et la fraction molaire gazeuse du même corps selon les ordonnées (axe vertical). Les fractions molaires gazeuses et du corps 2 sont liées à celles du corps 1 par les relations :
Il est donc possible de représenter les quatre fractions molaires comme sur le diagramme donné en exemple sur la figure 1[3]. La diagonale entre les coins de coordonnées (, ) et (, ) est utilisée comme référence. Si la courbe d'équilibre croise la diagonale, le point d'intersection représente un azéotrope.
Ce type de diagramme est utilisé dans la méthode de McCabe et Thiele pour déterminer le nombre d'étages d'équilibre (ou plateaux théoriques (en)) nécessaires pour distiller un mélange binaire donné en une fraction distillée et une fraction restante. Des corrections peuvent être effectuées afin de prendre en compte l'efficacité incomplète de chaque plateau de la colonne de distillation quand on les compare aux théoriques.
Les diagrammes carrés sont tracés à température ou pression donnée.
Diagramme de phases binaires[modifier | modifier le code]

Il est possible de tracer, à pression ou température donnée, respectivement la température ou la pression de changement de phase en fonction de la composition d'un mélange binaire. La figure 2 présente un exemple de diagramme à pression donnée donnant la température de changement de phase en fonction de la composition d'un corps noté 1.
Pour toute température où les deux phases sont présentes, une certaine fraction molaire de vapeur est en équilibre avec une certaine fraction molaire de liquide, et celles-ci sont souvent différentes. Elles sont représentées par deux points sur la même isotherme (droite horizontale du diagramme). Ainsi, quand une série de températures est représentée en fonction des fractions molaires de vapeur et de liquide, on obtient deux courbes. La plus basse, représentant la température d'ébullition du mélange en fonction de la fraction molaire du corps 1 liquide, est appelée courbe du point de bulle. La plus haute, représentant le point de rosée du mélange en fonction de la fraction molaire du corps 1 vapeur, est appelée courbe du point de rosée[2].
Ces deux courbes se rejoignent aux deux extrémités, c'est-à-dire lorsque le composé 1 est pur (, soit ), et lorsque le composé 2 est pur (, soit ). Les températures en ces deux points correspondent aux températures d'ébullition des deux composés purs à la pression du diagramme.
Sur la figure 2 le mélange binaire entièrement gazeux se trouve au-dessus de la courbe du point de rosée, le mélange entièrement liquide sous la courbe du point de bulle et l'équilibre liquide-vapeur entre les deux courbes. Pour une température donnée, la fraction molaire du corps 1 vapeur se lit à l'intersection de la droite isotherme horizontale correspondante et de la courbe du point de rosée, la fraction molaire du corps 1 liquide se lit à l'intersection de la droite isotherme et de la courbe du point de bulle.
Pour certains couples de substances, les deux courbes coïncident aussi en un point entre et auquel le liquide et la vapeur ont la même composition. Ce point particulier est appelé azéotrope pour ce couple de substances. Il est caractérisé par une température azéotrope et une composition azéotropique (souvent exprimée en fraction molaire) à la pression du diagramme. Il existe des azéotropes d'ébullition maximale, où la température azéotrope est à un maximum de la courbe d'ébullition, ainsi que des azéotropes d'ébullition minimale, où la température azéotrope est à un minimum de la courbe d'ébullition.
Diagrammes ternaires[modifier | modifier le code]

Il est possible de représenter des mélanges ternaires sous forme de diagrammes tridimensionnels. Deux des dimensions sont utilisées pour représenter les fractions molaires, et la troisième est utilisée pour représenter la température.
Les fractions molaires des trois composés, notées , et , sont liées par la relation :
- .
En utilisant les deux premières dimensions, la composition peut être représentée par un triangle équilatéral, comme sur la figure 3, où chaque sommet représente un des composants pur. Les côtés du triangle représentent un mélange de deux des composants et chaque point à l'intérieur du triangle représente la composition du mélange des trois composés.
Le point d'ébullition et le point de rosée du mélange sont représentés par des surfaces courbes à l'intérieur d'un prisme dont le diagramme triangulaire précédent est la base. Les arêtes du prisme correspondent donc aux trois composants purs. Chaque face du prisme triangulaire représente un diagramme binaire du mélange binaire correspondant similaire à celui représenté sur la figure 2. La surface d'ébullition du mélange ternaire passe donc par les courbes de bulle des trois diagrammes binaires, et la surface de rosée du mélange ternaire passe donc par les courbes de rosée des trois diagrammes binaires
Cependant, à cause de leur complexité tridimensionnelle, ce type de diagramme est rarement représenté. Les surfaces courbes tridimensionnelles sont le plus souvent représentées sur des graphiques bidimensionnels à des intervalles gradués (comme sur des cartes où sont représentées les altitudes). Il faut donc deux graphiques : un pour les points d'ébullition et un autre pour les points de rosée.
Références[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Vapor–liquid equilibrium » (voir la liste des auteurs).
- Yunus A. Çengel et Michael A. Boles, Thermodynamics : an engineering approach, Boston, McGraw-Hill, coll. « mechanical engineering. », , 930 p. (ISBN 978-0-07-238332-4, 978-0-071-12177-4 et 978-0-072-45113-9), p. 65
- (en) Henry Z. Kister, Distillation Design, New York, McGraw-hill, , 1re éd., 710 p. (ISBN 0-07-034909-6 et 978-0-070-34909-4, OCLC 24142446)
- Perry, R.H. et Green, D.W. (Editors), Perry's Chemical Engineers' Handbook, McGraw-hill, , 7e éd. (ISBN 0-07-049841-5)
- Seader, J. D. et Henley, Ernest J., Separation Process Principles, New York, Wiley, (ISBN 0-471-58626-9).
- Balzhiser et al., Chemical Engineering Thermodynamics, (ISBN 0-13-128603-X), p. 215.
- (en) J M Smith, H C Van Ness et Michael M Abbott, Introduction to Chemical Engineering Thermodynamics, Boston, McGraw-Hill, , 7e éd., 817 p. (ISBN 978-0-07-310445-4, 978-0-071-24708-5 et 978-0-072-40296-4, OCLC 56491111).
- DePriester, C.L., Chem. Eng. Prog. Symposium Series, vol. 7:49, p. 1–43.