Escalier de Penrose
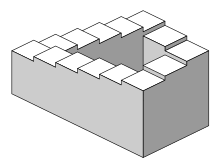
L'escalier de Penrose est un objet impossible prenant la forme d'un escalier. Il a été conçu en 1958 par le généticien britannique Lionel Penrose, en se basant sur le triangle de Penrose créé par son fils, le mathématicien et physicien Roger Penrose[1].
Description[modifier | modifier le code]
L'escalier de Penrose est une représentation en deux dimensions d'un escalier faisant quatre virages à angle droit, revenant ainsi à son point de départ ; selon la perception commune, les marches forment une boucle, constituant une perpétuelle montée (ou descente, selon le sens de rotation) ; en d'autres termes, il semble n'y avoir ni point le plus haut, ni point le plus bas.
Histoire[modifier | modifier le code]
Cette figure a été présentée en même temps que les autres objets impossibles créés par les Penrose, dans un article publié en 1958 dans le British Journal of Psychology[2].
L'artiste suédois Oscar Reutersvärd avait imaginé un escalier impossible plusieurs années avant les Penrose, mais ces derniers n'en avaient pas connaissance lorsqu'ils ont créé le leur[3].
En 1970, Richard Gregory a montré qu'on peut créer des objets qui, vus depuis un certain point, se dessinent en perspective ou se photographient comme le dessin de Penrose. Il classe le dessin parmi les perceptions paradoxales, et l'explique par l'absence de détails dans la représentation. En l'absence d'indices, nous supposons que les angles sont droits, que les marches sont horizontales, et que deux lignes proches se touchent, comme c'est le cas en général[4].
Analyse[modifier | modifier le code]
En 1983, Nicholas Falletta propose de découper l'escalier en tranches horizontales, pour analyser rationnellement l'illusion qu'il créée[5].
Un dessin en perspective représente sur une surface plane un objet en volume. Du point de vue mathématique et logique, une infinité d'objets à trois dimensions ont la même projection dans un espace à deux dimensions. La perception de la profondeur dans un dessin en perspective est donc nécessairement une interprétation, basée sur la connaissance préalable des objets[6],[7].
On peut réaliser des objets qui, observés depuis un point de vue précis, apparaissent exactement comme le dessin de Penrose[8],[9],[10],[11],[12].
Inspirations[modifier | modifier le code]
L'escalier de Penrose fut repris en 1960 par l'artiste M. C. Escher dans une de ses œuvres, Montée et Descente, dans laquelle l'escalier est intégré au toit d'un monastère dont les moines font pénitence en le gravissant et en le descendant sans fin. C'est d'ailleurs après avoir découvert des œuvres antérieures d'Escher que Roger Penrose s'en était inspiré pour créer ses objets impossibles, et notamment cet escalier avec son père.
En 1964, le psychologue Roger Shepard a créé une séquence sonore appelée gamme de Shepard dont les notes semblent paradoxalement monter sans fin. Dans son article présentant sa séquence sonore, Shepard fait le rapprochement avec l'escalier de Penrose et en reproduit un dessin[13] ; cette comparaison est reprise dans de nombreux articles sur la gamme de Shepard[14],[15],[16]. De plus, Shepard a dessiné en 1990 une adaptation de l'escalier de Penrose dans son ouvrage Mind Sights, dans lequel il indique également que l'escalier de Penrose lui a inspiré un dessin paradoxal intitulé Gradus ad Parnassum[17],[18].
La pochette de l'album Angles du groupe The Strokes reprend aussi cette figure[19].
Dans les œuvres de fiction[modifier | modifier le code]
Certaines œuvres de fiction utilisent un escalier de Penrose dans leur intrigue, exploitant ses propriétés uniques.
En 1986, dans le film Le Nom de la rose de Jean-Jacques Annaud, adaptation du roman éponyme d'Umberto Eco, l'escalier de Penrose est présent dans la bibliothèque labyrinthique de l'abbaye bénédictine.
En 2000, Andrea Camilleri a parlé de l'escalier de Penrose dans La Disparition de Judas avec un anachronisme, le livre se passant en 1890[20].
La figure a inspiré en 2006 à Goo-Shun Wang un court métrage d'animation intitulé Hallucii, dans lequel un homme ivre se retrouve piégé dans un escalier de Penrose[21].
Le paradoxe de l'escalier de Penrose est également mis en évidence en 1998 dans le film Chapeau melon et bottes de cuir[22].
On la trouve en 2010 dans le film Inception. Dans ce dernier, l'escalier permet d'échapper aux menaçantes projections des subconscients : en effet, étant un escalier complexe, le rêveur peut le passer car il en est le créateur, mais pas les projections, car elles ne s'attendent pas à cela.
Dans le clip Here I am de Tom Odell (2016), on trouve Kevin Spacey gravissant un escalier de Penrose infini[23],[24]
L'album Le Masque d'Horus de la série de bande dessinée Papyrus utilise un escalier de Penrose dans un temple secret. Si le lecteur reconnaît la forme, Papyrus lui-même ne se rend pas compte de l'anomalie en l'observant, mais une fois qu'il s'y engage, il constate à sa grande surprise qu'il est revenu au même point en ne faisant que descendre. Les prêtres du temple, eux, savent que l'escalier ne mène nulle part.
Dans un des gags de la bande dessinée Game Over, on peut voir le petit barbare coincé dans un escalier de Penrose. Il ne fait que monter, mais revient toujours au même point, ce qui déclenche le Game Over.
La bande dessinée Nabuchodinosaure reprend ce même principe, sous la forme d'une rivière que Nabucho essaie de descendre grâce à un tronc d'arbre.
Références[modifier | modifier le code]
- (en) Al Seckel (en) (préf. Douglas Hofstadter), Masters of Deception : Escher, Dalí & the Artists of Optical Illusion, New York, Sterling Publishing, , 320 p. (ISBN 1-4027-0577-8, lire en ligne), p. 83 [lire en ligne].
- (en) Lionel S. Penrose et Roger Penrose, « Impossible Objects : A Special Type of Illusion », British Journal of Psychology, vol. 49, no 1, , p. 31–33 (PMID 13536303, DOI 10.1111/j.2044-8295.1958.tb00634.x).
- (en) David Darling, The Universal Book of Mathematics : From Abracadabra to Zeno's Paradoxes, Hoboken, Wiley, , 383 p. (ISBN 0-471-27047-4), p. 238.
- (en) Richard Gregory, Seeing Through Illusions, Oxford University Press, , 253 p. (ISBN 978-0-19-280285-9), p. 232.
- (en) Nicholas Falletta, The Paradoxicon : A Collection of Contradictory Challenges, Problematical Puzzles and Impossible Illustrations, Garden City, Doubleday, , 230 p. (ISBN 0-385-17932-4), rééd. Wiley, New York, 1990 (ISBN 0-471-52950-8), p. 32, cité par (en) Marcel Danesi (en), The Puzzle Instinct : The Meaning of Puzzles in Human Life, Bloomington, Indiana University Press, , 269 p. (ISBN 0-253-34094-2), p. 81–82.
- Gregory 2009, p. 231.
- Richard Gregory (trad. de l'anglais par Micheline Mattheeuws-Hambrouck et Georges Thinès), L'œil et le cerveau : La psychologie de la vision [« Eye and Brain: The Psychology of Seeing »], Bruxelles/Paris, De Boeck Université, coll. « Neurosciences et Cognition », (1re éd. 1966), 335 p. (ISBN 2-7445-0067-4), « Voir la profondeur ».
- Photographies sous deux angles différents dans Philippe Comar, La perspective en jeu, Paris, Gallimard, coll. « Découvertes / Sciences » (no 138), , 128 p. (ISBN 2-07-053185-6).
- (en) IllusionWorks, « Impossible staircase », : exemple de modèle physique.
- (en) dorcuswang, « Illusion Staircase », , (en) braincollector, « Impossible Geometry », : vidéos sur YouTube mettant en évidence comment un tel modèle physique est possible.
- (en) Andrew Lipson, « Escher's "Ascending and Descending" in LEGO® » : exemple de reproduction en Lego de l'œuvre d'Escher.
- Vidéo d'un escalier sans fin à l'Institut de Technologie de Rochester, et son utilisation "bluffante".
- (en) Roger Shepard, « Circularity in Judgments of Relative Pitch », The Journal of the Acoustical Society of America, vol. 36, no 12, , p. 2346–2353 (DOI 10.1121/1.1919362).
- (en) Ben Carson, « Book Reviews : What Are Musical Paradox and Illusion? », American Journal of Psychology, vol. 120, no 1, , p. 123–140 (JSTOR 20445384, lire en ligne) : « An often-cited metaphor for Shepard’s illusion is the Penrose staircase » (p. 132).
- (en) Diana Deutsch, « The Paradox of Pitch Circularity », Acoustics Today, vol. 6, no 3, , p. 8 (DOI 10.1121/1.3488670, lire en ligne).
- (en) Baltasar Trancón y Widemann et Markus Lepper, « The Shepard Tone and Higher-Order Multi-rate Synchronous Data-Flow Programming in SIG », Proceedings of the 3rd ACM SIGPLAN International Workshop on Functional Art, Music, Modelling and Design (FARM 2015), New York, ACM, , p. 6–14 (ISBN 978-1-4503-3806-6, DOI 10.1145/2808083.2808086) : « The Shepard Tone [...] has been cited as the acoustic equivalent of Penrose's and Escher's impossible circular graphical configurations » (p. 8).
- (en) Ellen K. Levy, David E. Levy et Michael E. Goldberg, « Art and the Brain : The Influence of Art on Roger Shepard's Studies of Mental Rotation », Journal of the History of the Neurosciences: Basic and Clinical Perspectives, vol. 13, no 1, , p. 79-90 (DOI 10.1080/09647040490885510) : « Shepard's drawing labeled Figure 111-7 in Mind Sights (Fig. 7) of an “impossible” staircase is actually his re-drawn adaptation of the endless stairway illusion originally published by Penrose & Penrose. Shepard states (Shepard, 1990, pp. 92, 146-147) that an article about impossible objects written by L.S. Penrose first inspired his own anomaly drawing, “Gradus Ad Parnassum.” » (p. 85) et « Fig. 7. Shepards re-drawn adaptation of an endless stairway illusion, which relates to his “Gradus ad Parnassum (Drawing F3)” from Shepard, 1990, p. 148). This drawing deconstructs an “impossible” staircase derived from an earlier drawing by L.S. Penrose and R. Penrose. » (p. 87).
- (en) Roger Shepard, Mind Sights : Original Visual Illusions, Ambiguities, and Other Anomalies, With a Commentary on the Play of Mind in Perception and Art, New York, W. H. Freeman & Co., , 228 p. (ISBN 0-7167-2134-1 et 0-7167-2133-3), p. 92, 146–147.
- Jean-Marie Pottier, « Mon arrêt du cœur pour les Strokes », sur Slate, .
- La disparition de Judas éditions Métailé 2002 p.155
- (en) hallucii.com, site officiel du film.
- (en) Eric W. Weisstein, « Penrose Stairway », sur MathWorld.
- (en) Katie Baillie, « 5 new music videos that deserve a few minutes of your time », sur Metro.co.uk, .
- (en) Ferdinand Lehr, « Study of algorithmic generation of Penrose-Staircases », .
