Déformation élastique

En mécanique des milieux continus, une déformation élastique est une déformation réversible, c'est-à-dire qui disparaît lorsque les forces appliquées au matériau disparaissent. Elle est généralement linéaire (proportionnelle à la force appliquée).

Causes de l'élasticité[modifier | modifier le code]

Les raisons physiques du comportement élastique diffèrent d'un matériau à un autre. Pour les métaux, le treillis atomique change de taille et de forme quand des forces leur sont appliquées (ajout d'énergie au système). Quand les forces sont supprimées, le système retourne à son état original où l'énergie est la plus faible. Pour le caoutchouc et autres polymères, l'élasticité est due à l’extension des chaînes de polymère lorsque les forces sont appliquées. Dans les tissus biologiques élastiques (muscle par exemple), plusieurs de ces causes peuvent être mobilisées.

L'élasticité linéaire concerne les petites déformations proportionnelles à la sollicitation. Dans cette gamme, l'allongement est proportionnel à la force dans le cas d'un étirement, selon le module de Young, et l'angle est proportionnel au couple dans le cas d'une torsion, selon le module de Coulomb.

Aux plus grandes déformations, l'élasticité devient non linéaire pour certains matériaux.

La déformation élastique est un domaine important de la mécanique des milieux continus (MMC) et de la thermodynamique (compression des gaz).

Généralités[modifier | modifier le code]

Les matériaux peuvent être soumis à l'action d'une force qui les déforme. Tous les matériaux sont plus ou moins élastiques, c'est-à-dire qu'ils reviennent à leur forme primitive si la force appliquée n'a pas dépassé un certain seuil (la limite d'élasticité) et qu'elle cesse d'agir. Dans le cas contraire, il y a déformation plastique, voire rupture^[1].

Lorsqu'un corps est soumis à l'action de forces qui tendent à le comprimer ou à l'allonger, les raccourcissements ou les allongements sont entre certaines limites proportionnels aux forces qui les produisent, l'expérience — pour la première fois réalisée par le physicien anglais Robert Hooke — le prouve. Dans ce cas et si la force cesse d'agir, le corps reprend presque exactement sa forme et ses dimensions primitives. On dit alors que l'élasticité du corps n'a pas été altérée et l'allongement ou le raccourcissement observé qui a disparu, ou plutôt dont il ne reste qu'une trace insensible se nomme « déformation élastique ». L'expérience apprend aussi que lorsque les allongements ou les raccourcissements ne sont plus proportionnels aux forces, les corps ne reprennent plus leur forme et leurs dimensions primitives : lorsque ces forces ont cessé d'agir les corps demeurent plus ou moins allongés ou comprimés. On dit alors que leur élasticité est altérée, on parle de déformation plastique et la modification qui subsiste ultérieurement dans leurs dimensions se nomme « allongement permanent », « contraction permanente ». La durée d'action des forces exerce une grande influence sur les effets qui se produisent. Ainsi dans le cas où une force n'agira que momentanément, on pourra sans craindre d'altérer l'élasticité du corps, donner à cette force une puissance plus grande que celle que l'on pourrait employer si les efforts s'exerçaient d'une manière permanente^[1].

Il existe différents modules d'élasticité, tels que le module de Young, le module de rigidité ou de cisaillement et le module d'élasticité isostatique, qui sont tous des mesures des propriétés élastiques d'un matériau, en tant que résistance à la déformation sous une charge appliquée. Les différents modules s'appliquent à différents types de déformation. Le module de Young (par Thomas Young) s'applique à l'extension/compression d'un corps, alors que le module de cisaillement s'applique à son cisaillement^[2].

L'élasticité des matériaux est décrite par une courbe contrainte-déformation, qui montre la relation entre la contrainte (la force interne de restauration moyenne par unité de surface) et la déformation (la déformation relative)^[3]. La courbe est généralement non linéaire, mais elle peut être (approximativement linéaire) en utilisant des séries de Taylor pour des déformations suffisamment petites (dans lesquelles les termes d'ordre supérieur sont négligeables). Si le matériau est isotrope, la relation contrainte-déformation linéarisée est appelée loi de Hooke, qui est souvent présumée s'appliquer jusqu'à la limite d'élasticité pour la plupart des métaux ou des matériaux cristallins, alors qu'une élasticité non linéaire est généralement requise pour modéliser de grandes déformations de matériaux caoutchouteux élastiques. Pour des contraintes encore plus élevées, les matériaux présentent un comportement plastique, c'est-à-dire qu'ils se déforment irréversiblement et ne reviennent pas à leur forme d'origine, alors que la contrainte n'est plus appliquée^[4]. Pour les matériaux en caoutchouc tels que les élastomères, la pente de la courbe contrainte-déformation augmente avec la contrainte, ce qui signifie que les caoutchoucs deviennent progressivement plus difficiles à étirer, tandis que pour la plupart des métaux, le gradient diminue à des contraintes très élevées, ce qui les rend progressivement plus faciles étirer^[4]. L'élasticité n'est pas seulement applicable aux solides ; les fluides non newtoniens, tels que les fluides viscoélastiques, présentent également une élasticité, dans certaines conditions, quantifiées par le nombre de Deborah. En réponse à une petite contrainte, rapidement appliquée et retirée, ces fluides peuvent se déformer, puis revenir à leur forme originale. Sous des contraintes plus grandes, ou des contraintes appliquées pendant de plus longues périodes de temps, ces fluides peuvent commencer à s'écouler à la manière d'un liquide visqueux.

Élasticité linéaire[modifier | modifier le code]

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Valeurs particulières[modifier | modifier le code]

Module de Young[modifier | modifier le code]

Article détaillé : Module de Young.

Limite d'élasticité[modifier | modifier le code]

Article détaillé : Limite d'élasticité.

La déformation élastique intervient pour les faibles sollicitations. Si l'on augmente les sollicitations, on change le mode de déformation :

rupture (endommagement) pour les matériaux dits « fragiles » ;
déformation plastique (irréversible et non linéaire) puis rupture pour les matériaux dits « ductiles » ;
éventuellement fluage pour les matériaux ductiles si la vitesse de déformation est lente ou la température élevée.

La contrainte délimitant le domaine élastique des autres domaines est appelée limite d'élasticité (en anglais : yield strength).

Coefficient de Poisson[modifier | modifier le code]

Article détaillé : Coefficient de Poisson.

Contrainte et déformation[modifier | modifier le code]

On utilise deux modèles de déformation élastique : la traction-compression et le cisaillement. La flexion peut se modéliser selon les cas comme une traction-compression ou comme un cisaillement, la torsion se modélise comme un cisaillement (voir plus bas).

Traction-compression uniaxiale[modifier | modifier le code]

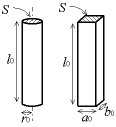
Prenons le cas de la traction ou de la compression d'une pièce cylindrique ou parallélépipédique selon son axe. La traction-compression correspond à des forces s'exerçant perpendiculairement aux sections de ces pièces ; elle est dite uniaxiale car les côtés de la pièce ne sont pas contraints, toutes les forces sont sur un même axe.

Allongement dans l'axe[modifier | modifier le code]

En prenant des pièces de différentes dimensions, on remarque que pour une force donnée :

l'allongement $Δ l$ est proportionnel à la longueur initiale $l 0$ du cylindre ;

ceci se conçoit bien : si l'on met deux ressorts identiques bout-à-bout, le premier ressort transmet intégralement la force au second ressort, les deux s'allongent donc de la même quantité ; donc si avec un ressort on a un allongement

Δ l 1

, avec deux ressorts l'allongement total est

2 Δ l 1

;

l'allongement $Δ l$ est inversement proportionnel à la section du cylindre ;

on conçoit également aisément que si l'on met deux ressorts identiques en parallèle, chaque ressort exercera la moitié de la force de traction, l'allongement final sera donc

Δ l 1 /2

; si l'on double la section de la pièce, c'est comme si l'on mettait deux pièces côte-à-côte.

Si l'on veut caractériser le matériau en faisant abstraction de la forme de la pièce et de ses dimensions, on définit donc :

l'allongement relatif ou déformation (en anglais : strain), noté $ε$

\varepsilon ={\frac {\Delta l}{l_{0}}}={\frac {l-l_{0}}{l_{0}}}

ε

est sans dimension, on l'exprime parfois en % (100×Δl/l₀)

la contrainte (en anglais : stress), notée $σ$

\sigma ={\frac {F}{S}}

σ

est homogène à une pression ; du fait des valeurs énormes mises en jeu, on l'exprime généralement en méga pascals (MPa).

La loi élastique s'écrit alors :

\sigma =E\varepsilon

,

c'est la loi de Hooke ; $E$ est le module de Young (en anglais : Young's modulus), qui est une caractéristique du matériau. $E$ est également homogène à une pression, du fait des valeurs très élevées qu'il prend, il est généralement exprimé en giga pascals (GPa).

On voit aisément que la densité d'énergie de déformation $w$ , c'est-à-dire l'énergie élastique divisée par le volume de la pièce, vaut :

w={\frac {1}{2}}\sigma \cdot \varepsilon ={\frac {1}{2}}E\varepsilon ^{2}

.

Lorsque l'on exerce une traction ou une compression, on constate que la largeur de la pièce varie également, à l'inverse de l'allongement. La variation relative de dimension est proportionnelle à l'allongement relatif $ε$ , le coefficient de proportionnalité s'appelle le coefficient de Poisson (en anglais : Poisson's ratio) en hommage au mathématicien français Siméon Denis Poisson. Il est noté $ν$ et est sans unité :

pour un cylindre :

{\frac {\Delta r}{r_{0}}}=-\nu \cdot {\frac {\Delta l}{l_{0}}}=-\nu \cdot \varepsilon

;

pour un parallélépipède rectangle :

{\frac {\Delta a}{a_{0}}}=-\nu \cdot {\frac {\Delta l}{l_{0}}}=-\nu \cdot \varepsilon

{\frac {\Delta b}{b_{0}}}=-\nu \cdot {\frac {\Delta l}{l_{0}}}=-\nu \cdot \varepsilon

.

On considère le volume de la pièce. Pour une pièce cylindrique, on a :

V=l\times \pi r^{2}

.

Pour des petites variations, on a donc :

{\frac {\Delta V}{V_{0}}}={\frac {\Delta l}{l_{0}}}+2{\frac {\Delta r}{r_{0}}}

(développement limité au premier ordre), soit :

{\frac {\Delta V}{V_{0}}}=(1-2\nu )\varepsilon

.

De même pour une pièce parallélépipédique, on a :

V=l\times a\times b

{\frac {\Delta V}{V_{0}}}={\frac {\Delta l}{l_{0}}}+{\frac {\Delta a}{a_{0}}}+{\frac {\Delta b}{b_{0}}}

donc de même :

{\frac {\Delta V}{V_{0}}}=(1-2\nu )\varepsilon

.

On voit donc que :

si

ν > 0,5

, le volume diminue en traction et augmente en compression (cas exceptionnel) ;

si

ν < 0,5

le volume augmente en traction et diminue en compression (comportement le plus général).

Pour un acier, $ν$ vaut environ 0,3, on est donc dans le second cas.

Si maintenant on maintient la largeur constante — par exemple on effectue une compression mais la pièce est dans une gaine ultra-rigide et ne peut pas s'étendre —, alors, la déformation n'est plus uniaxiale, la gaine exerce une pression (une contrainte) sur les côtés de la pièce. Il faut alors utiliser un autre coefficient élastique, noté $C 11$ , différent de $E$ :

\sigma =C_{11}\cdot \varepsilon

.

Cisaillement[modifier | modifier le code]

Si l'on considère un parallélépipède rectangle, le cisaillement est une variation de l'angle, qui n'est plus droit. Cela correspond à des forces s'exerçant parallèlement à la face.

On définit de même la contrainte comme étant la force divisée par la surface sur laquelle elle s'exerce ; cette contrainte est appelée cission (toujours exprimée en MPa) et est notée $τ$ .

La déformation est l'écart à l'angle droit $γ$ , appelé cisaillement. exprimé en radians.

On a toujours une loi linéaire :

\tau =G\gamma

où $G$ est le module de cisaillement ou module de Coulomb, généralement exprimé en GPa. Dans le cas d'un milieu isotrope, le module de cisaillement est lié au module de Young et au coefficient de Poisson par la relation suivante :

G={\frac {E}{2\;(1+\nu )}}

.

Note : dans l'article Tenseur des déformations, l'angle $γ$ défini vaut la moitié de l'angle $γ$ défini ici.

Compression isostatique[modifier | modifier le code]

Une compression isostatique est l'exercice d'une pression isotrope, c'est-à-dire qui a la même valeur dans toutes les directions. Si l'on désigne par $V$ le volume de l'objet, la variation de volume relative est proportionnelle à la variation de la pression $P$ :

\Delta P=-K\cdot {\frac {\Delta V}{V_{0}}}

où $K$ est le module d'élasticité à la compression isostatique^[5] (en anglais : bulk modulus). On remarque que $K$ est l'inverse du coefficient de compressibilité isotherme $χ T$ défini en thermodynamique par :

{\frac {1}{K}}=\chi _{T}=-{\frac {1}{V}}\cdot \left({\frac {\partial V}{\partial P}}\right)_{T}

$K$ est aussi homogène à une pression et est généralement exprimé en gigapascals (GPa). On a :

Matériau	K (GPa)
acier	160
eau	2,2
air	0,0001^[6]

Dans le cas d'un milieu isotrope, le module d'élasticité isostatique $K$ , le module de Young $E$ et le module de cisaillement $G$ sont liés par la relation suivante :

{\frac {1}{E}}={\frac {1}{9\;K}}+{\frac {1}{3\;G}}

.

Cas des grandes déformations[modifier | modifier le code]

La définition que l'on a prise de ε dépend du trajet suivi. On considère une déformation finale de ε₁ + ε₂. Si l'on fait la déformation en une étape, la longueur finale est :

l=l_{0}(1+\varepsilon _{1}+\varepsilon _{2})

.

Si par contre on déforme d'abord de $ε 1$ , on a une première longueur :

l=l_{0}(1+\varepsilon _{1})

qui devient la longueur initiale pour l'étape suivante, donc lorsque l'on rajoute une déformation $ε 2$ , on obtient :

l=l_{0}(1+\varepsilon _{1})(1+\varepsilon _{2})

.

En développant cette dernière formule, on voit que les deux sont équivalentes si :

\varepsilon _{1}\cdot \varepsilon _{2}<\!\!<\varepsilon _{1}\ \mathrm {et} \ \varepsilon _{1}\cdot \varepsilon _{2}<\!\!<\varepsilon _{2}

,

soit, de manière synthétique, si :

\varepsilon ^{2}<\!\!<\varepsilon \ \mathrm {soit} \ \varepsilon <\!\!<1

,

c'est l'hypothèse des petites déformations.

Pour les grandes déformations, on peut utiliser une autre définition de ε :

\varepsilon =\ln \left({\frac {l}{l_{0}}}\right)

,

on voit que si $l$ et $l 0$ sont proches, le développement limité de cette formule redonne la définition de $ε$ des petites déformations.

Pourquoi les lois sont-elles linéaires ?[modifier | modifier le code]

De manière générale, toute loi peut localement (c'est-à-dire pour de petites variations) se remplacer par un développement limité du premier ordre, ou « approximation linéaire », à condition que la tangente de la loi ne soit pas horizontale autour du point considéré. Les lois élastiques sont donc des approximations linéaires du comportement réel, plus complexe.

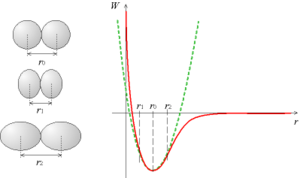
Plus précisément, l'explication de la linéarité se trouve dans la forme du potentiel interatomique $W (r)$ , où $r$ est la distance entre deux atomes.

À une température de 0 K, la distance entre deux atomes est $r 0$ . Si l'on s'éloigne un peu de cette valeur, l'énergie $W$ augmente ; on peut localement approcher la loi de $W$ par une parabole (il s'agit en fait d'un développement limité au second ordre), on peut donc écrire :

W(r)=W_{0}+k\cdot (r-r_{0})^{2}

.

La force étant la dérivée de l'énergie potentielle, on voit que les atomes sont soumis à une force de rappel (qui tend à faire revenir à $r 0$ ) qui vaut :

F=2k\cdot (r-r_{0})

qui est bien une loi linéaire.

Déformations complexes[modifier | modifier le code]

Jusqu'ici, des exemples de déformation très simples ont été montrés : traction uniaxiale, cisaillement, compression isostatique, sur un parallélépipède rectangle. Les applications réelles correspondent à des pièces et des sollicitations plus complexes, nécessitant de décrire la déformation et les contraintes par des matrices, des tenseurs, voir les articles :

Exemple des ressorts[modifier | modifier le code]

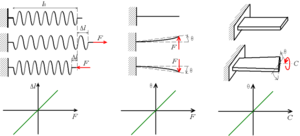
Le cas le plus simple de déformation élastique est celui des ressorts.

Sur les dessins, la réaction du support auquel est accroché le ressort n'est pas représentée. Mais il faut bien voir que la déformation résulte de l'application de deux actions mécaniques opposées (forces et/ou couples) ; s'il n'y a qu'une seule force, en application du principe fondamental de la dynamique, la force accélère le ressort sans provoquer de déformation, on se ramène à la mécanique du point.

Lorsque les lois de déformation sont linéaires, le coefficient de proportionnalité est appelé raideur du ressort et est noté $k$ :

$F = k 1 \cdot Δ l$ pour une traction-compression ;
$F = k 2 \cdot θ$ pour une flexion ;
$C = k 3 \cdot θ$ pour une torsion.

On remarque que les coefficients $k 1$ , $k 2$ et $k 3$ ne sont pas homogènes (ils n'ont pas la même dimension). L'angle $θ$ doit être exprimé en radians.

Dans le cas d'un ressort à spires non-jointives, l'énergie de déformation élastique $W$ est le travail de la force :

W=\int _{0}^{\Delta l}F\cdot dl

.

C'est donc la surface du triangle délimité par la droite dans le graphique $(Δ l, F)$ , soit :

W={\frac {1}{2}}k_{1}\Delta l_{2}={\frac {1}{2}}F\cdot \Delta l

.

Illustration graphique de l'énergie de déformation élastique dans le cas d'un ressort à spires non-jointives.

Note : sur la première figure, un graphique montrant la déformation en fonction de la force a été utilisé, par exemple $(F, Δ l)$ . Sur la deuxième figure, les axes sont inversés et la force est représentée en fonction de la déformation $(Δ l, F)$ . Si la première représentation semble plus intuitive (on se représente la force comme la cause de la déformation), les deux sont équivalentes. C'est de fait la seconde, $(Δ l, F)$ , qui est la plus utilisée, les essais de traction se faisant à déformation imposée croissante (voir l'explication dans l'article essais mécaniques).

Notes et références[modifier | modifier le code]

↑ ^{a et b} Eug Roffiaen, Traité théorique et pratique sur la résistance des matériaux dans les constructions, Félix Oudart, 1858.
↑ Landau L.D. et Lipshitz E.M., Theory of Elasticity, 3^e éd., 1970, 1-172.
↑ L. R. G. Treloar, The Physics of Rubber Elasticity, Oxford, Clarendon Press, 1975, 310 p. (ISBN 978-0-19-851355-1), p. 2.
↑ ^{a et b} Gijsbertus de With, Structure, Deformation, and Integrity of Materials, volume I : Fundamentals and Elasticity, Weinheim, Wiley VCH, 2006, 838 p. (ISBN 978-3-527-31426-3), p. 32.
↑ La notion de module de compressibilité est ambiguë puisqu'il s'agit de l'inverse de ladite « compressibilité ».
↑ L'équation des gaz parfaits donne χ_T = 1/P, soit K = P = 10⁵ Pa = 10⁻⁴ GPa à 1 atm.

Bibliographie[modifier | modifier le code]

Mekaouche, A., Chapelle, F. et Balandraud, X., Obtention de rigidité variable d'une structure robotique par l'utilisation d'un alliage à mémoire de forme, 2015, S07 Mécanique des structures.

Voir aussi[modifier | modifier le code]

Sur les autres projets Wikimedia :

Déformation élastique, sur Wikiversity

Articles connexes[modifier | modifier le code]

Liens externes[modifier | modifier le code]

Théorie de l'élasticité des corps solides, É. Mathieu (1835-1890), Traité de physique mathématique (sur Gallica).
Tenseurs contrainte/déformation - loi de comportement élastique isotrope, orthotrope, manuel de référence du logiciel de calcul de structure ICAB Force.
Tutoriel sur la déformation élastique d'une structure de poutres en nid d'abeille, Univ. Cambridge.

[Roffiaen-1] {a et b} Eug Roffiaen, Traité théorique et pratique sur la résistance des matériaux dans les constructions, Félix Oudart, 1858.

[2] Landau L.D. et Lipshitz E.M., Theory of Elasticity, 3^e éd., 1970, 1-172.

[3] L. R. G. Treloar, The Physics of Rubber Elasticity, Oxford, Clarendon Press, 1975, 310 p. (ISBN 978-0-19-851355-1), p. 2.

[a-4] {a et b} Gijsbertus de With, Structure, Deformation, and Integrity of Materials, volume I : Fundamentals and Elasticity, Weinheim, Wiley VCH, 2006, 838 p. (ISBN 978-3-527-31426-3), p. 32.

[5] La notion de module de compressibilité est ambiguë puisqu'il s'agit de l'inverse de ladite « compressibilité ».

[6] L'équation des gaz parfaits donne χ_T = 1/P, soit K = P = 10⁵ Pa = 10⁻⁴ GPa à 1 atm.

[1]

[2]

[3]

[4]

[5]

[6]