Problème de Monty Hall
| Type |
Problème mathématique (en), biais cognitif |
|---|---|
| Nommé en référence à |

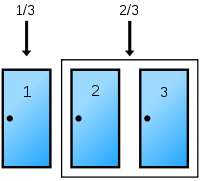
soient trois portes, cachant soit une chèvre soit une superbe voiture, l'automobile étant derrière une seule porte et les deux chèvres étant derrière les deux autres portes restantes.
Le problème de Monty Hall est une énigme mathématique[1], librement inspirée du jeu télévisé américain Let's Make a Deal. Il porte le nom de celui qui a présenté ce jeu aux États-Unis pendant treize ans, Monty Hall.
Simple dans son énoncé, mais non intuitif dans sa résolution, le problème de Monty Hall est parfois appelé « paradoxe de Monty Hall ».
Énoncé[modifier | modifier le code]
Le jeu oppose un présentateur à un candidat (le joueur).
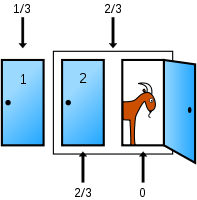
Le joueur est placé devant trois portes fermées. Derrière l'une d'entre elles, se trouve une voiture et derrière chacune des deux autres se trouve une chèvre. Le joueur doit tout d'abord désigner une porte. Puis le présentateur ouvre une porte qui n'est ni celle choisie par le candidat, ni celle cachant la voiture (le présentateur sait quelle est la bonne porte dès le début). Le candidat a alors le droit d'ouvrir la porte qu'il a choisie initialement, ou d'ouvrir la troisième porte. S'il ouvre la porte derrière laquelle se trouve la voiture, il l’emporte.
Les questions qui se posent au candidat sont :
- Que doit-il faire ?
- Quelles sont ses chances de gagner la voiture en agissant au mieux ?
Historique et évolution de l'énoncé du problème[modifier | modifier le code]
Ci-dessous est reproduite la traduction d'un énoncé célèbre du problème[2], issu d'une lettre que Craig F. Whitaker avait fait paraître dans la rubrique Ask Marilyn de Marilyn vos Savant du Parade Magazine en [3] :
« Supposez que vous êtes sur le plateau d'un jeu télévisé, face à trois portes et que vous devez choisir d'en ouvrir une seule, en sachant que derrière l'une d'elles se trouve une voiture et derrière les deux autres des chèvres. Vous choisissez une porte, disons la numéro 1, et le présentateur, qui sait, lui, ce qu'il y a derrière chaque porte, ouvre une autre porte, disons la numéro 3, qui découvre une chèvre. Il vous demande alors : « désirez-vous ouvrir la porte numéro 2 ? ». Avez-vous intérêt à changer votre choix ? »
La publication de cet article dans le Parade Magazine a eu un impact immédiat sur le lectorat et a engendré de très nombreuses discussions parmi les mathématiciens, célèbres ou non, et les amateurs anonymes. Marilyn vos Savant, réputée pour figurer au Guinness Book of Records comme étant la personne au quotient intellectuel le plus élevé au monde (QI de 228), a ainsi reçu plus de 10 000 lettres (estimation faite par elle-même) traitant du problème, dont plusieurs provenant d'universitaires remettant en question la pertinence de la démonstration reproduite dans sa rubrique. En 1991, pour une édition dominicale, la une du New York Times ouvre sur ce sujet. Jerry Pournelle, célèbre chroniqueur du Chaos Manor de Byte, a également discuté le problème longuement en tant qu'adversaire de la solution de Marilyn, pour se ranger en fin de compte à ses arguments. Enfin, une discussion controversée a eu lieu à propos de l'article du Parade Magazine dans la rubrique The Straight Dope tenue par Cecil Adams dans l'hebdomadaire The Chicago Reader.
La pertinence des résultats statistiques était parfois contestée : ce qui posait le plus souvent problème était que l'article n'insistait pas sur les « contraintes » du présentateur. Les résultats donnés impliquaient nécessairement les postulats suivants :
- Que le présentateur ne peut pas ouvrir la porte choisie par le candidat.
- Que le présentateur ouvre obligatoirement une porte dévoilant une chèvre et sans préférence s'il a le choix
- Que le présentateur donne systématiquement la possibilité au candidat de revenir sur son choix initial.
Or, comme ces éléments n'étaient pas mis en avant dans l'énoncé du problème, et ce même s'ils étaient implicites, d'autres résultats statistiques que ceux donnés dans l'article devenaient possibles.
En considérant que ces postulats étaient une condition sine qua non de l'énoncé du problème, il s'est avéré que les résultats de l'article étaient effectivement justifiés.
Finalement, cet énoncé s'inscrit dans la lignée de ceux consacrés à ce type de paradoxe. Une des premières apparitions de ce problème date de 1898 dans Probabilités de Calcul de Joseph Bertrand où il est décrit comme le paradoxe des boîtes de Bertrand (à ne pas confondre avec le paradoxe de Bertrand).
Un énoncé exempt d'ambiguïté[modifier | modifier le code]
Il est préférable de se fonder sur un énoncé non équivoque du problème, incluant les contraintes du présentateur, décrit par Mueser et Granberg comme suit :
- Soient trois portes, l'une cache une voiture, les deux autres une chèvre. Les prix sont répartis par tirage au sort.
- Le présentateur connaît la répartition des prix.
- Le joueur choisit une des portes, mais rien n'est révélé.
- Le présentateur ouvre une autre porte ne révélant pas la voiture.
- Si le joueur choisit une porte à chèvre, le présentateur ouvrira la seule autre porte à chèvre.
- Si le joueur choisit la porte à voiture, le présentateur ouvrira au hasard une des deux portes à chèvre (éventuellement préalablement désignée par tirage au sort).
- Le présentateur propose au candidat de changer son choix de porte à ouvrir définitivement.
La question qui se pose alors est :
- Le joueur augmente-t-il ses chances de gagner la voiture en changeant son choix initial ? C'est-à-dire : la probabilité de gagner en changeant de porte est plus grande que la probabilité de gagner sans changer de porte ?
Une solution rapide et non-ambiguë[modifier | modifier le code]
La solution la plus simple repose sur les dénombrements, soit le comptage du nombre de cas satisfaisants, insatisfaisants et total. Voici sa formulation : « Après ouverture de la porte, il y a deux cas sur trois où le prix se cache derrière l'autre porte ».
Explications :
- Les « trois cas » font référence aux trois cas du jeu : {choix d'une chèvre, choix d'une chèvre, choix du prix}.
- Les « deux cas » font référence aux deux cas désavantageux : {choix d'une chèvre, choix d'une chèvre}.
- Comme une probabilité s'exprime en tant que quotient des nombres de cas, et comme la porte ne s'ouvre jamais sur le prix, on a donc deux chances sur trois d'être face aux choix « garder une chèvre ou la changer pour le prix ».
Développement[modifier | modifier le code]
On numérote les cas et on définit les événements en fonction du choix initial comme suit :
- cas 1 (C1) : le candidat a choisi la porte de la chèvre 1
- cas 2 (C2) : le candidat a choisi la porte de la chèvre 2
- cas 3 (V) : le candidat a choisi la porte de la voiture
Ces trois événements sont équiprobables :
On observe maintenant le déroulement de la suite dans chacun de ces trois cas :
- cas 1 : Le candidat ayant initialement choisi la porte de la chèvre 1, le présentateur ouvre la porte de la chèvre 2. La porte restante cache la voiture.
- cas 2 : Le candidat ayant initialement choisi la porte de la chèvre 2, le présentateur ouvre la porte de la chèvre 1. La porte restante cache la voiture.
- cas 3 : Le candidat ayant initialement choisi la porte de la voiture, le présentateur ouvre la porte d'une des deux chèvres. La porte restante cache une chèvre.
On voit ici aisément que dans 2 cas sur 3, la porte restante cache la voiture.
Traduction en probabilités[modifier | modifier le code]
On ajoute donc aux événements précédents les trois événements suivants :
- C : le candidat a choisi initialement une des deux portes à chèvre. On a alors
- GVC : le candidat Gagne la Voiture en Changeant de porte
- GVS : Le candidat Gagne la Voiture Sans changer de porte
- Le joueur change de porte
On a vu précédemment que lorsque le candidat avait choisi initialement une porte à chèvre, changer de porte le menait forcément à gagner la voiture, soit :
On a aussi vu qu'en ayant initialement choisi la voiture, changer de porte menait forcément le candidat à ouvrir une porte à chèvre. Donc :
La probabilité de gagner en changeant de porte s'écrit donc comme suit :
- Le joueur ne change pas de porte
Dans ce cas, le candidat ne gagne que s'il avait choisi initialement la voiture, on a donc :
La probabilité de gagner sans changer de porte s'écrit donc comme suit:
Controverse[modifier | modifier le code]
Si l'on demande une réponse rapide et intuitive, deux points de vue incompatibles s'opposent.
- Le premier affirme qu'après ouverture de la porte, il reste deux portes, chacune ayant tout autant de chances de cacher la voiture. On a donc tout autant de chances de gagner avec changement que sans changement (ce point de vue consiste en fait à ignorer comment la porte ouverte dévoilant la chèvre a été sélectionnée).
- Le second affirme que si l'on ne change pas de porte, on gagne si et seulement si on avait fait le bon choix au départ. Or, ce choix avait une chance sur trois d'être bon. Il y a donc de chances de gagner sans changer, de chances de gagner en changeant.
Ce problème a longtemps été un cas de paradoxe probabiliste (à l'instar du problème de la Belle au bois dormant) pour lequel il existe deux solutions contradictoires défendables sans qu'on parvienne à faire triompher une interprétation. La solution et s'impose, en particulier après la réalisation de simulations d'un grand nombre de tirages — c'est en particulier seulement ainsi que le mathématicien Paul Erdős admit cette solution [réf. souhaitée] ; la simulation est ici si simple à programmer que ses résultats sont indiscutables. Le premier point de vue est une illusion de parité due au fait qu'un choix est demandé sur les deux portes restantes. Mais les espérances de gain associées à ces portes ne sont pas identiques.
En supposant que le participant pense que le présentateur ouvre une des deux portes restantes au hasard, le résultat serait différent : on constitue la liste les triplets de choix de la forme (1er choix participant, choix présentateur, porte restante) dont les éléments sont notés C pour chèvre, V pour voiture : (C,C,V), (C,V,C), (C,C,V), (C,V,C),(V,C,C), (V,C,C). Après dévoilement de la première porte qui est C, les cas (C,V,C) sont donc exclus, et le participant conclut avoir les cas suivants de façon équiprobable (il le sont) : (C,C,V), (C,C,V), (V,C,C), (V,C,C). À ce moment il voit deux cas sur quatre où l'autre porte est V et deux autres cas où elle est C, soit une chance sur deux de gagner ou perdre en gardant son choix.
Les hypothèses importantes[modifier | modifier le code]
- Les trois portes ont, tant qu'aucune n'est ouverte, la même probabilité d'être la porte gagnante : 1⁄3. pour chacune.
- Le présentateur doit ouvrir une porte, et celle-ci ne peut être ni la porte choisie par le joueur, ni la porte gagnante. Ces conditions sont toujours disponibles et il peut y répondre sans risque d'erreur puisqu'il connaît les emplacements.
- Quand le présentateur a le choix entre deux portes à ouvrir (elles sont alors toutes deux perdantes), il choisit arbitrairement entre les deux, avec équiprobabilité.
Ces hypothèses sont toutes importantes et on verra que la modification de n'importe laquelle conduit à un résultat différent. Mais souvent, l'usage de plusieurs de ces hypothèses est implicite.
Réfutation des arguments pro-1/2[modifier | modifier le code]
Longtemps le raisonnement développé ci-dessus n'a pas fait l'unanimité. Il lui était reproché de considérer que l'ouverture d'une mauvaise porte laisse inchangée la probabilité pour que la porte initialement choisie soit la bonne : 1⁄3. Il est effectivement légitime de se demander pourquoi l'ouverture de la troisième porte ne modifie la probabilité que de l'une des deux portes : c'est la notion de probabilité conditionnelle, et, en fait, toute probabilité, explique Myron Tribus, est conditionnelle à un état de connaissance.
Ceux qui refusent ce raisonnement (les personnes pro-1⁄2) considèrent que la situation après ouverture d'une porte est équivalente à ouvrir une mauvaise porte avant le choix du candidat. Ils affirment par conséquent que la probabilité de gagner est la même en changeant ou sans changer, soit 1⁄2.
L'erreur de ce type de raisonnement est de ne retenir que l'événement « une porte a été ouverte ». Si une porte était ouverte strictement au hasard parmi les deux portes non choisies, et qu'elle révélait une chèvre, la probabilité deviendrait effectivement 1⁄2 pour chacune des deux autres portes, parce qu'exclure les cas où le présentateur ouvrirait la porte cachant la voiture améliore de fait la probabilité que la voiture soit derrière la porte choisie initialement.
En revanche, après ouverture de la porte par l'animateur, la probabilité que la voiture soit derrière la porte non ouverte et non choisie par le joueur a progressé : dans le cas où la voiture est derrière une des deux portes non choisies par le joueur (2 chances sur 3), l'animateur a éliminé la chèvre (le mauvais choix pour le joueur), il ne reste donc que la voiture.
En changeant son choix le joueur a donc une probabilité de 2⁄3 × 1 = 2⁄3 de trouver la voiture.
Pour une démonstration formelle, voir le paragraphe « résolution par la formule de Bayes ».
Raccordement des différents calculs[modifier | modifier le code]
Pour faire le calcul avant ouverture de la porte, il faut raisonner ainsi : on doit envisager la possibilité que la porte choisie initialement soit la bonne, et celle que chacune des deux autres portes soit la bonne. Il faut alors penser à l'issue de chacune de ces possibilités, c'est-à-dire se demander quelle porte sera ouverte par le présentateur (4 sous-cas en tout) et ce qu'il faudra faire alors pour gagner. On voit rapidement que la probabilité de gagner en changeant est égale à 1-p, p étant la probabilité pour la porte initialement choisie d'être la bonne, ici 1⁄3 (Hypothèse 1a). Donc ici, on gagne 2 fois sur 3 en changeant. Il est important ici de se rappeler qu'il n'y a jamais de remise (Hypothèse 2), sans quoi le raisonnement précédent n'est plus valable.
La probabilité est-elle inchangée par l'ouverture (plus précisément : par le choix fait par le présentateur entre les deux portes dont on envisageait l'ouverture) ? Pas forcément, mais tels que les calculs ont été faits, les situations après ouverture sont des sous-cas du calcul précédent. Donc, sans affirmer immédiatement que la probabilité est inchangée, la moyenne pondérée des probabilités correspondant à chaque porte ouverte par le présentateur doit correspondre au calcul précédent. Prétendre qu'on a 1 chance sur 2 de gagner sans changer quelle que soit la porte ouverte est donc incohérent.
Pour évaluer les chances après ouverture, il suffit en fait de constater qu'il y a après choix totale symétrie entre les 2 portes non choisies (Hypothèses 1b et 3). Puisque la moyenne pondérée doit valoir 2⁄3 et que les sous-cas doivent donner le même résultat, on retrouve bien 2 chances sur 3 de gagner en changeant quelle que soit la porte ouverte. Il était donc important de préciser que quand deux portes peuvent être ouvertes, le choix est équiprobable.
Le résultat 2⁄3 est donc parfaitement valide, mais il convient de ne pas l'annoncer sans préciser qu'il repose sur la parfaite symétrie des rôles des portes non choisies. En brisant cette symétrie, tous les résultats sont possibles.
De plus, le raisonnement a employé le fait que le jeu n'autorise jamais la remise. Si le présentateur n'agit pas en exploitant sa connaissance de la véritable porte, les précédents calculs ne s'appliquent pas.
Clés pour comprendre le problème[modifier | modifier le code]
Raisonnement par la probabilité que le présentateur apporte de l'information[modifier | modifier le code]
Prenons le cas d’un candidat qui suit toujours la même stratégie à chaque jeu, celle de maintenir systématiquement son premier choix. Ce candidat aura donc 1 chance sur 3 de gagner la voiture. En moyenne, il gagnera donc une fois sur trois et perdra forcément 2 fois sur 3, exactement comme si le présentateur n'ouvrait pas de porte.
Au contraire, un candidat qui suit la stratégie inverse, changer systématiquement son premier choix, gagnera en moyenne 2 fois sur 3, en effet, lorsque le présentateur ouvre une porte deux cas de figure sont possibles :
- soit le candidat avait choisi la voiture (1 chance sur 3) et le présentateur ouvre n'importe quelle porte, n'apportant pas d'information,
- soit le candidat avait choisi une chèvre (2 chances sur 3) et le présentateur ouvre la porte de la seule chèvre restante, désignant de fait la porte restante comme celle cachant la voiture.
Donc faire confiance au présentateur en changeant son choix apporte 2 chances sur 3 de gagner.
On note au passage que le présentateur n'a absolument aucune liberté dans le fait d'apporter de l'information ou non, donc que sa volonté d'aider ou de nuire n'a aucun effet.
Raisonnement par les probabilités complémentaires[modifier | modifier le code]
Lorsque le candidat choisit une porte, il y a 1 chance sur 3 que ce soit celle de la voiture, et 2 chances sur 3 qu'il y ait une chèvre derrière. Ces probabilités sont des probabilités a priori et ne changeront donc jamais pendant toute la durée du jeu. Lorsque le présentateur fait sortir une chèvre, la probabilité d'avoir la voiture derrière la porte choisie est toujours de 1/3, et donc la probabilité que la voiture soit derrière la porte restante est de 2/3. D'où l'intérêt pour le candidat de choisir la porte restante et de changer son choix.
Diagrammes[modifier | modifier le code]
La probabilité que la voiture se trouve derrière la porte restante peut être calculée avec les diagrammes ci-dessous.
Après avoir choisi la porte numéro 1, par exemple, le candidat a une chance sur trois de tomber directement sur la voiture et deux chances sur trois que la voiture soit parmi les deux portes restantes.
Puisqu'il n'y a qu'une seule voiture, il y a 100 % de chance qu'il y ait une chèvre derrière au moins une des portes 2 ou 3.
Le présentateur ouvre maintenant la porte 3. Bien sûr, le présentateur n'ouvre jamais une porte donnant sur la voiture, donc sans surprise la porte 3 donne sur une chèvre ce qui a pour effet de transférer la probabilité de 2⁄3 de chances d'avoir une voiture non plus sur les portes 2 et 3 comme expliqué précédemment, mais uniquement sur la porte 2 (voir graphique ci-dessous).
-
Probabilités des deux groupes de portes : celle sélectionnée (1) et les deux non sélectionnées.
-
Après ouverture, les probabilités pour les deux groupes restent les mêmes mais la probabilité de la porte ouverte (3) devient 0 et celle de sa voisine (2) devient 2/3.
De manière encore plus simple, on peut reformuler en disant que si après le choix initial du candidat il était envisageable que la voiture se trouve derrière les portes 2 et 3 (avec une probabilité de 2⁄3), ce n'est plus le cas après l'ouverture de la porte 3 par le présentateur : seule la porte 2 est encore susceptible de cacher la voiture (et par conséquent, toujours avec une probabilité de 2⁄3).
Le diagramme ci-dessous montre le même raisonnement d'une manière plus complète et plus formalisée :
Reformulons l'énoncé pour rendre le résultat intuitif[modifier | modifier le code]
La description du problème induit en erreur en amenant à comparer les probabilités sur deux portes (la première sélectionnée et celle qui reste après l'intervention du présentateur) qui semblent intuitivement identiques depuis le début du jeu. En réalité, la porte ouverte par le présentateur dépend de la première sélectionnée et n'est donc pas neutre pour la suite. La façon de présenter le jeu ci-dessous est tout à fait équivalente, mais les raisons de la répartition finale 1⁄3-2⁄3 apparaissent beaucoup plus intuitives, car on évite cette comparaison.
Gardons les mêmes règles du jeu :
- Première étape : le joueur élimine arbitrairement une des trois portes : il y a deux chances sur trois que la voiture soit derrière l'une ou l'autre des deux restantes.
- Deuxième étape : Le présentateur regarde derrière les portes restantes et en ouvre une avec la contrainte qu'elle cache une chèvre.
- Comme la voiture n'est pas derrière la porte ouverte par le présentateur, la probabilité que la voiture soit derrière la dernière porte est de 2⁄3... Et la probabilité qu'elle soit derrière la porte qui a été exclue à la première étape est donc -toujours- de 1⁄3.
En d'autres termes, si la porte exclue à la première étape cache une chèvre (il y a 2 chances sur 3), l'intervention de l'animateur consiste exactement à indiquer avec certitude que la voiture.se trouve derrière la troisième porte. Inversement, si la porte exclue à la première étape cache la voiture (1 chance sur 3), la troisième cache une chèvre.
On peut noter que le présentateur n'a pas besoin de connaître ce qui est derrière la porte désignée à la première étape.
Simulation[modifier | modifier le code]
Comme démontré précédemment, les valeurs théoriques données par les lois des probabilités sont donc :
- 1⁄3 de chances de gagner la voiture sans changer son choix initial, soit environ 33,3 % ;
- 2⁄3 de chances de gagner la voiture en changeant son choix initial, soit environ 66,7 %.
Mais on peut également pratiquer une simulation à l'aide d'un programme informatique reproduisant des parties fictives et voir si, sur un grand nombre de parties, le résultat simulé tend vers le résultat donné par les probabilités et les confirment. Pour cela deux cas sont à distinguer :
- le cas où il y a un changement du choix initial ;
- le cas où le choix initial est conservé.
Dans chaque cas, il convient de réaliser un grand nombre de situations pour réduire la marge d'erreur et de noter le pourcentage où le candidat gagne la voiture.
Plusieurs simulations, dont certaines sur Internet (Laboratoire de Mathématiques Raphaël Salem, pour versions Internet explorer 4 ou +, en anglais) confirment les résultats théoriques d'1⁄3 et de 2⁄3 et ce d'autant plus que le nombre d'itérations est important ; on peut calculer la probabilité d'avoir de tels résultats en supposant que la vraie probabilité serait 1⁄2-1⁄2, elle peut être rendue arbitrairement petite en augmentant le nombre d'essais (on n'a pas signalé de simulation apportant un résultat contraire ; la confirmation du résultat 1⁄3-2⁄3 ne repose pas que sur les expériences, mais sur leur reproductibilité).
C'est cet argument qui vient à bout d'un scepticisme bien naturel, et qui a fini par convaincre Paul Erdös au départ très réticent lui-même[4], si l'on en croit Le Figaro Magazine[réf. souhaitée]. Il est en général plus facile de se tromper dans une simulation que dans un raisonnement, même probabiliste, mais celle-ci est tellement simple à écrire qu'elle ne laisse guère de place à l'erreur, quoi qu'en suggère son résultat fortement contre-intuitif.

Problème cousin : les trois prisonniers[modifier | modifier le code]
Bien que ce problème soit isomorphe à celui de Monty Hall, son interprétation ne déclenche curieusement pas de déni comparable :
Alors que trois prisonniers risquent l'exécution, l'un d'eux apprend de source sûre que l'un des trois a été gracié en dernière minute. Le gardien refuse de lui donner le nom du gracié, mais accepte de lui donner le nom de l'un des condamnés, qui n'est pas le sien. Le prisonnier doit-il se montrer rassuré en entendant le nom d'un des deux autres ?
On peut le croire, et penser que les chances de survie du prisonnier sont passées de 1⁄3 à 1⁄2. En réalité, ce problème est exactement le même que celui de Monty Hall et on démontre de la même façon que les chances pour le prisonnier d'être gracié sont toujours de 1⁄3. Par contre, le troisième prisonnier, celui qui n'a pas été désigné, a maintenant deux chances sur trois de s'en sortir.
Résolution par la formule des probabilités totales[modifier | modifier le code]
En notant l'événement « Le joueur gagne la voiture » et celui « Le joueur avait choisi la bonne porte » on a, par la formule de probabilités totales :
- Dans la stratégie où le joueur ne change pas de porte, il gagne si et seulement s'il avait choisi initialement la bonne porte : et . Ainsi, .
- Dans la stratégie où le joueur change de porte, il gagne si et seulement s'il avait choisi initialement la mauvaise porte : et . Ainsi, .
Résolution par le théorème de Bayes[modifier | modifier le code]
L'énoncé renvoie en définitive à un problème de probabilité conditionnelle et selon la formulation générale du théorème de Bayes :
- Soit un événement quelconque, de probabilité non nulle.
- Soit un ensemble d'événements, chacun de probabilité non nulle, à la fois exhaustifs et mutuellement exclusifs.
Alors pour tout , on a :
Une application du théorème de Bayes au problème de Monty Hall pourrait être formulée ainsi :
Considérons le cas où la porte 3 a été choisie et aucune porte n'est encore ouverte. La probabilité que la voiture soit derrière la porte 2, , est de 1⁄3, probabilité qui serait en outre exactement la même pour chaque porte.
La probabilité que le présentateur ouvre la porte 1, , est alors de 1⁄2. En effet, le candidat ayant choisi la porte 3 et le présentateur sachant ce que cache chaque porte :
- Soit la voiture est derrière la porte 1 : le présentateur ouvrira la porte 2.
- Soit la voiture est derrière la porte 2 : le présentateur ouvrira la porte 1.
- Soit la voiture est derrière la porte 3 : le présentateur ouvrira la porte 1 ou le présentateur ouvrira la porte 2 (équiprobabilité 1⁄2).
La probabilité que le présentateur ouvre la porte 1 sachant que la voiture est derrière la porte 2 est donc . La probabilité que la voiture soit derrière la porte 2 sachant que le présentateur ouvre la porte 1 est donc (par le théorème de Bayes) :
Variantes[modifier | modifier le code]
De nombreuses variantes ont été proposées, modifiant les paramètres. Il est souvent possible de trouver la solution de chaque problème par un raisonnement simple, comme dans le problème principal, mais la difficulté à saisir le rôle de chaque hypothèse conduit souvent à une réponse erronée, et il est donc préférable de résoudre le problème analytiquement.
Cas d'un nombre élevé de portes[modifier | modifier le code]
Il est peut-être plus facile d'appréhender le résultat décrit ci-dessus en considérant 100 portes et non plus trois comme précédemment. Lorsque le candidat choisit une porte, la probabilité qu'il tombe directement sur la porte cachant le prix de valeur est très faible (1 %).Le présentateur ouvre 98 portes d'un coup, révélant obligatoirement 98 chèvres, tout en proposant toujours ensuite au candidat de changer son choix initial et de choisir l'autre porte non ouverte. Il y a 99% de chances que le prix se trouve dans les 99 portes restantes. Comme 98 ont été ouvertes, à 99 % la dernière porte contient à coup sûr le prix de valeur. Le candidat aura donc tout intérêt à changer son choix initial.
La démonstration est la même, mais le résultat est plus intuitif : il paraît tellement suspect que toutes les portes non choisies aient été ouvertes sauf une.
On pourrait aussi laisser plus d'une des portes non choisies fermées, et même autoriser à sélectionner plus d'une porte au départ (le présentateur ne pourra ouvrir aucune des portes sélectionnées). Généralement, partant de n portes fermées, après que le candidat a désigné c porte(s), le présentateur ouvre m porte(s), m étant un entier entre 0 et n-c-1. Les chances d'être la bonne porte sont de :
- 1⁄n pour une des c porte(s) choisie(s) initialement
- pour chacune des autres portes.
Il est équivalent d'ouvrir m portes une par une si le candidat refuse entre chaque ouverture de changer un de ses choix ou d'ouvrir les m portes en même temps.
Ces formules s'obtiennent par calcul avec un arbre, mais on peut les trouver immédiatement en utilisant le fait que quand les portes ont à l'origine toutes la même probabilité de cacher la voiture, l'ouverture laisse les probabilités inchangées pour les portes choisies à l'origine.
Soudoyons les organisateurs[modifier | modifier le code]
Jusqu'ici, nous avons toujours supposé que les portes avaient à l'origine une probabilité égale de cacher la voiture. Que se passe-t-il si ce n'est plus le cas ?
On peut par exemple imaginer que le candidat a dragué l'assistant du présentateur, qui lui a révélé que la porte de droite cache une chèvre. Mal avisé, le candidat choisit d'abord la porte du milieu. Le présentateur ouvre alors la porte de gauche. Quelles sont les probabilités ?
- Si on a pleinement confiance dans l'assistant, 1 pour la porte centrale, 0 pour la porte de droite
- Si l'assistant ignorait tout et prétendait savoir pour se rendre intéressant, le problème est équivalent au problème initial, 1⁄3 pour la porte centrale, 2⁄3 pour la porte de droite
- Si l'assistant a cherché à induire le candidat en erreur, 0 pour la porte centrale, 1 pour la porte de droite
On trouve une formule générale en appliquant le théorème de Bayes : on numérote arbitrairement 1 la porte choisie à l'origine, 2 la porte ouverte par le présentateur et 3 la dernière porte ; on note la probabilité à l'origine pour que la porte i cache la voiture.
les chances sont après ouverture de pour la porte 3 (avec changement) et de pour la porte 1 (sans changement).
En fait, il est correct de dire que la porte choisie initialement a sa probabilité de cacher la voiture inchangée si elle est nulle ou bien si , ou plus généralement pour n portes si la probabilité moyenne des portes ouvertes pour cacher la voiture était égale à la probabilité moyenne des portes non choisies pour cacher la voiture.
Rappelons qu'il est équivalent de dire que la porte choisie initialement a sa probabilité de cacher la voiture inchangée ou que les portes non choisies non ouvertes ont hérité de la probabilité des portes ouvertes.
On trouvera une analyse beaucoup plus détaillée de situations analogues, où on ne s'occupe plus directement de probabilités, mais de stratégies (au sens de la théorie des jeux) dans un article récent de Sasha Gnedin (en)[5].
Changeons les règles d'ouverture[modifier | modifier le code]
On doit à Jean-Paul Delahaye deux variantes qui éclairent bien sur l'importance des règles de l'ouverture de la porte. Dans un article de Pour la Science[6], il proposait que le présentateur ouvre une porte prise au hasard parmi les deux portes non sélectionnées par le candidat (il peut éventuellement avoir décidé si la porte serait la plus à gauche ou à droite avant que le candidat ne désigne une porte), le jeu recommençant à zéro s'il ouvrait la porte cachant une voiture. Une seconde variante propose d'ouvrir une porte prise au hasard parmi les deux portes cachant une chèvre, le jeu recommençant s'il ouvrait la porte sélectionnée par le candidat.
Delahaye affirma que les résultats de ces variantes étaient équivalents à ceux du problème original. Mais le courrier des lecteurs lui fit se reprendre : les probabilités sont de 1⁄3 pour que le changement soit gagnant, 1⁄3 pour que le maintien du choix initial soit gagnant, 1⁄3 pour qu'il y ait remise… Soit sur l'ensemble du jeu (après autant de remises qu'il aura fallu) 1 chance sur 2 de gagner quelle que soit la stratégie adoptée lors de la première manche non annulée.
On saisit ici l'importance des règles du jeu qui conditionnent l'ouverture d'une porte à la fois au choix du joueur et à la position de la bonne porte.
Introduisons encore quelques variantes pour mieux comprendre :
La porte ouverte par le présentateur est choisie parmi les 3 portes sans tenir compte ni du choix ni de la place de la voiture : on trouve cette fois 5 chances sur 9 de remise, 2 chances sur 9 de gagner en changeant, 2 chances sur 9 de gagner sans changer. Là encore, probabilité égale de gagner ultimement avec ou sans changement.
Le présentateur ouvre une des deux portes non choisies par le candidat, en choisissant 3 fois sur 4 la porte cachant la voiture si elle en fait partie : cette fois il y a une chance sur 2 de remise, 1 sur 3 de gagner sans changer et 1 sur 6 de gagner en changeant ! Ultimement, 2 chances sur 3 de gagner sans changer. En biaisant les règles, on peut inverser l'efficacité des stratégies.
Plus généralement, s'il y a une probabilité p pour que la porte cachant la voiture soit ouverte (annulant la manche) quand elle n'a pas été sélectionnée, on 1⁄3 chance de gagner sans changer, 2×(1-p)⁄3 chance de gagner en changeant, 2p⁄3 chance de remettre en jeu. Ultimement, il y a 1⁄(3-2p) chance de gagner sans changer, 1-1⁄(3-2p) en changeant.
Dernière variante : le présentateur ouvre une porte ne cachant pas la voiture et non choisie par le candidat, mais pas au hasard : au contraire, le joueur sait qu'il ouvre systématiquement la plus à droite des portes répondant aux précédents critères.
- si le présentateur ouvre la porte restante la plus à gauche : il est certain que la voiture est derrière la porte restante de droite
- si le présentateur ouvre la porte restante la plus à droite ; il exclut 2 cas sur les 6 initiaux et les deux portes restantes deviennent équiprobables
Donc, la probabilité de gagner en changeant n'est plus de 2⁄3 mais de 1 ou de 1⁄2 selon les cas, l'espérance totale restant de 2⁄3.
Généralisons encore : si la porte qui a été ouverte avait une probabilité p d'être ouverte s'il y avait le choix, la probabilité de gagner est de 1⁄(1+p) en changeant et de p⁄(1+p) sans changer. Avantage toujours au changement.
Cas du jeu À prendre ou à laisser[modifier | modifier le code]
Des parallèles ont souvent été évoqués entre le problème de Monty Hall et le jeu Deal or No Deal, adapté sous le nom d’À prendre ou à laisser en France. En effet, le jeu comporte un certain nombre de boîtes contenant une variété de sommes allant du très faible au très élevé, qu'il faut éliminer jusqu'à n'en avoir plus que deux. Il est donc simple de comparer les deux expériences pouvant se ramener au même principe d'ouverture de portes.
Cependant, il existe une différence majeure qui fait que le problème de Monty Hall ne s'applique pas dans À prendre ou à laisser. En effet, dans ce dernier, ce n'est pas le présentateur qui ouvre une porte, qui cache obligatoirement un prix de faible valeur (sachant ce qu'il y a derrière les portes), mais le candidat lui-même, qui n'a aucune information. Ainsi, lorsqu'il décide d'ouvrir une boîte, la probabilité d'éliminer un prix de forte valeur n'est pas nulle, là où dans le cas de Monty Hall, cette probabilité est nulle.
De ce fait, lorsque le choix est proposé au candidat d'échanger sa boîte avec la dernière restante (dans le cas où il reste un prix de faible valeur et un autre de forte valeur), étant donné qu'il a éliminé toutes les autres boîtes de manière aléatoire, la probabilité de gagner le gros lot en échangeant sa boîte reste de 1⁄2.
Exemple concret avec 3 boîtes restantes, A et B contenant 1 € et C contenant 1 000 000 €. Chaque événement est équiprobable.
- Le candidat a la boîte A, il élimine la boîte B, il n'échange pas : perdu.
- Le candidat a la boîte A, il élimine la boîte B, il échange : gagné.
- Le candidat a la boîte A, il élimine la boîte C : perdu avec ou sans échange.
- Le candidat a la boîte B, il élimine la boîte A, il n'échange pas : perdu.
- Le candidat a la boîte B, il élimine la boîte A, il échange : gagné.
- Le candidat a la boîte B, il élimine la boîte C : perdu avec ou sans échange.
- Le candidat a la boîte C, il élimine la boîte A, il n'échange pas : gagné.
- Le candidat a la boîte C, il élimine la boîte A, il échange : perdu.
- Le candidat a la boîte C, il élimine la boîte B, il n'échange pas : gagné.
- Le candidat a la boîte C, il élimine la boîte B, il échange : perdu.
Lorsqu'il ne reste plus que 3 boîtes, il a donc une probabilité de 4⁄12 (= 1⁄3) de remporter le gros lot. Cependant, il a aussi une probabilité de 1⁄3 d'éliminer cette boîte contenant le gros lot. Par conséquent, dans les 8 cas possibles où il n'a pas éliminé le gros lot, il y a autant de chances de gagner en échangeant qu'en gardant sa boîte : 1⁄2.
Il faut cependant noter que dans À prendre ou à laisser, il y a deux subtilités à connaître : le banquier, qui peut proposer un échange, peut également proposer une somme d'argent. La deuxième subtilité est que le banquier connaît le contenu des boîtes : ainsi, en fonction de ce qu'il propose, il peut influer sur la décision du candidat et tourner la situation à son propre avantage.
Formule globale[modifier | modifier le code]
Donnons une formule globale pour toutes les variantes des deux paragraphes précédents. On notera :
- concernant les probabilités avant ouverture (ces probabilités peuvent traduire par exemple le fait que le candidat est presque sûr d'avoir entendu une chèvre derrière une porte) :
- la probabilité pour la porte initialement choisie soit la bonne
- la probabilité pour la porte qui est ensuite ouverte soit la bonne
- la probabilité pour la troisième porte soit la bonne
Et on a (et même dans le problème traditionnel)
- quand la porte choisie initialement est mauvaise :
- la probabilité pour que le présentateur choisisse d'ouvrir la porte initialement choisie par le candidat (annule la manche, dans le problème traditionnel)
- la probabilité pour que le présentateur choisisse d'ouvrir la porte cachant la voiture (annule la manche, dans le problème traditionnel)
- la probabilité pour que le présentateur ouvre la troisième porte ( dans le problème traditionnel)
Et on a
- quand la porte choisie initialement est la bonne
- la probabilité pour que le présentateur ouvre la porte « interdite », choisie et cachant la voiture (annule la manche, dans le problème traditionnel)
- la probabilité qu'avait d'être ouverte la porte qu'il a justement ouverte quand il peut choisir (représente par exemple la préférence du présentateur pour la gauche, dans le problème traditionnel)
- la probabilité qu'avait d'être ouverte l'autre porte (même remarque que précédemment, dans le problème traditionnel)
Et on a
Les probabilités sont :
- P(remise)=
- P(le jeu se termine à cette manche)=
- P(gain en changeant) =
- P(gain en maintenant le choix initial) =
pour une manche
Et ultimement (en ayant remis en jeu autant de fois que nécessaire) :
- P(gain en changeant) =
- P(gain en maintenant le choix initial) =
Les probabilités de gain final pour chacune des stratégies est égale à la probabilité de gain sur une manche sachant que cette manche aboutira.
Ces formules s'obtiennent sans trop de difficultés par calcul avec un arbre.
Problème quantique[modifier | modifier le code]
Une variante audacieuse consiste à transposer le problème dans le monde de la physique quantique. Il ne s'agit plus d'ouvrir des portes mais de réaliser des mesures sur un système. Cette fois comme on choisit un vecteur de mesure, les possibilités sont illimitées.
Les situations qui en résultent sont variables. Selon qu'on autorise le joueur seulement, le présentateur seulement ou les deux à utiliser à leur avantage les phénomènes, les probabilités sont plus ou moins en faveur du joueur, mais de façon un peu analogue au problème traditionnel, la mauvaise stratégie est de conserver son vecteur initial et la bonne est de choisir un vecteur orthogonal au vecteur initial[7].
Dans la culture[modifier | modifier le code]
Littérature[modifier | modifier le code]
Roman[modifier | modifier le code]
L'écrivain et scénariste britannique Mark Haddon expose et démontre le Problème de Monty Hall dans son roman le Bizarre Incident du chien pendant la nuit, ainsi que Bernard Werber à plusieurs reprises. Dans le roman PopCo de Scarlett Thomas, Alice explique le raisonnement lié au problème de Monty Hall, et la controverse qu'il engendre par ses détracteurs. Robert J. Sawyer l'évoque dans son roman Veille. Dans son roman Sweeth Tooth de Ian McEwan, l'héroïne Serena Frome explique le problème de Monty Hall à son amant et auteur Tom Haley, qui en tirera une nouvelle[8].
Filmographie[modifier | modifier le code]
Cinéma[modifier | modifier le code]
Dans le film Las Vegas 21, un film de blackjack, un professeur du MIT de Boston demande à son étudiant de résoudre le problème de Monty Hall pour voir s'il est assez bon pour rejoindre son club de blackjack. L'élève répond qu'il y a deux fois plus de chances avec un changement, ce qui est une bonne réponse.
Télévision[modifier | modifier le code]
On retrouve également ce problème dans l'épisode 13 de la première saison de la série Numb3rs, quand le professeur de mathématiques Charlie Eppes (interprété par David Krumholtz) tente de l'enseigner à ses élèves.
L'épisode 12 Le problème de Monty Hall ou les probabilités changent de porte de Voyages au pays des maths aborde cette question.
Dans l'épisode 8 de la série Sūgaku Joshi Gakuen (数学♥女子学園) Nina (interprété par Tanaka Reina) est confrontée au problème de Monty Hall lors de son défi contre Satoko (interprété par Nakajima Saki).
Dans l'épisode 8 de la saison 4 de la série Brooklyn Nine-Nine, le capitaine Holt et Kevin se disputent pour savoir qui a raison quant à la résolution de ce problème (c'est Amy Santiago qui confirme la réponse des 2/3 à Holt).
Dans l'épisode 11 de la saison 41 de Survivor, le présentateur Jeff Probst met en place le même problème pour l'un des candidats de la saison : Deshawn pour sa "survie" dans le jeu.
Dans l’épisode 4 «That Monty Hall Problem » de la saison 1 de D.P., le déserteur, passionné de probabilités, pose un problème de Monty Hall aux enquêteurs.
Jeu vidéo[modifier | modifier le code]
Dans le jeu vidéo Zero Time Dilemma, l'équipe C composée de Carlos, Junpei et Akane est confrontée au problème de Monty Hall. Ils sont tous les trois enfermés dans une salle hermétique ne s'ouvrant qu'après un delai de 20 minutes et Zéro, le maître du jeu, inonde l'air d'un gaz irrespirable. L'équipe C est alors confrontée à une mort certaine mais se trouve face à un ensemble de 10 casiers, dont l'un contient un masque à gaz; ils n'ont le droit qu'à un seul choix. Le joueur incarnant Carlos cette fois-ci doit choisir un casier. Zéro leur communique la suite des règles: il va ouvrir 8 casiers vides sauf celui contenant le masque et celui choisi par Carlos/le joueur et celui-ci aura le choix de conserver son choix ou changer avec le casier restant. Junpei, d'abord abattu, saute de joie à l'idée que leur chance de trouver le masque soit réduite à un choix à 50-50, alors qu'il s'agit d'un choix à 10-90.
Culture populaire[modifier | modifier le code]
Le problème de Monty Hall est aujourd'hui entré dans la culture populaire, en particulier sur internet et dans les cercles universitaires, où il apparaît dans de nombreux Mèmes. Il apparait notamment dans une page du webcomic Xkcd[9].
Notes et références[modifier | modifier le code]
- (en) « Fallacies, Flaws, and Flimflam. The problem of cars and goats », The College Mathematics Journal, vol. 24, no 2, , p. 149–154 (ISSN 0746-8342 et 1931-1346, DOI 10.1080/07468342.1993.11973519, lire en ligne, consulté le )
- (en) « Game Show Problem », sur Internet Archive (consulté le ).
- Le texte original était « Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, " Do you want to pick door No. 2? " Is it to your advantage to switch your choice? »
- (en)Vázsonyi told Erdös about the Monty Hall dilemma. “I told Erdös that the answer was to switch,” said Vázsonyi, “and fully expected to move to the next subject. But Erdös, to my surprise, said, ‘No, that is impossible. It should make no difference.’ At this point I was sorry I brought up the problem, because it was my experience that people get excited and emotional about the answer, and I end up with an unpleasant situation.” http://archive.vector.org.uk/art10011640.
- (en)Gnedin, Sasha « The Mondee Gills Game ». The Mathematical Intelligencer, 2011 (lire en ligne[PDF]).
- Pour la Science no 336, octobre 2005.
- Voir en ligne cet article.
- « Sweeth Tooth - Ian McEwan ».
- « Monty Hall », sur xkcd (consulté le )
Annexes[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- Le problème de Monty Hall, Denis van Waerebeke, Cédric Piktoroff (réalisation), dans Voyages au pays des maths sur Arte (, 10 minutes) Consulté le .
- « Le problème de Monty Hall », Apprendre en ligne, site pour jouer au problème.
- « Le paradoxe de Monty Hall », Les sorciers de Salem, Site d'activités mathématiques pour tous du Laboratoire de Mathématiques Raphaël Salem, (CNRS, Université de Rouen Normandie).