Géode (géométrie)


En mathématiques, une géode est un polyèdre convexe inscrit dans une sphère dont il réalise une approximation. Malgré les apparences, et sauf exceptions, ses faces ne sont pas rigoureusement identiques, et ses arêtes n’ont pas toutes la même longueur. Ces solides sont utilisés comme modèles pour certaines constructions architecturales : les dômes géodésiques.
Présentation rapide[modifier | modifier le code]
Géode par triangulation[modifier | modifier le code]
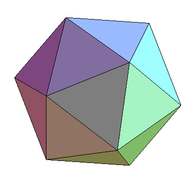
La plupart des géodes sont bâties sur le principe suivant : on part d'un icosaèdre.
|
Chacun des sommets de l'icosaèdre est commun à cinq facettes triangulaires, adjacentes deux à deux, et cinq arêtes (côtés des facettes) partent de chacun de ces sommets.
Chaque facette de l'icosaèdre est un triangle équilatéral, que l'on va subdiviser en triangles plus petits qui sont ensuite déformés (par projection radiale) pour être amenés sur la sphère circonscrite à l'icosaèdre. Voici trois exemples de géodes, correspondant chacun à une subdivision différente :

|

|

|
Dans le premier exemple, on a divisé les arêtes des faces de l'icosaèdre en deux segments. Dans le second, les arêtes ont été divisées en trois. Enfin, dans le dernier, elles ont été divisées en dix segments. C'est d'ailleurs sur ce dernier modèle qu'est bâtie la Géode de la Cité des sciences et de l'industrie de la Villette.
Pour repérer l'emplacement des sommets de l'icosaèdre initial, il suffit de trouver les endroits où 5 petits triangles (au lieu de 6) partagent un même sommet.
Géode en nid d'abeille[modifier | modifier le code]
On peut également concevoir des géodes en nid d'abeille en prenant le polyèdre dual des géodes obtenues par triangulation.
|
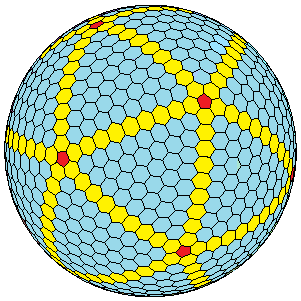
Dans la figure ci-dessus (qui est la figure agrandie du polyèdre dual de la géode du dernier exemple précédent basé sur une subdivision en 10 segments), la sphère semble pavée d'hexagones. Mais une observation attentive permet de découvrir que parmi ces hexagones se cachent en fait douze pentagones correspondant aux sommets de l'icosaèdre initial. Il est en effet impossible de recouvrir une sphère en n'utilisant que des hexagones, comme le montre la relation d'Euler entre nombres de faces, d'arêtes et de sommets d'un polyèdre, quel qu'il soit.
Sur la figure, trois de ces 12 pentagones sont bien visibles (en rouge), un quatrième, peu visible, se trouve près du bord de la figure, dans la direction « onze heures » (que marquerait la petite aiguille d'une montre), enfin un cinquième se cache sur le rebord de la figure, à « trois heures et demie ».
Principes de la construction géométrique d'une géode[modifier | modifier le code]
Les dômes géodésiques sont des structures basées sur la division des faces d'un polyèdre régulier dont les faces sont constituées de triangles équilatéraux.
Il n'existe que 3 types de polyèdres réguliers possédant de telles faces équilatérales : le tétraèdre régulier (N = 3), l'octaèdre régulier (N = 4) et l'icosaèdre régulier (N = 5), la notation N utilisée ici représentant le nombre de faces (et aussi le nombre d'arêtes) qui partagent un même sommet.
La division des faces est définie par deux paramètres entiers a et b, positifs ou nuls.
Le premier paramètre a doit être strictement positif.
Le second paramètre b peut être nul mais ne doit pas être supérieur à a.
Une fois choisies les valeurs de N puis de a et de b, la construction du dôme correspondant, que par la suite nous noterons « Géode M-a-b » (notation où le M doit être remplacé par III, IV ou V, selon la valeur en chiffres romains du nombre N), se déroule en 6 étapes, que nous allons expliquer en détail en privilégiant le cas N = 5 (qui correspond à l'immense majorité des géodes) et en l'illustrant dans les 3 cas suivants : , puis et enfin
Remarque : les figures qui précèdent correspondent, en utilisant la notation expliquée ci-dessus, aux géodes suivantes :
- dans l'introduction : la géode V-3-1 et sa duale (en rotation) ;
- au paragraphe 1.1 : la géode V-1-0 (icosaèdre) puis les géodes V-2-0, V-3-0 et V-10-0 ;
- au paragraphe 1.2 : la géode V-10-0 duale.
À partir d'un icosaèdre régulier[modifier | modifier le code]
Étape n° 1[modifier | modifier le code]

On construit un polyèdre régulier (R) correspondant à la valeur de N.
Étape n° 2[modifier | modifier le code]

- On choisit l'une des faces du polyèdre (R) puis l'une des arêtes de cette face (qui est toujours un triangle équilatéral). Soit AB l'arête choisie et C le sommet opposé à cette arête sur la face choisie.
- On divise alors le segment AB en (a + b) segments de longueur égale et l'on numérote tous les points ainsi définis : le point A reçoit le no 0, le point suivant le no 1, le suivant le no 2, etc. et le dernier, c'est-à-dire le point B, le no a + b. Soient les points ainsi obtenus.
- On trace ensuite le segment .
- Enfin, on trace tous les segments parallèles à et passant par chacun des points , sans toutefois dépasser les limites de la face ABC.
Étape n° 3[modifier | modifier le code]

- On répète la même opération en changeant respectivement l'arête AB et le sommet C, en BC et A, puis en CA et B ; on obtient ainsi un triple réseau de segments parallèles et équidistants faisant entre eux des angles de 60° et délimitant donc des petits triangles équilatéraux dont certains (sauf si le paramètre b vaut 0) sont incomplets. Ce sont les sommets de ces petits triangles qui vont servir à construire le dôme géodésique, y compris ceux qui sont situés juste à cheval sur l'une des arêtes de la face ABC.
- Bien entendu, il faut répéter les opérations décrites aux étapes 2 et 3 pour toutes les faces du polyèdre (R). Rappelons que le tétraèdre possède 4 faces, l'octaèdre 8 faces et l'icosaèdre 20 faces.
Étape n° 4[modifier | modifier le code]
- Soit O le centre de la sphère (S) circonscrite au polyèdre (R). Par la projection radiale de centre O, on projette sur la sphère (S) l'ensemble des réseaux obtenus ou, plus exactement, les sommets des petits triangles équilatéraux qu'aux étapes nos 2 et 3, on a obtenus sur chacune des faces de (R).

Étape n° 5[modifier | modifier le code]
- Pour former les arêtes du dôme géodésique V-a-b, on doit relier les divers sommets obtenus à l’étape précédente : toutefois, il ne faut relier entre eux que les sommets qui sont la projection de sommets appartenant à un même petit triangle équilatéral (voir étape no 3).

Étape n° 6[modifier | modifier le code]
Les arêtes obtenues à l'étape précédente forment des triangles sphériques, qui sont la projection radiale des petits triangles équilatéraux résultant de la division des faces du polyèdre initial (R).
- Pour achever le tracé de la géode V-a-b, il suffit d'effacer la trace de toutes les opérations effectuées aux étapes nos 1 à 4 : les sommets des triangles sphériques restants sont les sommets de la géode ; ces sommets, reliés deux à deux, dessinent l'ensemble des sommets et des faces de la géode V-a-b.

- Si au lieu de la géode normale, on souhaite construire la géode duale correspondante, il faut déterminer sur la sphère (S) le centre de chacun de ces triangles sphériques (qui sont donc « en face » des centres des faces de la géode V-a-b normale,) et si les points-centres ainsi obtenus correspondent à des faces adjacentes de la géode normale, on doit joindre ces points deux à deux pour former les arêtes de la géode duale. L'ensemble de ces arêtes dessinent des polygones qui sont les faces de la géode duale ; ces faces sont des hexagones, sauf douze d'entre elles qui sont des pentagones réguliers dont les centres sont situés « en face » des douze sommets du polyèdre générateur (R).
Il faut bien sûr effacer le tracé de la géode normale quand on a fini de tracer les arêtes de la géode duale.

À partir d'un octaèdre régulier[modifier | modifier le code]

Si l'on choisit comme polyèdre de départ (R) un octaèdre régulier (correspondant pour N à la valeur 4).
la construction exposée ci-dessus conduit à l'étape no 6 aux résultats suivants :


À partir d'un tétraèdre régulier[modifier | modifier le code]

Si l'on choisit enfin comme polyèdre de départ (R) un tétraèdre régulier (correspondant pour N à la valeur 3).
la même construction conduit à l'étape no 6 aux résultats suivants :


Quelques remarques géométriques[modifier | modifier le code]
Lorsque le paramètre b est nul ou égal au paramètre a, la géode (normale ou duale) possède toutes les propriétés de symétrie de son polyèdre générateur ; par exemple, pour l'icosaèdre : 15 plans de symétrie (passant par deux arêtes opposées), 10 rotations d'ordre 3 (rotation de 120° autour d'un axe passant par le centre de l'une des 20 faces) et 6 rotations d'ordre 5 (rotation de 72° autour d'un axe passant par deux sommets opposés)

En revanche, lorsque les paramètres a et b sont différents et tous deux positifs, la géode perd ses plans de symétrie et il existe donc deux formes de géodes de type N-a-b, qui sont énantiomorphes (c'est-à-dire symétriques l'une de l'autre dans un miroir, sans être superposables) ; pour s'en convaincre, il suffit de permuter les lettres A et B dans les explications données ci-dessus aux étapes nos 2 et 3 et d'examiner attentivement les figures correspondantes (dans le cas V-5-3) ou la figure ci-dessous :
- les triangles sphériques obtenus à l'étape no 5 paraissent être équilatéraux (du moins quand le polyèdre générateur est un icosaèdre) mais ils ne le sont pas (leurs angles ne sont jamais tous égaux) et leurs longueurs ne le sont que dans quelques rares cas particuliers ;
- de même, les hexagones obtenus dans la construction des géodes duales paraissent être réguliers mais ils ne le sont généralement pas (toutefois ils le sont lorsque a = b = 1, quel que soit N) ;
- selon une conjecture émise par Joseph D. Clinton mais qui reste à démontrer, il serait possible de déplacer légèrement les sommets du réseau triangulé décrit aux étapes nos 2 et 3 de façon que les arêtes des dômes N-a-b duaux soient toutes de longueurs égales. J. D. Clinton base sa conviction sur le fait que l'on a découvert l'existence de tels dômes « régularisés » pour toutes les combinaisons de a et de b suivantes :
- a + b < 4
- a = 4 et b = 0
- a = 2 et b = 2
- a = 5 et b = 0
- et enfin<
- a = 3 et b = 3
- avec N quelconque (égal à 3, 4 ou 5).
Si l'on choisit et , la géode V-1-0 normale obtenue est identique au polyèdre (R) générateur de départ. Quant à la géode V-1-0 duale, c'est le polyèdre régulier dual du même polyèdre ; c'est donc, selon la valeur de N, un dodécaèdre régulier (si ), un cube (si ) ou un tétraèdre régulier (si ).
La quantité que l'on convient d'appeler la « densité » d'une géode est intéressante car elle correspond au rapport de la surface des faces triangulaires du polyèdre (R) à la surface des petits triangles obtenus dans la division des faces. Elle intervient notamment dans le formulaire qui donne, en fonction de N, a et b, le nombre de faces F, d'arêtes A et de sommets S des dômes géodésiques normaux et duals.
Les arêtes d'un dôme géodésique normal (G) forment une triangulation de Delaunay de l'ensemble de ses sommets ; en outre, le dôme géodésique dual du même dôme (G) constitue une partition de la sphère (S) mais il ne correspond pas rigoureusement au diagramme de Voronoï des sommets du dôme (G), notamment pour les faibles valeurs de la densité .
Il n'est pas mathématiquement illogique de s'intéresser encore à un autre type de dômes géodésiques, ceux que l'on pourrait obtenir à partir d'une division (partition) des faces d'un autre polyèdre régulier, le cube ; cette division consisterait à découper chacune des six faces carrées du cube en mini-carrés. Pour construire de tels dômes « quadrangulés », il suffirait, à l'étape 2 décrite ci-dessus, de diviser l'une des deux diagonales BD d'une face ABCD (carrée) du cube en segments de longueur égale, puis de relier le sommet C au point et enfin de tracer tous les segments parallèles à et passant par les points , de la diagonale, sans dépasser les limites de la face carrée ABCD, puis, passant à l'étape 3, de faire une construction analogue avec la diagonale AC et le sommet B, et enfin de reproduire le quadrillage ainsi obtenu sur chacune des 5 autres faces du cube. Pour ces dômes, la « densité », rapport de la surface des faces du cube à la surface des petits carrés obtenus dans la division des faces, vaudrait .
Nota : le formulaire qui suit n'inclut pas le cas particulier des géodes « quadrangulées »
Formulaire[modifier | modifier le code]
Pour calculer les nombres F, A et S représentant les nombres de faces, d'arêtes et de sommets d'un dôme géodésique de paramètres N, a et b, il faut commencer par calculer les nombres f et D (qui représentent respectivement le nombre de faces du polyèdre régulier générateur (R) et la « densité » de la division des faces de ce polyèdre) à l'aide des deux formules préliminaires suivantes :
- et
On peut ensuite calculer :
- dans le cas des dômes géodésiques « normaux » :
- ,
et
- dans le cas des dômes géodésiques « duals » :
- ,
et
Détails complémentaires :
- les faces des dômes normaux sont toutes d'ordre 3 (ce sont des triangles) tandis que leurs sommets sont de deux types : ceux d'ordre 6 (auxquels aboutissent 6 arêtes) et ceux d'ordre N. Leurs nombres respectifs valent :
- et
- les sommets des dômes duals sont tous d'ordre 3 (3 arêtes y aboutissent) tandis que leurs faces sont de deux types : celles d'ordre 6 (hexagones) et celles d'ordre N (polygones à N côtés). Leurs nombres respectifs valent :
- et
- la droite portant le segment fait avec la hauteur relative au côté AB de la face ABC du polyèdre régulier (R) un angle dont le sinus et la tangente valent respectivement :
- et
Autres exemples de structures géode[modifier | modifier le code]
Balles et ballons[modifier | modifier le code]
Une géode V-1-1 duale a exactement la structure des ballons de football en usage dans les compétitions officielles : sur ces ballons, les 12 pentagones sont teints en noir tandis que les 20 hexagones sont teints en blanc.
Les balles de golf sont creusées de petits alvéoles dont le nombre, la forme et la position peuvent améliorer les performances des joueurs ; parmi les balles de golf professionnelles, on rencontre fréquemment des balles dont la disposition des alvéoles circulaires reproduit celle des faces (hexagones et pentagones) d'une géode V-6-0 duale.
Molécules et Virus[modifier | modifier le code]
Certains composés organiques remarquables tels que les C60 dont la structure est proche des géodes V-1-1 ont été baptisés fullerènes en hommage à R. B. Fuller ; on les appelle aussi parfois « footballènes ».
La majorité des virus sont des « virus icosaédraux » (en anglais « icosahedral viruses ») ou plus exactement des « virus à nucléocapside icosaédrale » : leur particularité tient à leur structure qui, très proche de celle d'un dôme géodésique, normal ou dual (sans toutefois la projection radiale sur la sphère (S)), leur confère une grande stabilité. Ils correspondent toujours à N = 5 et le plus souvent à des valeurs faibles de a et de b.
Parmi ces nombreux virus, on peut citer ceux des hépatites A, B, C et E, celui de la poliomyélite, celui du sida (HIV-1), celui de la fièvre jaune, celui de la variole, celui de la fièvre aphteuse, le virus habituel de la bronchiolite (VRS), ceux des verrues communes et plantaires (Papillomavirus HPV-3 et HPV-1), celui de la rubéole ou encore celui du « rhume de cerveau » ; mentionnons aussi le groupe des 8 virus dits herpesviridae qui possèdent tous la structure V-5-0 et qui peuvent induire différentes maladies humaines : varicelle, zona, mononucléose infectieuse, herpès labial, herpès néonatal et MST telles que l'herpès génital simple et l'herpès à cytomégalovirus.
Certains de ces virus sont « twisted » et correspondent donc à la classe III de Fuller : par exemple le Polyomavirus et le Papillomavirus qui sont du type V-2-1. On connaît même un virus de type V-10-7 (celui qui infeste l'algue Phaeocystis pouchetii).





























