Les transformations de Landen transforment une intégrale elliptique (ou une fonction elliptique jacobienne ) en une autre intégrale elliptique (ou une autre fonction elliptique jacobienne) de même forme, mais avec des variables différentes. Les transformations croissantes augmentent le module des fonctions elliptiques tandis que les transformations décroissantes le diminuent. Elles permettent d'effectuer plus rapidement les calculs numériques des fonctions elliptiques.
Cette transformation est l'œuvre initiale du mathématicien anglais John Landen (1719-1790) qui proposa en 1775 un changement de variable très réussi pour les intégrales et fonctions elliptiques.[ 1]
Il a pu montrer que la longueur d'un arc d'hyperbole pouvait être exprimée par les longueurs des arcs de deux ellipses différentes. Chacune d’elles présente une excentricité qui peut être identifiée au module elliptique. La relation particulière entre les excentricités des deux ellipses que Landen découvrit plus tard porte son nom.
Cette transformation a été redécouverte indépendamment par Carl Friedrich Gauss .[ 2] Joseph-Louis Lagrange , Adrien-Marie Legendre et Gauss .[ 3] lemniscate [ 4] Niels Henrik Abel et Charles Gustave Jacob Jacobi dans leur développement des fonctions elliptiques.
Landen a découvert une nouvelle façon de calculer, et pas seulement les fonctions elliptiques. Son idée principale, selon laquelle la fonction calculée peut être représentée par une fonction de la même forme mais avec d'autres paramètres qui tendent vers certaines limites lors de la récursion, a ensuite été largement utilisée en mathématiques computationnelles. Cette transformation modulaire joue un rôle important dans les mathématiques modernes.[ 5]
Les intégrales elliptiques de première , deuxième et troisième espèce s'écrivent respectivement souvent ainsi :[ A 1]
F
(
φ
,
k
)
=
F
(
sin
φ
;
k
)
=
F
(
φ
|
k
2
)
=
F
(
φ
∖
arcsin
k
)
=
∫
0
φ
d
θ
1
−
k
2
sin
2
θ
=
∫
t
=
sin
θ
=
0
sin
φ
d
t
(
1
−
t
2
)
(
1
−
k
2
t
2
)
{\displaystyle F\left(\varphi ,k\right)=F\left(\sin \varphi ;k\right)=F\left(\varphi |k^{2}\right)=F\left(\varphi \setminus \arcsin k\right)=\int _{0}^{\varphi }{\frac {\mathrm {d} \theta }{\sqrt {1-k^{2}\sin ^{2}\theta }}}=\int _{t=\sin \theta =0}^{\sin \varphi }{\frac {\mathrm {d} t}{\sqrt {\left(1-t^{2}\right)\left(1-k^{2}t^{2}\right)}}}}
E
(
φ
,
k
)
=
E
(
sin
φ
;
k
)
=
E
(
φ
|
k
2
)
=
E
(
φ
∖
arcsin
k
)
=
∫
0
φ
1
−
k
2
sin
2
θ
d
θ
=
∫
t
=
sin
θ
=
0
sin
φ
1
−
k
2
t
2
1
−
t
2
d
t
{\displaystyle E(\varphi ,k)=E(\sin \varphi ;k)=E(\varphi |k^{2})=E(\varphi \setminus \arcsin k)=\int _{0}^{\varphi }{\sqrt {1-k^{2}\sin ^{2}\theta }}\,\mathrm {d} \theta =\int _{t=\sin \theta =0}^{\sin \varphi }{\frac {\sqrt {1-k^{2}t^{2}}}{\sqrt {1-t^{2}}}}\,\mathrm {d} t}
Π
(
n
;
φ
,
k
)
=
Π
(
n
;
sin
φ
;
k
)
=
Π
(
n
;
φ
|
k
2
)
=
Π
(
n
;
φ
∖
arcsin
k
)
=
∫
0
φ
1
1
−
n
sin
2
θ
d
θ
1
−
k
2
sin
2
θ
=
∫
t
=
sin
θ
=
0
sin
φ
1
1
−
n
t
2
d
t
(
1
−
t
2
)
(
1
−
k
2
t
2
)
{\displaystyle \Pi (n;\varphi ,k)=\Pi (n;\sin \varphi ;k)=\Pi (n;\varphi |k^{2})=\Pi (n;\varphi \setminus \arcsin k)=\int _{0}^{\varphi }{\frac {1}{1-n\sin ^{2}\theta }}{\frac {\mathrm {d} \theta }{\sqrt {1-k^{2}\sin ^{2}\theta }}}=\int _{t=\sin \theta =0}^{\sin \varphi }{\frac {1}{1-nt^{2}}}{\frac {\mathrm {d} t}{\sqrt {\left(1-t^{2}\right)\left(1-k^{2}t^{2}\right)}}}}
La forme de la première intégrale est appelée la forme trigonométrique ou la forme canonique de Legendre ; la forme de la deuxième intégrale est appelée la forme jacobienne . On appelle
k
∈
[
0
;
1
]
{\displaystyle k\in [0;1]}
module ,
m
=
k
2
{\displaystyle m=k^{2}}
paramètre ,
k
′
=
1
−
k
2
{\displaystyle k'={\sqrt {1-k^{2}}}}
comodule ,
arcsin
k
{\displaystyle \arcsin k}
angle modulaire
φ
{\displaystyle \varphi }
amplitude et
n
{\displaystyle n}
caractéristique . Si
φ
{\displaystyle \varphi }
incomplète , si
φ
=
π
/
2
{\displaystyle \varphi =\pi /2}
complète .
Les intégrales elliptiques complètes de première et deuxième espèce sont respectivement :
K
(
k
)
=
F
(
π
2
,
k
)
{\displaystyle K\left(k\right)=F\left({\frac {\pi }{2}},k\right)}
E
(
k
)
=
E
(
π
2
,
k
)
{\displaystyle E\left(k\right)=E\left({\frac {\pi }{2}},k\right)}
On définit aussi
K
′
(
k
)
=
K
(
k
′
)
{\displaystyle K'\left(k\right)=K\left(k'\right)}
E
′
(
k
)
=
E
(
k
′
)
{\displaystyle E'\left(k\right)=E\left(k'\right)}
On appelle fonction amplitude de Jacobi la fonction réciproque de
F
{\displaystyle F}
a
m
{\displaystyle {\rm {am}}}
u
=
F
(
φ
,
k
)
⇔
φ
=
a
m
(
u
,
k
)
{\displaystyle u=F\left(\varphi ,k\right)\Leftrightarrow \varphi ={\rm {am}}(u,k)}
Les trois fonctions jacobiennes de base (1827) sont :
la fonction sinus de Jacobi :
s
n
(
u
,
k
)
=
sin
(
a
m
(
u
,
k
)
)
{\displaystyle {\rm {sn}}(u,k)=\sin({\rm {am}}(u,k))}
la fonction cosinus de Jacobi :
c
n
(
u
,
k
)
=
cos
(
a
m
(
u
,
k
)
)
{\displaystyle {\rm {cn}}(u,k)=\cos({\rm {am}}(u,k))}
la fonction delta de Jacobi :
d
n
(
u
,
k
)
=
Δ
1
−
k
2
s
n
(
u
,
k
)
2
{\displaystyle {\rm {dn}}(u,k)=\Delta {\sqrt {1-k^{2}{\rm {sn}}(u,k)^{2}}}}
Gudermann (1838), puis Glaisher (1882) introduiront les neuf autres fonctions jacobiennes :
n
s
(
u
,
k
)
=
1
s
n
(
u
,
k
)
,
n
c
(
u
,
k
)
=
1
c
n
(
u
,
k
)
,
n
d
(
u
,
k
)
=
1
d
n
(
u
,
k
)
,
s
c
(
u
,
k
)
=
s
n
(
u
,
k
)
c
n
(
u
,
k
)
,
c
s
(
u
,
k
)
=
c
n
(
u
,
k
)
s
n
(
u
,
k
)
,
s
d
(
u
,
k
)
=
s
n
(
u
,
k
)
d
n
(
u
,
k
)
,
d
s
(
u
,
k
)
=
d
n
(
u
,
k
)
s
n
(
u
,
k
)
,
c
d
(
u
,
k
)
=
c
n
(
u
,
k
)
d
n
(
u
,
k
)
,
d
c
(
u
,
k
)
=
d
n
(
u
,
k
)
c
n
(
u
,
k
)
.
{\displaystyle {\begin{aligned}{\rm {ns}}(u,k)&={\frac {1}{{\rm {sn}}(u,k)}},\quad {\rm {nc}}(u,k)={\frac {1}{{\rm {cn}}(u,k)}},\quad {\rm {nd}}(u,k)={\frac {1}{{\rm {dn}}(u,k)}},\\{\rm {sc}}(u,k)&={\frac {{\rm {sn}}(u,k)}{{\rm {cn}}(u,k)}},\quad {\rm {cs}}(u,k)={\frac {{\rm {cn}}(u,k)}{{\rm {sn}}(u,k)}},\\{\rm {sd}}(u,k)&={\frac {{\rm {sn}}(u,k)}{{\rm {dn}}(u,k)}},\quad {\rm {ds}}(u,k)={\frac {{\rm {dn}}(u,k)}{{\rm {sn}}(u,k)}},\\{\rm {cd}}(u,k)&={\frac {{\rm {cn}}(u,k)}{{\rm {dn}}(u,k)}},\quad {\rm {dc}}(u,k)={\frac {{\rm {dn}}(u,k)}{{\rm {cn}}(u,k)}}.\end{aligned}}}
Jacobi a aussi introduit :
la coamplitude :
c
o
a
m
(
u
,
k
)
=
a
m
(
K
−
u
)
(
u
,
k
)
=
π
/
2
−
a
m
(
u
,
k
)
{\displaystyle {\rm {coam}}(u,k)={\rm {am}}(K-u)(u,k)=\pi /2-{\rm {am}}(u,k)}
[ A 2]
la fonction epsilon de Jacobi [ 6]
E
(
u
,
k
)
=
∫
0
u
dn
2
(
t
,
k
)
d
t
{\displaystyle {\mathcal {E}}(u,k)=\int _{0}^{u}\operatorname {dn} ^{2}(t,k)\,\mathrm {d} t}
la fonction zn de Jacobi :
zn
(
u
,
k
)
=
∫
0
u
[
dn
(
t
,
k
)
2
−
E
(
k
)
K
(
k
)
]
d
t
{\displaystyle \operatorname {zn} (u,k)=\int _{0}^{u}\left[\operatorname {dn} (t,k)^{2}-{\frac {E(k)}{K(k)}}\right]\,\mathrm {d} t}
la fonction zeta de Jacobi :
Z
(
φ
,
k
)
=
zn
(
F
(
φ
,
k
)
,
k
)
{\displaystyle Z(\varphi ,k)=\operatorname {zn} (F(\varphi ,k),k)}
On a aussi[ A 3]
le gudermannian :
g
d
(
u
)
=
a
m
(
u
,
1
)
=
2
arctan
e
u
−
π
/
2
{\displaystyle {\rm {gd}}(u)={\rm {am}}(u,1)=2\arctan \mathrm {e} ^{u}-\pi /2}
la fonction correspondant à
s
n
{\displaystyle {\rm {sn}}}
s
g
(
u
)
=
sin
(
g
d
(
u
)
)
{\displaystyle {\rm {sg}}(u)=\sin({\rm {gd}}(u))}
la fonction correspondant à
c
n
{\displaystyle {\rm {cn}}}
c
g
(
u
)
=
cos
(
g
d
(
u
)
)
{\displaystyle {\rm {cg}}(u)=\cos({\rm {gd}}(u))}
Transformations de Landen des intégrales elliptiques de première espèce [ modifier | modifier le code ] Au sens large, la transformation de Landen désigne une transformation reposant sur le principe selon lequel la fonction calculée peut être représentée par une fonction de la même forme mais avec d'autres paramètres qui tendent vers certaines limites lors de la récursion ; tandis que la transformation de Landen à proprement parlé désigne la transformation qui utilise le changement de variable que Landen a proposé[ 7]
Les transformations changent le module
k
=
k
0
{\displaystyle k=k_{0}}
k
1
{\displaystyle k_{1}}
k
−
1
{\displaystyle k_{-1}}
θ
=
θ
0
{\displaystyle \theta =\theta _{0}}
θ
1
{\displaystyle \theta _{1}}
θ
−
1
{\displaystyle \theta _{-1}}
pour la transformation de Landen :
sin
(
2
θ
n
+
1
−
θ
n
)
=
k
n
sin
θ
n
⇔
sin
θ
n
=
2
1
+
k
n
sin
θ
n
+
1
cos
θ
n
+
1
1
−
(
2
k
n
1
+
k
n
)
2
sin
2
θ
n
+
1
{\displaystyle \sin \left(2\theta _{n+1}-\theta _{n}\right)=k_{n}\sin \theta _{n}\quad \Leftrightarrow \quad \sin \theta _{n}={\frac {{\frac {2}{1+k_{n}}}\sin \theta _{n+1}\cos \theta _{n+1}}{\sqrt {1-\left({\frac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)^{2}\sin ^{2}\theta _{n+1}}}}}
pour la transformation gaussienne :
sin
θ
n
+
1
=
(
1
+
k
n
)
sin
θ
n
1
+
k
n
sin
2
θ
n
⇔
sin
θ
n
=
2
1
+
k
n
sin
θ
n
+
1
1
+
1
−
(
2
k
n
1
+
k
n
)
2
sin
2
θ
n
+
1
{\displaystyle \sin \theta _{n+1}={\frac {\left(1+k_{n}\right)\sin \theta _{n}}{1+k_{n}\sin ^{2}\theta _{n}}}\quad \Leftrightarrow \quad \sin \theta _{n}={\frac {{\frac {2}{1+k_{n}}}\sin \theta _{n+1}}{1+{\sqrt {1-\left({\frac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)^{2}\sin ^{2}\theta _{n+1}}}}}}
Ainsi, pour la transformation de Landen comme pour la transformation gaussienne, on a les relations suivantes (on pose :
k
0
′
=
k
′
{\displaystyle k'_{0}=k'}
{
k
n
+
1
=
2
k
n
1
+
k
n
=
2
1
−
k
n
′
2
4
1
+
1
−
k
n
′
2
,
k
n
+
1
′
=
1
−
k
n
1
+
k
n
=
1
−
1
−
k
n
′
2
1
+
1
−
k
n
′
2
⇔
k
n
−
1
=
1
−
1
−
k
n
2
1
+
1
−
k
n
2
=
1
−
k
n
′
1
+
k
n
′
,
k
n
−
1
′
=
2
1
−
k
n
2
4
1
+
1
−
k
n
2
=
2
k
n
′
1
+
k
n
′
{\displaystyle {\begin{cases}&k_{n+1}&={\frac {2{\sqrt {k_{n}}}}{1+k_{n}}}&={\frac {2{\sqrt[{4}]{1-k_{n}'^{2}}}}{1+{\sqrt {1-k_{n}'^{2}}}}},&k_{n+1}'&={\frac {1-k_{n}}{1+k_{n}}}&={\frac {1-{\sqrt {1-k_{n}'^{2}}}}{1+{\sqrt {1-k_{n}'^{2}}}}}\\\Leftrightarrow &k_{n-1}&={\frac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}&={\frac {1-k_{n}'}{1+k_{n}'}},&k_{n-1}'&={\frac {2{\sqrt[{4}]{1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}&={\frac {2{\sqrt {k_{n}'}}}{1+k_{n}'}}\end{cases}}}
Une transformation qui change
k
n
{\displaystyle k_{n}}
k
n
+
1
{\displaystyle k_{n+1}}
k
n
{\displaystyle k_{n}}
k
n
−
1
{\displaystyle k_{n-1}}
{
k
n
⩽
1
⇒
k
n
+
1
⩾
k
n
⇒
k
n
+
1
⩾
k
n
k
n
−
1
=
k
n
2
(
1
+
k
n
′
)
2
⇒
k
n
−
1
⩽
k
n
{\displaystyle {\begin{cases}k_{n}\leqslant 1\Rightarrow k_{n+1}\geqslant {\sqrt {k_{n}}}&\Rightarrow k_{n+1}\geqslant k_{n}\\k_{n-1}={\frac {k_{n}^{2}}{\left(1+k_{n}'\right)^{2}}}&\Rightarrow k_{n-1}\leqslant k_{n}\end{cases}}}
Commençons par vérifier la réciprocité de :
sin
(
2
θ
n
+
1
−
θ
n
)
=
k
n
sin
θ
n
⇔
sin
θ
n
=
2
1
+
k
n
sin
θ
n
+
1
cos
θ
n
+
1
1
−
(
2
k
n
1
+
k
n
)
2
sin
2
θ
n
+
1
{\displaystyle \sin \left(2\theta _{n+1}-\theta _{n}\right)=k_{n}\sin \theta _{n}\quad \Leftrightarrow \quad \sin \theta _{n}={\frac {{\frac {2}{1+k_{n}}}\sin \theta _{n+1}\cos \theta _{n+1}}{\sqrt {1-\left({\frac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)^{2}\sin ^{2}\theta _{n+1}}}}}
On a :
sin
θ
n
=
sin
(
2
θ
n
+
1
)
1
+
k
n
2
+
2
k
n
cos
(
2
θ
n
+
1
)
{\displaystyle \sin \theta _{n}={\frac {\sin \left(2\theta _{n+1}\right)}{\sqrt {1+k_{n}^{2}+2k_{n}\cos \left(2\theta _{n+1}\right)}}}}
cos
θ
n
=
k
n
+
cos
(
2
θ
n
+
1
)
1
+
k
n
2
+
2
k
n
cos
(
2
θ
n
+
1
)
{\displaystyle \cos \theta _{n}={\frac {k_{n}+\cos \left(2\theta _{n+1}\right)}{\sqrt {1+k_{n}^{2}+2k_{n}\cos \left(2\theta _{n+1}\right)}}}}
tan
θ
n
=
sin
(
2
θ
n
+
1
)
k
n
+
cos
(
2
θ
n
+
1
)
{\displaystyle \tan \theta _{n}={\frac {\sin \left(2\theta _{n+1}\right)}{k_{n}+\cos \left(2\theta _{n+1}\right)}}}
En multipliant cette dernière égalité par
cos
θ
n
[
k
n
+
cos
(
2
θ
n
+
1
)
]
{\displaystyle \cos \theta _{n}\left[k_{n}+\cos \left(2\theta _{n+1}\right)\right]}
sin
(
2
θ
n
+
1
−
θ
n
)
=
k
n
sin
θ
n
{\displaystyle \sin \left(2\theta _{n+1}-\theta _{n}\right)=k_{n}\sin \theta _{n}}
k
n
⩽
1
⇒
2
θ
n
+
1
−
θ
n
⩽
θ
n
⇒
θ
n
+
1
⩽
θ
n
{\displaystyle k_{n}\leqslant 1\Rightarrow 2\theta _{n+1}-\theta _{n}\leqslant \theta _{n}\Rightarrow \theta _{n+1}\leqslant \theta _{n}}
[ 8]
Les grandeurs apparaissant dans l'intégrale elliptique de première espèce sont :
1
−
k
n
2
sin
2
θ
n
=
1
−
sin
2
(
2
θ
n
+
1
−
θ
n
)
=
cos
(
2
θ
n
+
1
−
θ
n
)
=
1
+
k
n
cos
(
2
θ
n
+
1
)
1
+
k
n
2
+
2
k
n
cos
(
2
θ
n
+
1
)
{\displaystyle {\sqrt {1-k_{n}^{2}\sin ^{2}\theta _{n}}}={\sqrt {1-\sin ^{2}(2\theta _{n+1}-\theta _{n})}}=\cos \left(2\theta _{n+1}-\theta _{n}\right)={\frac {1+k_{n}\cos \left(2\theta _{n+1}\right)}{\sqrt {1+k_{n}^{2}+2k_{n}\cos \left(2\theta _{n+1}\right)}}}}
d
θ
n
=
cos
2
θ
n
d
tan
θ
n
=
2
[
1
+
k
n
cos
(
2
θ
n
+
1
)
]
1
+
k
n
2
+
2
k
n
cos
(
2
θ
n
+
1
)
d
θ
n
+
1
{\displaystyle \mathrm {d} \theta _{n}=\cos ^{2}\theta _{n}\,\mathrm {d} \tan \theta _{n}={\frac {2\left[1+k_{n}\cos \left(2\theta _{n+1}\right)\right]}{1+k_{n}^{2}+2k_{n}\cos \left(2\theta _{n+1}\right)}}\mathrm {d} \theta _{n+1}}
Ainsi :
d
θ
n
1
−
k
n
2
sin
2
θ
n
=
2
1
+
k
n
d
θ
n
+
1
1
−
k
n
+
1
2
sin
2
θ
n
+
1
{\displaystyle {\mathrm {d} \theta _{n} \over {\sqrt {1-k_{n}^{2}\sin ^{2}\theta _{n}}}}={\frac {2}{1+k_{n}}}{\frac {\mathrm {d} \theta _{n+1}}{\sqrt {1-k_{n+1}^{2}\sin ^{2}\theta _{n+1}}}}}
Calculons l'amplitude
φ
n
+
1
L
{\displaystyle \varphi _{n+1}^{L}}
φ
0
L
=
φ
{\displaystyle \varphi _{0}^{L}=\varphi }
sin
2
φ
n
L
=
1
−
cos
2
(
2
φ
n
+
1
L
)
1
+
k
n
2
+
2
k
n
cos
(
2
φ
n
+
1
L
)
{\displaystyle \sin ^{2}\varphi _{n}^{L}={\frac {1-\cos ^{2}(2\varphi _{n+1}^{L})}{1+k_{n}^{2}+2k_{n}\cos(2\varphi _{n+1}^{L})}}}
⇒
cos
2
(
2
φ
n
+
1
L
)
+
2
k
n
sin
2
φ
n
L
cos
(
2
φ
n
+
1
L
)
+
k
n
2
sin
2
φ
n
L
−
1
+
sin
2
φ
n
L
=
0
{\displaystyle \Rightarrow \cos ^{2}(2\varphi _{n+1}^{L})+2k_{n}\sin ^{2}\varphi _{n}^{L}\cos(2\varphi _{n+1}^{L})+k_{n}^{2}\sin ^{2}\varphi _{n}^{L}-1+\sin ^{2}\varphi _{n}^{L}=0}
⇒
cos
(
2
φ
n
+
1
L
)
=
−
k
n
sin
2
φ
n
L
±
k
n
2
sin
4
φ
n
L
−
k
n
2
sin
2
φ
n
L
+
1
−
sin
2
φ
n
L
∈
[
−
1
;
+
1
]
{\displaystyle \Rightarrow \cos(2\varphi _{n+1}^{L})=-k_{n}\sin ^{2}\varphi _{n}^{L}\pm {\sqrt {k_{n}^{2}\sin ^{4}\varphi _{n}^{L}-k_{n}^{2}\sin ^{2}\varphi _{n}^{L}+1-\sin ^{2}\varphi _{n}^{L}}}\in \left[-1;+1\right]}
⇒
cos
(
2
φ
n
+
1
L
)
=
−
k
n
sin
2
φ
n
L
+
cos
φ
n
L
1
−
k
n
2
sin
2
φ
n
L
{\displaystyle \Rightarrow \cos(2\varphi _{n+1}^{L})=-k_{n}\sin ^{2}\varphi _{n}^{L}+\cos \varphi _{n}^{L}{\sqrt {1-k_{n}^{2}\sin ^{2}\varphi _{n}^{L}}}}
⇒
φ
n
+
1
L
=
arcsin
1
+
k
n
sin
2
φ
n
L
−
cos
φ
n
L
1
−
k
n
2
sin
2
φ
n
L
2
{\displaystyle \Rightarrow \varphi _{n+1}^{L}=\arcsin {\sqrt {\frac {1+k_{n}\sin ^{2}\varphi _{n}^{L}-\cos \varphi _{n}^{L}{\sqrt {1-k_{n}^{2}\sin ^{2}\varphi _{n}^{L}}}}{2}}}}
Calculons l'amplitude
φ
n
L
{\displaystyle \varphi _{n}^{L}}
φ
n
+
1
L
∈
[
φ
n
L
2
;
φ
n
L
]
⇔
φ
n
L
∈
[
φ
n
+
1
L
;
2
φ
n
+
1
L
]
{\displaystyle \varphi _{n+1}^{L}\in \left[{\frac {\varphi _{n}^{L}}{2}};\varphi _{n}^{L}\right]\Leftrightarrow \varphi _{n}^{L}\in \left[\varphi _{n+1}^{L};2\varphi _{n+1}^{L}\right]}
{
φ
n
+
1
L
∈
[
0
;
π
2
−
arccos
k
n
2
]
⇔
φ
n
L
∈
[
0
;
π
2
]
φ
n
+
1
L
∈
[
π
2
−
arccos
k
n
2
;
π
2
]
⇔
φ
n
L
∈
[
π
2
;
π
]
{\displaystyle {\begin{cases}\varphi _{n+1}^{L}\in \left[0;{\frac {\pi }{2}}-{\frac {\arccos k_{n}}{2}}\right]&\Leftrightarrow \varphi _{n}^{L}\in \left[0;{\frac {\pi }{2}}\right]\\\varphi _{n+1}^{L}\in \left[{\frac {\pi }{2}}-{\frac {\arccos k_{n}}{2}};{\frac {\pi }{2}}\right]&\Leftrightarrow \varphi _{n}^{L}\in \left[{\frac {\pi }{2}};\pi \right]\end{cases}}}
φ
n
L
=
arccos
k
n
+
cos
(
2
φ
n
+
1
L
)
1
+
k
n
2
+
2
k
n
cos
(
2
φ
n
+
1
L
)
=
arccos
1
−
(
1
+
k
n
+
1
′
)
sin
2
φ
n
+
1
L
1
−
k
n
+
1
2
sin
2
φ
n
+
1
L
{\displaystyle \varphi _{n}^{L}=\arccos {\frac {k_{n}+\cos \left(2\varphi _{n+1}^{L}\right)}{\sqrt {1+k_{n}^{2}+2k_{n}\cos \left(2\varphi _{n+1}^{L}\right)}}}=\arccos {\frac {1-\left(1+k'_{n+1}\right)\sin ^{2}\varphi _{n+1}^{L}}{\sqrt {1-k_{n+1}^{2}\sin ^{2}\varphi _{n+1}^{L}}}}}
Si on utilise la notation de l'intégrale elliptique avec un point-virgule, on est obligé de décomposer l'intégrale en tronçons ne dépassant pas
π
/
2
{\displaystyle \pi /2}
π
/
2
{\displaystyle \pi /2}
φ
n
L
∈
]
π
/
2
;
π
]
{\displaystyle \varphi _{n}^{L}\in \left]\pi /2;\pi \right]}
F
(
φ
n
L
,
k
n
)
=
2
K
(
k
n
)
−
F
(
π
−
φ
n
L
,
k
n
)
=
2
K
(
k
n
)
−
F
(
sin
φ
n
L
;
k
n
)
{\displaystyle F\left(\varphi _{n}^{L},k_{n}\right)=2K\left(k_{n}\right)-F\left(\pi -\varphi _{n}^{L},k_{n}\right)=2K\left(k_{n}\right)-F\left(\sin \varphi _{n}^{L};k_{n}\right)}
Si
k
n
{\displaystyle k_{n}}
k
n
+
1
′
{\displaystyle k_{n+1}'}
φ
n
L
{\displaystyle \varphi _{n}^{L}}
φ
n
+
1
L
{\displaystyle \varphi _{n+1}^{L}}
(
1
+
k
n
)
(
1
+
k
n
+
1
′
)
=
2
{\displaystyle \left(1+k_{n}\right)\left(1+k_{n+1}'\right)=2}
tan
(
φ
n
L
−
φ
n
+
1
L
)
=
k
n
+
1
′
tan
φ
n
+
1
L
{\displaystyle \tan \left(\varphi _{n}^{L}-\varphi _{n+1}^{L}\right)=k_{n+1}'\tan \varphi _{n+1}^{L}}
F
(
φ
n
L
,
k
n
)
=
2
1
+
k
n
F
(
φ
n
+
1
L
,
k
n
+
1
)
=
(
1
+
k
n
+
1
′
)
F
(
φ
n
+
1
L
,
k
n
+
1
)
{\displaystyle F\left(\varphi _{n}^{L},k_{n}\right)={\frac {2}{1+k_{n}}}F\left(\varphi _{n+1}^{L},k_{n+1}\right)=(1+k_{n+1}')F\left(\varphi _{n+1}^{L},k_{n+1}\right)}
La transformation de Landen peut donc être exprimée soit en fonction de son module elliptique
k
{\displaystyle k}
k
′
{\displaystyle k'}
En effet :
En réécrivant
sin
(
2
φ
n
+
1
L
−
φ
n
L
)
=
k
n
sin
φ
n
L
{\displaystyle \sin \left(2\varphi _{n+1}^{L}-\varphi _{n}^{L}\right)=k_{n}\sin \varphi _{n}^{L}}
sin
φ
n
+
1
L
cos
(
φ
n
+
1
L
−
φ
n
L
)
+
cos
φ
n
+
1
L
sin
(
φ
n
+
1
L
−
φ
n
L
)
=
k
n
sin
(
φ
n
L
−
φ
n
+
1
L
)
cos
φ
n
+
1
L
+
k
n
cos
(
φ
n
L
−
φ
n
+
1
L
)
sin
φ
n
+
1
L
{\displaystyle \sin \varphi _{n+1}^{L}\cos \left(\varphi _{n+1}^{L}-\varphi _{n}^{L}\right)+\cos \varphi _{n+1}^{L}\sin \left(\varphi _{n+1}^{L}-\varphi _{n}^{L}\right)=k_{n}\sin \left(\varphi _{n}^{L}-\varphi _{n+1}^{L}\right)\cos \varphi _{n+1}^{L}+k_{n}\cos \left(\varphi _{n}^{L}-\varphi _{n+1}^{L}\right)\sin \varphi _{n+1}^{L}}
et en divisant par
cos
φ
n
+
1
L
cos
(
φ
n
+
1
L
−
φ
n
L
)
{\displaystyle \cos \varphi _{n+1}^{L}\cos \left(\varphi _{n+1}^{L}-\varphi _{n}^{L}\right)}
tan
φ
n
+
1
L
−
tan
(
φ
n
L
−
φ
n
+
1
L
)
=
k
n
tan
(
φ
n
L
−
φ
n
+
1
L
)
+
k
n
tan
φ
n
+
1
L
{\displaystyle \tan \varphi _{n+1}^{L}-\tan \left(\varphi _{n}^{L}-\varphi _{n+1}^{L}\right)=k_{n}\tan \left(\varphi _{n}^{L}-\varphi _{n+1}^{L}\right)+k_{n}\tan \varphi _{n+1}^{L}}
ce qui donne :
tan
(
φ
n
L
−
φ
n
+
1
L
)
=
k
n
+
1
′
tan
φ
n
+
1
L
⇒
tan
φ
n
L
−
tan
φ
n
+
1
L
1
+
tan
φ
n
L
tan
φ
n
+
1
L
=
k
n
+
1
′
tan
φ
n
+
1
L
⇒
tan
φ
n
L
=
(
1
+
k
n
+
1
′
)
tan
φ
n
+
1
L
1
−
k
n
+
1
′
tan
2
φ
n
+
1
L
{\displaystyle \tan \left(\varphi _{n}^{L}-\varphi _{n+1}^{L}\right)=k_{n+1}'\tan \varphi _{n+1}^{L}\Rightarrow {\frac {\tan \varphi _{n}^{L}-\tan \varphi _{n+1}^{L}}{1+\tan \varphi _{n}^{L}\tan \varphi _{n+1}^{L}}}=k_{n+1}'\tan \varphi _{n+1}^{L}\Rightarrow \tan \varphi _{n}^{L}={\frac {\left(1+k_{n+1}'\right)\tan \varphi _{n+1}^{L}}{1-k_{n+1}'\tan ^{2}\varphi _{n+1}^{L}}}}
(
1
+
k
n
)
(
1
+
k
n
+
1
′
)
=
2
{\displaystyle \left(1+k_{n}\right)\left(1+k_{n+1}'\right)=2}
Commençons par vérifier la réciprocité de :
sin
θ
n
+
1
=
(
1
+
k
n
)
sin
θ
n
1
+
k
n
sin
2
θ
n
⇔
sin
θ
n
=
2
1
+
k
n
sin
θ
n
+
1
1
+
1
−
(
2
k
n
1
+
k
n
)
2
sin
2
θ
n
+
1
{\displaystyle \sin \theta _{n+1}={\frac {\left(1+k_{n}\right)\sin \theta _{n}}{1+k_{n}\sin ^{2}\theta _{n}}}\quad \Leftrightarrow \quad \sin \theta _{n}={\frac {{\frac {2}{1+k_{n}}}\sin \theta _{n+1}}{1+{\sqrt {1-\left({\frac {2{\sqrt {k}}_{n}}{1+k_{n}}}\right)^{2}\sin ^{2}\theta _{n+1}}}}}}
On a bien :
sin
θ
n
=
2
sin
θ
n
1
+
k
n
sin
2
θ
n
1
+
1
−
(
2
k
n
1
+
k
n
)
2
(
1
+
k
n
)
2
sin
2
θ
n
(
1
+
k
n
sin
2
θ
n
)
2
=
2
sin
θ
n
1
+
k
n
sin
2
θ
n
1
+
1
−
k
n
sin
2
θ
n
1
+
k
n
sin
2
θ
n
=
sin
θ
n
{\displaystyle \sin \theta _{n}={\frac {\frac {2\sin \theta _{n}}{1+k_{n}\sin ^{2}\theta _{n}}}{1+{\sqrt {1-\left({\frac {2{\sqrt {k}}_{n}}{1+k_{n}}}\right)^{2}{\frac {\left(1+k_{n}\right)^{2}\sin ^{2}\theta _{n}}{\left(1+k_{n}\sin ^{2}\theta _{n}\right)^{2}}}}}}}={\frac {\frac {2\sin \theta _{n}}{1+k_{n}\sin ^{2}\theta _{n}}}{1+{\frac {1-k_{n}\sin ^{2}\theta _{n}}{1+k_{n}\sin ^{2}\theta _{n}}}}}=\sin \theta _{n}}
Les grandeurs apparaissant dans l'intégrale elliptique de première espèce sont :
1
−
k
n
2
sin
2
θ
n
=
(
1
+
k
n
−
k
n
cos
2
θ
n
)
2
−
(
1
+
k
n
)
2
+
(
1
+
k
n
)
2
cos
2
θ
n
cos
θ
n
=
(
1
+
k
n
sin
2
θ
n
)
2
−
(
1
+
k
n
)
2
sin
2
θ
n
cos
θ
n
{\displaystyle {\sqrt {1-k_{n}^{2}\sin ^{2}\theta _{n}}}={\frac {\sqrt {\left(1+k_{n}-k_{n}\cos ^{2}\theta _{n}\right)^{2}-\left(1+k_{n}\right)^{2}+\left(1+k_{n}\right)^{2}\cos ^{2}\theta _{n}}}{\cos \theta _{n}}}={\frac {\sqrt {\left(1+k_{n}\sin ^{2}\theta _{n}\right)^{2}-\left(1+k_{n}\right)^{2}\sin ^{2}\theta _{n}}}{\cos \theta _{n}}}}
d
θ
n
+
1
=
d
sin
θ
n
+
1
cos
θ
n
+
1
=
(
1
+
k
n
sin
2
θ
n
)
(
1
+
k
n
)
cos
θ
n
−
2
k
n
(
1
+
k
n
)
sin
2
θ
n
cos
θ
n
cos
θ
n
+
1
(
1
+
k
n
sin
2
θ
n
)
2
d
θ
n
=
(
1
−
k
n
sin
2
θ
n
)
(
1
+
k
n
)
cos
θ
n
(
1
+
k
n
sin
2
θ
n
)
(
1
+
k
n
sin
2
θ
n
)
2
−
(
1
+
k
n
)
2
sin
2
θ
n
d
θ
n
{\displaystyle \mathrm {d} \theta _{n+1}={\frac {\mathrm {d} \sin \theta _{n+1}}{\cos \theta _{n+1}}}={\frac {\left(1+k_{n}\sin ^{2}\theta _{n}\right)\left({1+k_{n}}\right)\cos \theta _{n}-2k_{n}\left({1+k_{n}}\right)\sin ^{2}\theta _{n}\cos \theta _{n}}{\cos \theta _{n+1}\left(1+k_{n}\sin ^{2}\theta _{n}\right)^{2}}}\mathrm {d} \theta _{n}={\frac {\left(1-k_{n}\sin ^{2}\theta _{n}\right)\left({1+k_{n}}\right)\cos \theta _{n}}{\left(1+k_{n}\sin ^{2}\theta _{n}\right){\sqrt {\left(1+k_{n}\sin ^{2}\theta _{n}\right)^{2}-\left(1+k_{n}\right)^{2}\sin ^{2}\theta _{n}}}}}\mathrm {d} \theta _{n}}
On a alors :
d
θ
n
1
−
k
n
2
sin
2
θ
n
=
(
1
+
k
n
sin
2
θ
n
)
d
θ
n
+
1
(
1
−
k
n
sin
2
θ
n
)
(
1
+
k
n
)
=
d
θ
n
+
1
(
1
+
k
n
)
1
−
4
k
n
sin
2
θ
n
(
1
+
k
n
sin
2
θ
n
)
2
=
d
θ
n
+
1
(
1
+
k
n
)
1
−
(
2
k
n
1
+
k
n
)
2
sin
2
θ
n
+
1
{\displaystyle {\frac {\mathrm {d} \theta _{n}}{\sqrt {1-k_{n}^{2}\sin ^{2}\theta _{n}}}}={\frac {\left(1+k_{n}\sin ^{2}\theta _{n}\right)\mathrm {d} \theta _{n+1}}{\left(1-k_{n}\sin ^{2}\theta _{n}\right)\left(1+k_{n}\right)}}={\frac {\mathrm {d} \theta _{n+1}}{\left(1+k_{n}\right){\sqrt {1-{\frac {4k_{n}\sin ^{2}\theta _{n}}{\left(1+k_{n}\sin ^{2}\theta _{n}\right)^{2}}}}}}}={\frac {\mathrm {d} \theta _{n+1}}{\left(1+k_{n}\right){\sqrt {1-\left({\frac {2{\sqrt {k}}_{n}}{1+k_{n}}}\right)^{2}\sin ^{2}\theta _{n+1}}}}}}
Calculons l'amplitude
φ
n
+
1
{\displaystyle \varphi _{n+1}}
φ
0
G
=
φ
{\displaystyle \varphi _{0}^{G}=\varphi }
φ
n
+
1
G
=
arcsin
(
1
+
k
n
)
sin
φ
n
G
1
+
k
n
sin
2
φ
n
G
{\displaystyle \varphi _{n+1}^{G}=\arcsin {\frac {\left(1+k_{n}\right)\sin \varphi _{n}^{G}}{1+k_{n}\sin ^{2}\varphi _{n}^{G}}}}
Calculons l'amplitude
φ
n
G
{\displaystyle \varphi _{n}^{G}}
φ
n
G
=
arcsin
2
sin
φ
n
+
1
G
1
+
k
n
+
1
+
k
n
2
+
2
k
n
cos
(
2
φ
n
+
1
G
)
=
arcsin
(
1
+
k
n
+
1
′
)
sin
φ
n
+
1
G
1
+
1
−
k
n
+
1
2
sin
2
φ
n
+
1
G
{\displaystyle \varphi _{n}^{G}=\arcsin {\frac {2\sin \varphi _{n+1}^{G}}{1+k_{n}+{\sqrt {1+k_{n}^{2}+2k_{n}\cos \left(2\varphi _{n+1}^{G}\right)}}}}=\arcsin {\frac {\left(1+k'_{n+1}\right)\sin \varphi _{n+1}^{G}}{1+{\sqrt {1-k_{n+1}^{2}\sin ^{2}\varphi _{n+1}^{G}}}}}}
Transformation de Landen
[
0
;
π
]
→
[
0
;
π
/
2
]
φ
n
L
↦
φ
n
+
1
L
{\displaystyle {\begin{array}{ccc}[0;\pi ]&\to &[0;\pi /2]\\\varphi _{n}^{L}&\mapsto &\varphi _{n+1}^{L}\end{array}}}
Cliquer pour voir et modifier le graphique. Transformation de Gauss
[
0
;
π
/
2
]
→
[
0
;
π
/
2
]
φ
n
G
↦
φ
n
+
1
G
{\displaystyle {\begin{array}{ccc}[0;\pi /2]&\to &[0;\pi /2]\\\varphi _{n}^{G}&\mapsto &\varphi _{n+1}^{G}\end{array}}}
Cliquer pour voir et modifier le graphique.
φ
n
+
1
L
(
φ
n
L
)
{\displaystyle \varphi _{n+1}^{L}\left(\varphi _{n}^{L}\right)}
et
φ
n
+
1
G
(
φ
n
G
)
{\displaystyle \varphi _{n+1}^{G}\left(\varphi _{n}^{G}\right)}
pour
k
n
∈
[
0
;
1
]
{\displaystyle k_{n}\in [0;1]}
par pas de
0
,
05
{\displaystyle 0{,}05}
. La courbe rouge correspond au cas
k
n
=
0
,
8
{\displaystyle k_{n}=0{,}8}
.
En répétant plusieurs fois de suite la transformation de Landen ou gaussienne, on aura
k
∞
→
1
{\displaystyle k_{\infty }\rightarrow 1}
k
−
∞
→
0
{\displaystyle k_{-\infty }\rightarrow 0}
φ
{\displaystyle \varphi }
k
n
↗
⇒
φ
n
L
/
G
↘
{\displaystyle k_{n}\nearrow \,\Rightarrow \varphi _{n}^{L/G}\searrow }
k
−
n
↘
⇒
φ
−
n
L
/
G
↗
{\displaystyle k_{-n}\searrow \,\Rightarrow \varphi _{-n}^{L/G}\nearrow }
[ 9]
F
(
φ
,
0
)
=
φ
{\displaystyle F\left(\varphi ,0\right)=\varphi }
F
(
φ
,
1
)
=
∫
0
φ
d
θ
1
−
sin
2
θ
=
artanh
sin
φ
=
1
2
ln
1
+
sin
φ
1
−
sin
φ
=
ln
1
+
sin
φ
cos
φ
=
ln
cos
φ
2
+
sin
φ
2
cos
φ
2
−
sin
φ
2
=
ln
1
+
tan
φ
2
1
−
tan
φ
2
=
ln
tan
(
φ
2
+
π
4
)
{\displaystyle F\left(\varphi ,1\right)=\int _{0}^{\varphi }{\frac {\mathrm {d} \theta }{\sqrt {1-\sin ^{2}\theta }}}=\operatorname {artanh} \sin \varphi ={\frac {1}{2}}\ln {\frac {1+\sin \varphi }{1-\sin \varphi }}=\ln {\frac {1+\sin \varphi }{\cos \varphi }}=\ln {\frac {\cos {\frac {\varphi }{2}}+\sin {\frac {\varphi }{2}}}{\cos {\frac {\varphi }{2}}-\sin {\frac {\varphi }{2}}}}=\ln {\frac {1+\tan {\frac {\varphi }{2}}}{1-\tan {\frac {\varphi }{2}}}}=\ln \tan \left({\frac {\varphi }{2}}+{\frac {\pi }{4}}\right)}
Si l'on part d'un module
k
{\displaystyle k}
φ
{\displaystyle \varphi }
Pour la transformation de Landen :
F
(
φ
,
k
)
=
2
1
+
k
F
(
φ
1
L
,
k
1
)
=
2
1
+
k
2
1
+
k
1
F
(
φ
2
L
,
k
2
)
=
2
1
+
k
0
⋯
2
1
+
k
n
−
1
F
(
φ
n
L
,
k
n
)
=
k
1
k
F
(
φ
1
L
,
k
1
)
=
k
1
k
k
2
k
1
F
(
φ
2
L
,
k
2
)
=
k
n
k
0
⋯
k
n
−
1
k
F
(
φ
n
L
,
k
n
)
=
1
+
k
−
1
2
F
(
φ
−
1
L
,
k
−
1
)
=
1
+
k
−
1
2
1
+
k
−
2
2
F
(
φ
−
2
L
,
k
−
2
)
=
1
+
k
−
1
2
⋯
1
+
k
−
n
2
F
(
φ
−
n
L
,
k
−
n
)
=
k
−
1
k
F
(
φ
−
1
L
,
k
−
1
)
=
k
−
1
k
k
−
2
k
−
1
F
(
φ
−
2
L
,
k
−
2
)
=
k
−
n
k
k
−
1
⋯
k
−
n
F
(
φ
−
n
L
,
k
−
n
)
{\displaystyle {\begin{aligned}F\left(\varphi ,k\right)&={2 \over 1+k}F\left(\varphi _{1}^{L},k_{1}\right)&=&{2 \over 1+k}{2 \over 1+k_{1}}F\left(\varphi _{2}^{L},k_{2}\right)&=&{2 \over 1+k_{0}}\cdots {2 \over 1+k_{n-1}}F\left(\varphi _{n}^{L},k_{n}\right)\\&={\frac {k_{1}}{\sqrt {k}}}F\left(\varphi _{1}^{L},k_{1}\right)&=&{\frac {k_{1}}{\sqrt {k}}}{\frac {k_{2}}{\sqrt {k_{1}}}}F\left(\varphi _{2}^{L},k_{2}\right)&=&{\frac {k_{n}{\sqrt {k_{0}\cdots k_{n-1}}}}{k}}F\left(\varphi _{n}^{L},k_{n}\right)\\&={1+k_{-1} \over 2}F\left(\varphi _{-1}^{L},k_{-1}\right)&=&{1+k_{-1} \over 2}{1+k_{-2} \over 2}F\left(\varphi _{-2}^{L},k_{-2}\right)&=&{1+k_{-1} \over 2}\cdots {1+k_{-n} \over 2}F\left(\varphi _{-n}^{L},k_{-n}\right)\\&={\frac {\sqrt {k_{-1}}}{k}}F\left(\varphi _{-1}^{L},k_{-1}\right)&=&{\frac {\sqrt {k_{-1}}}{k}}{\frac {\sqrt {k_{-2}}}{k_{-1}}}F\left(\varphi _{-2}^{L},k_{-2}\right)&=&{\frac {k_{-n}}{k{\sqrt {k_{-1}\cdots k_{-n}}}}}F\left(\varphi _{-n}^{L},k_{-n}\right)\end{aligned}}}
F
(
φ
,
k
)
=
ln
tan
(
φ
∞
L
2
+
π
4
)
∏
n
=
0
∞
2
1
+
k
n
=
ln
tan
(
φ
∞
L
2
+
π
4
)
∏
n
=
0
∞
k
n
k
=
lim
n
→
∞
φ
−
n
L
∏
i
=
1
n
1
+
k
−
i
2
=
lim
n
→
∞
φ
−
n
L
k
−
n
k
∏
i
=
1
n
k
−
i
{\displaystyle F\left(\varphi ,k\right)=\ln \tan \left({\frac {\varphi _{\infty }^{L}}{2}}+{\frac {\pi }{4}}\right)\prod _{n=0}^{\infty }{\frac {2}{1+k_{n}}}=\ln \tan \left({\frac {\varphi _{\infty }^{L}}{2}}+{\frac {\pi }{4}}\right){\frac {\sqrt {\prod _{n=0}^{\infty }k_{n}}}{k}}=\lim \limits _{n\rightarrow \infty }\varphi _{-n}^{L}\prod _{i=1}^{n}{\frac {1+k_{-i}}{2}}=\lim \limits _{n\rightarrow \infty }\varphi _{-n}^{L}{\frac {k_{-n}}{k{\sqrt {\prod _{i=1}^{n}k_{-i}}}}}}
Pour la transformation gaussienne :
F
(
φ
,
k
)
=
1
1
+
k
F
(
φ
1
G
,
k
1
)
=
1
1
+
k
1
1
+
k
1
F
(
φ
2
G
,
k
2
)
=
1
1
+
k
0
⋯
1
1
+
k
n
−
1
F
(
φ
n
G
,
k
n
)
=
k
1
2
k
F
(
φ
1
G
,
k
1
)
=
k
1
2
k
k
2
2
k
1
F
(
φ
2
G
,
k
2
)
=
k
n
k
0
⋯
k
n
−
1
2
n
k
F
(
φ
n
G
,
k
n
)
=
(
1
+
k
−
1
)
F
(
φ
−
1
G
,
k
−
1
)
=
(
1
+
k
−
1
)
(
1
+
k
−
2
)
F
(
φ
−
2
G
,
k
−
2
)
=
(
1
+
k
−
1
)
⋯
(
1
+
k
−
n
)
F
(
φ
−
n
G
,
k
−
n
)
=
2
k
−
1
k
F
(
φ
−
1
G
,
k
−
1
)
=
2
k
−
1
k
2
k
−
2
k
−
1
F
(
φ
−
2
G
,
k
−
2
)
=
2
n
k
−
n
k
k
−
1
⋯
k
−
n
F
(
φ
−
n
G
,
k
−
n
)
{\displaystyle {\begin{aligned}F\left(\varphi ,k\right)&={1 \over 1+k}F\left(\varphi _{1}^{G},k_{1}\right)&=&{1 \over 1+k}{1 \over 1+k_{1}}F\left(\varphi _{2}^{G},k_{2}\right)&=&{1 \over 1+k_{0}}\cdots {1 \over 1+k_{n-1}}F\left(\varphi _{n}^{G},k_{n}\right)\\&={\frac {k_{1}}{2{\sqrt {k}}}}F\left(\varphi _{1}^{G},k_{1}\right)&=&{\frac {k_{1}}{2{\sqrt {k}}}}{\frac {k_{2}}{2{\sqrt {k}}_{1}}}F\left(\varphi _{2}^{G},k_{2}\right)&=&{\frac {k_{n}{\sqrt {k_{0}\cdots k_{n-1}}}}{2^{n}k}}F\left(\varphi _{n}^{G},k_{n}\right)\\&=\left(1+k_{-1}\right)F\left(\varphi _{-1}^{G},k_{-1}\right)&=&\left(1+k_{-1}\right)\left(1+k_{-2}\right)F\left(\varphi _{-2}^{G},k_{-2}\right)&=&\left(1+k_{-1}\right)\cdots \left(1+k_{-n}\right)F\left(\varphi _{-n}^{G},k_{-n}\right)\\&={\frac {2{\sqrt {k_{-1}}}}{k}}F\left(\varphi _{-1}^{G},k_{-1}\right)&=&{\frac {2{\sqrt {k_{-1}}}}{k}}{\frac {2{\sqrt {k_{-2}}}}{k_{-1}}}F\left(\varphi _{-2}^{G},k_{-2}\right)&=&{\frac {2^{n}k_{-n}}{k{\sqrt {k_{-1}\cdots k_{-n}}}}}F\left(\varphi _{-n}^{G},k_{-n}\right)\end{aligned}}}
F
(
φ
,
k
)
=
lim
n
→
∞
ln
tan
(
φ
n
G
2
+
π
4
)
∏
i
=
0
n
1
1
+
k
i
=
lim
n
→
∞
ln
tan
(
φ
n
G
2
+
π
4
)
∏
i
=
0
n
k
n
2
n
k
=
φ
−
∞
G
∏
n
=
1
∞
(
1
+
k
−
n
)
=
φ
−
∞
G
lim
n
→
∞
2
n
k
−
n
k
∏
i
=
1
n
k
−
i
{\displaystyle F\left(\varphi ,k\right)=\lim \limits _{n\rightarrow \infty }\ln \tan \left({\frac {\varphi _{n}^{G}}{2}}+{\frac {\pi }{4}}\right)\prod _{i=0}^{n}{\frac {1}{1+k_{i}}}=\lim \limits _{n\rightarrow \infty }\ln \tan \left({\frac {\varphi _{n}^{G}}{2}}+{\frac {\pi }{4}}\right){\frac {\sqrt {\prod _{i=0}^{n}k_{n}}}{2^{n}k}}=\varphi _{-\infty }^{G}\prod _{n=1}^{\infty }\left(1+k_{-n}\right)=\varphi _{-\infty }^{G}\lim \limits _{n\rightarrow \infty }{\frac {2^{n}k_{-n}}{k{\sqrt {\prod _{i=1}^{n}k_{-i}}}}}}
où
φ
∞
L
{\displaystyle \varphi _{\infty }^{L}}
φ
−
∞
L
{\displaystyle \varphi _{-\infty }^{L}}
φ
∞
G
{\displaystyle \varphi _{\infty }^{G}}
φ
−
∞
G
{\displaystyle \varphi _{-\infty }^{G}}
φ
−
n
L
{\displaystyle \varphi _{-n}^{L}}
n
→
∞
{\displaystyle n\to \infty }
[ A 4]
Les convergences de
k
n
{\displaystyle k_{n}}
k
−
n
{\displaystyle k_{-n}}
−
lg
(
1
−
k
n
)
{\displaystyle -\lg \left({1-k_{n}}\right)}
−
lg
k
−
n
{\displaystyle -\lg k_{-n}}
k
=
0
,
1
⇒
1
−
k
5
<
10
−
14
{\displaystyle k=0{,}1\Rightarrow 1-k_{5}<10^{-14}}
k
=
10
−
100
⇒
1
−
k
11
<
10
−
14
{\displaystyle k=10^{-100}\Rightarrow 1-k_{11}<10^{-14}}
k
=
0
,
9
⇒
k
−
5
<
10
−
14
{\displaystyle k=0{,}9\Rightarrow k_{-5}<10^{-14}}
k
=
1
−
10
−
14
⇒
k
−
8
<
10
−
14
{\displaystyle k=1-10^{-14}\Rightarrow k_{-8}<10^{-14}}
L'intégrale elliptique complète de première espèce est :[ 10]
K
(
k
)
=
F
(
π
2
,
k
)
=
1
+
k
−
1
2
F
(
π
,
k
−
1
)
=
(
1
+
k
−
1
)
K
(
k
−
1
)
=
(
1
+
k
−
1
)
(
1
+
k
−
2
)
K
(
k
−
2
)
=
π
2
∏
n
=
1
∞
(
1
+
k
−
n
)
{\displaystyle K(k)=F\left({\frac {\pi }{2}},k\right)={\frac {1+k_{-1}}{2}}F\left(\pi ,k_{-1}\right)=\left(1+k_{-1}\right)K\left(k_{-1}\right)=(1+k_{-1})(1+k_{-2})K\left(k_{-2}\right)={\frac {\pi }{2}}\prod _{n=1}^{\infty }(1+k_{-n})}
On a[ 11]
K
(
k
n
+
1
)
=
(
1
+
k
n
)
K
(
k
n
)
⇒
K
(
2
k
n
1
+
k
n
)
=
(
1
+
k
n
)
K
(
k
n
)
⇒
K
(
2
k
n
′
1
+
k
n
′
)
=
(
1
+
k
n
′
)
K
(
k
n
′
)
⇒
K
(
k
n
−
1
′
)
=
(
1
+
k
n
′
)
K
(
k
n
′
)
⇒
{\displaystyle K\left(k_{n+1}\right)=\left(1+k_{n}\right)K\left(k_{n}\right)\Rightarrow K\left({\frac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)=\left(1+k_{n}\right)K\left(k_{n}\right)\Rightarrow K\left({\frac {2{\sqrt {k_{n}'}}}{1+k_{n}'}}\right)=\left(1+k_{n}'\right)K\left(k_{n}'\right)\Rightarrow K\left(k_{n-1}'\right)=\left(1+k_{n}'\right)K\left(k_{n}'\right)\Rightarrow }
K
(
k
n
′
)
=
(
1
+
k
n
+
1
′
)
K
(
k
n
+
1
′
)
{\displaystyle K\left(k_{n}'\right)=\left(1+k_{n+1}'\right)K\left(k_{n+1}'\right)}
⇒
2
K
(
k
n
′
)
K
(
k
n
)
=
K
(
k
n
−
1
′
)
K
(
k
n
−
1
)
{\displaystyle \Rightarrow 2{\frac {K\left(k_{n}'\right)}{K\left(k_{n}\right)}}={\frac {K\left(k'_{n-1}\right)}{K\left(k_{n-1}\right)}}}
Transformations de Landen des intégrales elliptiques de deuxième espèce [ modifier | modifier le code ] On pose (avec
a
>
b
{\displaystyle a>b}
[ A 5]
{
F
(
a
,
b
,
φ
)
=
∫
0
φ
d
θ
a
2
cos
2
θ
+
b
2
sin
2
θ
E
(
a
,
b
,
φ
)
=
∫
0
φ
a
2
cos
2
θ
+
b
2
sin
2
θ
d
θ
{\displaystyle {\begin{cases}F\left(a,b,\varphi \right)=\int \limits _{0}^{\varphi }{\frac {\mathrm {d} \theta }{\sqrt {a^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta }}}\\E\left(a,b,\varphi \right)=\int \limits _{0}^{\varphi }{\sqrt {a^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta }}\,\mathrm {d} \theta \end{cases}}}
{
a
n
−
1
=
a
n
+
b
n
2
b
n
−
1
=
a
n
b
n
c
n
−
1
=
a
n
−
b
n
2
{\displaystyle {\begin{cases}a_{n-1}={\frac {a_{n}+b_{n}}{2}}\\b_{n-1}={\sqrt {a_{n}b_{n}}}\\c_{n-1}={\frac {a_{n}-b_{n}}{2}}\end{cases}}}
Le module devient
k
n
=
1
−
(
b
n
a
n
)
2
=
c
n
a
n
{\displaystyle k_{n}={\sqrt {1-\left({\frac {b_{n}}{a_{n}}}\right)^{2}}}={\frac {c_{n}}{a_{n}}}}
k
n
−
1
=
a
n
−
b
n
a
n
+
b
n
{\displaystyle k_{n-1}={\frac {a_{n}-b_{n}}{a_{n}+b_{n}}}}
a
n
2
=
b
n
2
+
c
n
2
{\displaystyle a_{n}^{2}=b_{n}^{2}+c_{n}^{2}}
a
−
1
{\displaystyle a_{-1}}
b
−
1
{\displaystyle b_{-1}}
a
{\displaystyle a}
b
{\displaystyle b}
a
−
i
{\displaystyle a_{-i}}
b
−
i
{\displaystyle b_{-i}}
moyenne arithmético-géométrique de
a
{\displaystyle a}
b
{\displaystyle b}
AGM
(
a
,
b
)
{\displaystyle \operatorname {AGM} (a,b)}
M
(
a
,
b
)
{\displaystyle M(a,b)}
a
−
∞
=
b
−
∞
=
AGM
(
a
,
b
)
{\displaystyle a_{-\infty }=b_{-\infty }=\operatorname {AGM} \left(a,b\right)}
2
1
+
k
n
−
1
d
θ
n
1
−
k
n
2
sin
2
θ
n
=
d
θ
n
−
1
1
−
k
n
−
1
2
sin
2
θ
n
−
1
⇒
2
d
θ
n
a
n
2
cos
2
θ
n
+
b
n
2
sin
2
θ
n
=
d
θ
n
−
1
a
n
−
1
2
cos
2
θ
n
−
1
+
b
n
−
1
2
sin
2
θ
n
−
1
{\displaystyle {\frac {2}{1+k_{n-1}}}{\frac {\mathrm {d} \theta _{n}}{\sqrt {1-k_{n}^{2}\sin ^{2}\theta _{n}}}}={\mathrm {d} \theta _{n-1} \over {\sqrt {1-k_{n-1}^{2}\sin ^{2}\theta _{n-1}}}}\Rightarrow {\frac {2\mathrm {d} \theta _{n}}{\sqrt {a_{n}^{2}\cos ^{2}\theta _{n}+b_{n}^{2}\sin ^{2}\theta _{n}}}}={\frac {\mathrm {d} \theta _{n-1}}{\sqrt {a_{n-1}^{2}\cos ^{2}\theta _{n-1}+b_{n-1}^{2}\sin ^{2}\theta _{n-1}}}}}
et :
cos
(
2
θ
n
L
)
=
−
k
n
−
1
sin
2
θ
n
−
1
L
+
cos
θ
n
−
1
L
1
−
k
n
−
1
2
sin
2
θ
n
−
1
L
{\displaystyle \cos(2\theta _{n}^{L})=-k_{n-1}\sin ^{2}\theta _{n-1}^{L}+\cos \theta _{n-1}^{L}{\sqrt {1-k_{n-1}^{2}\sin ^{2}\theta _{n-1}^{L}}}}
⇒
{
2
cos
2
θ
n
L
=
1
−
k
n
−
1
sin
2
θ
n
−
1
L
+
cos
θ
n
−
1
L
1
−
k
n
−
1
2
sin
2
θ
n
−
1
L
2
sin
2
θ
n
L
=
1
+
k
n
−
1
sin
2
θ
n
−
1
L
−
cos
θ
n
−
1
L
1
−
k
n
−
1
2
sin
2
θ
n
−
1
L
{\displaystyle \Rightarrow {\begin{cases}2\cos ^{2}\theta _{n}^{L}=1-k_{n-1}\sin ^{2}\theta _{n-1}^{L}+\cos \theta _{n-1}^{L}{\sqrt {1-k_{n-1}^{2}\sin ^{2}\theta _{n-1}^{L}}}\\2\sin ^{2}\theta _{n}^{L}=1+k_{n-1}\sin ^{2}\theta _{n-1}^{L}-\cos \theta _{n-1}^{L}{\sqrt {1-k_{n-1}^{2}\sin ^{2}\theta _{n-1}^{L}}}\end{cases}}}
⇒
2
a
n
2
cos
2
θ
n
L
+
2
b
n
2
sin
2
θ
n
L
=
(
a
n
2
+
b
n
2
)
(
cos
2
θ
n
−
1
L
+
sin
2
θ
n
−
1
L
)
−
(
a
n
2
−
b
n
2
)
k
n
−
1
sin
2
θ
n
−
1
L
+
(
a
n
2
−
b
n
2
)
cos
θ
n
−
1
L
1
−
k
n
−
1
2
sin
2
θ
n
−
1
L
=
4
(
a
n
−
1
2
cos
2
θ
n
−
1
L
+
b
n
−
1
2
sin
2
θ
n
−
1
L
)
−
2
b
n
−
1
2
+
4
c
n
−
1
cos
2
θ
n
−
1
L
a
n
−
1
2
cos
2
θ
n
−
1
L
+
b
n
−
1
2
sin
2
θ
n
−
1
L
{\displaystyle {\begin{aligned}\Rightarrow 2a_{n}^{2}\cos ^{2}\theta _{n}^{L}+2b_{n}^{2}\sin ^{2}\theta _{n}^{L}&=\left(a_{n}^{2}+b_{n}^{2}\right)\left(\cos ^{2}\theta _{n-1}^{L}+\sin ^{2}\theta _{n-1}^{L}\right)-\left(a_{n}^{2}-b_{n}^{2}\right)k_{n-1}\sin ^{2}\theta _{n-1}^{L}+\left(a_{n}^{2}-b_{n}^{2}\right)\cos \theta _{n-1}^{L}{\sqrt {1-k_{n-1}^{2}\sin ^{2}\theta _{n-1}^{L}}}\\&=4\left(a_{n-1}^{2}\cos ^{2}\theta _{n-1}^{L}+b_{n-1}^{2}\sin ^{2}\theta _{n-1}^{L}\right)-2b_{n-1}^{2}+4c_{n-1}\cos ^{2}\theta _{n-1}^{L}{\sqrt {a_{n-1}^{2}\cos ^{2}\theta _{n-1}^{L}+b_{n-1}^{2}\sin ^{2}\theta _{n-1}^{L}}}\end{aligned}}}
En intégrant, on obtient :
F
(
a
n
,
b
n
,
φ
n
L
)
=
1
2
F
(
a
n
−
1
,
b
n
−
1
,
φ
n
−
1
L
)
=
1
2
m
F
(
a
n
−
m
,
b
n
−
m
,
φ
n
−
m
L
)
{\displaystyle F\left(a_{n},b_{n},\varphi _{n}^{L}\right)={\frac {1}{2}}F\left(a_{n-1},b_{n-1},\varphi _{n-1}^{L}\right)={\frac {1}{2^{m}}}F\left(a_{n-m},b_{n-m},\varphi _{n-m}^{L}\right)}
E
(
a
n
,
b
n
,
φ
n
L
)
=
E
(
a
n
−
1
,
b
n
−
1
,
φ
n
−
1
L
)
−
b
n
−
1
2
2
E
(
a
n
−
1
,
b
n
−
1
,
φ
n
−
1
L
)
+
c
n
−
1
sin
φ
n
−
1
L
{\displaystyle E\left(a_{n},b_{n},\varphi _{n}^{L}\right)=E\left(a_{n-1},b_{n-1},\varphi _{n-1}^{L}\right)-{\frac {b_{n-1}^{2}}{2}}E\left(a_{n-1},b_{n-1},\varphi _{n-1}^{L}\right)+c_{n-1}\sin \varphi _{n-1}^{L}}
⇒
E
(
φ
n
L
,
k
n
)
=
a
n
−
1
a
n
E
(
φ
n
−
1
L
,
k
n
−
1
)
−
b
n
−
1
2
2
a
n
a
n
−
1
E
(
φ
n
−
1
L
,
k
n
−
1
)
+
c
n
−
1
a
n
sin
φ
n
−
1
L
{\displaystyle \Rightarrow E\left(\varphi _{n}^{L},k_{n}\right)={\frac {a_{n-1}}{a_{n}}}E\left(\varphi _{n-1}^{L},k_{n-1}\right)-{\frac {b_{n-1}^{2}}{2a_{n}a_{n-1}}}E\left(\varphi _{n-1}^{L},k_{n-1}\right)+{\frac {c_{n-1}}{a_{n}}}\sin \varphi _{n-1}^{L}}
⇒
E
(
φ
n
L
,
k
n
)
=
1
+
k
n
′
2
E
(
φ
n
−
1
L
,
k
n
−
1
)
−
k
n
′
1
+
k
n
′
E
(
φ
n
−
1
L
,
k
n
−
1
)
+
1
−
k
n
′
2
sin
φ
n
−
1
L
{\displaystyle \Rightarrow E\left(\varphi _{n}^{L},k_{n}\right)={\frac {1+k_{n}'}{2}}E\left(\varphi _{n-1}^{L},k_{n-1}\right)-{\frac {k_{n}'}{1+k_{n}'}}E\left(\varphi _{n-1}^{L},k_{n-1}\right)+{\frac {1-k_{n}'}{2}}\sin \varphi _{n-1}^{L}}
⇒
E
(
φ
n
L
,
k
n
)
=
1
1
+
k
n
−
1
E
(
φ
n
−
1
L
,
k
n
−
1
)
−
1
−
k
n
−
1
2
F
(
φ
n
−
1
L
,
k
n
−
1
)
+
k
n
−
1
sin
φ
n
−
1
L
1
+
k
n
−
1
{\displaystyle \Rightarrow E\left(\varphi _{n}^{L},k_{n}\right)={\frac {1}{1+k_{n-1}}}E\left(\varphi _{n-1}^{L},k_{n-1}\right)-{\frac {1-k_{n-1}}{2}}F\left(\varphi _{n-1}^{L},k_{n-1}\right)+{\frac {k_{n-1}\sin \varphi _{n-1}^{L}}{1+k_{n-1}}}}
On fera attention comme précédemment si on utilise les notations avec un point-virgule.
E
(
a
,
b
,
φ
)
−
a
2
F
(
a
,
b
,
φ
)
=
E
(
a
−
1
,
b
−
1
,
φ
−
1
L
)
−
a
−
1
2
F
(
a
−
1
,
b
−
1
,
φ
−
1
L
)
+
(
a
−
1
2
−
a
2
2
−
b
−
1
2
2
)
F
(
a
−
1
,
b
−
1
,
φ
−
1
L
)
+
c
−
1
sin
φ
−
1
L
=
E
(
a
−
1
,
b
−
1
,
φ
−
1
L
)
−
a
−
1
2
F
(
a
−
1
,
b
−
1
,
φ
−
1
L
)
−
a
−
1
c
−
1
F
(
a
−
1
,
b
−
1
,
φ
−
1
L
)
+
c
−
1
sin
φ
−
1
L
=
E
(
a
−
1
,
b
−
1
,
φ
−
1
L
)
−
a
−
1
2
F
(
a
−
1
,
b
−
1
,
φ
−
1
L
)
−
2
a
−
1
c
−
1
F
(
a
,
b
,
φ
)
+
c
−
1
sin
φ
−
1
L
=
E
(
a
−
2
,
b
−
2
,
φ
−
2
L
)
−
a
−
2
2
F
(
a
−
2
,
b
−
2
,
φ
−
2
L
)
−
2
a
−
1
c
−
1
F
(
a
,
b
,
φ
)
−
4
a
−
2
c
−
2
F
(
a
,
b
,
φ
)
+
c
−
1
sin
φ
−
1
L
+
c
−
2
sin
φ
−
2
L
=
AGM
(
a
,
b
)
φ
−
∞
L
−
AGM
(
a
,
b
)
φ
−
∞
L
−
∑
n
=
1
∞
2
n
a
−
n
c
−
n
F
(
a
,
b
,
φ
)
+
∑
n
=
1
∞
c
−
n
sin
φ
−
n
L
=
−
∑
n
=
1
∞
2
n
a
−
n
c
−
n
F
(
a
,
b
,
φ
)
+
∑
n
=
1
∞
c
−
n
sin
φ
−
n
L
{\displaystyle {\begin{aligned}E\left(a,b,\varphi \right)-a^{2}F\left(a,b,\varphi \right)&=E\left(a_{-1},b_{-1},\varphi _{-1}^{L}\right)-a_{-1}^{2}F\left(a_{-1},b_{-1},\varphi _{-1}^{L}\right)+\left(a_{-1}^{2}-{\frac {a^{2}}{2}}-{\frac {b_{-1}^{2}}{2}}\right)F\left(a_{-1},b_{-1},\varphi _{-1}^{L}\right)+c_{-1}\sin \varphi _{-1}^{L}\\&=E\left(a_{-1},b_{-1},\varphi _{-1}^{L}\right)-a_{-1}^{2}F\left(a_{-1},b_{-1},\varphi _{-1}^{L}\right)-a_{-1}c_{-1}F\left(a_{-1},b_{-1},\varphi _{-1}^{L}\right)+c_{-1}\sin \varphi _{-1}^{L}\\&=E\left(a_{-1},b_{-1},\varphi _{-1}^{L}\right)-a_{-1}^{2}F\left(a_{-1},b_{-1},\varphi _{-1}^{L}\right)-2a_{-1}c_{-1}F\left(a,b,\varphi \right)+c_{-1}\sin \varphi _{-1}^{L}\\&=E\left(a_{-2},b_{-2},\varphi _{-2}^{L}\right)-a_{-2}^{2}F\left(a_{-2},b_{-2},\varphi _{-2}^{L}\right)-2a_{-1}c_{-1}F\left(a,b,\varphi \right)-4a_{-2}c_{-2}F\left(a,b,\varphi \right)+c_{-1}\sin \varphi _{-1}^{L}+c_{-2}\sin \varphi _{-2}^{L}\\&=\operatorname {AGM} \left(a,b\right)\varphi _{-\infty }^{L}-\operatorname {AGM} \left(a,b\right)\varphi _{-\infty }^{L}-\sum \limits _{n=1}^{\infty }2^{n}a_{-n}c_{-n}F\left(a,b,\varphi \right)+\sum \limits _{n=1}^{\infty }c_{-n}\sin \varphi _{-n}^{L}\\&=-\sum \limits _{n=1}^{\infty }2^{n}a_{-n}c_{-n}F\left(a,b,\varphi \right)+\sum \limits _{n=1}^{\infty }c_{-n}\sin \varphi _{-n}^{L}\end{aligned}}}
E
(
a
,
b
,
φ
)
=
[
a
2
−
∑
n
=
1
∞
2
n
a
−
n
c
−
n
]
F
(
a
,
b
,
φ
)
+
∑
n
=
1
∞
c
−
n
sin
φ
−
n
L
{\displaystyle E\left(a,b,\varphi \right)=\left[a^{2}-\sum \limits _{n=1}^{\infty }2^{n}a_{-n}c_{-n}\right]F\left(a,b,\varphi \right)+\sum \limits _{n=1}^{\infty }c_{-n}\sin \varphi _{-n}^{L}}
E
(
φ
,
k
)
=
[
1
−
∑
n
=
1
∞
2
n
a
−
n
c
−
n
a
2
]
F
(
φ
,
k
)
+
∑
n
=
1
∞
c
−
n
a
sin
φ
−
n
L
=
[
1
−
2
a
−
1
c
−
1
a
2
−
2
a
−
1
c
−
1
a
2
2
a
−
2
c
−
2
a
−
1
c
−
1
−
2
a
−
1
c
−
1
a
2
2
a
−
2
c
−
2
a
−
1
c
−
1
2
a
−
3
c
−
3
a
−
2
c
−
2
−
⋯
]
F
(
φ
,
k
)
+
c
−
1
a
sin
φ
−
1
L
+
a
−
1
a
c
−
2
a
−
1
sin
φ
−
2
L
+
a
−
1
a
a
−
2
a
−
1
c
−
3
a
−
2
sin
φ
−
3
L
+
⋯
=
[
1
−
k
2
2
(
1
+
k
−
1
2
+
k
−
1
k
−
2
4
+
k
−
1
k
−
2
k
−
3
8
+
⋯
)
]
F
(
φ
,
k
)
+
k
−
1
1
+
k
−
1
sin
φ
−
1
L
+
1
1
+
k
−
1
k
−
2
1
+
k
−
2
sin
φ
−
2
L
+
1
1
+
k
−
1
1
1
+
k
−
2
k
−
3
1
+
k
−
3
sin
φ
−
3
L
+
⋯
=
[
1
−
k
2
2
(
∑
n
=
0
∞
∏
i
=
1
n
k
−
i
2
n
)
]
F
(
φ
,
k
)
+
∑
n
=
1
∞
k
−
n
∏
i
=
1
n
(
1
+
k
−
i
)
sin
φ
−
n
L
=
[
1
−
k
2
2
(
1
+
k
−
1
2
+
k
−
1
k
−
2
4
+
k
−
1
k
−
2
k
−
3
8
+
⋯
)
]
F
(
φ
,
k
)
+
k
−
1
k
2
k
−
1
sin
φ
−
1
L
+
k
−
2
k
2
k
−
1
k
−
1
2
k
−
2
sin
φ
−
2
L
+
k
−
3
k
2
k
−
1
k
−
1
2
k
−
2
k
−
2
2
k
−
3
sin
φ
−
3
L
+
⋯
=
[
1
−
k
2
2
(
1
+
k
−
1
2
+
k
−
1
k
−
2
4
+
k
−
1
k
−
2
k
−
3
8
+
⋯
)
]
F
(
φ
,
k
)
+
k
[
k
−
1
2
sin
φ
−
1
L
+
k
−
1
k
−
2
4
sin
φ
−
2
L
+
k
−
1
k
−
2
k
−
3
8
sin
φ
−
3
L
+
⋯
]
=
[
1
−
k
2
2
(
∑
n
=
0
∞
∏
i
=
1
n
k
−
i
2
n
)
]
F
(
φ
,
k
)
+
k
∑
n
=
1
∞
∏
i
=
1
n
k
−
i
2
n
sin
φ
−
n
L
{\displaystyle {\begin{aligned}E\left(\varphi ,k\right)&=\left[1-\sum \limits _{n=1}^{\infty }{\frac {2^{n}a_{-n}c_{-n}}{a^{2}}}\right]F\left(\varphi ,k\right)+\sum \limits _{n=1}^{\infty }{\frac {c_{-n}}{a}}\sin \varphi _{-n}^{L}\\&=\left[1-{\frac {2a_{-1}c_{-1}}{a^{2}}}-{\frac {2a_{-1}c_{-1}}{a^{2}}}{\frac {2a_{-2}c_{-2}}{a_{-1}c_{-1}}}-{\frac {2a_{-1}c_{-1}}{a^{2}}}{\frac {2a_{-2}c_{-2}}{a_{-1}c_{-1}}}{\frac {2a_{-3}c_{-3}}{a_{-2}c_{-2}}}-\cdots \right]F\left(\varphi ,k\right)+\scriptstyle {\frac {c_{-1}}{a}}\displaystyle \sin \varphi _{-1}^{L}+\scriptstyle {\frac {a_{-1}}{a}}{\frac {c_{-2}}{a_{-1}}}\displaystyle \sin \varphi _{-2}^{L}+\scriptstyle {\frac {a_{-1}}{a}}{\frac {a_{-2}}{a_{-1}}}{\frac {c_{-3}}{a_{-2}}}\displaystyle \sin \varphi _{-3}^{L}+\cdots \\&=\left[1-{\frac {k^{2}}{2}}\left(1+{\frac {k_{-1}}{2}}+{\frac {k_{-1}k_{-2}}{4}}+{\frac {k_{-1}k_{-2}k_{-3}}{8}}+\cdots \right)\right]F\left(\varphi ,k\right)+\scriptstyle {\frac {k_{-1}}{1+k_{-1}}}\displaystyle \sin \varphi _{-1}^{L}+\scriptstyle {\frac {1}{1+k_{-1}}}{\frac {k_{-2}}{1+k_{-2}}}\displaystyle \sin \varphi _{-2}^{L}+\scriptstyle {\frac {1}{1+k_{-1}}}{\frac {1}{1+k_{-2}}}{\frac {k_{-3}}{1+k_{-3}}}\displaystyle \sin \varphi _{-3}^{L}+\cdots \\&=\left[1-{\frac {k^{2}}{2}}\left(\sum \limits _{n=0}^{\infty }\prod \limits _{i=1}^{n}{\frac {k_{-i}}{2^{n}}}\right)\right]F\left(\varphi ,k\right)+\sum \limits _{n=1}^{\infty }{\frac {k_{-n}}{\prod \limits _{i=1}^{n}\left(1+k_{-i}\right)}}\sin \varphi _{-n}^{L}\\&=\left[1-{\frac {k^{2}}{2}}\left(1+{\frac {k_{-1}}{2}}+{\frac {k_{-1}k_{-2}}{4}}+{\frac {k_{-1}k_{-2}k_{-3}}{8}}+\cdots \right)\right]F\left(\varphi ,k\right)+\scriptstyle k_{-1}{\frac {k}{2{\sqrt {k_{-1}}}}}\displaystyle \sin \varphi _{-1}^{L}+\scriptstyle k_{-2}{\frac {k}{2{\sqrt {k_{-1}}}}}{\frac {k_{-1}}{2{\sqrt {k_{-2}}}}}\displaystyle \sin \varphi _{-2}^{L}+\scriptstyle k_{-3}{\frac {k}{2{\sqrt {k_{-1}}}}}{\frac {k_{-1}}{2{\sqrt {k_{-2}}}}}{\frac {k_{-2}}{2{\sqrt {k_{-3}}}}}\displaystyle \sin \varphi _{-3}^{L}+\cdots \\&=\left[1-{\frac {k^{2}}{2}}\left(1+{\frac {k_{-1}}{2}}+{\frac {k_{-1}k_{-2}}{4}}+{\frac {k_{-1}k_{-2}k_{-3}}{8}}+\cdots \right)\right]F\left(\varphi ,k\right)+k\left[\scriptstyle {\frac {\sqrt {k_{-1}}}{2}}\displaystyle \sin \varphi _{-1}^{L}+\scriptstyle {\frac {\sqrt {k_{-1}k_{-2}}}{4}}\displaystyle \sin \varphi _{-2}^{L}+\scriptstyle {\frac {\sqrt {k_{-1}k_{-2}k_{-3}}}{8}}\displaystyle \sin \varphi _{-3}^{L}+\cdots \right]\\&=\left[1-{\frac {k^{2}}{2}}\left(\sum \limits _{n=0}^{\infty }\prod \limits _{i=1}^{n}{\frac {k_{-i}}{2^{n}}}\right)\right]F\left(\varphi ,k\right)+k\sum \limits _{n=1}^{\infty }{\frac {\sqrt {\prod \limits _{i=1}^{n}k_{-i}}}{2^{n}}}\sin \varphi _{-n}^{L}\end{aligned}}}
L'intégrale elliptique complète de deuxième espèce est :[ A 6]
E
(
k
)
=
[
1
−
k
2
2
(
∑
n
=
0
∞
∏
i
=
1
n
k
−
i
2
n
)
]
K
(
k
)
{\displaystyle E\left(k\right)=\left[1-{\frac {k^{2}}{2}}\left(\sum \limits _{n=0}^{\infty }\prod \limits _{i=1}^{n}{\frac {k_{-i}}{2^{n}}}\right)\right]K\left(k\right)}
On remarque une formule de Gauss :
F
(
a
,
b
,
π
/
2
)
=
1
2
F
(
a
−
1
,
b
−
1
,
π
)
=
F
(
a
−
1
,
b
−
1
,
π
/
2
)
=
F
(
a
+
b
2
,
a
b
,
π
/
2
)
{\displaystyle F\left(a,b,\pi /2\right)={\frac {1}{2}}F\left(a_{-1},b_{-1},\pi \right)=F\left(a_{-1},b_{-1},\pi /2\right)=F\left({\frac {a+b}{2}},{\sqrt {ab}},\pi /2\right)}
Donc, on a :
F
(
a
,
b
,
π
/
2
)
=
π
2
AGM
(
a
,
b
)
=
1
a
K
(
1
−
(
b
a
)
2
)
=
2
a
+
b
K
(
a
−
b
a
+
b
)
⇔
AGM
(
a
,
b
)
=
π
a
2
K
(
1
−
(
b
a
)
2
)
=
π
(
a
+
b
)
4
K
(
a
−
b
a
+
b
)
{\displaystyle F\left(a,b,\pi /2\right)={\frac {\pi }{2\operatorname {AGM} (a,b)}}={\frac {1}{a}}K\left({\sqrt {1-\left({\frac {b}{a}}\right)^{2}}}\right)={\frac {2}{a+b}}K\left({\frac {a-b}{a+b}}\right)\Leftrightarrow \operatorname {AGM} (a,b)={\frac {\pi a}{2K\left({\sqrt {1-\left({\frac {b}{a}}\right)^{2}}}\right)}}={\frac {\pi \left(a+b\right)}{4K\left({\frac {a-b}{a+b}}\right)}}}
En opérant
a
→
1
{\displaystyle a\rightarrow 1}
b
→
k
{\displaystyle b\rightarrow k}
K
(
k
)
=
π
2
AGM
(
1
,
1
−
k
2
)
=
π
2
AGM
(
1
+
k
,
1
−
k
)
{\displaystyle K(k)={\frac {\pi }{2\operatorname {AGM} (1,{\sqrt {1-k^{2}}})}}={\frac {\pi }{2\operatorname {AGM} (1+k,1-k)}}}
Transformations de Landen des intégrales elliptiques de troisième espèce [ modifier | modifier le code ] On a aussi une transformation de Landen des intégrales elliptiques de troisième espèce .
Transformation de Landen des fonctions elliptiques jacobiennes [ modifier | modifier le code ] Le module elliptique initial est
0
<
k
<
1
{\displaystyle 0<k<1}
Démonstration de la transformation croissante [ modifier | modifier le code ]
sn
(
u
n
,
k
n
)
=
2
1
+
k
n
sn
(
u
n
+
1
,
k
n
+
1
)
cn
(
u
n
+
1
,
k
n
+
1
)
1
−
(
2
k
n
1
+
k
n
)
2
sn
2
(
u
n
+
1
,
k
n
+
1
)
=
2
1
+
k
n
sn
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
cn
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
dn
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
{\displaystyle \operatorname {sn} \left(u_{n},k_{n}\right)={\frac {{\frac {2}{1+k_{n}}}\operatorname {sn} \left(u_{n+1},k_{n+1}\right)\operatorname {cn} \left(u_{n+1},k_{n+1}\right)}{\sqrt {1-\left({\frac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)^{2}\operatorname {sn} ^{2}\left(u_{n+1},k_{n+1}\right)}}}={\frac {{\frac {2}{1+k_{n}}}\operatorname {sn} \left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)\operatorname {cn} \left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)}{\operatorname {dn} \left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)}}}
cn
(
u
n
,
k
n
)
=
1
−
sn
2
(
u
n
,
k
n
)
=
1
−
2
1
+
k
n
sn
2
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
dn
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
=
dn
2
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
−
1
−
k
n
1
+
k
n
2
k
n
1
+
k
n
dn
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
{\displaystyle \operatorname {cn} \left(u_{n},k_{n}\right)={\sqrt {1-\operatorname {sn} ^{2}\left(u_{n},k_{n}\right)}}={\frac {1-{\tfrac {2}{1+k_{n}}}\operatorname {sn} ^{2}\left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)}{\operatorname {dn} \left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)}}={\frac {\operatorname {dn} ^{2}\left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)-{\tfrac {1-k_{n}}{1+k_{n}}}}{{\tfrac {2k_{n}}{1+k_{n}}}\operatorname {dn} \left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)}}}
dn
(
u
n
,
k
n
)
=
1
−
k
n
2
sn
2
(
u
n
,
k
n
)
=
1
−
2
k
n
1
+
k
n
sn
2
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
dn
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
=
dn
2
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
+
1
−
k
n
1
+
k
n
2
1
+
k
n
dn
(
1
+
k
n
2
u
n
,
2
k
n
1
+
k
n
)
{\displaystyle \operatorname {dn} \left(u_{n},k_{n}\right)={\sqrt {1-k_{n}^{2}\operatorname {sn} ^{2}\left(u_{n},k_{n}\right)}}={\frac {1-{\tfrac {2k_{n}}{1+k_{n}}}\operatorname {sn} ^{2}\left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)}{\operatorname {dn} \left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)}}={\frac {\operatorname {dn} ^{2}\left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)+{\tfrac {1-k_{n}}{1+k_{n}}}}{{\tfrac {2}{1+k_{n}}}\operatorname {dn} \left({\tfrac {1+k_{n}}{2}}u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)}}}
Démonstration de la transformation décroissante [ modifier | modifier le code ] En opérant les transformations
u
n
→
u
n
1
+
k
n
{\displaystyle u_{n}\rightarrow {\frac {u_{n}}{1+k_{n}}}}
k
n
→
1
−
1
−
k
n
2
1
+
1
−
k
n
2
{\displaystyle k_{n}\rightarrow {\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}}
sn
(
(
1
+
k
n
)
u
n
,
2
k
n
1
+
k
n
)
=
sn
(
u
n
+
1
,
k
n
+
1
)
=
(
1
+
k
n
)
sn
(
u
n
,
k
n
)
1
+
k
n
sn
2
(
u
n
,
k
n
)
{\displaystyle \operatorname {sn} \left((1+k_{n})u_{n},{\tfrac {2{\sqrt {k_{n}}}}{1+k_{n}}}\right)=\operatorname {sn} \left(u_{n+1},k_{n+1}\right)={\frac {\left(1+k_{n}\right)\operatorname {sn} \left(u_{n},k_{n}\right)}{1+k_{n}\operatorname {sn} ^{2}\left(u_{n},k_{n}\right)}}}
sn
(
u
n
,
k
n
)
=
2
1
+
1
−
k
n
2
sn
(
1
+
1
−
k
n
2
2
u
n
,
1
−
1
−
k
n
2
1
+
1
−
k
n
2
)
1
+
1
−
1
−
k
n
2
1
+
1
−
k
n
2
sn
2
(
1
+
1
−
k
n
2
2
u
n
,
1
−
1
−
k
n
2
1
+
1
−
k
n
2
)
{\displaystyle \operatorname {sn} \left(u_{n},k_{n}\right)={\frac {{\tfrac {2}{1+{\sqrt {1-k_{n}^{2}}}}}\operatorname {sn} \left({\tfrac {1+{\sqrt {1-k_{n}^{2}}}}{2}}u_{n},{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\right)}{1+{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\operatorname {sn} ^{2}\left({\tfrac {1+{\sqrt {1-k_{n}^{2}}}}{2}}u_{n},{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\right)}}}
cn
(
u
n
,
k
n
)
=
1
−
sn
2
(
u
n
,
k
n
)
=
cn
(
1
+
1
−
k
n
2
2
u
n
,
1
−
1
−
k
n
2
1
+
1
−
k
n
2
)
dn
(
1
+
1
−
k
n
2
2
u
n
,
1
−
1
−
k
n
2
1
+
1
−
k
n
2
)
1
+
1
−
1
−
k
n
2
1
+
1
−
k
n
2
sn
2
(
1
+
1
−
k
n
2
2
u
n
,
1
−
1
−
k
n
2
1
+
1
−
k
n
2
)
{\displaystyle \operatorname {cn} \left(u_{n},k_{n}\right)={\sqrt {1-\operatorname {sn} ^{2}\left(u_{n},k_{n}\right)}}={\frac {\operatorname {cn} \left({\tfrac {1+{\sqrt {1-k_{n}^{2}}}}{2}}u_{n},{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\right)\operatorname {dn} \left({\tfrac {1+{\sqrt {1-k_{n}^{2}}}}{2}}u_{n},{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\right)}{1+{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\operatorname {sn} ^{2}\left({\tfrac {1+{\sqrt {1-k_{n}^{2}}}}{2}}u_{n},{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\right)}}}
dn
(
u
n
,
k
n
)
=
1
−
k
n
2
sn
2
(
u
n
,
k
n
)
=
1
−
1
−
1
−
k
n
2
1
+
1
−
k
n
2
sn
2
(
1
+
1
−
k
n
2
2
u
n
,
1
−
1
−
k
n
2
1
+
1
−
k
n
2
)
1
+
1
−
1
−
k
n
2
1
+
1
−
k
n
2
sn
2
(
1
+
1
−
k
n
2
2
u
n
,
1
−
1
−
k
n
2
1
+
1
−
k
n
2
)
=
dn
2
(
1
+
1
−
k
n
2
2
u
n
,
1
−
1
−
k
n
2
1
+
1
−
k
n
2
)
−
2
1
−
k
n
2
1
+
1
−
k
n
2
2
1
+
1
−
k
n
2
−
dn
2
(
1
+
1
−
k
n
2
2
u
n
,
1
−
1
−
k
n
2
1
+
1
−
k
n
2
)
{\displaystyle \operatorname {dn} \left(u_{n},k_{n}\right)={\sqrt {1-k_{n}^{2}\operatorname {sn} ^{2}\left(u_{n},k_{n}\right)}}={\frac {1-{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\operatorname {sn} ^{2}\left({\tfrac {1+{\sqrt {1-k_{n}^{2}}}}{2}}u_{n},{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\right)}{1+{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\operatorname {sn} ^{2}\left({\tfrac {1+{\sqrt {1-k_{n}^{2}}}}{2}}u_{n},{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\right)}}={\frac {\operatorname {dn} ^{2}\left({\tfrac {1+{\sqrt {1-k_{n}^{2}}}}{2}}u_{n},{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\right)-{\tfrac {2{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}}{{\tfrac {2}{1+{\sqrt {1-k_{n}^{2}}}}}-\operatorname {dn} ^{2}\left({\tfrac {1+{\sqrt {1-k_{n}^{2}}}}{2}}u_{n},{\tfrac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}\right)}}}
La transformation de Landen croissante et la transformation de Landen décroissante sont alternées par la transformation imaginaire.
sn
(
i
u
,
1
−
k
2
)
=
i
sc
(
u
,
k
)
=
i
sn
(
u
,
k
)
cn
(
u
,
k
)
{\displaystyle \operatorname {sn} \left(iu,{\sqrt {1-k^{2}}}\right)=i\operatorname {sc} \left(u,k\right)={\frac {i\operatorname {sn} \left(u,k\right)}{\operatorname {cn} \left(u,k\right)}}}
[ A 7]
En utilisant la transformation de Landen croissante, on a :
i
sn
(
u
,
k
)
cn
(
u
,
k
)
=
2
i
1
+
k
sn
(
1
+
k
2
u
,
2
k
1
+
k
)
cn
(
1
+
k
2
u
,
2
k
1
+
k
)
dn
(
1
+
k
2
u
,
2
k
1
+
k
)
dn
2
(
1
+
k
2
u
,
2
k
1
+
k
)
−
1
−
k
1
+
k
2
k
1
+
k
dn
(
1
+
k
2
u
,
2
k
1
+
k
)
=
4
k
i
(
1
+
k
)
2
sn
(
1
+
k
2
u
,
2
k
1
+
k
)
cn
(
1
+
k
2
u
,
2
k
1
+
k
)
dn
2
(
1
+
k
2
u
,
2
k
1
+
k
)
−
1
−
k
1
+
k
{\displaystyle {\frac {i\operatorname {sn} \left(u,k\right)}{\operatorname {cn} \left(u,k\right)}}={\frac {\frac {{\tfrac {2i}{1+k}}\operatorname {sn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)\operatorname {cn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)}{\operatorname {dn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)}}{\frac {\operatorname {dn} ^{2}\left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)-{\tfrac {1-k}{1+k}}}{{\tfrac {2k}{1+k}}\operatorname {dn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)}}}={\frac {{\tfrac {4ki}{(1+k)^{2}}}\operatorname {sn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)\operatorname {cn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)}{\operatorname {dn} ^{2}\left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)-{\tfrac {1-k}{1+k}}}}}
En utilisant la transformation imaginaire, on a :[ A 7]
sn
(
i
u
,
1
−
k
2
)
=
4
k
(
1
+
k
)
2
sc
(
1
+
k
2
i
u
,
1
−
k
1
+
k
)
nc
(
1
+
k
2
i
u
,
1
−
k
1
+
k
)
dc
2
(
1
+
k
2
i
u
,
1
−
k
1
+
k
)
−
1
−
k
1
+
k
=
4
k
(
1
+
k
)
2
sn
(
1
+
k
2
i
u
,
1
−
k
1
+
k
)
dn
2
(
1
+
k
2
i
u
,
1
−
k
1
+
k
)
−
1
−
k
1
+
k
cn
2
(
1
+
k
2
i
u
,
1
−
k
1
+
k
)
=
2
1
+
k
sn
(
1
+
k
2
i
u
,
1
−
k
1
+
k
)
1
+
1
−
k
1
+
k
sn
2
(
1
+
k
2
i
u
,
1
−
k
1
+
k
)
{\displaystyle \operatorname {sn} \left(iu,{\sqrt {1-k^{2}}}\right)={\frac {{\tfrac {4k}{(1+k)^{2}}}\operatorname {sc} \left({\tfrac {1+k}{2}}iu,{\tfrac {1-k}{1+k}}\right)\operatorname {nc} \left({\tfrac {1+k}{2}}iu,{\tfrac {1-k}{1+k}}\right)}{\operatorname {dc} ^{2}\left({\tfrac {1+k}{2}}iu,{\tfrac {1-k}{1+k}}\right)-{\tfrac {1-k}{1+k}}}}={\frac {{\tfrac {4k}{(1+k)^{2}}}\operatorname {sn} \left({\tfrac {1+k}{2}}iu,{\tfrac {1-k}{1+k}}\right)}{\operatorname {dn} ^{2}\left({\tfrac {1+k}{2}}iu,{\tfrac {1-k}{1+k}}\right)-{\tfrac {1-k}{1+k}}\operatorname {cn} ^{2}\left({\tfrac {1+k}{2}}iu,{\tfrac {1-k}{1+k}}\right)}}={\frac {{\tfrac {2}{1+k}}\operatorname {sn} \left({\tfrac {1+k}{2}}iu,{\tfrac {1-k}{1+k}}\right)}{1+{\tfrac {1-k}{1+k}}\operatorname {sn} ^{2}\left({\tfrac {1+k}{2}}iu,{\tfrac {1-k}{1+k}}\right)}}}
En opérant
i
u
→
u
{\displaystyle \mathrm {i} u\rightarrow u}
1
−
k
2
→
k
{\displaystyle {\sqrt {1-k^{2}}}\rightarrow k}
sn
(
u
,
k
)
=
2
1
+
1
−
k
2
sn
(
1
+
1
−
k
2
2
u
,
1
−
1
−
k
2
1
+
1
−
k
2
)
1
+
1
−
1
−
k
2
1
+
1
−
k
2
sn
2
(
1
+
1
−
k
2
2
u
,
1
−
1
−
k
2
1
+
1
−
k
2
)
{\displaystyle {\begin{aligned}\operatorname {sn} \left(u,k\right)&={\frac {{\tfrac {2}{1+{\sqrt {1-k^{2}}}}}\operatorname {sn} \left({\tfrac {1+{\sqrt {1-k^{2}}}}{2}}u,{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)}{1+{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\operatorname {sn} ^{2}\left({\tfrac {1+{\sqrt {1-k^{2}}}}{2}}u,{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)}}\end{aligned}}}
Il s'agit d'une transformation de Landen décroissante.
Les transformations de modules suivantes peuvent être effectuées à l'aide des Amplitudinis Sine et des Amplitudinis Delta [ 12]
K
(
k
)
≡
3
sn
[
1
3
K
(
k
)
,
k
]
2
−
sn
[
1
3
K
(
k
)
,
k
]
K
{
k
3
sn
[
1
3
K
(
k
)
,
k
]
4
}
{\displaystyle K(k)\equiv {\frac {3\operatorname {sn} \left[{\tfrac {1}{3}}K(k),k\right]}{2-\operatorname {sn} \left[{\tfrac {1}{3}}K(k),k\right]}}K\left\{k^{3}\operatorname {sn} \left[{\tfrac {1}{3}}K(k),k\right]^{4}\right\}}
K
(
k
)
≡
5
1
+
2
dn
[
2
5
K
(
k
)
,
k
]
+
2
dn
[
4
5
K
(
k
)
,
k
]
K
{
k
5
sn
[
1
5
K
(
k
)
,
k
]
4
sn
[
3
5
K
(
k
)
,
k
]
4
}
{\displaystyle K(k)\equiv {\frac {5}{1+2\operatorname {dn} \left[{\tfrac {2}{5}}K(k),k\right]+2\operatorname {dn} \left[{\tfrac {4}{5}}K(k),k\right]}}K\left\{k^{5}\operatorname {sn} \left[{\tfrac {1}{5}}K(k),k\right]^{4}\operatorname {sn} \left[{\tfrac {3}{5}}K(k),k\right]^{4}\right\}}
K
(
k
)
≡
7
1
+
2
dn
[
2
7
K
(
k
)
,
k
]
+
2
dn
[
4
7
K
(
k
)
,
k
]
+
2
dn
[
6
7
K
(
k
)
,
k
]
K
{
k
7
sn
[
1
7
K
(
k
)
,
k
]
4
sn
[
3
7
K
(
k
)
,
k
]
4
sn
[
5
7
K
(
k
)
,
k
]
4
}
{\displaystyle K(k)\equiv {\frac {7}{1+2\operatorname {dn} \left[{\tfrac {2}{7}}K(k),k\right]+2\operatorname {dn} \left[{\tfrac {4}{7}}K(k),k\right]+2\operatorname {dn} \left[{\tfrac {6}{7}}K(k),k\right]}}K\left\{k^{7}\operatorname {sn} \left[{\tfrac {1}{7}}K(k),k\right]^{4}\operatorname {sn} \left[{\tfrac {3}{7}}K(k),k\right]^{4}\operatorname {sn} \left[{\tfrac {5}{7}}K(k),k\right]^{4}\right\}}
Ici, la fonction sinus de Jacobi
sn
[
1
3
K
(
k
)
,
k
]
{\displaystyle \operatorname {sn} \left[{\tfrac {1}{3}}K(k),k\right]}
k
2
x
4
−
2
k
2
x
3
+
2
x
−
1
=
0
{\displaystyle k^{2}x^{4}-2k^{2}x^{3}+2x-1=0}
Globalement, la formule suivante s'applique à toutes les valeurs
n
∈
N
{\displaystyle n\in \mathbb {N} }
0
⩽
k
⩽
1
{\displaystyle 0\leqslant k\leqslant 1}
K
(
k
)
≡
n
∑
a
=
1
n
dn
[
2
a
n
K
(
k
)
,
k
]
K
{
k
n
∏
a
=
1
n
sn
[
2
a
−
1
n
K
(
k
)
,
k
]
2
}
{\displaystyle K(k)\equiv {\frac {n}{\sum \limits _{a=1}^{n}\operatorname {dn} \left[{\frac {2a}{n}}K(k),k\right]}}K\left\{k^{n}\prod _{a=1}^{n}\operatorname {sn} \left[{\frac {2a-1}{n}}K(k),k\right]^{2}\right\}}
Transformations de Landen des intégrales elliptiques de première espèce
Transformation croissante
Transformation décroissante
Landen
F
(
φ
,
k
)
=
2
1
+
k
F
(
arcsin
1
+
k
sin
2
φ
−
cos
φ
1
−
k
2
sin
2
φ
2
,
2
k
1
+
k
)
{\displaystyle \textstyle F\left(\varphi ,k\right)={\frac {2}{1+k}}F\left(\arcsin {\sqrt {\frac {1+k\sin ^{2}\varphi -\cos \varphi {\sqrt {1-k^{2}\sin ^{2}\varphi }}}{2}}},{\frac {2{\sqrt {k}}}{1+k}}\right)}
F
(
φ
,
k
)
=
1
1
+
1
−
k
2
F
(
arccos
1
−
(
1
+
1
−
k
2
)
sin
2
φ
1
−
k
2
sin
2
φ
,
1
−
1
−
k
2
1
+
1
−
k
2
)
{\displaystyle \textstyle F\left(\varphi ,k\right)={\frac {1}{1+{\sqrt {1-k^{2}}}}}F\left(\arccos {\frac {1-\left(1+{\sqrt {1-k^{2}}}\right)\sin ^{2}\varphi }{\sqrt {1-k^{2}\sin ^{2}\varphi }}},{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)}
Gauss
F
(
φ
,
k
)
=
1
1
+
k
F
(
arcsin
(
1
+
k
)
sin
φ
1
+
k
sin
2
φ
,
2
k
1
+
k
)
{\displaystyle \textstyle F\left(\varphi ,k\right)={\frac {1}{1+k}}F\left(\arcsin {\frac {(1+k)\sin \varphi }{1+k\sin ^{2}\varphi }},{\frac {2{\sqrt {k}}}{1+k}}\right)}
F
(
φ
,
k
)
=
2
1
+
1
−
k
2
F
(
arcsin
(
1
+
1
−
k
2
)
sin
φ
1
+
1
−
k
2
sin
2
φ
,
1
−
1
−
k
2
1
+
1
−
k
2
)
{\displaystyle \textstyle F\left(\varphi ,k\right)={\frac {2}{1+{\sqrt {1-k^{2}}}}}F\left(\arcsin {\frac {\left(1+{\sqrt {1-k^{2}}}\right)\sin \varphi }{1+{\sqrt {1-k^{2}\sin ^{2}\varphi }}}},{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)}
F
(
φ
,
k
)
=
ln
tan
(
φ
∞
L
2
+
π
4
)
∏
n
=
0
∞
2
1
+
k
n
=
ln
tan
(
φ
∞
L
2
+
π
4
)
∏
n
=
0
∞
k
n
k
=
lim
n
→
∞
φ
−
n
L
∏
i
=
1
n
1
+
k
−
i
2
=
lim
n
→
∞
φ
−
n
L
k
−
n
k
∏
i
=
1
n
k
−
i
{\displaystyle F\left(\varphi ,k\right)=\ln \tan \left({\frac {\varphi _{\infty }^{L}}{2}}+{\frac {\pi }{4}}\right)\prod _{n=0}^{\infty }{\frac {2}{1+k_{n}}}=\ln \tan \left({\frac {\varphi _{\infty }^{L}}{2}}+{\frac {\pi }{4}}\right){\frac {\sqrt {\prod _{n=0}^{\infty }k_{n}}}{k}}=\lim \limits _{n\rightarrow \infty }\varphi _{-n}^{L}\prod _{i=1}^{n}{\frac {1+k_{-i}}{2}}=\lim \limits _{n\rightarrow \infty }\varphi _{-n}^{L}{\frac {k_{-n}}{k{\sqrt {\prod _{i=1}^{n}k_{-i}}}}}}
F
(
φ
,
k
)
=
lim
n
→
∞
ln
tan
(
φ
n
G
2
+
π
4
)
∏
i
=
0
n
1
1
+
k
i
=
lim
n
→
∞
ln
tan
(
φ
n
G
2
+
π
4
)
∏
i
=
0
n
k
n
2
n
k
=
φ
−
∞
G
∏
n
=
1
∞
(
1
+
k
−
n
)
=
φ
−
∞
G
lim
n
→
∞
2
n
k
−
n
k
∏
i
=
1
n
k
−
i
{\displaystyle F\left(\varphi ,k\right)=\lim \limits _{n\rightarrow \infty }\ln \tan \left({\frac {\varphi _{n}^{G}}{2}}+{\frac {\pi }{4}}\right)\prod _{i=0}^{n}{\frac {1}{1+k_{i}}}=\lim \limits _{n\rightarrow \infty }\ln \tan \left({\frac {\varphi _{n}^{G}}{2}}+{\frac {\pi }{4}}\right){\frac {\sqrt {\prod _{i=0}^{n}k_{n}}}{2^{n}k}}=\varphi _{-\infty }^{G}\prod _{n=1}^{\infty }\left(1+k_{-n}\right)=\varphi _{-\infty }^{G}\lim \limits _{n\rightarrow \infty }{\frac {2^{n}k_{-n}}{k{\sqrt {\prod _{i=1}^{n}k_{-i}}}}}}
Transformations de Landen des intégrales elliptiques de deuxième espèce
Transformation décroissante
Landen
E
(
φ
,
k
)
=
1
+
1
−
k
2
2
E
(
arccos
1
−
(
1
+
1
−
k
2
)
sin
2
φ
1
−
k
2
sin
2
φ
,
1
−
1
−
k
2
1
+
1
−
k
2
)
−
1
−
k
2
1
+
1
−
k
2
F
(
arccos
1
−
(
1
+
1
−
k
2
)
sin
2
φ
1
−
k
2
sin
2
φ
,
1
−
1
−
k
2
1
+
1
−
k
2
)
+
k
2
sin
(
2
φ
)
4
1
−
k
2
sin
2
φ
{\displaystyle \textstyle E\left(\varphi ,k\right)={\frac {1+{\sqrt {1-k^{2}}}}{2}}E\left(\arccos {\frac {1-\left(1+{\sqrt {1-k^{2}}}\right)\sin ^{2}\varphi }{\sqrt {1-k^{2}\sin ^{2}\varphi }}},{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)-{\frac {\sqrt {1-k^{2}}}{1+{\sqrt {1-k^{2}}}}}F\left(\arccos {\frac {1-\left(1+{\sqrt {1-k^{2}}}\right)\sin ^{2}\varphi }{\sqrt {1-k^{2}\sin ^{2}\varphi }}},{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)+{\frac {k^{2}\sin \left(2\varphi \right)}{4{\sqrt {1-k^{2}\sin ^{2}\varphi }}}}}
E
(
φ
,
k
)
=
[
1
−
k
2
2
(
∑
n
=
0
∞
∏
i
=
1
n
k
−
i
2
n
)
]
F
(
φ
,
k
)
+
k
∑
n
=
1
∞
∏
i
=
1
n
k
−
i
2
n
sin
φ
−
n
L
{\displaystyle E\left(\varphi ,k\right)=\left[1-{\frac {k^{2}}{2}}\left(\sum \limits _{n=0}^{\infty }\prod \limits _{i=1}^{n}{\frac {k_{-i}}{2^{n}}}\right)\right]F\left(\varphi ,k\right)+k\sum \limits _{n=1}^{\infty }{\frac {\sqrt {\prod \limits _{i=1}^{n}k_{-i}}}{2^{n}}}\sin \varphi _{-n}^{L}}
Transformations de Landen d'une fonction elliptique
Transformation croissante (Landen)
Transformation décroissante (Gauss)
sn
(
u
,
k
)
=
2
1
+
k
sn
(
1
+
k
2
u
,
2
k
1
+
k
)
cn
(
1
+
k
2
u
,
2
k
1
+
k
)
dn
(
1
+
k
2
u
,
2
k
1
+
k
)
{\displaystyle \operatorname {sn} \left(u,k\right)={\frac {{\tfrac {2}{1+k}}\operatorname {sn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)\operatorname {cn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)}{\operatorname {dn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)}}}
sn
(
u
,
k
)
=
2
1
+
1
−
k
2
sn
(
1
+
1
−
k
2
2
u
,
1
−
1
−
k
2
1
+
1
−
k
2
)
1
+
1
−
1
−
k
2
1
+
1
−
k
2
sn
2
(
1
+
1
−
k
2
2
u
,
1
−
1
−
k
2
1
+
1
−
k
2
)
{\displaystyle \operatorname {sn} \left(u,k\right)={\frac {{\tfrac {2}{1+{\sqrt {1-k^{2}}}}}\operatorname {sn} \left({\tfrac {1+{\sqrt {1-k^{2}}}}{2}}u,{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)}{1+{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\operatorname {sn} ^{2}\left({\tfrac {1+{\sqrt {1-k^{2}}}}{2}}u,{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)}}}
cn
(
u
,
k
)
=
dn
2
(
1
+
k
2
u
,
2
k
1
+
k
)
−
1
−
k
1
+
k
2
k
1
+
k
dn
(
1
+
k
2
u
,
2
k
1
+
k
)
{\displaystyle \operatorname {cn} \left(u,k\right)={\frac {\operatorname {dn} ^{2}\left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)-{\tfrac {1-k}{1+k}}}{{\tfrac {2k}{1+k}}\operatorname {dn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)}}}
cn
(
u
,
k
)
=
cn
(
1
+
1
−
k
2
2
u
,
1
−
1
−
k
2
1
+
1
−
k
2
)
dn
(
1
+
1
−
k
2
2
u
,
1
−
1
−
k
2
1
+
1
−
k
2
)
1
+
1
−
1
−
k
2
1
+
1
−
k
2
sn
2
(
1
+
1
−
k
2
2
u
,
1
−
1
−
k
2
1
+
1
−
k
2
)
{\displaystyle \operatorname {cn} \left(u,k\right)={\frac {\operatorname {cn} \left({\tfrac {1+{\sqrt {1-k^{2}}}}{2}}u,{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)\operatorname {dn} \left({\tfrac {1+{\sqrt {1-k^{2}}}}{2}}u,{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)}{1+{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\operatorname {sn} ^{2}\left({\tfrac {1+{\sqrt {1-k^{2}}}}{2}}u,{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)}}}
dn
(
u
,
k
)
=
dn
2
(
1
+
k
2
u
,
2
k
1
+
k
)
+
1
−
k
1
+
k
2
1
+
k
dn
(
1
+
k
2
u
,
2
k
1
+
k
)
{\displaystyle \operatorname {dn} \left(u,k\right)={\frac {\operatorname {dn} ^{2}\left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)+{\tfrac {1-k}{1+k}}}{{\tfrac {2}{1+k}}\operatorname {dn} \left({\tfrac {1+k}{2}}u,{\tfrac {2{\sqrt {k}}}{1+k}}\right)}}}
dn
(
u
,
k
)
=
1
−
1
−
k
2
1
+
1
−
k
2
−
(
1
−
dn
2
(
1
+
1
−
k
2
2
u
,
1
−
1
−
k
2
1
+
1
−
k
2
)
)
1
−
1
−
k
2
1
+
1
−
k
2
+
(
1
−
dn
2
(
1
+
1
−
k
2
2
u
,
1
−
1
−
k
2
1
+
1
−
k
2
)
)
{\displaystyle \operatorname {dn} \left(u,k\right)={\frac {{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}-\left(1-\operatorname {dn} ^{2}\left({\tfrac {1+{\sqrt {1-k^{2}}}}{2}}u,{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)\right)}{{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}+\left(1-\operatorname {dn} ^{2}\left({\tfrac {1+{\sqrt {1-k^{2}}}}{2}}u,{\tfrac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)\right)}}}
Intégrale elliptique complète de première espèce [ modifier | modifier le code ] L’intégrale elliptique complète de première espèce,
∀
k
2
∈
]
−
∞
;
1
[
{\displaystyle \forall k^{2}\in ]-\infty ;1[}
K
(
k
)
=
∫
θ
=
0
π
/
2
1
1
−
k
2
sin
2
θ
d
θ
=
π
2
∑
n
=
0
∞
[
P
2
n
(
0
)
]
2
k
2
n
=
π
2
∑
n
=
0
∞
[
CBC
(
n
)
2
2
n
]
2
k
2
n
=
π
2
∑
n
=
0
∞
[
C
2
n
n
2
2
n
]
2
k
2
n
=
π
2
∑
n
=
0
∞
[
(
2
n
−
1
)
!
!
(
2
n
)
!
!
]
2
k
2
n
=
π
2
∑
n
=
0
∞
[
(
2
n
)
!
2
2
n
n
!
2
]
2
k
2
n
{\displaystyle {\begin{aligned}K(k)&=\int \limits _{\theta =0}^{\pi /2}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}\,\mathrm {d} \theta ={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[P_{2n}\left(0\right)\right]^{2}k^{2n}\\&={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {\operatorname {CBC} \left(n\right)}{2^{2n}}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {C_{2n}^{n}}{2^{2n}}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {\left(2n\right)!}{2^{2n}n!^{2}}}\right]^{2}k^{2n}\end{aligned}}}
où :
Démonstration
On démontre par récurrence que, pour
i
∈
N
{\displaystyle i\in \mathbb {N} }
∂
k
i
i
1
1
−
k
2
sin
2
θ
=
∑
j
=
0
⌊
i
/
2
⌋
2
j
j
!
[
C
⌊
i
/
2
⌋
j
]
2
[
∏
m
=
1
⌊
(
i
+
1
)
/
2
⌋
(
2
m
−
1
)
1
+
[
m
>
j
+
(
i
−
2
⌊
i
/
2
⌋
)
]
]
k
2
j
+
(
i
−
2
⌊
i
/
2
⌋
)
sin
i
+
2
j
+
(
i
−
2
⌊
i
/
2
⌋
)
θ
(
1
−
k
2
sin
2
θ
)
(
2
i
+
1
)
/
2
{\displaystyle \partial _{k^{i}}^{i}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}={\frac {\sum \limits _{j=0}^{\lfloor {i/2}\rfloor }2^{j}j!\left[C_{\lfloor {i/2}\rfloor }^{j}\right]^{2}\left[\prod \limits _{m=1}^{\lfloor \left(i+1\right)/2\rfloor }(2m-1)^{1+\left[m>j+\left(i-2\lfloor {i/2}\rfloor \right)\right]}\right]k^{2j+\left(i-2\lfloor {i/2}\rfloor \right)}\sin ^{i+2j+\left(i-2\lfloor {i/2}\rfloor \right)}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}}
⇔
{
i
pair
:
∂
k
i
i
1
1
−
k
2
sin
2
θ
=
∑
j
=
0
i
/
2
2
j
j
!
[
C
i
/
2
j
]
2
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
sin
i
+
2
j
θ
(
1
−
k
2
sin
2
θ
)
(
2
i
+
1
)
/
2
i
impair
:
∂
k
i
i
1
1
−
k
2
sin
2
θ
=
∑
j
=
0
(
i
−
1
)
/
2
2
j
j
!
[
C
(
i
−
1
)
/
2
j
]
2
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
+
1
sin
i
+
2
j
+
1
θ
(
1
−
k
2
sin
2
θ
)
(
2
i
+
1
)
/
2
{\displaystyle \Leftrightarrow {\begin{cases}i{\text{ pair }}&:\partial _{k^{i}}^{i}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}={\frac {\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\i{\text{ impair }}&:\partial _{k^{i}}^{i}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}={\frac {\sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+1}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\end{cases}}}
car pour
i
=
0
{\displaystyle i=0}
i
=
1
{\displaystyle i=1}
{
∂
k
0
0
1
1
−
k
2
sin
2
θ
=
∑
j
=
0
0
[
∏
m
=
1
0
(
2
m
−
1
)
1
+
[
m
>
0
]
]
(
1
−
k
2
sin
2
θ
)
1
/
2
∂
k
1
1
1
1
−
k
2
sin
2
θ
=
∑
j
=
0
0
[
∏
m
=
1
1
(
2
m
−
1
)
1
+
[
m
>
1
]
]
k
sin
2
θ
(
1
−
k
2
sin
2
θ
)
3
/
2
{\displaystyle {\begin{cases}\partial _{k^{0}}^{0}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}&={\frac {\sum \limits _{j=0}^{0}\left[\prod \limits _{m=1}^{0}(2m-1)^{1+\left[m>0\right]}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{1/2}}}\\\partial _{k^{1}}^{1}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}&={\frac {\sum \limits _{j=0}^{0}\left[\prod \limits _{m=1}^{1}(2m-1)^{1+\left[m>1\right]}\right]k\sin ^{2}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{3/2}}}\end{cases}}}
et, pour
i
=
i
+
1
{\displaystyle i=i+1}
i
{\displaystyle i}
∂
k
i
+
1
i
+
1
1
1
−
k
2
sin
2
θ
=
[
(
1
−
k
2
sin
2
θ
)
∑
j
=
0
i
/
2
2
j
j
!
[
C
i
/
2
j
]
2
(
2
j
)
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
−
1
sin
i
+
2
j
θ
+
(
2
i
+
1
)
k
sin
2
θ
∑
j
=
0
i
/
2
2
j
j
!
[
C
i
/
2
j
]
2
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
sin
i
+
2
j
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
[
∑
j
=
0
i
/
2
2
j
j
!
[
C
i
/
2
j
]
2
(
2
j
)
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
−
1
sin
i
+
2
j
θ
+
∑
j
=
0
i
/
2
2
j
j
!
[
C
i
/
2
j
]
2
(
2
i
−
2
j
+
1
)
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
+
1
sin
i
+
2
j
+
2
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
[
∑
j
′
=
j
−
1
=
0
i
/
2
−
1
2
j
′
+
1
(
j
′
+
1
)
!
[
C
i
/
2
j
′
+
1
]
2
(
2
j
′
+
2
)
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
′
+
1
]
]
k
2
j
′
+
1
sin
i
+
2
j
′
+
2
θ
+
∑
j
=
0
i
/
2
2
j
j
!
[
C
i
/
2
j
]
2
(
2
i
−
2
j
+
1
)
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
+
1
sin
i
+
2
j
+
2
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
[
∑
j
=
0
i
/
2
−
1
2
j
j
!
[
C
i
/
2
j
]
2
[
[
i
/
2
−
j
j
+
1
]
2
(
2
j
+
2
)
2
+
(
2
i
−
2
j
+
1
)
(
2
j
+
1
)
]
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
+
1
sin
i
+
2
j
+
2
θ
+
∑
j
=
i
/
2
i
/
2
2
j
j
!
[
C
i
/
2
j
]
2
(
i
+
1
)
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
+
1
sin
i
+
2
j
+
2
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
[
∑
j
=
0
i
/
2
−
1
2
j
j
!
[
C
i
/
2
j
]
2
[
(
i
−
2
j
)
2
+
(
2
i
−
2
j
+
1
)
(
2
j
+
1
)
]
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
+
1
sin
i
+
2
j
+
2
θ
+
∑
j
=
i
/
2
i
/
2
2
j
j
!
[
C
i
/
2
j
]
2
(
i
+
1
)
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
+
1
sin
i
+
2
j
+
2
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
[
∑
j
=
0
i
/
2
−
1
2
j
j
!
[
C
i
/
2
j
]
2
(
i
+
1
)
2
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
+
1
sin
i
+
2
j
+
2
θ
+
∑
j
=
i
/
2
i
/
2
2
j
j
!
[
C
i
/
2
j
]
2
(
i
+
1
)
[
∏
m
=
1
i
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
+
1
sin
i
+
2
j
+
2
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
∑
j
=
0
i
/
2
2
j
j
!
[
C
i
/
2
j
]
2
[
∏
m
=
1
i
/
2
+
1
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
+
1
sin
i
+
2
j
+
2
θ
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
{\displaystyle {\begin{aligned}\partial _{k^{i+1}}^{i+1}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}&={\frac {\left[{\begin{matrix}\left(1-k^{2}\sin ^{2}\theta \right)\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2j\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j-1}\sin ^{i+2j}\theta \\+\left(2i+1\right)k\sin ^{2}\theta \sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2j\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j-1}\sin ^{i+2j}\theta \\+\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2i-2j+1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j'=j-1=0}^{i/2-1}2^{j'+1}\left(j'+1\right)!\left[C_{i/2}^{j'+1}\right]^{2}\left(2j'+2\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j'+1\right]}\right]k^{2j'+1}\sin ^{i+2j'+2}\theta \\+\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2i-2j+1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2-1}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\left[{\frac {i/2-j}{j+1}}\right]^{2}\left(2j+2\right)^{2}+\left(2i-2j+1\right)\left(2j+1\right)\right]\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \\+\sum \limits _{j=i/2}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(i+1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2-1}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\left(i-2j\right)^{2}+\left(2i-2j+1\right)\left(2j+1\right)\right]\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \\+\sum \limits _{j=i/2}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(i+1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2-1}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(i+1\right)^{2}\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \\+\sum \limits _{j=i/2}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(i+1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2+1}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\end{aligned}}}
et si i est impair, on a :
∂
k
i
+
1
i
+
1
1
1
−
k
2
sin
2
θ
=
[
(
1
−
k
2
sin
2
θ
)
∑
j
=
0
(
i
−
1
)
/
2
2
j
j
!
[
C
(
i
−
1
)
/
2
j
]
2
(
2
j
+
1
)
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
sin
i
+
2
j
+
1
θ
+
(
2
i
+
1
)
k
sin
2
θ
∑
j
=
0
(
i
−
1
)
/
2
2
j
j
!
[
C
(
i
−
1
)
/
2
j
]
2
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
+
1
sin
i
+
2
j
+
1
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
[
∑
j
=
0
(
i
−
1
)
/
2
2
j
j
!
[
C
(
i
−
1
)
/
2
j
]
2
(
2
j
+
1
)
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
sin
i
+
2
j
+
1
θ
+
∑
j
=
0
(
i
−
1
)
/
2
2
j
j
!
[
C
(
i
−
1
)
/
2
j
]
2
(
2
i
−
2
j
)
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
+
2
sin
i
+
2
j
+
3
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
[
∑
j
=
0
(
i
−
1
)
/
2
2
j
j
!
[
C
(
i
−
1
)
/
2
j
]
2
(
2
j
+
1
)
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
+
1
]
]
k
2
j
sin
i
+
2
j
+
1
θ
+
∑
j
′
=
j
+
1
=
1
(
i
+
1
)
/
2
2
j
′
−
1
(
j
′
−
1
)
!
[
C
(
i
−
1
)
/
2
j
′
−
1
]
2
(
2
i
−
2
j
′
+
2
)
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
′
]
]
k
2
j
′
sin
i
+
2
j
′
+
1
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
[
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
0
]
]
sin
i
+
1
θ
+
∑
j
=
1
(
i
−
1
)
/
2
2
j
j
!
[
C
(
i
+
1
)
/
2
j
]
2
[
[
(
i
+
1
)
/
2
−
j
(
i
+
1
)
/
2
]
2
+
[
j
(
i
+
1
)
/
2
]
2
1
2
j
(
2
i
−
2
j
+
2
)
]
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
sin
i
+
2
j
+
1
θ
+
∑
j
=
(
i
+
1
)
/
2
(
i
+
1
)
/
2
2
j
j
!
[
C
(
i
+
1
)
/
2
j
]
2
[
j
(
i
+
1
)
/
2
]
2
1
2
j
(
2
i
−
2
j
+
2
)
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
sin
i
+
2
j
+
1
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
[
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
0
]
]
sin
i
+
1
θ
+
∑
j
=
1
(
i
−
1
)
/
2
2
j
j
!
[
C
(
i
+
1
)
/
2
j
]
2
(
i
+
1
−
2
j
)
2
+
2
j
(
2
i
−
2
j
+
2
)
(
i
+
1
)
2
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
sin
i
+
2
j
+
1
θ
+
∑
j
=
(
i
+
1
)
/
2
(
i
+
1
)
/
2
2
j
j
!
[
C
(
i
+
1
)
/
2
j
]
2
2
j
(
2
i
−
2
j
+
2
)
(
i
+
1
)
2
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
sin
i
+
2
j
+
1
θ
]
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
=
∑
j
=
0
(
i
+
1
)
/
2
2
j
j
!
[
C
(
i
+
1
)
/
2
j
]
2
[
∏
m
=
1
(
i
+
1
)
/
2
(
2
m
−
1
)
1
+
[
m
>
j
]
]
k
2
j
sin
i
+
2
j
+
1
θ
(
1
−
k
2
sin
2
θ
)
(
2
i
+
3
)
/
2
{\displaystyle {\begin{aligned}\partial _{k^{i+1}}^{i+1}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}&={\frac {\left[{\begin{matrix}\left(1-k^{2}\sin ^{2}\theta \right)\sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2j+1\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\left(2i+1\right)k\sin ^{2}\theta \sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2j+1\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2i-2j\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+2}\sin ^{i+2j+3}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2j+1\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j'=j+1=1}^{\left(i+1\right)/2}2^{j'-1}\left(j'-1\right)!\left[C_{\left(i-1\right)/2}^{j'-1}\right]^{2}\left(2i-2j'+2\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j'\right]}\right]k^{2j'}\sin ^{i+2j'+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>0\right]}\right]\sin ^{i+1}\theta \\+\sum \limits _{j=1}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}\left[\left[{\frac {\left(i+1\right)/2-j}{\left(i+1\right)/2}}\right]^{2}+\left[{\frac {j}{\left(i+1\right)/2}}\right]^{2}{\frac {1}{2j}}\left(2i-2j+2\right)\right]\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j=\left(i+1\right)/2}^{\left(i+1\right)/2}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}\left[{\frac {j}{\left(i+1\right)/2}}\right]^{2}{\frac {1}{2j}}\left(2i-2j+2\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>0\right]}\right]\sin ^{i+1}\theta \\+\sum \limits _{j=1}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}{\frac {\left(i+1-2j\right)^{2}+2j\left(2i-2j+2\right)}{\left(i+1\right)^{2}}}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j=\left(i+1\right)/2}^{\left(i+1\right)/2}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}{\frac {2j\left(2i-2j+2\right)}{\left(i+1\right)^{2}}}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\sum \limits _{j=0}^{\left(i+1\right)/2}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\end{aligned}}}
Donc :
1
1
−
k
2
sin
2
θ
=
∑
i
=
0
∞
[
∏
m
=
1
i
(
2
m
−
1
)
2
]
sin
2
i
θ
k
2
i
(
2
i
)
!
=
∑
i
=
0
∞
(
2
i
)
!
2
2
i
i
!
2
k
2
i
sin
2
i
θ
=
∑
i
=
0
∞
C
2
i
i
2
2
i
k
2
i
sin
2
i
θ
{\displaystyle {\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}=\sum \limits _{i=0}^{\infty }{\frac {\left[\prod \limits _{m=1}^{i}\left(2m-1\right)^{2}\right]\sin ^{2i}\theta k^{2i}}{\left(2i\right)!}}=\sum \limits _{i=0}^{\infty }{\frac {\left(2i\right)!}{2^{2i}i!^{2}}}k^{2i}\sin ^{2i}\theta =\sum \limits _{i=0}^{\infty }{\frac {C_{2i}^{i}}{2^{2i}}}k^{2i}\sin ^{2i}\theta }
car :
lim
i
→
∞
(
2
i
)
!
2
2
i
i
!
2
=
∏
i
=
1
∞
(
1
−
1
2
i
)
=
e
∑
i
=
0
∞
ln
(
1
−
1
2
i
)
=
e
λ
i
0
+
∑
i
=
i
0
∞
ln
(
1
−
1
2
i
)
∼
e
λ
i
0
−
∑
i
=
i
0
∞
1
2
i
∼
e
λ
i
0
−
[
ln
i
2
]
i
0
∞
∼
0
{\displaystyle \lim \limits _{i\to \infty }{\frac {\left(2i\right)!}{2^{2i}i!^{2}}}=\prod \limits _{i=1}^{\infty }\left(1-{\frac {1}{2i}}\right)=\mathrm {e} ^{\sum \limits _{i=0}^{\infty }\ln \left(1-{\frac {1}{2i}}\right)}=\mathrm {e} ^{\lambda _{i_{0}}+\sum \limits _{i=i_{0}}^{\infty }\ln \left(1-{\frac {1}{2i}}\right)}\sim \mathrm {e} ^{\lambda _{i_{0}}-\sum \limits _{i=i_{0}}^{\infty }{\frac {1}{2i}}}\sim \mathrm {e} ^{\lambda _{i_{0}}-\left[{\frac {\ln {i}}{2}}\right]_{i_{0}}^{\infty }}\sim 0}
On a enfin :
∫
θ
=
0
π
/
2
sin
2
n
x
d
θ
=
∫
θ
=
0
π
/
2
(
e
i
x
−
e
−
i
x
2
i
)
2
n
d
θ
=
∫
θ
=
0
π
/
2
∑
j
=
0
2
n
C
2
n
j
(
−
1
)
j
e
i
(
2
n
−
2
j
)
x
2
2
n
(
−
1
)
n
d
θ
=
∫
θ
=
0
π
/
2
1
2
2
n
[
∑
j
=
0
n
−
1
(
−
1
)
j
C
2
n
j
e
i
(
2
n
−
2
j
)
x
+
e
−
i
(
2
n
−
2
j
)
x
(
−
1
)
n
+
C
2
n
n
]
d
θ
=
∫
θ
=
0
π
/
2
[
∑
j
=
0
n
−
1
(
−
1
)
n
+
j
C
2
n
j
cos
[
(
2
n
−
2
j
)
x
]
2
2
n
−
1
+
C
2
n
n
2
2
n
]
d
θ
=
[
∑
j
=
0
n
−
1
(
−
1
)
n
+
j
+
1
C
2
n
j
sin
[
(
2
n
−
2
j
)
x
]
2
2
n
−
1
(
2
n
−
2
j
)
+
C
2
n
n
2
2
n
θ
]
θ
=
0
π
/
2
=
π
2
C
2
n
n
2
2
n
{\displaystyle {\begin{aligned}\int \limits _{\theta =0}^{\pi /2}\sin ^{2n}x\,\mathrm {d} \theta &=\int \limits _{\theta =0}^{\pi /2}\left({\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2i}}\right)^{2n}\,\mathrm {d} \theta =\int \limits _{\theta =0}^{\pi /2}\sum \limits _{j=0}^{2n}C_{2n}^{j}{\frac {\left(-1\right)^{j}\mathrm {e} ^{\mathrm {i} \left(2n-2j\right)x}}{2^{2n}\left(-1\right)^{n}}}\,\mathrm {d} \theta \\&=\int \limits _{\theta =0}^{\pi /2}{\frac {1}{2^{2n}}}\left[\sum \limits _{j=0}^{n-1}\left(-1\right)^{j}C_{2n}^{j}{\frac {\mathrm {e} ^{\mathrm {i} \left(2n-2j\right)x}+\mathrm {e} ^{-\mathrm {i} \left(2n-2j\right)x}}{\left(-1\right)^{n}}}+C_{2n}^{n}\right]\mathrm {d} \theta \\&=\int \limits _{\theta =0}^{\pi /2}\left[\sum \limits _{j=0}^{n-1}{\frac {\left(-1\right)^{n+j}C_{2n}^{j}\cos \left[\left(2n-2j\right)x\right]}{2^{2n-1}}}+{\frac {C_{2n}^{n}}{2^{2n}}}\right]\mathrm {d} \theta \\&=\left[\sum \limits _{j=0}^{n-1}{\frac {\left(-1\right)^{n+j+1}C_{2n}^{j}\sin \left[\left(2n-2j\right)x\right]}{2^{2n-1}\left(2n-2j\right)}}+{\frac {C_{2n}^{n}}{2^{2n}}}\theta \right]_{\theta =0}^{\pi /2}={\frac {\pi }{2}}{\frac {C_{2n}^{n}}{2^{2n}}}\end{aligned}}}
Si
k
2
<
0
{\displaystyle k^{2}<0}
k
∈
]
0
;
1
[
{\displaystyle k\in ]0;1[}
K
(
i
k
)
=
∫
θ
=
0
π
/
2
1
1
+
k
2
sin
2
θ
d
θ
=
2
1
+
1
+
k
2
K
(
1
+
k
2
−
1
1
+
k
2
+
1
)
{\displaystyle K\left(\mathrm {i} k\right)=\int \limits _{\theta =0}^{\pi /2}{\frac {1}{\sqrt {1+k^{2}\sin ^{2}\theta }}}\,\mathrm {d} \theta ={\frac {2}{1+{\sqrt {1+k^{2}}}}}K\left({\frac {{\sqrt {1+k^{2}}}-1}{{\sqrt {1+k^{2}}}+1}}\right)}
Intégrale elliptique complète de deuxième espèce [ modifier | modifier le code ] L’intégrale elliptique complète de deuxième espèce,
∀
k
2
∈
]
−
∞
;
1
]
{\displaystyle \forall k^{2}\in ]-\infty ;1]}
E
(
k
)
=
∫
θ
=
0
π
/
2
1
−
k
2
sin
2
θ
d
θ
=
π
2
∑
n
=
0
∞
1
1
−
2
n
[
P
2
n
(
0
)
]
2
k
2
n
=
π
2
∑
n
=
0
∞
1
1
−
2
n
[
CBC
(
n
)
2
2
n
]
2
k
2
n
=
π
2
∑
n
=
0
∞
1
1
−
2
n
[
C
2
n
n
2
2
n
]
2
k
2
n
=
π
2
∑
n
=
0
∞
1
1
−
2
n
[
(
2
n
−
1
)
!
!
(
2
n
)
!
!
]
2
k
2
n
=
π
2
∑
n
=
0
∞
1
1
−
2
n
[
(
2
n
)
!
2
2
n
n
!
2
]
2
k
2
n
{\displaystyle {\begin{aligned}E(k)&=\int \limits _{\theta =0}^{\pi /2}{\sqrt {1-k^{2}\sin ^{2}\theta }}\,\mathrm {d} \theta ={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {1}{1-2n}}\left[P_{2n}\left(0\right)\right]^{2}k^{2n}\\&={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {1}{1-2n}}\left[{\frac {\operatorname {CBC} \left(n\right)}{2^{2n}}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {1}{1-2n}}\left[{\frac {C_{2n}^{n}}{2^{2n}}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {1}{1-2n}}\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {1}{1-2n}}\left[{\frac {\left(2n\right)!}{2^{2n}n!^{2}}}\right]^{2}k^{2n}\end{aligned}}}
Si
k
2
<
0
{\displaystyle k^{2}<0}
k
∈
]
0
;
1
[
{\displaystyle k\in ]0;1[}
E
(
i
k
)
=
∫
θ
=
0
π
/
2
1
+
k
2
sin
2
θ
d
θ
=
(
1
+
1
+
k
2
)
E
(
1
+
k
2
−
1
1
+
k
2
+
1
)
−
1
+
k
2
K
(
k
)
{\displaystyle E\left(\mathrm {i} k\right)=\int \limits _{\theta =0}^{\pi /2}{\sqrt {1+k^{2}\sin ^{2}\theta }}\,\mathrm {d} \theta =\left(1+{\sqrt {1+k^{2}}}\right)E\left({\frac {{\sqrt {1+k^{2}}}-1}{{\sqrt {1+k^{2}}}+1}}\right)-{\sqrt {1+k^{2}}}K\left(k\right)}
Intégrale elliptique incomplète de première espèce [ modifier | modifier le code ] L'intégrale elliptique incomplète de première espèce a le théorème d'addition suivant :
F
(
φ
1
,
k
)
+
F
(
φ
2
,
k
)
=
F
(
arctan
(
tan
φ
1
1
−
k
2
sin
2
φ
2
)
+
arctan
(
tan
φ
2
1
−
k
2
sin
2
φ
1
)
,
k
)
{\displaystyle F\left(\varphi _{1},k\right)+F\left(\varphi _{2},k\right)=F\left(\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right),k\right)}
Démonstration
Une démonstration s'appuie sur le théorème suivant :
f
(
φ
2
)
=
g
(
φ
2
)
⇔
{
f
(
0
)
=
g
(
0
)
et
∂
φ
2
f
(
φ
2
)
=
∂
φ
2
g
(
φ
2
)
{\displaystyle f(\varphi _{2})=g(\varphi _{2})\Leftrightarrow {\begin{cases}f(0)=g(0)\\{\text{et }}\partial _{\varphi _{2}}f(\varphi _{2})=\partial _{\varphi _{2}}g(\varphi _{2})\end{cases}}}
L'équation est vraie pour
φ
2
=
0
{\displaystyle \varphi _{2}=0}
1
1
−
k
2
sin
2
φ
2
=
∂
φ
2
[
arctan
(
tan
φ
1
1
−
k
2
sin
2
φ
2
)
+
arctan
(
tan
φ
2
1
−
k
2
sin
2
φ
1
)
]
1
−
k
2
sin
2
[
arctan
(
tan
φ
1
1
−
k
2
sin
2
φ
2
)
+
arctan
(
tan
φ
2
1
−
k
2
sin
2
φ
1
]
)
=
−
k
2
tan
φ
1
cos
φ
2
sin
φ
2
[
1
+
tan
2
φ
1
(
1
−
k
2
sin
2
φ
2
)
]
1
−
k
2
sin
2
φ
2
+
1
−
k
2
sin
2
φ
1
[
1
+
tan
2
φ
2
(
1
−
k
2
sin
2
φ
1
)
]
cos
2
φ
2
1
−
k
2
[
tan
φ
1
1
−
k
2
sin
2
φ
2
+
tan
φ
2
1
−
k
2
sin
2
φ
1
1
+
tan
2
φ
1
(
1
−
k
2
sin
2
φ
2
)
1
+
tan
2
φ
2
(
1
−
k
2
sin
2
φ
1
)
]
2
=
−
k
2
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
+
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
(
1
−
k
2
sin
2
φ
1
sin
2
φ
2
)
1
−
k
2
sin
2
φ
2
1
−
k
2
[
cos
φ
2
sin
φ
1
1
−
k
2
sin
2
φ
2
+
cos
φ
1
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
1
sin
2
φ
2
]
2
=
−
k
2
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
+
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
(
1
−
k
2
sin
2
φ
1
sin
2
φ
2
)
2
−
k
2
cos
2
φ
2
sin
2
φ
1
(
1
−
k
2
sin
2
φ
2
)
−
k
2
cos
2
φ
1
sin
2
φ
2
(
1
−
k
2
sin
2
φ
1
)
−
2
k
2
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
1
−
k
2
sin
2
φ
2
=
−
k
2
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
+
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
1
−
k
2
(
sin
2
φ
1
+
sin
2
φ
2
)
+
k
4
sin
2
φ
1
sin
2
φ
2
(
cos
2
φ
1
+
cos
2
φ
2
+
sin
2
φ
1
sin
2
φ
2
)
−
2
k
2
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
1
−
k
2
sin
2
φ
2
=
1
1
−
k
2
sin
2
φ
2
{\displaystyle {\begin{aligned}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}&={\frac {\partial _{\varphi _{2}}\left[\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right)\right]}{\sqrt {1-k^{2}\sin ^{2}\left[\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right]\right)}}}\\&={\frac {{\frac {-k^{2}\tan \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}}{\left[1+\tan ^{2}\varphi _{1}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)\right]{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}+{\frac {\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\left[1+\tan ^{2}\varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{1}\right)\right]\cos ^{2}\varphi _{2}}}}{\sqrt {1-k^{2}\left[{\frac {\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}+\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}}{{\sqrt {1+\tan ^{2}\varphi _{1}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)}}{\sqrt {1+\tan ^{2}\varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{1}\right)}}}}\right]^{2}}}}\\&={\frac {\frac {-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right){\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}{\sqrt {1-k^{2}\left[{\frac {\cos \varphi _{2}\sin \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}+\cos \varphi _{1}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}}{1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}}}\right]^{2}}}}\\&={\frac {\frac {-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{\sqrt {\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)^{2}-k^{2}\cos ^{2}\varphi _{2}\sin ^{2}\varphi _{1}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)-k^{2}\cos ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{1}\right)-2k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}\\&={\frac {\frac {-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{\sqrt {1-k^{2}\left(\sin ^{2}\varphi _{1}+\sin ^{2}\varphi _{2}\right)+k^{4}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\left(\cos ^{2}\varphi _{1}+\cos ^{2}\varphi _{2}+\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)-2k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}\\&={\frac {1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}\end{aligned}}}
On a ensuite :
arctan
(
tan
φ
1
1
−
k
2
sin
2
φ
2
)
+
arctan
(
tan
φ
2
1
−
k
2
sin
2
φ
1
)
=
arcsin
tan
φ
2
1
−
k
2
sin
2
φ
1
+
tan
φ
1
1
−
k
2
sin
2
φ
2
1
+
tan
2
φ
1
(
1
−
k
2
sin
2
φ
2
)
1
+
tan
2
φ
2
(
1
−
k
2
sin
2
φ
1
)
=
arcsin
cos
φ
1
1
−
k
2
sin
2
φ
1
sin
φ
2
+
cos
φ
2
1
−
k
2
sin
2
φ
2
sin
φ
1
1
−
k
2
sin
2
φ
1
sin
2
φ
2
=
arccos
1
−
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
1
−
k
2
sin
2
φ
1
sin
2
φ
2
{\displaystyle {\begin{aligned}\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right)\\=\arcsin {\frac {\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}+\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{{\sqrt {1+\tan ^{2}\varphi _{1}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)}}{\sqrt {1+\tan ^{2}\varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{1}\right)}}}}\\=\arcsin {\frac {\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}}{1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}}}\\=\arccos {\frac {1-\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}}}\end{aligned}}}
On a ensuite, selon les circonstances (c.-à-d. en tenant compte du fait que
arcsin
x
∈
[
−
π
/
2
;
π
/
2
]
{\displaystyle \arcsin x\in [-\pi /2;\pi /2]}
arccos
x
∈
[
0
;
π
]
{\displaystyle \arccos x\in [0;\pi ]}
F
(
φ
1
,
k
)
+
F
(
φ
2
,
k
)
=
F
(
arctan
(
tan
φ
1
1
−
k
2
sin
2
φ
2
)
+
arctan
(
tan
φ
2
1
−
k
2
sin
2
φ
1
)
,
k
)
=
F
(
arcsin
cos
φ
1
1
−
k
2
sin
2
φ
1
sin
φ
2
+
cos
φ
2
1
−
k
2
sin
2
φ
2
sin
φ
1
1
−
k
2
sin
2
φ
1
sin
2
φ
2
,
k
)
=
F
(
arccos
1
−
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
1
−
k
2
sin
2
φ
1
sin
2
φ
2
,
k
)
{\displaystyle {\begin{aligned}F\left(\varphi _{1},k\right)+F\left(\varphi _{2},k\right)&=F\left(\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right),k\right)\\&=F\left(\arcsin {\frac {\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}}{1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}}},k\right)\\&=F\left(\arccos {\frac {1-\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}}},k\right)\end{aligned}}}
Intégrale elliptique incomplète de deuxième espèce [ modifier | modifier le code ] L'intégrale elliptique incomplète de deuxième espèce a le théorème d'addition suivant :
E
(
φ
1
,
k
)
+
E
(
φ
2
,
k
)
=
[
E
(
arctan
(
tan
φ
1
1
−
k
2
sin
2
φ
2
)
+
arctan
(
tan
φ
2
1
−
k
2
sin
2
φ
1
)
,
k
)
+
k
2
sin
φ
1
sin
φ
2
(
cos
φ
1
1
−
k
2
sin
2
φ
1
sin
φ
2
+
cos
φ
2
1
−
k
2
sin
2
φ
2
sin
φ
1
)
1
−
k
2
sin
φ
1
sin
φ
2
]
{\displaystyle \textstyle E\left(\varphi _{1},k\right)+E\left(\varphi _{2},k\right)=\left[{\begin{aligned}E\left(\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right),k\right)\\+{\frac {k^{2}\sin \varphi _{1}\sin \varphi _{2}\left(\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}\right)}{1-k^{2}\sin \varphi _{1}\sin \varphi _{2}}}\end{aligned}}\right]}
Démonstration
On procède de la même façon :
L'équation est vraie pour
φ
2
=
0
{\displaystyle \varphi _{2}=0}
1
−
k
2
sin
2
φ
2
=
[
(
−
k
2
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
+
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
)
2
+
k
2
sin
φ
1
[
(
1
−
k
2
sin
2
φ
1
sin
2
φ
2
)
×
[
cos
φ
2
[
sin
φ
1
cos
φ
2
(
1
−
k
2
sin
2
φ
2
)
+
cos
φ
1
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
]
+
sin
φ
2
[
−
sin
φ
1
sin
φ
2
(
1
−
k
2
sin
2
φ
2
)
−
k
2
sin
φ
1
cos
2
φ
2
sin
φ
2
+
cos
φ
1
cos
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
]
]
+
2
k
2
sin
2
φ
1
cos
φ
2
sin
2
φ
2
[
sin
φ
1
cos
φ
2
(
1
−
k
2
sin
2
φ
2
)
+
cos
φ
1
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
]
]
]
(
1
−
k
2
sin
2
φ
1
sin
2
φ
2
)
2
1
−
k
2
sin
2
φ
2
=
[
(
−
k
2
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
+
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
)
2
+
k
2
sin
φ
1
[
(
1
−
k
2
sin
2
φ
1
sin
2
φ
2
)
×
[
sin
φ
1
(
cos
2
φ
2
−
sin
2
φ
2
)
−
k
2
sin
φ
1
sin
2
φ
2
(
2
cos
2
φ
2
−
sin
2
φ
2
)
+
2
cos
φ
1
cos
φ
2
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
]
+
2
k
2
sin
2
φ
1
cos
φ
2
sin
2
φ
2
[
sin
φ
1
cos
φ
2
(
1
−
k
2
sin
2
φ
2
)
+
cos
φ
1
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
]
]
]
(
1
−
k
2
sin
2
φ
1
sin
2
φ
2
)
2
1
−
k
2
sin
2
φ
2
=
[
(
−
k
2
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
+
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
)
2
+
k
2
sin
φ
1
[
sin
φ
1
(
cos
2
φ
2
−
sin
2
φ
2
)
+
k
2
[
sin
φ
1
sin
2
φ
2
(
sin
2
φ
1
−
2
cos
2
φ
2
+
sin
2
φ
2
)
]
−
k
4
sin
3
φ
1
sin
6
φ
2
+
2
cos
φ
1
cos
φ
2
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
]
]
(
1
−
k
2
sin
2
φ
1
sin
2
φ
2
)
2
1
−
k
2
sin
2
φ
2
=
[
k
4
cos
2
φ
1
sin
2
φ
1
cos
2
φ
2
sin
2
φ
2
+
(
1
−
k
2
sin
2
φ
1
)
(
1
−
k
2
sin
2
φ
2
)
+
k
2
sin
2
φ
1
(
cos
2
φ
2
−
sin
2
φ
2
)
+
k
4
sin
2
φ
1
sin
2
φ
2
(
sin
2
φ
1
−
2
cos
2
φ
2
+
sin
2
φ
2
)
−
k
6
sin
4
φ
1
sin
6
φ
2
]
(
1
−
k
2
sin
2
φ
1
sin
2
φ
2
)
2
1
−
k
2
sin
2
φ
2
=
[
1
+
k
2
sin
2
φ
2
(
−
2
sin
2
φ
1
−
1
)
+
k
4
sin
2
φ
1
sin
2
φ
2
(
sin
2
φ
1
−
cos
2
φ
2
+
2
sin
2
φ
2
+
1
−
sin
2
φ
1
−
sin
2
φ
2
+
sin
2
φ
1
sin
2
φ
2
)
−
k
6
sin
4
φ
1
sin
6
φ
2
]
(
1
−
2
k
2
sin
2
φ
1
sin
2
φ
2
+
k
4
sin
4
φ
1
sin
4
φ
2
)
1
−
k
2
sin
2
φ
2
=
1
+
k
2
sin
2
φ
2
(
−
2
sin
2
φ
1
−
1
)
+
k
4
sin
2
φ
1
sin
4
φ
2
(
2
+
sin
2
φ
1
)
−
k
6
sin
4
φ
1
sin
6
φ
2
(
1
−
2
k
2
sin
2
φ
1
sin
2
φ
2
+
k
4
sin
4
φ
1
sin
4
φ
2
)
1
−
k
2
sin
2
φ
2
=
1
−
k
2
sin
2
φ
2
{\displaystyle \textstyle {\begin{aligned}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}&={\frac {\left[{\begin{matrix}\left(-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)^{2}\\+k^{2}\sin \varphi _{1}\left[{\begin{matrix}\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)\\\times \left[{\begin{matrix}\cos \varphi _{2}\left[\sin \varphi _{1}\cos \varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)+\cos \varphi _{1}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right]\\+\sin \varphi _{2}\left[{\begin{matrix}-\sin \varphi _{1}\sin \varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)-k^{2}\sin \varphi _{1}\cos ^{2}\varphi _{2}\sin \varphi _{2}\\+\cos \varphi _{1}\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\end{matrix}}\right]\end{matrix}}\right]\\+2k^{2}\sin ^{2}\varphi _{1}\cos \varphi _{2}\sin ^{2}\varphi _{2}\left[\sin \varphi _{1}\cos \varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)+\cos \varphi _{1}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right]\end{matrix}}\right]\end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)^{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\frac {\left[{\begin{matrix}\left(-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)^{2}\\+k^{2}\sin \varphi _{1}\left[{\begin{matrix}\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)\\\times \left[{\begin{matrix}\sin \varphi _{1}\left(\cos ^{2}\varphi _{2}-\sin ^{2}\varphi _{2}\right)-k^{2}\sin \varphi _{1}\sin ^{2}\varphi _{2}\left(2\cos ^{2}\varphi _{2}-\sin ^{2}\varphi _{2}\right)\\+2\cos \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\end{matrix}}\right]\\+2k^{2}\sin ^{2}\varphi _{1}\cos \varphi _{2}\sin ^{2}\varphi _{2}\left[\sin \varphi _{1}\cos \varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)+\cos \varphi _{1}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right]\end{matrix}}\right]\end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)^{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\frac {\left[{\begin{matrix}\left(-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)^{2}\\+k^{2}\sin \varphi _{1}\left[{\begin{matrix}\sin \varphi _{1}\left(\cos ^{2}\varphi _{2}-\sin ^{2}\varphi _{2}\right)\\+k^{2}\left[\sin \varphi _{1}\sin ^{2}\varphi _{2}\left(\sin ^{2}\varphi _{1}-2\cos ^{2}\varphi _{2}+\sin ^{2}\varphi _{2}\right)\right]\\-k^{4}\sin ^{3}\varphi _{1}\sin ^{6}\varphi _{2}\\+2\cos \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\end{matrix}}\right]\end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)^{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\frac {\left[{\begin{matrix}k^{4}\cos ^{2}\varphi _{1}\sin ^{2}\varphi _{1}\cos ^{2}\varphi _{2}\sin ^{2}\varphi _{2}+\left(1-k^{2}\sin ^{2}\varphi _{1}\right)\left(1-k^{2}\sin ^{2}\varphi _{2}\right)\\+k^{2}\sin ^{2}\varphi _{1}\left(\cos ^{2}\varphi _{2}-\sin ^{2}\varphi _{2}\right)\\+k^{4}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\left(\sin ^{2}\varphi _{1}-2\cos ^{2}\varphi _{2}+\sin ^{2}\varphi _{2}\right)\\-k^{6}\sin ^{4}\varphi _{1}\sin ^{6}\varphi _{2}\end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)^{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\frac {\left[{\begin{matrix}1+k^{2}\sin ^{2}\varphi _{2}\left(-2\sin ^{2}\varphi _{1}-1\right)\\+k^{4}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\left(\sin ^{2}\varphi _{1}-\cos ^{2}\varphi _{2}+2\sin ^{2}\varphi _{2}+1-\sin ^{2}\varphi _{1}-\sin ^{2}\varphi _{2}+\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)\\-k^{6}\sin ^{4}\varphi _{1}\sin ^{6}\varphi _{2}\end{matrix}}\right]}{\left(1-2k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}+k^{4}\sin ^{4}\varphi _{1}\sin ^{4}\varphi _{2}\right){\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\frac {1+k^{2}\sin ^{2}\varphi _{2}\left(-2\sin ^{2}\varphi _{1}-1\right)+k^{4}\sin ^{2}\varphi _{1}\sin ^{4}\varphi _{2}\left(2+\sin ^{2}\varphi _{1}\right)-k^{6}\sin ^{4}\varphi _{1}\sin ^{6}\varphi _{2}}{\left(1-2k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}+k^{4}\sin ^{4}\varphi _{1}\sin ^{4}\varphi _{2}\right){\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\end{aligned}}}
On a ensuite, selon les circonstances (c.-à-d. en tenant compte du fait que
arcsin
x
∈
[
−
π
/
2
;
π
/
2
]
{\displaystyle \arcsin x\in [-\pi /2;\pi /2]}
arccos
x
∈
[
0
;
π
]
{\displaystyle \arccos x\in [0;\pi ]}
E
(
φ
1
,
k
)
+
E
(
φ
2
,
k
)
=
[
E
(
arctan
(
tan
φ
1
1
−
k
2
sin
2
φ
2
)
+
arctan
(
tan
φ
2
1
−
k
2
sin
2
φ
1
)
,
k
)
+
k
2
sin
φ
1
sin
φ
2
(
cos
φ
1
1
−
k
2
sin
2
φ
1
sin
φ
2
+
cos
φ
2
1
−
k
2
sin
2
φ
2
sin
φ
1
)
1
−
k
2
sin
φ
1
sin
φ
2
]
=
[
E
(
arcsin
cos
φ
1
1
−
k
2
sin
2
φ
1
sin
φ
2
+
cos
φ
2
1
−
k
2
sin
2
φ
2
sin
φ
1
1
−
k
2
sin
2
φ
1
sin
2
φ
2
,
k
)
+
k
2
sin
φ
1
sin
φ
2
(
cos
φ
1
1
−
k
2
sin
2
φ
1
sin
φ
2
+
cos
φ
2
1
−
k
2
sin
2
φ
2
sin
φ
1
)
1
−
k
2
sin
φ
1
sin
φ
2
]
=
[
E
(
arccos
1
−
cos
φ
1
sin
φ
1
cos
φ
2
sin
φ
2
1
−
k
2
sin
2
φ
1
1
−
k
2
sin
2
φ
2
1
−
k
2
sin
2
φ
1
sin
2
φ
2
,
k
)
+
k
2
sin
φ
1
sin
φ
2
(
cos
φ
1
1
−
k
2
sin
2
φ
1
sin
φ
2
+
cos
φ
2
1
−
k
2
sin
2
φ
2
sin
φ
1
)
1
−
k
2
sin
φ
1
sin
φ
2
]
{\displaystyle \textstyle {\begin{aligned}E\left(\varphi _{1},k\right)+E\left(\varphi _{2},k\right)&=\left[{\begin{aligned}E\left(\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right),k\right)\\+{\frac {k^{2}\sin \varphi _{1}\sin \varphi _{2}\left(\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}\right)}{1-k^{2}\sin \varphi _{1}\sin \varphi _{2}}}\end{aligned}}\right]\\&=\left[{\begin{aligned}E\left(\arcsin {\frac {\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}}{1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}}},k\right)\\+{\frac {k^{2}\sin \varphi _{1}\sin \varphi _{2}\left(\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}\right)}{1-k^{2}\sin \varphi _{1}\sin \varphi _{2}}}\end{aligned}}\right]\\&=\left[{\begin{aligned}E\left(\arccos {\frac {1-\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}}},k\right)\\+{\frac {k^{2}\sin \varphi _{1}\sin \varphi _{2}\left(\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}\right)}{1-k^{2}\sin \varphi _{1}\sin \varphi _{2}}}\end{aligned}}\right]\end{aligned}}}
↑ Elliptic Integrals - Harris Hancock, John Wiley & Sons, New York (1917) ↑ Elliptic Integrals - Harris Hancock, John Wiley & Sons, New York (1917) - page 34 ↑ Elliptic Integrals - Harris Hancock, John Wiley & Sons, New York (1917) - page 28 ↑ Elliptic Integrals - Harris Hancock, John Wiley & Sons, New York (1917) - page 68 ↑ Elliptic Integrals - Harris Hancock, John Wiley & Sons, New York (1917) - page 74 ↑ Elliptic Integrals - Harris Hancock, John Wiley & Sons, New York (1917) - page 80 ↑ a et b Elliptic Integrals - Harris Hancock, John Wiley & Sons, New York (1917) - page 29
↑ DOI 10.1098/rstl.1775.0028 ↑ C. F. Gauss et Nachlass , « Arithmetisch geometrisches Mittel, Werke, Bd. 3 », Königlichen Gesell. Wiss., Göttingen , 1876 , p. 361–403 ↑ G.M. Scarpello, D. Ritelli and A. Scimone, The hyperbola rectification from Maclaurin to Landen and the Lagrange-Legendre transformation for the elliptic integrals
↑ ru:Обсуждение:Преобразование_Ландена ↑ H. McKean and V. Moll, Elliptic Curves: Function Theory, Geometry, Arithmetic ; Cambridge University Press, Cambridge (1997). (ISBN 0-521-65817-9 .
↑ Modèle:Dlmf ↑ Transformation de Landen ↑ A.L. Baker, Elliptic Functions - An Elementary Textbook for Students of Mathematics
↑ M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions (ISBN 0-486-61272-4 .
↑ G.N. Watson, The Marquis and the Land-Agent; A Tale of the Eighteenth Century 17 , 5-17 (1934). Foredrag for the British Mathematical Association, 1933. Gjengitt i J.J. Berggren, J. Borwein and P. Borwein, Pi: A Source Book , Springer-Verlag, New York (2004). (ISBN 978-1-4419-1915-1 .
↑ Elliptic Functions: Landen's Transformation ↑ de:Elliptische_Integrale#Landensche_Transformationen Louis V. King On The Direct Numerical Calculation Of Elliptic Functions And Integrals
Transformation de Landen Transformation de Gauss Manuel de fonctions mathématiques Notes mathématiques de Paramanand, Transformation de Landen . Blog mathématique.
Cayley A. Un traité élémentaire sur les fonctions elliptiques . — G. Bell et fils, 1895.
Almkvist G. , Berndt B.Gauss, Landen, Ramanujan, la moyenne arithmétique-géométrique, les ellipses, π et le Ladies Diary // The American Mathematical Monthly. - 1988. - Vol. 95 , P. 7 . - P. 585-608 . - ISSN 0002-9890 . - DOI : 10.1080/00029890.1988.11972055
Milne-Thomson L. Ch. 17. Intégrales elliptiques // Manuel de fonctions spéciales avec formules, graphiques et tableaux / Ed. M. Abramowitz et I. Stigan ; langue anglaise, édité par V. A. Ditkin et L. N. Karamzina. - M. : Nauka, 1979. - P. 401-441. — 832 p. — 50 000 exemplaires.
Korn G., Korn T. // Manuel de mathématiques destiné aux scientifiques et ingénieurs. M. : Nauka, 1977.
Sikorsky Yu. S. Éléments de la théorie des fonctions elliptiques : Avec application à la mécanique. — Éd. 2e, rév. - M. : Kom Book, 2006. - 368 p. 



![{\displaystyle k\in [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af7c443db3d15651b60d952db2656cac2d503361)



















![{\displaystyle \operatorname {zn} (u,k)=\int _{0}^{u}\left[\operatorname {dn} (t,k)^{2}-{\frac {E(k)}{K(k)}}\right]\,\mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b75249f39fbf2610fd3a4e7666e6718acabece2a)















![{\displaystyle {\begin{cases}&k_{n+1}&={\frac {2{\sqrt {k_{n}}}}{1+k_{n}}}&={\frac {2{\sqrt[{4}]{1-k_{n}'^{2}}}}{1+{\sqrt {1-k_{n}'^{2}}}}},&k_{n+1}'&={\frac {1-k_{n}}{1+k_{n}}}&={\frac {1-{\sqrt {1-k_{n}'^{2}}}}{1+{\sqrt {1-k_{n}'^{2}}}}}\\\Leftrightarrow &k_{n-1}&={\frac {1-{\sqrt {1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}&={\frac {1-k_{n}'}{1+k_{n}'}},&k_{n-1}'&={\frac {2{\sqrt[{4}]{1-k_{n}^{2}}}}{1+{\sqrt {1-k_{n}^{2}}}}}&={\frac {2{\sqrt {k_{n}'}}}{1+k_{n}'}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/462ddbf17654bec2d76cbbfa0e78bd34243ecd61)







![{\displaystyle \cos \theta _{n}\left[k_{n}+\cos \left(2\theta _{n+1}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3284c229f8d7d53f9ecf9f79d4cc2e76a6cdf36)



![{\displaystyle \mathrm {d} \theta _{n}=\cos ^{2}\theta _{n}\,\mathrm {d} \tan \theta _{n}={\frac {2\left[1+k_{n}\cos \left(2\theta _{n+1}\right)\right]}{1+k_{n}^{2}+2k_{n}\cos \left(2\theta _{n+1}\right)}}\mathrm {d} \theta _{n+1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdffd3256d8fa2cfb9291f13c821ddad869ba90d)





![{\displaystyle \Rightarrow \cos(2\varphi _{n+1}^{L})=-k_{n}\sin ^{2}\varphi _{n}^{L}\pm {\sqrt {k_{n}^{2}\sin ^{4}\varphi _{n}^{L}-k_{n}^{2}\sin ^{2}\varphi _{n}^{L}+1-\sin ^{2}\varphi _{n}^{L}}}\in \left[-1;+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb7c3115a7e8f500441feb9258ac016441d0b3a5)



![{\displaystyle \varphi _{n+1}^{L}\in \left[{\frac {\varphi _{n}^{L}}{2}};\varphi _{n}^{L}\right]\Leftrightarrow \varphi _{n}^{L}\in \left[\varphi _{n+1}^{L};2\varphi _{n+1}^{L}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e766078797c16ceb2ee58d7bc72761e322b9452)
![{\displaystyle {\begin{cases}\varphi _{n+1}^{L}\in \left[0;{\frac {\pi }{2}}-{\frac {\arccos k_{n}}{2}}\right]&\Leftrightarrow \varphi _{n}^{L}\in \left[0;{\frac {\pi }{2}}\right]\\\varphi _{n+1}^{L}\in \left[{\frac {\pi }{2}}-{\frac {\arccos k_{n}}{2}};{\frac {\pi }{2}}\right]&\Leftrightarrow \varphi _{n}^{L}\in \left[{\frac {\pi }{2}};\pi \right]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62f991ae06e3f6d717ee6df489f0750e4834770d)


![{\displaystyle \varphi _{n}^{L}\in \left]\pi /2;\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a40ac41f5991602242238cefecd80ac9b7fb21e9)























![{\displaystyle {\begin{array}{ccc}[0;\pi ]&\to &[0;\pi /2]\\\varphi _{n}^{L}&\mapsto &\varphi _{n+1}^{L}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0166ba48f5c289ace63eb8bce779f78c95b6bb1)
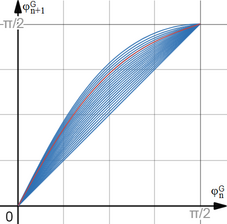
![{\displaystyle {\begin{array}{ccc}[0;\pi /2]&\to &[0;\pi /2]\\\varphi _{n}^{G}&\mapsto &\varphi _{n+1}^{G}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/512e1e23af589a01fd10cebf57de2915516d98e3)


![{\displaystyle k_{n}\in [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/171358c1bac7751c4e4cc8e915aee3ccef058caf)






















































![{\displaystyle E\left(a,b,\varphi \right)=\left[a^{2}-\sum \limits _{n=1}^{\infty }2^{n}a_{-n}c_{-n}\right]F\left(a,b,\varphi \right)+\sum \limits _{n=1}^{\infty }c_{-n}\sin \varphi _{-n}^{L}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59938d1a19d108104e7feb0901f5bb6885cba987)
![{\displaystyle {\begin{aligned}E\left(\varphi ,k\right)&=\left[1-\sum \limits _{n=1}^{\infty }{\frac {2^{n}a_{-n}c_{-n}}{a^{2}}}\right]F\left(\varphi ,k\right)+\sum \limits _{n=1}^{\infty }{\frac {c_{-n}}{a}}\sin \varphi _{-n}^{L}\\&=\left[1-{\frac {2a_{-1}c_{-1}}{a^{2}}}-{\frac {2a_{-1}c_{-1}}{a^{2}}}{\frac {2a_{-2}c_{-2}}{a_{-1}c_{-1}}}-{\frac {2a_{-1}c_{-1}}{a^{2}}}{\frac {2a_{-2}c_{-2}}{a_{-1}c_{-1}}}{\frac {2a_{-3}c_{-3}}{a_{-2}c_{-2}}}-\cdots \right]F\left(\varphi ,k\right)+\scriptstyle {\frac {c_{-1}}{a}}\displaystyle \sin \varphi _{-1}^{L}+\scriptstyle {\frac {a_{-1}}{a}}{\frac {c_{-2}}{a_{-1}}}\displaystyle \sin \varphi _{-2}^{L}+\scriptstyle {\frac {a_{-1}}{a}}{\frac {a_{-2}}{a_{-1}}}{\frac {c_{-3}}{a_{-2}}}\displaystyle \sin \varphi _{-3}^{L}+\cdots \\&=\left[1-{\frac {k^{2}}{2}}\left(1+{\frac {k_{-1}}{2}}+{\frac {k_{-1}k_{-2}}{4}}+{\frac {k_{-1}k_{-2}k_{-3}}{8}}+\cdots \right)\right]F\left(\varphi ,k\right)+\scriptstyle {\frac {k_{-1}}{1+k_{-1}}}\displaystyle \sin \varphi _{-1}^{L}+\scriptstyle {\frac {1}{1+k_{-1}}}{\frac {k_{-2}}{1+k_{-2}}}\displaystyle \sin \varphi _{-2}^{L}+\scriptstyle {\frac {1}{1+k_{-1}}}{\frac {1}{1+k_{-2}}}{\frac {k_{-3}}{1+k_{-3}}}\displaystyle \sin \varphi _{-3}^{L}+\cdots \\&=\left[1-{\frac {k^{2}}{2}}\left(\sum \limits _{n=0}^{\infty }\prod \limits _{i=1}^{n}{\frac {k_{-i}}{2^{n}}}\right)\right]F\left(\varphi ,k\right)+\sum \limits _{n=1}^{\infty }{\frac {k_{-n}}{\prod \limits _{i=1}^{n}\left(1+k_{-i}\right)}}\sin \varphi _{-n}^{L}\\&=\left[1-{\frac {k^{2}}{2}}\left(1+{\frac {k_{-1}}{2}}+{\frac {k_{-1}k_{-2}}{4}}+{\frac {k_{-1}k_{-2}k_{-3}}{8}}+\cdots \right)\right]F\left(\varphi ,k\right)+\scriptstyle k_{-1}{\frac {k}{2{\sqrt {k_{-1}}}}}\displaystyle \sin \varphi _{-1}^{L}+\scriptstyle k_{-2}{\frac {k}{2{\sqrt {k_{-1}}}}}{\frac {k_{-1}}{2{\sqrt {k_{-2}}}}}\displaystyle \sin \varphi _{-2}^{L}+\scriptstyle k_{-3}{\frac {k}{2{\sqrt {k_{-1}}}}}{\frac {k_{-1}}{2{\sqrt {k_{-2}}}}}{\frac {k_{-2}}{2{\sqrt {k_{-3}}}}}\displaystyle \sin \varphi _{-3}^{L}+\cdots \\&=\left[1-{\frac {k^{2}}{2}}\left(1+{\frac {k_{-1}}{2}}+{\frac {k_{-1}k_{-2}}{4}}+{\frac {k_{-1}k_{-2}k_{-3}}{8}}+\cdots \right)\right]F\left(\varphi ,k\right)+k\left[\scriptstyle {\frac {\sqrt {k_{-1}}}{2}}\displaystyle \sin \varphi _{-1}^{L}+\scriptstyle {\frac {\sqrt {k_{-1}k_{-2}}}{4}}\displaystyle \sin \varphi _{-2}^{L}+\scriptstyle {\frac {\sqrt {k_{-1}k_{-2}k_{-3}}}{8}}\displaystyle \sin \varphi _{-3}^{L}+\cdots \right]\\&=\left[1-{\frac {k^{2}}{2}}\left(\sum \limits _{n=0}^{\infty }\prod \limits _{i=1}^{n}{\frac {k_{-i}}{2^{n}}}\right)\right]F\left(\varphi ,k\right)+k\sum \limits _{n=1}^{\infty }{\frac {\sqrt {\prod \limits _{i=1}^{n}k_{-i}}}{2^{n}}}\sin \varphi _{-n}^{L}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70217b860eb691d08747750d8b65e04335e3777d)
![{\displaystyle E\left(k\right)=\left[1-{\frac {k^{2}}{2}}\left(\sum \limits _{n=0}^{\infty }\prod \limits _{i=1}^{n}{\frac {k_{-i}}{2^{n}}}\right)\right]K\left(k\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c88b8480de54f9c16f22356707b15a5d5ed90a3)





















![{\displaystyle K(k)\equiv {\frac {3\operatorname {sn} \left[{\tfrac {1}{3}}K(k),k\right]}{2-\operatorname {sn} \left[{\tfrac {1}{3}}K(k),k\right]}}K\left\{k^{3}\operatorname {sn} \left[{\tfrac {1}{3}}K(k),k\right]^{4}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4201333708a83eeb48453fc1c83a174682ae035f)
![{\displaystyle K(k)\equiv {\frac {5}{1+2\operatorname {dn} \left[{\tfrac {2}{5}}K(k),k\right]+2\operatorname {dn} \left[{\tfrac {4}{5}}K(k),k\right]}}K\left\{k^{5}\operatorname {sn} \left[{\tfrac {1}{5}}K(k),k\right]^{4}\operatorname {sn} \left[{\tfrac {3}{5}}K(k),k\right]^{4}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/739fe847c7877f62102d1eabc72d8a2de2e7fd6e)
![{\displaystyle K(k)\equiv {\frac {7}{1+2\operatorname {dn} \left[{\tfrac {2}{7}}K(k),k\right]+2\operatorname {dn} \left[{\tfrac {4}{7}}K(k),k\right]+2\operatorname {dn} \left[{\tfrac {6}{7}}K(k),k\right]}}K\left\{k^{7}\operatorname {sn} \left[{\tfrac {1}{7}}K(k),k\right]^{4}\operatorname {sn} \left[{\tfrac {3}{7}}K(k),k\right]^{4}\operatorname {sn} \left[{\tfrac {5}{7}}K(k),k\right]^{4}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2fd46746b30bcca49e2229ec9c6c5aa7d2b829)
![{\displaystyle \operatorname {sn} \left[{\tfrac {1}{3}}K(k),k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7891e0ada3c2a09ae0a28ec09ed7732ed3a75c56)



![{\displaystyle K(k)\equiv {\frac {n}{\sum \limits _{a=1}^{n}\operatorname {dn} \left[{\frac {2a}{n}}K(k),k\right]}}K\left\{k^{n}\prod _{a=1}^{n}\operatorname {sn} \left[{\frac {2a-1}{n}}K(k),k\right]^{2}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76d5dfb460824e9f1031df3e68bff6a4c547b652)





![{\displaystyle E\left(\varphi ,k\right)=\left[1-{\frac {k^{2}}{2}}\left(\sum \limits _{n=0}^{\infty }\prod \limits _{i=1}^{n}{\frac {k_{-i}}{2^{n}}}\right)\right]F\left(\varphi ,k\right)+k\sum \limits _{n=1}^{\infty }{\frac {\sqrt {\prod \limits _{i=1}^{n}k_{-i}}}{2^{n}}}\sin \varphi _{-n}^{L}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dac82d60d172dec5f713d536c1f7f853f62190ee)






![{\displaystyle \forall k^{2}\in ]-\infty ;1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1d2d32b5c6d23dd36e6b13f29277c920c2675df)
![{\displaystyle {\begin{aligned}K(k)&=\int \limits _{\theta =0}^{\pi /2}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}\,\mathrm {d} \theta ={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[P_{2n}\left(0\right)\right]^{2}k^{2n}\\&={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {\operatorname {CBC} \left(n\right)}{2^{2n}}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {C_{2n}^{n}}{2^{2n}}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }\left[{\frac {\left(2n\right)!}{2^{2n}n!^{2}}}\right]^{2}k^{2n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af93c6eaf60a997c6eaa7ee515eea2ebc8c54281)






![{\displaystyle \partial _{k^{i}}^{i}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}={\frac {\sum \limits _{j=0}^{\lfloor {i/2}\rfloor }2^{j}j!\left[C_{\lfloor {i/2}\rfloor }^{j}\right]^{2}\left[\prod \limits _{m=1}^{\lfloor \left(i+1\right)/2\rfloor }(2m-1)^{1+\left[m>j+\left(i-2\lfloor {i/2}\rfloor \right)\right]}\right]k^{2j+\left(i-2\lfloor {i/2}\rfloor \right)}\sin ^{i+2j+\left(i-2\lfloor {i/2}\rfloor \right)}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c58eb20a4c84529c4ef9c59264a0f43c9f9b358)
![{\displaystyle \Leftrightarrow {\begin{cases}i{\text{ pair }}&:\partial _{k^{i}}^{i}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}={\frac {\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\i{\text{ impair }}&:\partial _{k^{i}}^{i}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}={\frac {\sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+1}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8561a55b19059b596ef44d92a637ce4c56d6701c)


![{\displaystyle {\begin{cases}\partial _{k^{0}}^{0}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}&={\frac {\sum \limits _{j=0}^{0}\left[\prod \limits _{m=1}^{0}(2m-1)^{1+\left[m>0\right]}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{1/2}}}\\\partial _{k^{1}}^{1}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}&={\frac {\sum \limits _{j=0}^{0}\left[\prod \limits _{m=1}^{1}(2m-1)^{1+\left[m>1\right]}\right]k\sin ^{2}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{3/2}}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f1c1bb968e6806ac8fea004d89e8faba3ffa91c)


![{\displaystyle {\begin{aligned}\partial _{k^{i+1}}^{i+1}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}&={\frac {\left[{\begin{matrix}\left(1-k^{2}\sin ^{2}\theta \right)\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2j\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j-1}\sin ^{i+2j}\theta \\+\left(2i+1\right)k\sin ^{2}\theta \sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2j\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j-1}\sin ^{i+2j}\theta \\+\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2i-2j+1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j'=j-1=0}^{i/2-1}2^{j'+1}\left(j'+1\right)!\left[C_{i/2}^{j'+1}\right]^{2}\left(2j'+2\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j'+1\right]}\right]k^{2j'+1}\sin ^{i+2j'+2}\theta \\+\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2i-2j+1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2-1}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\left[{\frac {i/2-j}{j+1}}\right]^{2}\left(2j+2\right)^{2}+\left(2i-2j+1\right)\left(2j+1\right)\right]\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \\+\sum \limits _{j=i/2}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(i+1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2-1}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\left(i-2j\right)^{2}+\left(2i-2j+1\right)\left(2j+1\right)\right]\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \\+\sum \limits _{j=i/2}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(i+1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2-1}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(i+1\right)^{2}\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \\+\sum \limits _{j=i/2}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(i+1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\sum \limits _{j=0}^{i/2}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2+1}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e0b1264dbeaae8df077a6d41e2d52099fed42fd)
![{\displaystyle {\begin{aligned}\partial _{k^{i+1}}^{i+1}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}&={\frac {\left[{\begin{matrix}\left(1-k^{2}\sin ^{2}\theta \right)\sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2j+1\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\left(2i+1\right)k\sin ^{2}\theta \sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2j+1\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2i-2j\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+2}\sin ^{i+2j+3}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2j+1\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j'=j+1=1}^{\left(i+1\right)/2}2^{j'-1}\left(j'-1\right)!\left[C_{\left(i-1\right)/2}^{j'-1}\right]^{2}\left(2i-2j'+2\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j'\right]}\right]k^{2j'}\sin ^{i+2j'+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>0\right]}\right]\sin ^{i+1}\theta \\+\sum \limits _{j=1}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}\left[\left[{\frac {\left(i+1\right)/2-j}{\left(i+1\right)/2}}\right]^{2}+\left[{\frac {j}{\left(i+1\right)/2}}\right]^{2}{\frac {1}{2j}}\left(2i-2j+2\right)\right]\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j=\left(i+1\right)/2}^{\left(i+1\right)/2}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}\left[{\frac {j}{\left(i+1\right)/2}}\right]^{2}{\frac {1}{2j}}\left(2i-2j+2\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\left[{\begin{matrix}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>0\right]}\right]\sin ^{i+1}\theta \\+\sum \limits _{j=1}^{\left(i-1\right)/2}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}{\frac {\left(i+1-2j\right)^{2}+2j\left(2i-2j+2\right)}{\left(i+1\right)^{2}}}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j=\left(i+1\right)/2}^{\left(i+1\right)/2}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}{\frac {2j\left(2i-2j+2\right)}{\left(i+1\right)^{2}}}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\\&={\frac {\sum \limits _{j=0}^{\left(i+1\right)/2}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+3\right)/2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e46f67192dea7e8c3b0cf73aeb7622a599a8c78)
![{\displaystyle {\frac {1}{\sqrt {1-k^{2}\sin ^{2}\theta }}}=\sum \limits _{i=0}^{\infty }{\frac {\left[\prod \limits _{m=1}^{i}\left(2m-1\right)^{2}\right]\sin ^{2i}\theta k^{2i}}{\left(2i\right)!}}=\sum \limits _{i=0}^{\infty }{\frac {\left(2i\right)!}{2^{2i}i!^{2}}}k^{2i}\sin ^{2i}\theta =\sum \limits _{i=0}^{\infty }{\frac {C_{2i}^{i}}{2^{2i}}}k^{2i}\sin ^{2i}\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a591185f0377230d7fdbea3000b473a415ecf0c0)
![{\displaystyle \lim \limits _{i\to \infty }{\frac {\left(2i\right)!}{2^{2i}i!^{2}}}=\prod \limits _{i=1}^{\infty }\left(1-{\frac {1}{2i}}\right)=\mathrm {e} ^{\sum \limits _{i=0}^{\infty }\ln \left(1-{\frac {1}{2i}}\right)}=\mathrm {e} ^{\lambda _{i_{0}}+\sum \limits _{i=i_{0}}^{\infty }\ln \left(1-{\frac {1}{2i}}\right)}\sim \mathrm {e} ^{\lambda _{i_{0}}-\sum \limits _{i=i_{0}}^{\infty }{\frac {1}{2i}}}\sim \mathrm {e} ^{\lambda _{i_{0}}-\left[{\frac {\ln {i}}{2}}\right]_{i_{0}}^{\infty }}\sim 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b28d9f73dec8e4c327eecb9de0ee5c766495a47)
![{\displaystyle {\begin{aligned}\int \limits _{\theta =0}^{\pi /2}\sin ^{2n}x\,\mathrm {d} \theta &=\int \limits _{\theta =0}^{\pi /2}\left({\frac {\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}}{2i}}\right)^{2n}\,\mathrm {d} \theta =\int \limits _{\theta =0}^{\pi /2}\sum \limits _{j=0}^{2n}C_{2n}^{j}{\frac {\left(-1\right)^{j}\mathrm {e} ^{\mathrm {i} \left(2n-2j\right)x}}{2^{2n}\left(-1\right)^{n}}}\,\mathrm {d} \theta \\&=\int \limits _{\theta =0}^{\pi /2}{\frac {1}{2^{2n}}}\left[\sum \limits _{j=0}^{n-1}\left(-1\right)^{j}C_{2n}^{j}{\frac {\mathrm {e} ^{\mathrm {i} \left(2n-2j\right)x}+\mathrm {e} ^{-\mathrm {i} \left(2n-2j\right)x}}{\left(-1\right)^{n}}}+C_{2n}^{n}\right]\mathrm {d} \theta \\&=\int \limits _{\theta =0}^{\pi /2}\left[\sum \limits _{j=0}^{n-1}{\frac {\left(-1\right)^{n+j}C_{2n}^{j}\cos \left[\left(2n-2j\right)x\right]}{2^{2n-1}}}+{\frac {C_{2n}^{n}}{2^{2n}}}\right]\mathrm {d} \theta \\&=\left[\sum \limits _{j=0}^{n-1}{\frac {\left(-1\right)^{n+j+1}C_{2n}^{j}\sin \left[\left(2n-2j\right)x\right]}{2^{2n-1}\left(2n-2j\right)}}+{\frac {C_{2n}^{n}}{2^{2n}}}\theta \right]_{\theta =0}^{\pi /2}={\frac {\pi }{2}}{\frac {C_{2n}^{n}}{2^{2n}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e03eced2b8cd49a70fe5cd9c2f47302f82c8f74f)

![{\displaystyle k\in ]0;1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aee3c3fcdebeaa5c3c862d3d254bc04993d74ed5)

![{\displaystyle \forall k^{2}\in ]-\infty ;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/930bd296b84179bf0971a6f0161488e19a6b4fc2)
![{\displaystyle {\begin{aligned}E(k)&=\int \limits _{\theta =0}^{\pi /2}{\sqrt {1-k^{2}\sin ^{2}\theta }}\,\mathrm {d} \theta ={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {1}{1-2n}}\left[P_{2n}\left(0\right)\right]^{2}k^{2n}\\&={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {1}{1-2n}}\left[{\frac {\operatorname {CBC} \left(n\right)}{2^{2n}}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {1}{1-2n}}\left[{\frac {C_{2n}^{n}}{2^{2n}}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {1}{1-2n}}\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}k^{2n}={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {1}{1-2n}}\left[{\frac {\left(2n\right)!}{2^{2n}n!^{2}}}\right]^{2}k^{2n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4029b94253433816d05881063890fb1ff66d67f5)

![{\displaystyle \partial _{k^{i}}^{i}{\sqrt {1-k^{2}\sin ^{2}\theta }}={\frac {\sum \limits _{j=0}^{\lfloor {i/2}\rfloor }-{\frac {\lfloor {i/2}\rfloor -j}{\lfloor {i/2}\rfloor \left[i-1+\left(i-2\lfloor {i/2}\rfloor \right)\right]}}2^{j}j!\left[C_{\lfloor {i/2}\rfloor }^{j}\right]^{2}\left[\prod \limits _{m=1}^{\lfloor \left(i+1\right)/2\rfloor }(2m-1)^{1+\left[m>j+\left(i-2\lfloor {i/2}\rfloor \right)\right]}\right]k^{2j+\left(i-2\lfloor {i/2}\rfloor \right)}\sin ^{i+2j+\left(i-2\lfloor {i/2}\rfloor \right)}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i-1\right)/2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1abfe417ceb04c19bc680747964bc482eea30d62)
![{\displaystyle \Leftrightarrow {\begin{cases}i{\text{ pair }}&:\partial _{k^{i}}^{i}{\sqrt {1-k^{2}\sin ^{2}\theta }}={\frac {\sum \limits _{j=0}^{i/2}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i-1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i-1\right)/2}}}\\i{\text{ impair }}&:\partial _{k^{i}}^{i}{\sqrt {1-k^{2}\sin ^{2}\theta }}={\frac {\sum \limits _{j=0}^{\left(i-1\right)/2}-{\frac {{\frac {i-1}{2}}-j}{{\frac {i-1}{2}}i}}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+1}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i-1\right)/2}}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/045cf8c7a9f3e4b5556606c6082ba446c49cb5b7)



![{\displaystyle {\begin{aligned}\partial _{k^{i+1}}^{i+1}{\sqrt {1-k^{2}\sin ^{2}\theta }}&={\frac {\left[{\begin{matrix}\left(1-k^{2}\sin ^{2}\theta \right)\sum \limits _{j=0}^{i/2}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i-1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2j\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j-1}\sin ^{i+2j}\theta \\+\left(2i-1\right)k\sin ^{2}\theta \sum \limits _{j=0}^{i/2}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i-1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i-1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2j\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j-1}\sin ^{i+2j}\theta \\+\left(2i-2j-1\right)\sum \limits _{j=0}^{i/2}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i-1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j'=j-1=0}^{i/2-1}-{\frac {{\frac {i}{2}}-j'-1}{{\frac {i}{2}}\left(i-1\right)}}2^{j'+1}\left(j'+1\right)!\left[C_{i/2}^{j'+1}\right]^{2}\left(2j'+2\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j'+1\right]}\right]k^{2j'+1}\sin ^{i+2j'+2}\theta \\+\left(2i-2j-1\right)\sum \limits _{j=0}^{i/2}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i-1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2-1}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i-1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[{\frac {{\frac {i}{2}}-j-1}{{\frac {i}{2}}-j}}\left[{\frac {i/2-j}{j+1}}\right]^{2}4\left(j+1\right)^{2}+\left(2i-2j-1\right)\left(2j+1\right)\right]\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \\+\sum \limits _{j=i/2}^{i/2}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i-1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(2i-2j-1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{i/2-1}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i-1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(i^{2}-1\right])\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \\+\sum \limits _{j=i/2}^{i/2}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i-1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left(i-1\right)\left[\prod \limits _{m=1}^{i/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\&={\frac {\sum \limits _{j=0}^{i/2}-{\frac {{\frac {i}{2}}-j}{{\frac {i}{2}}\left(i+1\right)}}2^{j}j!\left[C_{i/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{i/2+1}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+2}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/347deccbe1b485b31e2ab199f03262d73401feec)
![{\displaystyle {\begin{aligned}\partial _{k^{i+1}}^{i+1}{\sqrt {1-k^{2}\sin ^{2}\theta }}&={\frac {\left[{\begin{matrix}\left(1-k^{2}\sin ^{2}\theta \right)\sum \limits _{j=0}^{\left(i-1\right)/2}-{\frac {{\frac {i-1}{2}}-j}{{\frac {i-1}{2}}i}}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2j+1\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\left(2i-1\right)k\sin ^{2}\theta \sum \limits _{j=0}^{\left(i-1\right)/2}-{\frac {{\frac {i-1}{2}}-j}{{\frac {i-1}{2}}i}}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+1}\sin ^{i+2j+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{\left(i-1\right)/2}-{\frac {{\frac {i-1}{2}}-j}{{\frac {i-1}{2}}i}}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2j+1\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j=0}^{\left(i-1\right)/2}-{\frac {{\frac {i-1}{2}}-j}{{\frac {i-1}{2}}i}}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2i-2j-2\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j+2}\sin ^{i+2j+3}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{\left(i-1\right)/2}-{\frac {{\frac {i-1}{2}}-j}{{\frac {i-1}{2}}i}}2^{j}j!\left[C_{\left(i-1\right)/2}^{j}\right]^{2}\left(2j+1\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j+1\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j'=j+1=1}^{\left(i+1\right)/2}-{\frac {{\frac {i-1}{2}}-j'+1}{{\frac {i-1}{2}}i}}2^{j'-1}\left(j'-1\right)!\left[C_{\left(i-1\right)/2}^{j'-1}\right]^{2}\left(2i-2j'\right)\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j'\right]}\right]k^{2j'}\sin ^{i+2j'+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{\left(i-1\right)/2}-{\frac {{\frac {i+1}{2}}-j}{{\frac {i+1}{2}}i}}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}\left[{\frac {\left(i+1\right)/2-j}{\left(i+1\right)/2}}\right]^{2}{\frac {{\frac {i+1}{2}}i}{{\frac {i+1}{2}}-j}}{\frac {{\frac {i-1}{2}}-j}{{\frac {i-1}{2}}i}}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j=1}^{\left(i+1\right)/2}-{\frac {{\frac {i+1}{2}}-j}{{\frac {i+1}{2}}i}}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}\left[{\frac {j}{\left(i+1\right)/2}}\right]^{2}{\frac {{\frac {i+1}{2}}i}{{\frac {i+1}{2}}-j}}{\frac {{\frac {i-1}{2}}-j+1}{{\frac {i-1}{2}}i}}{\frac {i-j}{j}}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\&={\frac {\left[{\begin{matrix}\sum \limits _{j=0}^{\left(i-1\right)/2}-{\frac {{\frac {i+1}{2}}-j}{{\frac {i+1}{2}}i}}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}{\frac {\left(i-2j+1\right)\left(i-2j-1\right)}{i^{2}-1}}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \\+\sum \limits _{j=1}^{\left(i+1\right)/2}-{\frac {{\frac {i+1}{2}}-j}{{\frac {i+1}{2}}i}}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}{\frac {4j\left(i-j\right)}{i^{2}-1}}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta \end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\\&={\frac {\sum \limits _{j=0}^{\left(i+1\right)/2}-{\frac {{\frac {i+1}{2}}-j}{{\frac {i+1}{2}}i}}2^{j}j!\left[C_{\left(i+1\right)/2}^{j}\right]^{2}\left[\prod \limits _{m=1}^{\left(i+1\right)/2}(2m-1)^{1+\left[m>j\right]}\right]k^{2j}\sin ^{i+2j+1}\theta }{\left(1-k^{2}\sin ^{2}\theta \right)^{\left(2i+1\right)/2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eece720600cc9130d8ad1c9be098230c19b7a4f)
![{\displaystyle {\sqrt {1-k^{2}\sin ^{2}\theta }}=1+\sum \limits _{i=1}^{\infty }{\frac {\left[\prod \limits _{m=1}^{i}\left(2m-1\right)^{2}\right]\sin ^{2i}\theta k^{2i}}{\left(1-2i\right)\left(2i\right)!}}=\sum \limits _{i=0}^{\infty }{\frac {\left(2i\right)!}{\left(1-2i\right)2^{2i}i!^{2}}}k^{2i}\sin ^{2i}\theta =\sum \limits _{i=0}^{\infty }{\frac {C_{2i}^{i}}{\left(1-2i\right)2^{2i}}}k^{2i}\sin ^{2i}\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3c51d0633d9a4a20499158897593a6bd99c694a)





![{\displaystyle {\begin{aligned}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}&={\frac {\partial _{\varphi _{2}}\left[\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right)\right]}{\sqrt {1-k^{2}\sin ^{2}\left[\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right]\right)}}}\\&={\frac {{\frac {-k^{2}\tan \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}}{\left[1+\tan ^{2}\varphi _{1}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)\right]{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}+{\frac {\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\left[1+\tan ^{2}\varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{1}\right)\right]\cos ^{2}\varphi _{2}}}}{\sqrt {1-k^{2}\left[{\frac {\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}+\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}}{{\sqrt {1+\tan ^{2}\varphi _{1}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)}}{\sqrt {1+\tan ^{2}\varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{1}\right)}}}}\right]^{2}}}}\\&={\frac {\frac {-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right){\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}{\sqrt {1-k^{2}\left[{\frac {\cos \varphi _{2}\sin \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}+\cos \varphi _{1}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}}{1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}}}\right]^{2}}}}\\&={\frac {\frac {-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{\sqrt {\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)^{2}-k^{2}\cos ^{2}\varphi _{2}\sin ^{2}\varphi _{1}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)-k^{2}\cos ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{1}\right)-2k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}\\&={\frac {\frac {-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{\sqrt {1-k^{2}\left(\sin ^{2}\varphi _{1}+\sin ^{2}\varphi _{2}\right)+k^{4}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\left(\cos ^{2}\varphi _{1}+\cos ^{2}\varphi _{2}+\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)-2k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}\\&={\frac {1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/325d57c930f9b85d5b646fa60d19fb1ea861f28d)

![{\displaystyle \arcsin x\in [-\pi /2;\pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fa963030febe25f645f01f1332ef5bf06ccae9e)
![{\displaystyle \arccos x\in [0;\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11b04ee9722b92bc6ef380b7bd62d2eebfb402de)

![{\displaystyle \textstyle E\left(\varphi _{1},k\right)+E\left(\varphi _{2},k\right)=\left[{\begin{aligned}E\left(\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right),k\right)\\+{\frac {k^{2}\sin \varphi _{1}\sin \varphi _{2}\left(\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}\right)}{1-k^{2}\sin \varphi _{1}\sin \varphi _{2}}}\end{aligned}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b42b85802f1d5c5d1662a33f4d575098caf657bd)
![{\displaystyle \textstyle {\begin{aligned}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}&={\frac {\left[{\begin{matrix}\left(-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)^{2}\\+k^{2}\sin \varphi _{1}\left[{\begin{matrix}\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)\\\times \left[{\begin{matrix}\cos \varphi _{2}\left[\sin \varphi _{1}\cos \varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)+\cos \varphi _{1}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right]\\+\sin \varphi _{2}\left[{\begin{matrix}-\sin \varphi _{1}\sin \varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)-k^{2}\sin \varphi _{1}\cos ^{2}\varphi _{2}\sin \varphi _{2}\\+\cos \varphi _{1}\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\end{matrix}}\right]\end{matrix}}\right]\\+2k^{2}\sin ^{2}\varphi _{1}\cos \varphi _{2}\sin ^{2}\varphi _{2}\left[\sin \varphi _{1}\cos \varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)+\cos \varphi _{1}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right]\end{matrix}}\right]\end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)^{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\frac {\left[{\begin{matrix}\left(-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)^{2}\\+k^{2}\sin \varphi _{1}\left[{\begin{matrix}\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)\\\times \left[{\begin{matrix}\sin \varphi _{1}\left(\cos ^{2}\varphi _{2}-\sin ^{2}\varphi _{2}\right)-k^{2}\sin \varphi _{1}\sin ^{2}\varphi _{2}\left(2\cos ^{2}\varphi _{2}-\sin ^{2}\varphi _{2}\right)\\+2\cos \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\end{matrix}}\right]\\+2k^{2}\sin ^{2}\varphi _{1}\cos \varphi _{2}\sin ^{2}\varphi _{2}\left[\sin \varphi _{1}\cos \varphi _{2}\left(1-k^{2}\sin ^{2}\varphi _{2}\right)+\cos \varphi _{1}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right]\end{matrix}}\right]\end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)^{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\frac {\left[{\begin{matrix}\left(-k^{2}\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}+{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)^{2}\\+k^{2}\sin \varphi _{1}\left[{\begin{matrix}\sin \varphi _{1}\left(\cos ^{2}\varphi _{2}-\sin ^{2}\varphi _{2}\right)\\+k^{2}\left[\sin \varphi _{1}\sin ^{2}\varphi _{2}\left(\sin ^{2}\varphi _{1}-2\cos ^{2}\varphi _{2}+\sin ^{2}\varphi _{2}\right)\right]\\-k^{4}\sin ^{3}\varphi _{1}\sin ^{6}\varphi _{2}\\+2\cos \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\end{matrix}}\right]\end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)^{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\frac {\left[{\begin{matrix}k^{4}\cos ^{2}\varphi _{1}\sin ^{2}\varphi _{1}\cos ^{2}\varphi _{2}\sin ^{2}\varphi _{2}+\left(1-k^{2}\sin ^{2}\varphi _{1}\right)\left(1-k^{2}\sin ^{2}\varphi _{2}\right)\\+k^{2}\sin ^{2}\varphi _{1}\left(\cos ^{2}\varphi _{2}-\sin ^{2}\varphi _{2}\right)\\+k^{4}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\left(\sin ^{2}\varphi _{1}-2\cos ^{2}\varphi _{2}+\sin ^{2}\varphi _{2}\right)\\-k^{6}\sin ^{4}\varphi _{1}\sin ^{6}\varphi _{2}\end{matrix}}\right]}{\left(1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)^{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\frac {\left[{\begin{matrix}1+k^{2}\sin ^{2}\varphi _{2}\left(-2\sin ^{2}\varphi _{1}-1\right)\\+k^{4}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\left(\sin ^{2}\varphi _{1}-\cos ^{2}\varphi _{2}+2\sin ^{2}\varphi _{2}+1-\sin ^{2}\varphi _{1}-\sin ^{2}\varphi _{2}+\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}\right)\\-k^{6}\sin ^{4}\varphi _{1}\sin ^{6}\varphi _{2}\end{matrix}}\right]}{\left(1-2k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}+k^{4}\sin ^{4}\varphi _{1}\sin ^{4}\varphi _{2}\right){\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\frac {1+k^{2}\sin ^{2}\varphi _{2}\left(-2\sin ^{2}\varphi _{1}-1\right)+k^{4}\sin ^{2}\varphi _{1}\sin ^{4}\varphi _{2}\left(2+\sin ^{2}\varphi _{1}\right)-k^{6}\sin ^{4}\varphi _{1}\sin ^{6}\varphi _{2}}{\left(1-2k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}+k^{4}\sin ^{4}\varphi _{1}\sin ^{4}\varphi _{2}\right){\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}}\\&={\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f8c055f91f66e4a8e5713cb82fa149552e51daf)
![{\displaystyle \textstyle {\begin{aligned}E\left(\varphi _{1},k\right)+E\left(\varphi _{2},k\right)&=\left[{\begin{aligned}E\left(\arctan \left(\tan \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\right)+\arctan \left(\tan \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\right),k\right)\\+{\frac {k^{2}\sin \varphi _{1}\sin \varphi _{2}\left(\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}\right)}{1-k^{2}\sin \varphi _{1}\sin \varphi _{2}}}\end{aligned}}\right]\\&=\left[{\begin{aligned}E\left(\arcsin {\frac {\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}}{1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}}},k\right)\\+{\frac {k^{2}\sin \varphi _{1}\sin \varphi _{2}\left(\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}\right)}{1-k^{2}\sin \varphi _{1}\sin \varphi _{2}}}\end{aligned}}\right]\\&=\left[{\begin{aligned}E\left(\arccos {\frac {1-\cos \varphi _{1}\sin \varphi _{1}\cos \varphi _{2}\sin \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}}{1-k^{2}\sin ^{2}\varphi _{1}\sin ^{2}\varphi _{2}}},k\right)\\+{\frac {k^{2}\sin \varphi _{1}\sin \varphi _{2}\left(\cos \varphi _{1}{\sqrt {1-k^{2}\sin ^{2}\varphi _{1}}}\sin \varphi _{2}+\cos \varphi _{2}{\sqrt {1-k^{2}\sin ^{2}\varphi _{2}}}\sin \varphi _{1}\right)}{1-k^{2}\sin \varphi _{1}\sin \varphi _{2}}}\end{aligned}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1ba66043c07fdfca615e301d9f0dac0f2db2f64)