Effet Tcherenkov

L'effet Tcherenkov, parfois nommé effet Vavilov-Tcherenkov, est un phénomène similaire à une onde de choc, produisant un flash de lumière lorsqu'une particule chargée se déplace dans un milieu diélectrique avec une vitesse supérieure à la vitesse de la lumière dans ce milieu (la vitesse de la lumière dans le vide étant toujours supérieure à celle de la particule)[1].
Cet effet provoque par exemple la luminosité bleutée de l'eau entourant le cœur d'un réacteur nucléaire.
Terminologie
[modifier | modifier le code]L'effet Vavilov-Tcherenkov porte le nom des physiciens russes Sergueï Vavilov et Pavel Tcherenkov. Il est souvent nommé simplement effet Tcherenkov, les travaux ayant été publiés sous le nom de Pavel Tcherenkov uniquement, et orthographié Tcherenkov (à la française)[2], Cherenkov (à l'anglaise) ou encore « Čerenkov ». On rencontre également plus rarement l'appellation effet Mallet-Tcherenkov ou Tcherenkov-Mallet, particulièrement en radioprotection en France, le Français Lucien Mallet étant le premier à avoir travaillé sur le sujet — et contraint d'abandonner ses travaux faute de financement.
Historique
[modifier | modifier le code]L’effet Tcherenkov était connu depuis 1910 et les travaux de Marie Curie montrant que l'eau soumise à une source radioactive produisait de la lumière. Jusqu'en 1926, l'explication admise était la fluorescence produite par des solutés. Mais entre 1926 et 1929, Lucien Mallet analysa plus profondément la question et remarqua que le spectre lumineux produit était continu, alors que la fluorescence donne un spectre discontinu.
Pour des besoins de recherche en astrophysique, T.S. van Albada et J. Borgman construisirent une source étalon basée sur cet effet, sans toutefois en déterminer quantitativement le rayonnement[3]. En effet, les recherches en astronomie ultra-violette débutèrent dès le début des années 1960, aussi bien aux États-Unis (avec Riccardo Giacconi) qu'en France, grâce aux développements rapides des fusées et lanceurs (Aerobee, Diamant, etc.) qui permirent d'atteindre les couches supérieures de l'atmosphère terrestre, encore que pour des temps d'exposition très courts. L'objectif étant notamment de s'affranchir de la couche d'ozone autour de 40 km d'altitude, qui filtre le spectre UV, riche d'informations, de la lumière émise par les objets célestes. En 1973, une source à effet Tcherenkov à base de strontium 90 fut réalisée et étudiée par Chon Trung Hua, chercheur au Laboratoire d'astronomie spatiale (L.A.S.), afin de pouvoir étalonner photométriquement en vol ces observations ultra-violettes (de longueur d'onde < 3000 Å, donc extra-atmosphériques) des sources célestes par les caméras embarquées mises au point par ce même laboratoire du CNRS. Une telle source étalon, autonome et particulièrement compacte, était facile à fixer à bord des fusées car elle ne nécessitait pas d'alimentation électrique externe. La distribution spectrale d'énergie du spectre continu fut ainsi mesurée pour la première fois, par comparaison avec le rayonnement de corps noir via des sources étalons secondaires[4].
En outre, entre 1934 et 1937, Pavel Tcherenkov a prouvé que la radiation produite est indépendante de la composition du liquide, ce qui était en désaccord avec la théorie de la fluorescence.
Les recherches de Tcherenkov établissaient les propriétés générales de la radiation, mais ce sont Ilia Frank et Igor Tamm qui décrivirent cet effet de façon rigoureuse, en 1937, ce qui leur valut de partager avec Tcherenkov le prix Nobel de physique de 1958.
L’effet Tcherenkov joue un rôle capital dans la physique actuelle. Il intervient dans la détection des particules (à l'observatoire de neutrinos de Sudbury, à l'Antarctic Muon and Neutrino Detector Array, au Super-Kamiokande) ou encore dans les accélérateurs de particules. Cette méthode est particulièrement simple et requiert très peu d’informations pour pouvoir déduire la masse et la vitesse d’une particule. C’est pourquoi on la retrouve dans toutes les installations de physique subatomique.
L’effet Tcherenkov est également utilisé pour la détection de rayons cosmiques de très haute énergie : voir l'article Very Energetic Radiation Imaging Telescope Array System.
Explication du phénomène
[modifier | modifier le code]
Dans un milieu matériel, la lumière se déplace à une vitesse , où est la vitesse de la lumière dans le vide et est l'indice de réfraction du milieu. Une particule chargée peut se déplacer dans ce milieu à une vitesse v supérieure à c1 mais inférieure à c, ce qui ne contredit pas la théorie de la relativité[1]. La particule chargée interagit, tout au long de sa trajectoire, avec le milieu qu'elle traverse en perturbant temporairement la polarisation des couches électroniques des atomes rencontrés, ce qui provoque une émission radiative. Chaque atome rencontré par la particule devient donc émetteur d'un rayonnement à son passage. Or l'onde émise se propage à la vitesse c1 inférieure à v. L'interférence des ondes émises par chaque atome perturbé est alors constructive ; un front d'onde cohérent apparaît sous la forme d'un cône de lumière. La fréquence de cette onde constructive correspond généralement, pour l'effet Tcherenkov dans l'eau, à celle du bleu ou de l'ultraviolet.
L’analogie entre l’effet Tcherenkov et l'onde de choc est facile à faire. Un avion se déplaçant plus vite que le son dans l’air crée une onde de choc sur laquelle toutes les ondes sonores se retrouvent. La correspondance avec l’effet Tcherenkov se fait en remplaçant l’avion assimilé à un point par une particule chargée et le son par la lumière. L'étude du nombre de Mach fournit un cadre de pensée qui est directement applicable ici.
Explication de l'ouverture angulaire du phénomène
[modifier | modifier le code]Le rayonnement de la particule est émis dans un cône centré sur la trajectoire et caractérisé par son ouverture angulaire
avec :
Deux démonstrations de cette formule sont possibles. Pour chacune d'elles, on utilisera les hypothèses suivantes :
- la particule se déplace toujours dans la même direction (pas de diffusion sur les molécules du milieu) et à vitesse v constante (on ne prend pas en compte la perte d'énergie par rayonnement) ;
- on considère le rayonnement d'une longueur de la trajectoire de la particule, où est la longueur d'onde du rayonnement émis ;
- on considère l'onde émise en chaque point comme une onde sphérique de pulsation . On pourra éventuellement se ramener à des ondes plus complexes par transformation de Fourier grâce à la linéarité des équations de Maxwell ;
- on ne tient pas compte de la diminution d'amplitude due à la distance ;
- chaque point commence à rayonner avec une phase nulle au moment où l'électron passe en ce point.
Première démonstration
[modifier | modifier le code]
On se place dans les conditions de Fraunhofer (l'observateur M est situé à l'infini) pour déterminer l'amplitude rayonnée dans la direction . Pour ce faire, il nous faut additionner les contributions de chaque point P de la trajectoire.
Prenons un point O de référence au centre de la trace. Quitte à changer l'origine des temps, on peut considérer que l'élément de trace autour de O commence à rayonner à l'instant donc qu'il émet une onde
.
Sa contribution au point M s'écrit donc
.
On ne tient pas compte de la diminution d'amplitude due à la propagation des ondes sphériques, car dans les conditions de Fraunhoffer le point M est situé à une distance de la trajectoire et la diminution est la même pour chaque point émetteur.
L'élément de trajectoire situé au point P, à une distance x du point O, commence à rayonner à l'instant
.
Il émet donc une onde dont l'amplitude est
et sa contribution au point M peut s'écrire
.
En sommant toutes les contributions et en utilisant la loi du retour inverse et le théorème de Malus pour déterminer la différence de marche entre les différents chemins, on obtient l'amplitude rayonnée dans la direction :
où représente la différence de marche .
On en déduit
où . En considérant l'intensité comme la valeur moyenne temporelle du carré du module de l'amplitude sur un grand nombre de période et en notant l'intensité émise par l'ensemble de la trajectoire, on trouve
Avec , la fonction est assimilable à la fonction de Dirac . Dans cette limite, on obtient la condition Tcherenkov :
Seconde démonstration
[modifier | modifier le code]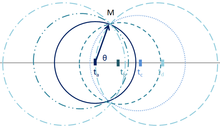
On peut mener un second type de raisonnement, plus qualitatif, pour comprendre la valeur de l'angle d'ouverture du cône de rayonnement. Ce raisonnement s'appuie sur les arguments développés par Richard Feynman dans son livre Lumière et Matière[5].
En tout point M de l'espace se superposent les ondes issues de chaque point de la trace. Toutes ces ondes présentent des phases différentes, qui dépendent à la fois de leur instant d'émission et de leur propagation jusqu'au point M. Pour chacun de ces points on peut trouver un point x qui fournit un signal en opposition de phase au premier, tant et si bien que leur somme s'annule. Il existe pourtant un point tel que les contributions de tous les points autour de ont la même phase et s'additionnent constructivement. Ce point est caractérisé par . Or, en prenant l'origine des phases à l'aplomb du point M (comme sur la figure ci-contre), on a
La condition se traduit alors par
Spectre du rayonnement Tcherenkov
[modifier | modifier le code]Le spectre rayonné par la particule chargée lors de son mouvement a été déterminé pour la première fois par Ilia Frank et Igor Tamm en 1937. Il leur a valu, avec Pavel Tcherenkov, le prix Nobel en 1958 pour la découverte et l'interprétation de l'effet Tcherenkov[6]. La formule de Frank-Tamm donne l'énergie rayonnée par une longueur de trace entre et :
.
La courbe de répartition d'énergie a été mesurée pour la première fois (détermination en valeurs absolues et le spectre photographié) entre 2 000 Å et 5 000 Å, par comparaison avec un corps noir[7].
Effet Tcherenkov dans l'espace
[modifier | modifier le code]Les phosphènes des astronautes dans l'espace sont dus à l'effet Tcherenkov[8].
Les astronautes des missions Apollo s'étaient tous plaints de phosphènes lors de leurs missions. On découvrit que ces troubles visuels lumineux étaient dus à l'effet Tcherenkov de particules du vent solaire traversant le liquide des globes oculaires des astronautes.
Dans son livre Sonate au clair de terre, le spationaute français Jean-Loup Chrétien indique que de tels phosphènes se produisent aussi sur Terre, au rythme d'un ou deux en moyenne par personne et par an. Jean-Loup Chrétien rapporte en avoir vu quelques-uns par jour lors de ses séjours à bord de la station Mir.
Notes et références
[modifier | modifier le code]- Gabrielle Bonnet et Mathilde Glénat, « Plus vite que la lumière : effet Cherenkov », Culture Sciences Physique, (lire en ligne, consulté le ).
- « La lumière bleue de l’effet Tcherenkov », sur cea.fr (consulté le )
- A Standard Light-Source for Photoelectric Photometry Based on Cerenkov Radiation, Astrophysical Journal, vol. 132, p.511.
- Hua, Astron. Astrophys., vol. 27, p. 255, 1973.
- R. Feynman, Lumière et matière, Éditions Seuil, (ISBN 2020147580), chapitre 3.
- (en) « The Nobel Prize in Physics 1958 », sur NobelPrize.org (consulté le ).
- Thèse de Doctorat d'état de Hua C.T., 1974, Université d'Aix-Marseille, AO9501.
- (en) L. S. Pinsky, W. Z. Osborne, J. V. Bailey, R. E. Benson et L. F. Thompson, « Light Flashes Observed by Astronauts on Apollo 11 through Apollo 17 » [« Des flash lumineux observés par des astronautes des missions Apollo 11 à 17 »], Science, vol. 183, no 4128, , p. 957-959 (PMID 17756755, DOI 10.1126/science.183.4128.957, lire en ligne).














![{\displaystyle \mathrm {d} s(O,M,t)=s_{0}\mathrm {d} x\,e^{-i\omega t}e^{i{\frac {2\pi }{\lambda }}\left[OM\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbe1e8922f9331abb90159e2cae4d4a0fbd1bcdb)



![{\displaystyle \mathrm {d} s(P,M,t)=s_{0}\mathrm {d} x\,e^{-i\omega \left(t-{\frac {x}{v}}\right)}e^{i{\frac {2\pi }{\lambda }}[PM]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e4017dd59800caa0bbea50c8190913d80b9f8d5)
![{\displaystyle S(\theta )=\int _{-L/2}^{L/2}s_{0}\mathrm {d} x\,e^{-i\omega \left(t-{\frac {x}{v}}\right)}e^{i{\frac {2\pi }{\lambda }}[PM]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06e0932ea8606f6461b3d15704466fa4f321fea0)
![{\displaystyle =s_{0}e^{-i\omega t}e^{i{\frac {2\pi }{\lambda }}[OM]}\int _{-L/2}^{L/2}dx\,e^{i{\frac {2\pi c}{\lambda }}{\frac {x}{v}}}e^{-i{\frac {2\pi }{\lambda }}\delta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/253edff42a6eed74e373585d61318f596e34c94b)

![{\displaystyle \delta =[OM]-[PM]=[OP']=n\,x\,\cos \theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cdf8abdb80739c9adf1bebb65bf8910a187add8)
![{\displaystyle S(\theta )=s_{0}e^{-i\omega t}e^{i{\frac {2\pi }{\lambda }}[OM]}\int _{-L/2}^{L/2}dx\,e^{-i{\frac {2\pi }{\lambda }}\left(n\cos \theta -{\frac {c}{v}}\right)x}=s_{0}{\frac {L}{2}}e^{-i\omega t}e^{i{\frac {2\pi }{\lambda }}[OM]}{\text{sinc}}\left({\frac {\pi L}{\lambda }}\left(n\cos \theta -{\frac {c}{v}}\right)\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2bb41f5c3e14060db19343685be186f136251f9)















