Courant triphasé

Un système de courant (ou tension) triphasé est constitué de trois courants (ou tensions) sinusoïdaux de même fréquence et de même amplitude qui sont déphasés entre eux d'un tiers de tour soit 2π⁄3 radians (ou 120 degrés) dans le cas idéal. Si la fréquence est de 50 Hz, alors les trois phases sont retardées l'une par rapport à l'autre de 1⁄150 seconde (soit 6,7 ms). Lorsque les trois conducteurs sont parcourus par des courants de même valeur efficace et sont déphasés de 2π⁄3, le système est dit équilibré.
Dans le cas de la distribution électrique, le réseau peut se modéliser par trois sources de tension sinusoïdales d'amplitude identique, par exemple 230 V efficaces dans la plupart des pays européens, présentant un angle de phase de 120° entre elles. Idéalement la tension des trois phases est constante et indépendante de la charge, seul le courant de chaque phase devant être dépendant de la puissance de sortie.
Du fait du déphasage de 120°, un réseau dont la tension efficace entre phase et neutre est de 230 V aura une tension composée de efficaces entre phases.
Déroulement historique
[modifier | modifier le code]Les technologies antérieures à l’invention du courant triphasé
[modifier | modifier le code]Plusieurs systèmes électriques différents se sont développés et ont cohabité dans la période de 20 ans précédant l’invention et l’utilisation du courant triphasé, soit pendant les années de 1871 à 1891 dans les pays industrialisés, et principalement en Europe et en Amérique du Nord.
Courant Continu Basse-Tension
[modifier | modifier le code]Le courant continu permettait de transporter l’énergie mais uniquement sur de courtes distances du fait de pertes importantes dans les lignes.
Courant Alternatif Basse-Tension
[modifier | modifier le code]À la même époque, la technologie de courant alternatif est apparue, mais son utilité était très restreinte (alimentation de lampe à arc).
Ces deux systèmes basse-tension, ne convenaient pas pour le transport et la distribution d’électricité, et impliquaient donc que les sources de production soient géographiquement proches des points de consommation.
Pour contrer ce problème, certains ingénieurs ont développé des dynamos à courant continu haute-tension, qui permettaient le transport sur de longues distances. Néanmoins les équipements nécessaires à la conversion vers la basse tension étaient complexes et onéreux ce qui en a limité le développement.
Courant alternatif haute-tension monophasé
[modifier | modifier le code]L’invention du transformateur en courant alternatif a permis l’utilisation du courant haute-tension monophasé.
La différence avec le système précédent est que le transformateur est un équipement peu cher et moins complexe pour la conversion en basse tension.
Tous ces systèmes existants avant le courant triphasé ont assuré certaines des quatre fonctions nécessaires que sont la force motrice, l’éclairage, la distribution et le transport, sans jamais assurer les quatre[1].
Les inventeurs
[modifier | modifier le code]Après la guerre des courants entre Edison et Tesla dans les années 1880 aux États-Unis, le courant alternatif s’impose comme la technologie privilégiée pour le transport de l’électricité.
Ainsi, à partir des années 1880, la deuxième révolution industrielle va être soutenue par l’apparition de nouvelles sources d’énergie dont notamment l’électricité. En effet les usines ont besoin d’énergie en grande quantité, et peuvent êtres éloignées des lieux de production d’électricité. Le développement de technologies permettant de mettre en place un réseau de transport de longue distance de l’électricité permettait ainsi une liberté plus grande quant à l’emplacement de ces usines[2].
C’est dans ce contexte que la technologie du courant alternatif triphasé a été mise au point à travers de multiples expériences et inventions.
Les systèmes d'alimentation comportant plusieurs phases ont été inventés indépendamment par plusieurs ingénieurs dans plusieurs pays différents à la fin des années 1880.
L'alimentation triphasée a évolué à partir du développement des moteurs électriques. En 1885, Galileo Ferraris, à travers ses recherches sur les moteurs électriques, développe l’alternateur permettant de convertir l’énergie mécanique en énergie électrique et fournissant du courant alternatif.
En 1888, Nikola Tesla obtient un brevet pour la conception d'un moteur électrique triphasé.
Mikhail Dolivo-Dobrovolsky a développé un générateur électrique triphasé et un moteur électrique triphasé en 1888 et a étudié les connexions en étoile et en triangle. Son système de transmission triphasé à trois fils a été présenté en Europe lors de l'exposition internationale d'électrotechnique de 1891.
En 1891, Dolivo-Dobrovolsky a utilisé un système de transmission triphasé à trois fils pour transmettre de l'énergie électrique sur une distance de 176 km avec un rendement de 75 %. La même année, il a également créé un transformateur triphasé. Il a conçu la première centrale hydroélectrique triphasée au monde en 1891.
En 1892, la société AEG, et Oskar von Miller réalisent une première ligne de transport de courant en triphasé de 177 km entre Lauffen et Francfort, en Allemagne[3].
Il apparaît donc que le courant triphasé comble les manques des systèmes antérieurs, notamment pour le transport de l’électricité sur de longues distance. La possibilité de transporter l’électricité sur de longues distances va entrainer l’apparition du concept d’interconnexion électrique à grande échelle.
Avantage par rapport au courant monophasé
[modifier | modifier le code]Le courant triphasé permet d'éviter les problèmes de puissance inhérents au courant monophasé alternatif (en régime sinusoïdal). On peut démontrer que le courant triphasé délivre une puissance instantanée sans composante pulsée contrairement au courant monophasé où la puissance instantanée présente une variation sinusoïdale de fréquence double superposée à une composante continue[4]. Il est absolument nécessaire d’annuler cette pulsation de la puissance car elle se retrouve également dans la puissance mécanique transmise par l'arbre de l'alternateur et se traduit par une pulsation du couple mécanique qui peut entraîner la destruction de ce dernier. De plus, les alternateurs triphasés ont un meilleur rendement que leurs homologues monophasés et le régime triphasé occasionne moins de pertes lors du transport en ligne de l'électricité.
L’électrification et l’interconnexion en France et en Europe
[modifier | modifier le code]La capacité du courant triphasé à transporter l’électricité sur de longues distance a favorisé l’électrification des territoires au travers d’interconnexions.
L’interconnexion désigne l’échange d’électricité entre différents réseaux électriques.
Acteurs au niveau local, régional et national
[modifier | modifier le code]L’électrification et l’interconnexion des réseaux électriques se sont faites par étapes. Différents acteurs sont intervenus en fonction de l’ampleur géographique des réseaux.
Au niveau local ce sont les municipalités, ou départements pour le secteur public, mais également des entreprises qui ont permis le développement du réseau électrique.
Pour des zones géographiques de taille supérieure, ce sont les provinces, les Landers, ou encore les cantons, ainsi que des groupes industriels qui interviennent pour l’électrification
Enfin, dès que le niveau national a été atteint, les États, ou encore les groupes industriels deviennent des acteurs principaux pour l’électrification et l’interconnexion des réseaux de niveaux inférieurs.
Ainsi les acteurs du secteur public, aussi bien au niveau local que régional, ou national, interviennent dans l’électrification des territoires.
Leurs interventions peuvent êtres légales, en créant des lois ou des normes. Ainsi la première mission de ces acteurs a été de donner une existence légale à l’électricité, et aux éléments qui contribuent à sa production, sa distribution, et son utilisation, mais également donner un statut aux acteurs publics ou privés qui développent les réseaux électriques ou la production d’électricité. Vient ensuite une phase de réglementation : il devient en effet nécessaire d’encadrer les pratiques afin d’uniformiser le développement de la technologie, et de pouvoir la contrôler. Cela peut passer par la mise en place de normes pour le matériel, ou pour la construction, mais également de concessions, et de réglementations sur le cheminement des câbles sur les territoires. Cet aspect est important car une fois les règles établies, cela va favoriser le développement de la technologie qui pourra alors se faire de manière harmonisée.
Finalement, l’État peut également participer plus concrètement au développement de l’électrification grâce à un apport matériel ou financier, mais également en prenant part directement dans des entreprises privées, ou en nationalisant une partie de l’industrie de développement du réseau électrique.
Il faut cependant noter que des disparités existent entre les pays. Par exemple en France, les départements n’ont que peu de pouvoir sur les infrastructures électriques et s’appuient sur l’état pour leur gestion. À l’inverse les Lander allemands ont une liberté plus importante vis-à-vis de l’État, ce qui leur permet d’intervenir dans l’électrification et l’interconnexion des réseaux au niveau régional[5].
Les acteurs du secteur privé ont également joué un rôle important. En effet les financements privés ont été nombreux lors du développement des réseaux électrique et de leurs interconnexions.
Ainsi les banques et entreprises qui ont fourni des capitaux pour ce développement ont joué un rôle important pour la mise en place du réseau électrique de transport d’électricité triphasé haute tension[6].
Enfin, les gestionnaires de réseaux de distribution (GRD) sont également des acteurs centraux de l’électrification. Ils peuvent êtres publics ou privés, et leur organisation dépend de la structure des réseaux électriques nationaux ou locaux. Ainsi par exemple en France, RTE est le gestionnaire unique du réseau haute tension triphasé, à l’inverse, en Allemagne la gestion est répartie entre 4 GRD.
Les acteurs du réseau de transport et de distribution, et leur organisation influent donc largement sur les choix et politiques de développement de ces réseaux. Ainsi, par exemple, le réseau Allemand est plus largement souterrain que celui de la France, ce qui constitue un investissement financier de départ plus important, et peut donc constituer un frein au développement, mais cela le rend plus fiable sur le long terme. De même de fortes disparités existent au niveau de la surveillance des réseaux de transport et de distribution puisque la France surveille ses réseaux afin d’établir des rapports de disponibilité qui peuvent contribuer à améliorer le développement futur. À l’inverse aucune donnée n’existe pour les réseaux Allemands.
Il apparaît donc bien que les différents acteurs de l’industrie, et des réseaux électriques s’organisent différemment en fonction des localités (pays, régions, etc..), ce qui conduit à des disparités dans la structure, la gestion, et le développement des réseaux de transport et de distribution électrique[7].
Au niveau international (Europe)
[modifier | modifier le code]Une fois les réseaux nationaux établis, la volonté de plusieurs pays européens de mettre en commun leur réseau électrique à permis le développement de réseaux au niveau international.
En effet, l’interconnexion de plusieurs pays à un but économique, stratégique mais également politique en unifiant les pays membres.
Ainsi, après la seconde guerre mondiale, a débuté le développement de lignes haute-tension triphasées transfrontalières, et la création d’un réseau synchrone entre plusieurs pays. Ce développement s’est fait en s’inspirant du modèle américain déjà en place.
Ce réseau européen permet donc aux pays membres d’utiliser un mécanisme de compensation (échanges d’électricité entre pays permettant de compenser la surproduction de l’un, et le déficit de l’autre), mais également de mettre en place des échanges commerciaux d’électricité.
Par exemple, à partir des années 1960, la France développe son parc nucléaire et devient ainsi le premier exportateur d’électricité d’Europe[3].
La carte ci-dessous fait apparaître les différentes zones synchrones existant actuellement en Europe[8].
Définitions de base
[modifier | modifier le code]Grandeurs triphasées
[modifier | modifier le code]Un système de grandeurs triphasées, généralement des tensions ou des courants électriques, peut se décrire par les équations suivantes, où représente le temps.
Systèmes triphasés équilibrés et déséquilibrés
[modifier | modifier le code]Un système de grandeurs (tensions ou courants) triphasées est dit équilibré si les trois grandeurs, fonctions sinusoïdales du temps, ont la même amplitude :
Il est aisé de vérifier qu'en l'occurrence,
Dans le cas contraire, le système triphasé est dit déséquilibré, et cette somme n'est plus nulle.
Pour les tensions et les courants on remplace fréquemment l'amplitude par son expression en fonction de la valeur efficace soit :
- pour les tensions
- pour les courants
Systèmes triphasés directs et inverses
[modifier | modifier le code]Si les trois tensions passent par la valeur 0 dans l'ordre : , , , …, le système triphasé de tensions est dit direct et s'écrit sous la forme :
Si les trois tensions passent par la valeur 0 dans l'ordre : , , , , …, le système triphasé de tensions est dit inverse. Il s'écrit alors sous la forme :
Pour inverser l'ordre des phases, c'est-à-dire passer de l'ordre direct à l'ordre inverse ou réciproquement (par exemple pour inverser le sens de rotation d'un moteur triphasé), il suffit d'inverser le branchement de deux phases.
Tout cela est rigoureusement transposable à un système triphasé de courants.
Distribution triphasée
[modifier | modifier le code]
Une distribution triphasée comporte 3 ou 4 fils :
- Trois conducteurs de phase : la charge est équilibrée, si un courant identique circule dans chacune des trois phases. Tel est le cas, par exemple, des moteurs électriques triphasés.
- Un conducteur de neutre qui n'est pas systématique mais qui est souvent distribué. Lorsqu'un appareil ne consomme pas un courant identique sur chacune des phases, un courant résiduel est produit, que le conducteur neutre permet d'évacuer afin de maintenir la tension nominale de distribution sur chacune des trois branches de la charge.
Pour les installations domestiques de forte puissance (ou pour les immeubles) où l'alimentation électrique se fait en courant triphasé, comme le courant consommé par chacune des phases est en général différent et varie dans le temps (mise en marche d'un lave-linge, d'une cuisinière, allumage et extinction de lumières ou d'appareils électroménagers…), l'installation électrique est généralement déséquilibrée ce qui requiert la connexion du neutre. Si cette dernière devait être défectueuse, certains circuits électriques pourraient recevoir une tension largement supérieure à leur tension nominale, avec des conséquences sérieusement dommageables pour les appareils qui y sont branchés et pour la sécurité de leurs utilisateurs.
Couleur des câbles
[modifier | modifier le code]Les divers conducteurs d'une distribution triphasée peuvent être identifiés grâce à la couleur des câbles qui fait l'objet d'une norme. Malheureusement cette dernière n'est pas internationale et a évolué au cours du temps, ce qui peut être une source de confusion. Il existe des appareils de mesure (testeurs d'installation triphasée) qui permettent de distinguer les différents conducteurs d'une distribution et qui donnent souvent l'ordre des phases.
| L1 | L2 | L3 | Neutre | Terre (ground) / protection par mise à la terre | |
|---|---|---|---|---|---|
| Union européenne et les pays appliquant les standards CENELEC), Hong Kong depuis juillet 2007, Singapour depuis mars 2009 | Brun | Noir | Gris | Bleu | Rayé vert-jaune |
| Ancienne norme européenne (IEC 60446, variable selon les pays) | Noir ou brun | Noir ou brun | Noir ou brun | Bleu | Rayé vert-jaune |
| Normes nord-américaines gérées par la NAERC | Rouge | Noir | Bleu | Blanc | Vert |
Tensions simples
[modifier | modifier le code]Les différences de potentiel entre chacune des phases et le neutre constituent un système de tensions triphasées notées généralement V (V1N, V2N, V3N) et appelées tensions simples, tensions étoilées ou tensions de phase. Dans le cas de distributions équilibrées, l'amplitude des tensions de phase est identique.
En définissant la tension max
pour une distribution équilibrée, cela s'écrit encore
Dans ces équations, ω est la pulsation, φi la phase à l'origine et t le temps.
Dans la plupart des pays européens, la tension efficace de chaque phase est de 230 V nominalement. Sa valeur de crête est alors égale à 325 V.
Tensions composées
[modifier | modifier le code]Les différences de potentiel entre les phases constituent un système de tensions notées généralement U : (U12, U23, U31) et appelées tensions composées ou tensions de ligne.
Les tensions composées constituent un système de tensions triphasées si et uniquement si le système de tensions simples est un système équilibré. La somme des trois tensions composées est toujours nulle. Il en résulte que la composante homopolaire des tensions entre phases est toujours nulle (voir ci-dessous transformation de Fortescue).
Dans le cas de distributions équilibrées, on a :
Relation entre tensions simples et composées
[modifier | modifier le code]
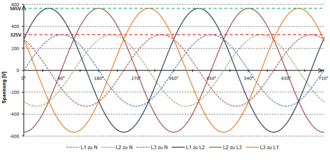
Nous avons reporté sur la figure ci-contre le diagramme de Fresnel des tensions simples et composées délivrées par un système triphasé équilibré direct. L'origine du diagramme représente une tension nulle, celle du neutre. Dans un système équilibré, les tensions simples sont alors celles entre phase et neutre représentées en noir, et les tensions composées celles entre phases représentées en rouge. En observant, par exemple, le triangle isocèle formé par les tensions , et , nous pouvons remarquer que celui-ci a deux angles aigus de radians (soit 30 degrés). On peut ainsi exprimer la valeur efficace de la tension composée en fonction de la valeur efficace de la tension simple à travers la relation (que l'on peut obtenir grâce à la formule d'Al-Kashi) :
Il en va de même dans le cas d'un système équilibré indirect.
Par conséquent, dans un système triphasé équilibré, les valeurs efficaces des tensions simples et composées sont reliées par la relation :
Utilisant la notation complexe, le même résultat est obtenu :
avec
qui lie la tension efficace entre phase et neutre à sa valeur de crête[9].
Récepteurs triphasés
[modifier | modifier le code]Un récepteur triphasé est constitué de trois dipôles aussi appelés phases ou enroulements lorsqu'il est fait référence aux moteurs ou aux transformateurs. Si ces trois dipôles ont la même impédance, et sont donc parcourus par un courant d'amplitude identique, le récepteur est dit équilibré.
Un récepteur triphasé peut être relié à l'alimentation de deux manières :
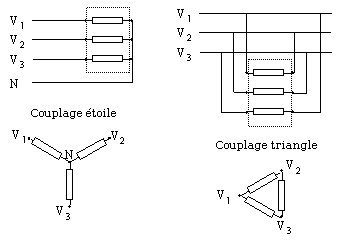
La littérature anglophone désigne habituellement les couplages triangle et étoile par des noms de lettres :
- Triangle : Delta (Δ)
- Étoile : Wye (Y)
Un récepteur équilibré alimenté par un système équilibré de tensions absorbera trois courants de ligne formant également un système triphasé équilibré.
Intensités
[modifier | modifier le code]Les courants de ligne ou courants composés sont notés . Les courants qui traversent les éléments récepteurs sont appelés courants de phase ou courants simples et sont notés .
Connexion d'un récepteur triphasé
[modifier | modifier le code]Les trois dipôles qui constituent le récepteur triphasé sont reliés à six bornes conventionnellement disposées comme l'indique la figure ci-dessous.

L'avantage de cette disposition est de permettre la réalisation des deux couplages avec des barrettes d'égale longueur, la distance entre deux bornes contiguës étant constante. L'appareil est fourni avec trois barrettes identiques dont la longueur permet un câblage horizontal ou vertical. On doit utiliser ces barrettes de connexion afin de réaliser les couplages désirés :
Couplage étoile
[modifier | modifier le code]Le couplage étoile des enroulements (couplage le plus fréquent) s'obtient en plaçant deux barrettes de connexions de la manière suivante :

Les trois bornes restantes seront câblées avec les trois conducteurs de phases.
Les trois bornes reliées ensemble par les deux barrettes constituent un point qui sera au potentiel du neutre. Ce point doit être relié au neutre de la distribution si l'appareil ne présente pas une charge équilibrée, ce qui est le cas par exemple d'une cuisinière électrique. Pour des machines électriques telles que des moteurs triphasés qui présentent une charge équilibrée, on peut faire l'économie du neutre (et donc économiser un conducteur) sans que ses performances ne soient dégradées. Néanmoins, si l'un des pôles varie (usure, mauvais entretien) ou que l'une des phases varie (perturbation sur le réseau de distribution), le moteur présentera un déséquilibre (qui aurait pu être repris par le neutre) qui dégradera les performances du moteur.
Dans un couplage étoile, les courants de ligne et de phase sont les mêmes, aussi on note :
Couplage triangle
[modifier | modifier le code]Le couplage triangle des enroulements s'obtient en plaçant trois barrettes de connexions de la manière suivante :

Un câble de phase est relié ensuite à chaque barrette. Le câble de neutre n'est pas connecté.
Dans un couplage triangle, il est nécessaire de décomposer chaque courant traversant les récepteurs. Ainsi, on a :
Les valeurs efficaces des courants de ligne et de phase sont liés par la relation :
Plaques signalétiques des récepteurs triphasés
[modifier | modifier le code]La plaque signalétique d'un récepteur triphasé précise la valeur de la tension entre phases (tension composée) permettant de l'alimenter.
- Exemple
- chauffe-eau : 230 V/400 V :
- la première valeur est la tension requise pour câbler le récepteur en triangle ;
- la deuxième valeur est la tension requise pour câbler le récepteur en étoile.
Puissance consommée par un récepteur triphasé
[modifier | modifier le code]Puissance active
[modifier | modifier le code]Le théorème de Boucherot impose que cela soit la somme des puissances consommées par chacun des dipôles :
- en étoile : soit, en régime équilibré :
- en triangle : soit, en régime équilibré :
- Pour les récepteurs équilibrés et quel que soit le couplage, on peut écrire : .
Remarque : dans ce cas, n'est pas l'angle de phase à l'origine du temps t = 0 seconde, comme noté précédemment, mais le déphasage entre et . La valeur est appelé facteur de puissance.
Et pour de longs câbles d'alimentation, il est préférable de faire le montage en triangle pour éviter les pics d'intensité dus à la tension réduite d'un montage en Y.
Intérêt du triphasé
[modifier | modifier le code]
Intérêt pour le transport de l'électricité
[modifier | modifier le code]Le transport en triphasé permet d’économiser du câble et de diminuer les pertes par effet Joule : trois fils de phases suffisent (le neutre n'est pas transporté, il est « recréé » au niveau du dernier transformateur). En effet, le déphasage entre deux phases est tel que, pour un système équilibré, la somme des trois courants est supposée nulle (si les trois courants ont la même amplitude, alors ). Et donc, en plus de faire l'économie d'un câble sur les longues distances, on économise en prime sur les effets joule (un câble supplémentaire traversé par un courant impliquerait des pertes supplémentaires).
Par rapport à une distribution en monophasé, à tension entre phases identique et même section de câble, la distribution en triphasé permet de « transporter » une puissance fois plus grande. A contrario, en tenant compte du fil de phase supplémentaire, à puissance et tension entre phases égales, le gain en masse de conducteur est de 15 % (courant de phase réduit de , donc section des conducteurs réduite d'autant, mais trois conducteurs au lieu de deux).
Intérêt pour la production de l'électricité
[modifier | modifier le code]De meilleurs alternateurs
[modifier | modifier le code]L'alternateur triphasé s'est imposé dès l'origine (avant 1900) comme le meilleur compromis[10].
Plus de 95 % de l’énergie électrique est générée par des alternateurs synchrones, des machines électromécaniques fournissant des tensions de fréquences proportionnelles à leur vitesse de rotation. Les alternateurs sont moins coûteux et ont un meilleur rendement que les dynamos, machines qui délivrent des tensions continues (95 % au lieu de 85 %). De surcroît, le courant débité par une dynamo doit être prélevé sur le rotor par le biais d'un collecteur de dimensions imposantes, qui joue encore le rôle d'un redresseur mécanique. Les coûts de construction et d'entretien d'un tel collecteur sont notablement plus élevés que ceux du système de bagues d'un alternateur.
Les alternateurs (machines synchrones) triphasés qui produisent l'énergie électrique ont un meilleur rendement et un meilleur rapport poids/puissance qu'un alternateur monophasé de même puissance.
Annuler la puissance fluctuante
[modifier | modifier le code]Supposons qu'un alternateur monophasé délivre 1 000 A sous une tension de 1 000 V et de fréquence 50 Hz. L'expression de la puissance délivrée se met sous la forme :
Donc la puissance active délivrée (le premier terme de la somme) est comprise entre 0 et 1 MW (elle dépend du facteur de puissance de la charge), mais la puissance fluctuante (le deuxième terme de la somme) est une puissance sinusoïdale de fréquence 100 Hz et d’amplitude obligatoirement égale à 1 MW. La turbine, du fait de son inertie, tourne avec une vitesse mécanique quasi constante, et donc à chaque instant elle fournit une puissance identique. Ces différences de puissance se traduisent par des oscillations de couple[11] qui sont, en majeure partie, absorbées par l’élasticité de l’arbre de transmission et finissent par provoquer sa destruction.
Pour supprimer cette puissance fluctuante, les alternateurs de grande puissance doivent donc nécessairement produire un système de tensions polyphasées : il faut produire n phases (n ≥ 2) déphasées convenablement dans le temps[11].
Par exemple en diphasé :
La puissance fluctuante a bien été annulée.
En régime triphasé équilibré :
En triphasé équilibré, on a trois dipôles identiques, si la tension et le courant varient, la puissance instantanée consommée par un dipôle est égale au produit des valeurs instantanées du courant qui le traverse et de la tension à ses bornes. Pour le générateur ou le récepteur comportant les trois dipôles :
avec p en watts, u en volts et i en ampères.
Considérons, par exemple, un système triphasé direct. En régime sinusoïdal, ces courants et ces tensions ont pour expression :
où Ueff et Ieff sont les valeurs efficaces de la tension et du courant, et φ est le déphasage de la tension par rapport au courant engendré au sein d'un des trois dipôles.
En triphasé équilibré les courants et les tensions ont même amplitudes. De même, les trois dipôles constituant un générateur ou un récepteur étant identique, le déphasage entre tension aux bornes d'un dipôle et l'intensité qui le traverse est lui aussi identique pour chacun des trois dipôles. Cela permet des factorisations dans l'expression de la somme des trois puissances ci-dessous :
La puissance active du générateur ou du récepteur est égale à la somme du produit de ces deux grandeurs. Elle a pour expression :
Or :
La moyenne de puissance instantanée, appelée puissance active, correspond à la puissance réellement consommée par le dipôle. Le second terme de la somme correspond à la puissance fluctuante dont la valeur moyenne est nulle.
La puissance active vaut :
- ,
où cos(φ) est le facteur de puissance.
La « puissance fluctuante » est nulle en régime triphasé équilibré.
Le choix qui a été fait pour l'ensemble des réseaux du monde est n = 3.
Transformation des systèmes triphasés
[modifier | modifier le code]Transformation de Fortescue
[modifier | modifier le code]Notes et références
[modifier | modifier le code]- Jean-Claude Ménégoz, « La logique du développement de l’électricité à l’époque pionnière », Bulletin d'histoire de l'électricité, vol. 12, no 1, , p. 15–23 (DOI 10.3406/helec.1988.1066, lire en ligne, consulté le )
- Éditions Larousse, « révolution industrielle - LAROUSSE », sur www.larousse.fr (consulté le )
- Christophe Bouneau, « Les réseaux de transport d'électricité en Europe occidentale depuis la fin du XIX e siècle : de la diversité des modèles nationaux à la recherche de la convergence européenne », Annales historiques de l’électricité, vol. 2, no 1, , p. 23 (ISSN 1762-3227 et 2272-8023, DOI 10.3917/ahe.002.0023, lire en ligne, consulté le )
- Cours sur le régime sinusoïdal triphasé [PDF] Sur le site www.emc.epfl.ch consulté le 13 avril 2012.
- Pierre Lanthier, « Les autorités publiques et l'électrification, de 1870 à 1940. Une comparaison européenne », Annales historiques de l’électricité, vol. 4, no 1, , p. 125 (ISSN 1762-3227 et 2272-8023, DOI 10.3917/ahe.004.0125, lire en ligne, consulté le ).
- François Caron, « Dynamique des systèmes techniques et «capitalisme» : le cas de l'industrie électrique en France, 1880-1939 », Histoire, économie & société, vol. 19, no 3, , p. 387–410 (DOI 10.3406/hes.2000.2125, lire en ligne, consulté le ).
- « Fiabilité d’approvisionnement, qualité de tension et coûts : Étude comparative des réseaux électriques en Allemagne et en France - Page d'accueil », sur energie-fr-de.eu (consulté le ).
- « Approvisionnement électrique : l'Europe sous tension (rapport) », sur Sénat, (consulté le )
- Olivier Pilloud, Le Radio-amateur : préparation à l'examen technique : manuel de référence, Paris, Éditions Technip, , 540 p. (ISBN 978-2-7108-0902-9, lire en ligne), p. 115.
- CNUM - 8XAE595.2 : p. 120 Sur le site cnum.cnam.fr.
- Christophe Palermo, Précis d'électrotechnique – L'essentiel du cours, exercices et problèmes corrigés, Paris, Dunod, coll. « Sciences sup », 2012, nouveau tirage corrigé 2015, 288 p. (ISBN 978-2-10-058376-8, lire en ligne), chap. 4 (« Systèmes triphasés équilibrés »), p. 159 et suiv.

































































