Théorème d'inversion locale
En mathématiques, le théorème d'inversion locale est un résultat de calcul différentiel. Il indique que si une fonction f est continûment différentiable en un point, si sa différentielle en ce point est inversible alors, localement, f est inversible et son inverse est différentiable.
Ce théorème est équivalent à celui des fonctions implicites, son usage est largement répandu. On le trouve par exemple utilisé, sous une forme ou une autre, dans certaines démonstrations des propriétés du multiplicateur de Lagrange. Il est aussi utilisé pour démontrer le théorème du redressement.
Sa démonstration utilise une version simple du théorème du point fixe. Elle permet d'établir le résultat dans diverses configurations, un espace vectoriel réel de dimension finie, un espace de Banach ou encore une variété différentielle. Il existe une version plus forte : le théorème d'inversion globale.
Énoncés[modifier | modifier le code]
Il en existe plusieurs formes, celle proposée ici est relativement générale[1],[2] :
Théorème d'inversion locale — Soit f une application de U dans F, où U est un ouvert d'un espace de Banach réel et F un espace de Banach et soit x un point de U. Si f est de classe Cp, avec p un entier strictement positif et si la différentielle de f au point x est inversible, alors il existe un ouvert V contenant x et un ouvert W contenant f(x) tels que f se restreigne en une bijection de V dans W dont la réciproque est de classe Cp.
Cet énoncé mérite quelques explications.
- Un espace de Banach est un espace vectoriel normé complet pour la distance induite. Un exemple important est celui des espaces vectoriels réels de dimension finie. Certaines versions limitent d'ailleurs leur énoncé à ce cas particulier[3].
- Une différentielle correspond à la généralisation de la notion de dérivée. Un accroissement f(x + h) – f(x), si h est petit, est presque égal à f'(x).h. A priori, cette égalité possède un sens si f est une fonction de R dans R et le terme f'(x) désigne la dérivée de la fonction f au point x. Si la fonction est définie d'un espace vectoriel dans un autre, ce résultat se généralise mais f'(x).h, qui est alors noté dfx ou Dfx, est une application linéaire continue appelée différentielle de f au point x. L'application qui à x associe Dfx est la différentielle de f ; c'est encore une application d'un espace vectoriel dans un autre, on peut parfois la différentier. Si cette opération est réalisable p fois, et si la différentielle p-ième est continue, l'application f est dite de classe Cp.
- Une application linéaire continue T : E → F entre deux espaces vectoriels normés est dite inversible lorsqu'elle est bijective et que sa réciproque T−1 : F → E (linéaire) est continue. Entre espaces de dimension finie, toute application linéaire est continue. Entre espaces de Banach, d'après le théorème de Banach-Schauder, la réciproque d'une bijection linéaire continue est toujours continue[4].
On dispose du corollaire suivant[1] :
Théorème d'inversion globale — Sous les hypothèses du théorème précédent, si f est de plus injective et si pour tout x de U la différentielle Dfx de f au point x est inversible, alors f(U) est un ouvert et la bijection réciproque, de f(U) dans U, est de classe Cp.
Remarque : Une application bijective de classe Cp dont la réciproque est aussi de classe Cp est appelée un Cp-difféomorphisme.
Approche intuitive[modifier | modifier le code]
Fonction réelle de la variable réelle[modifier | modifier le code]

Le cas de la fonction réelle de la variable réelle est un peu particulier.
Si f est une fonction continue et strictement monotone sur un intervalle J à valeurs réelles, alors f(J) est aussi un intervalle, f est bijective de J sur f(J), et la bijection réciproque est continue (voir l'article Théorème de la bijection). Le graphe de f−1 est le symétrique de celui de f par rapport à la première bissectrice, d'équation x = y, comme illustré sur la figure de droite. Dans le cas particulier d'une fonction réelle de la variable réelle, les résultats sont donc plus globaux et nécessitent des hypothèses de nature différente. Ils ne sont pas généralisables, car un espace vectoriel ne dispose pas d'un ordre à l'image de l'ensemble des nombres réels.
Si de plus f est dérivable en un point a et que cette dérivée en a est non nulle alors f−1 est dérivable au point f(a) (voir l'article Opérations sur les dérivées). Pour cette propriété-ci, par contre, la méthode se généralise parfaitement.
Dimension deux[modifier | modifier le code]
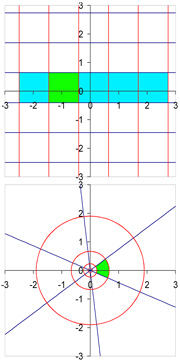
La dimension 2 indique déjà l'existence d'un comportement différent du paragraphe précédent. Illustrons-le pour la fonction f de R2 dans R2 définie par :
La figure de gauche indique comment le plan est transformé. L'image de la figure située en haut est illustrée au-dessous. Le carré vert a été « déformé » de manière bijective. À partir d'un point de l'image du carré vert, il est possible de retrouver le point du carré d'origine. L'application f est de classe C∞ et en tout point, sa différentielle est inversible, car le déterminant jacobien,

n'est jamais nul. L'application est en conséquence localement inversible en chaque point. À la différence des fonctions différentiables et définies sur un intervalle de R, cette propriété n'implique pas le caractère globalement injectif de f. Ajouter 2π à la deuxième coordonnée ne modifie pas l'image par f, ainsi chaque point de R2 possède une infinité d'antécédents, à l'exception de l'origine qui n'en a pas. Cette fonction peut être vue comme l'exponentielle complexe. Sa réciproque, le logarithme complexe, ne peut être définie continûment sur C* tout entier.
Un deuxième exemple est donné par la fonction suivante g, dont le jacobien est égal à x2/2 :
Cet exemple est illustré avec les mêmes conventions sur la figure de droite. La zone bleue en haut à gauche est transformée en une espèce de papillon délimité par deux paraboles. L'application n'est pas inversible au voisinage d'un point ayant une première coordonnée nulle. Intuitivement, il est visible que les deux figures bleues ne sont pas équivalentes : si l'on retranche le point central à celle de droite, la figure comporte alors deux composantes connexes. Le retrait d'un point quelconque sur la figure bleue à gauche ne produit jamais cet effet.
Exemple d'utilisation du théorème d'inversion globale (passage en coordonnées polaires)[modifier | modifier le code]

Soit l'ensemble des de tels que . Soit l'ensemble des points de tels que , et posons . Il est immédiat que et sont des parties ouvertes de . Soit l'application de dans . On a ; en effet, si , on a , donc , donc ; par suite, , ce qui prouve bien que . Il est immédiat que f est injective, et continûment différentiable. Montrons que est surjective. Soit ; posons ; on a , donc il existe un nombre unique dans tel que ; si , on a , ce qui est absurde puisque ; donc ; en outre, , ce qui prouve que est surjective. Le jacobien de en est donc est différent de 0 dans . Donc, d'après le théorème d'inversion globale, est un difféomorphisme de sur , utile en coordonnées polaires.
Usages[modifier | modifier le code]
Les usages du théorème d'inversion locale sont multiples et touchent différentes branches des mathématiques. L'une d'entre elles est la branche d'origine du théorème : la géométrie différentielle. Le théorème d'inversion locale est utilisé soit sous sa forme d'origine, soit sous la forme du théorème des fonctions implicites, qui lui est équivalent au sens où chacun peut se déduire de l'autre.

On utilise le théorème des fonctions implicites pour étudier les figures géométriques définies sous forme d'équations, comme les lignes de niveau d'une fonction de Rn dans R. De manière plus générale, une variété différentielle correspond à la généralisation de courbes ou surfaces régulières, en dimension quelconque. Il existe deux manières de les définir localement, à travers une équation, soit cartésienne, soit paramétrique. Le théorème des fonctions implicites montre l'équivalence de ces deux manières.
En calcul différentiel, le multiplicateur de Lagrange permet de trouver des extrema sous contrainte. Si U est un ouvert d'un espace euclidien, l'objectif est de trouver un extremum d'une fonction f définie sur les points x de U et à valeurs dans R vérifiant l'équation g(x) = 0, où g est une fonction à valeurs dans un autre espace euclidien. Le théorème des fonctions implicites fournit une méthode pour résoudre ce problème.
On trouve encore le théorème d'inversion locale dans les équations différentielles, où il est l'outil de démonstration du théorème du redressement d'un flot. Une équation différentielle explicite possède une forme équivalente à (1) x' = f(t, x). Si la fonction f est indépendante de t l'équation est dite autonome, la fonction est un champ de vecteurs et les solutions de l'équation possèdent des graphes tangents en un point x au vecteur f(x), à l'image de la figure rouge et jaune, à gauche. Le théorème du redressement d'un flot montre que localement, l'équation différentielle est équivalente à celle ayant un champ constant, à l'image de la représentation bleue et jaune, encore à gauche.
Les exemples cités supposent généralement que les espaces vectoriels considérés sont de dimension finie. Tel n'est pas toujours le cas. Une manière d'exprimer les solutions de l'équation (1) est de considérer le flot, c'est-à-dire la fonction α qui, à un instant t et à un point x, associe le point image de la solution s de (1) vérifiant l'égalité s(0) = x. Si la fonction f est de classe Cp, alors le flot α l'est aussi. Une démonstration fait usage du théorème des fonctions implicites dans le contexte d'espaces vectoriels de dimension infinie.
Notes et références[modifier | modifier le code]
- François Laudenbach, Calcul différentiel et intégral, éd. École Polytechnique, , 214 p. (ISBN 978-2-7302-0724-9, lire en ligne), p. 61 et suivantes.
- Pour une démonstration, voir par exemple .
- V&F Bayart, Théorèmes d'inversion locale et globale sur le site bibmath.net.
- Laudenbach 2000, p. 49.
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- J.-F. Ruaud, C. Deschamps et A. Warusfel, J'intègre. Cours de mathématiques de 2e année, Dunod (ISBN 978-2-10-005412-1)
- S. Lang, Analyse Réelle, InterÉditions, Paris, 1977 (ISBN 978-2-72960059-4)





























![{\displaystyle \theta \in ]-\pi ,\pi [,(\theta ,r)\in U}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc2a42c77f2e1ff1a67e7482a918acf0c5809f36)

