Réseau d'antennes
Un réseau d'antennes est un ensemble d'antennes radioélectriques séparées et alimentées de façon synchrone. C'est-à-dire que le déphasage du courant entre deux paires d'antennes est fixe. Un réseau peut comporter des éléments non alimentés directement par une source (éléments parasites), mais par le champ produit par le reste des éléments (c'est le cas des antennes Yagi-Uda). Le champ électromagnétique produit par un réseau d'antennes est la somme vectorielle des champs produits par chacun des éléments. En choisissant convenablement l'espacement entre les éléments et la phase du courant qui circule dans chacun, on peut modifier la directivité du réseau grâce à l'interférence constructive dans certaines directions et à l'interférence destructive dans d'autres directions.
Rayonnement d'une paire d'antennes[modifier | modifier le code]

Soient deux antennes identiques séparées d'une distance et alimentées en phase (c'est-à-dire, déphasage des courants nul).
Calculons le champ électrique produit par cette paire d'antennes à une distance très grande des antennes. C’est-à-dire que est très grand comparée à la longueur d'onde et que . Comme la distance est grande, l'angle est le même pour les deux antennes et le champ produit par chacune sera aussi le même : et . Mais si l'amplitude est la même, la phase ne le sera pas, parce que l'antenne 2 est plus proche du point de mesure que 1. Le champ produit par l'antenne 2 arrivera secondes plus tôt que le champ produit par l'antenne 1. Autrement dit, le champ produit par l'antenne 2 sera en avance de phase de :
Ici, est le nombre d'onde.
Comme les deux champs sont parallèles, la somme vectorielle se réduit à additionner les amplitudes, mais en tenant compte du déphasage :
Comme la phase du champ électrique reçu ne présente aucun intérêt et que seule l'amplitude est importante, seul le module de ce nombre nous intéresse :
Il est facile de constater que pour , le champ électrique est maximal et égal au double du champ produit par chacune de deux antennes. Ceci est logique car pour , les deux émissions ont parcouru la même distance et arrivent en phase. Par contre, le champ émis sera zéro quand le cosinus vaudra zéro. ceci arrive la première fois quand . C'est-à-dire, quand la différence de distance parcourue est égale à la moitié d'une longueur d'onde et que les deux émissions arrivent avec un déphasage de 180°. Quand augmente, la différence de distance parcourue augmente et la phase va vers 360° et pour cette valeur nous aurons un nouveau maximum. Chaque fois que est égal à un multiple impair de l'émission passe par zéro et chaque fois que est égal à un multiple pair de l'émission est maximal. Mais il ne faut pas oublier que ne peut pas augmenter indéfiniment car sa valeur est comprise entre -90° et +90°.
Il ne faut pas oublier, non plus, que l'émission est symétrique autour de l'axe qui passe par les antennes.
Les antennes ont un diagramme d'émission propre. Le champ que nous avons calculé ne tient compte que de l'aspect interférence entre les deux ondes émises par chacune des antennes. Dans le calcul et la visualisation du résultat final il faut tenir aussi compte du diagramme de rayonnement des antennes. Par exemple, le calcul que nous venons de faire peut donner un maximum pour , mais si les antennes sont des dipoles alignés avec l'axe des antennes, le résultat final ne sera pas un maximum pour , mais un zéro, car les dipôles n'émettent pas dans cette direction.
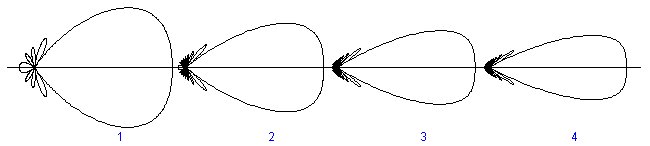
Voici un exemple formé par deux antennes dipôle verticales séparées par une distance

À gauche, nous avons dessiné le diagramme de rayonnement d'un dipôle . Au centre, le diagramme de rayonnement dû aux interférences entre les deux antennes. Le diagramme de rayonnement résultant est à droite et est le résultat de multiplier les deux diagrammes précédents. Les trois dessins sont symétriques autour de l'axe vertical.
Réseau d'antennes à émission transversale[modifier | modifier le code]

Soient n sources alignées alimentées en phase séparées par une distance entre chacune. Examinons le champ lointain rayonné dans la direction . En prenant comme référence de phase celle du champ lointain de l'élément rayonnant 1 (en anglais : radiator), , le champ lointain de l'élément rayonnant 2 aura une avance de phase de . L'élément rayonnant numéro 3 aura une avance de phase de et de même pour les suivants. Pour calculer le champ total, il suffit d'ajouter tous les champs en tenant compte du déphasage. Comme toutes les amplitudes sont égales :
mais nous connaissons la somme d'une série géométrique :
Comme seule l'amplitude nous intéresse, la première fraction disparaît. Utilisant la Formule d'Euler nous pouvons écrire :
- .
présente des maximums et des zéros en fonction de , et donc, en fonction de . Mais ces maximums n'ont pas tous la même valeur. Le premier vaut . Les suivants sont plus petits et leurs valeurs dépendent de . Le premier zéro arrive pour . C'est-à-dire, quand . Comme Nous retrouvons une relation similaire à celle que nous avions calculée pour deux antennes : le premier zéro apparait quand les déphasages de chacune des antennes sont uniformément distribués entre 0° et 360° (0 et radians en unités scientifiques). Le prochain zéro apparaîtra quand les déphasages seront distribués uniformément entre 0° y 720° (0 et radians), etc.
Dans la figure suivante nous avons tracé les diagrammes de rayonnement de quelques cas particuliers. Seul l'aspect interférence a été dessiné. Pour obtenir le diagramme de rayonnement définitif, il faudrait multiplier ces diagrammes par le diagramme de rayonnement des émetteurs individuels. Dans le dessin les réseaux d'antennes sont verticaux.
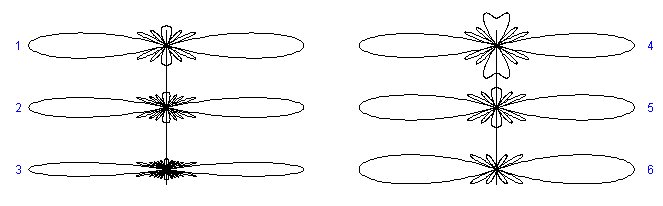
| Diagrammes de rayonnement d'un réseau d'antennes isotropes à émission transversale. | |||
| Numéro du diagramme | Nombre d'antennes | Séparation entre antennes | Longueur totale |
| 1 | 7 | ||
| 2 | 9 | ||
| 3 | 17 | ||
| 4 | 5 | ||
| 5 | 7 | ||
| 6 | infini | ||
Les diagrammes de gauche montrent l'influence de la longueur totale du réseau. Quand la longueur du réseau augmente, la largeur du lobe principal diminue et les lobes secondaires se font plus nombreux et plus petits. Les diagrammes de droite montrent l'influence d'augmenter le nombre d'antennes en conservant la même largeur du réseau. Quand le nombre d'éléments augmente, l'amplitude des lobes secondaires diminue, mais ne tend pas vers zéro.
Réseau d'antennes à émission longitudinale[modifier | modifier le code]
Dans le réseau d'antennes à émission transversale le lobe maximal d'émission se situe dans un plan "équatorial" parce que, dans ce plan et loin du réseau, chaque point est situé à la même distance de chacune des antennes.
Imaginons que cette fois nous alimentons chaque antenne avec un retard de phase par rapport à sa voisine d'en bas. Dans ce cas, pour recevoir toutes les émissions en même temps (en phase), au lieu de rester sur le plan équatorial, il faudra se placer un peu plus haut, pour diminuer la distance vers les antennes du haut. Le plan du lobe principal s'est transformé en une surface conique dont le sommet est situé sur le réseau. Si nous augmentons le retard de phase, le cône du lobe principal se refermera et il arrivera un moment où le cône sera complètement fermé et transformé en une droite alignée avec les antennes. Pour arriver à cette situation il faut que le retard de phase de chaque antenne corresponde au temps que l'émission de l'antenne d'en bas met pour arriver. Si la distance entre les antennes est , le retard de phase sera . La formule de est la même que celle du cas précédent. La seule différence est que cette fois il faut diminuer l'angle de :
On peut constater que pour (90°) le déphasage est zéro.
Voici quelques exemples de diagramme de rayonnement d'un réseau d'antennes à émission longitudinal. Les antennes sont alignées horizontalement. Comme dans la figure précédente, le dessin ne tient compte que du seul aspect des interférences. Pour obtenir le diagramme final, il faudrait multiplier chaque diagramme par le diagramme d'émission de chaque antenne individuelle.
Réseau bidimensionnel d'antennes[modifier | modifier le code]
Les réseaux bidimensionnels d'antennes furent très utilisés il y a quelques décennies pour faire des émissions directionnelles dirigées horizontalement en ondes courtes. Ces communications servaient à communiquer avec d'autres continents ou avec des navires en mer. Bien entendu, avec l'utilisation des satellites de communication, la communication commerciale par des ondes courtes et les énormes réseaux d'antennes nécessaires sont disparus et nous n'en parlerons pas.
Maintenant un autre type de réseau bidimensionnel d'antennes est utilisée. Ce sont les antennes utilisées surtout dans les radars à balayage (phased arrays en anglais). Comme nous verrons, ce type d'antenne permet d'orienter le faisceau du radar sans déplacer mécaniquement l'antenne.
Les réseaux bidimensionnels d'antennes actuelles sont formés par quelques milliers d'émetteurs individuels disposés en réseau bidimensionnel carré, rectangulaire ou, plus souvent, hexagonal. Pour comprendre le principe de fonctionnement, imaginez un réseau d'émetteurs formant un réseau carré sur l'écran de votre ordinateur.

Si vous êtes placé loin de l'écran, et que tous les émetteurs sont alimentés en phase, pour recevoir toutes les émissions en phase vous devez vous placer dans la perpendiculaire à l'écran qui passe par le réseau. Maintenant changeons la phase de l'alimentation des émetteurs de façon que chaque émetteur soit en avance de phase par rapport à son voisin de droite (la vôtre). Pour recevoir tous les émetteurs en phase et ainsi rester sur l'axe du faisceau vous devrez vous déplacer vers vôtre droite, pour vous éloigner des émetteurs qui émettent avec avance de phase.
De la même façon, si nous voulons que le faisceau principal aille vers le haut, nous devons avancer la phase de chaque émetteur par rapport à son voisin d'en haut.
Un réseau bidimensionnel peut être considéré comme un réseau linéaire dont les émetteurs sont des réseaux linéaires à émission transversale.
Ainsi, si chaque émetteur individuel a un diagramme d'émission du type dans lequel et sont, par exemple, l'azimut et l'élévation, une ligne d'émetteurs produira un champ de cette forme :
Où est le facteur dû à l'interférence des émetteurs d'une ligne. Maintenant considérons chaque ligne comme un élément de la colonne. Si est le facteur dû à l'interférence de émetteurs de la colonne, le diagramme total sera:
Nous n'irons pas plus loin dans le calcul des facteurs . Dans cet article vous pouvez trouver des formules plus détaillées. Examinons l'aspect de l'émission de ce type d'antenne. Dans le cas d'un réseau rectangulaire, le lobe principal aura un premier zéro pour un angle tel que
Où est la longueur d'onde et es la largeur de l'antenne dans la direction dans laquelle nous mesurons . Si le réseau est circulaire la formule précédente devient :
Cette fois, est le diamètre du réseau.
Ces formules sont valables quand le faisceau est perpendiculaire au réseau. Si les déphasages donnés font que le faisceau est incliné d'un angle par rapport à la perpendiculaire, le diamètre effectif du réseau se trouve réduit d'un facteur , ce qui a pour effet d'élargir le lobe principal. Ceci limite les angles utiles du réseau bidimensionnel. Pour couvrir la voûte céleste il faut trois émetteurs avec des orientations à 120°.
L'intérêt de ce type de réseau est que, si on équipe chacun des quelques milliers d'émetteurs d'un dispositif individuel qui retarde l'émission (et la réception), on peut changer la direction dans laquelle "tire" l'antenne en quelques microsecondes à la place de secondes ou dixièmes de secondes nécessaires pour orienter mécaniquement une parabole. Évidemment, le retard de chaque dispositif est calculé et contrôlé par ordinateur. Ceci permet au radar (militaire, bien sûr) de surveiller et traiter plusieurs cibles simultanément. Les utilisations sont surtout militaires : radars d'avions et navires militaires et des radars de systèmes anti-missiles utilisées dans les versions actuelles de la Guerre des étoiles. Au moins une application civile utilise ce type d'antenne. Il s'agit du réseau de téléphone satellite Iridium. Les antennes de ces satellites concentrent l'émission et réception dans une petite zone sous le satellite. Celui-ci balaye la petite zone sur une étendue beaucoup plus grande plusieurs milliers de fois par seconde.
Un autre intérêt de ce type d'antenne est que, comme il y a des milliers d'émetteurs, chacun n'émet que quelque dix-millièmes de la puissance totale, ce qui fait que les circuits retardateurs travaillent à puissance relativement réduite.
Pour calculer le retard à donner à chaque émetteur, il faut calculer la différence de chemin à parcourir entre les signaux de l'émetteur donné et celles de l'émetteur de référence. Cette distance est la projection du segment qui relie les deux émetteurs sur la droite dirigée vers la direction souhaitée du faisceau. Pour calculer cette projection on peut faire le produit scalaire du vecteur qui va de l'émetteur donné à l'émetteur de référence, par le vecteur unitaire parallèle à la direction souhaitée.
Problèmes pratiques propres aux réseaux d'antennes[modifier | modifier le code]
Dans tout ce qui a été dit précédemment, nous avons gardé sous silence l'interaction entre antennes.
L'interaction entre éléments individuels induit des courants dans les autres éléments ce qui modifie l'impédance de l'élément, ce qui peut modifier la phase du courant d'alimentation. Ceci fait que fixer la phase de chaque élément quand les éléments interagissent est extrêmement compliqué. Une façon de contourner le problème est d'alimenter un seul élément. De cette façon la phase du courant des autres éléments est fixée par la seule géométrie du réseau. C'est la solution utilisée dans les antennes Yagi-Uda. Une autre façon d'éviter les interactions est de choisir le type d'antenne individuelle et sa disposition. Ainsi, si on utilise des antennes dipolaires, on peut les disposer alignées, car ces antennes n'émettent pas dans le sens de leur longueur. Une autre possibilité est celle d'utiliser des antennes individuelles qui ne rayonnent pas dans la direction des autres antennes du réseau. C'est la solution utilisée dans les "phased arrays".
Impédance mutuelle et interaction entre antennes[modifier | modifier le code]
Le courant qui circule dans chaque antenne induit des courants dans toutes les autres. Aussi bien si les autres sont alimentées ou non. On peut postuler une impédance mutuelle qui jouera le même rôle dans les antennes que l'inductance mutuelle dans les bobines couplées. L'impédance mutuelle entre deux antennes est définie comme
où est le courant qui circule dans l'antenne 1 (inductrice) et est la tension qu'il faudrait appliquer à l'antenne 2 (induite) – avec l'antenne 1 enlevée – pour obtenir le même courant dans l'antenne 2 que celle induite par le courant de l'antenne 1.
Avec cette définition, l'ensemble de courants et de tensions d'un ensemble d'antennes est relié par le système d'équations suivant :

où :
- est la tension appliquée à l'antenne
- est la impédance de l'antenne
- est l'impédance mutuelle entre les antennes et
Remarquez que, comme pour les inductances mutuelles :
Si quelques éléments ne sont pas alimentés (il y a un court-circuit à la place du câble d'alimentation), comme c'est le cas dans les antennes Yagui-Uda les correspondants sont zéro. Ces éléments reçoivent l'injuste nom d'éléments parasites. Dans certaines configurations géométriques, l'impédance mutuelle entre deux antennes peut être zéro. C'est le cas pour des dipôles disposés en croix (dans les antennes à émission ou réception polarisée circulairement). Ces impédances nulles facilitent le calcul et surtout, la réalisation.
Références[modifier | modifier le code]
- (en) F.R. Terman, Electronic Radio and Engineering, MacGraw-Hill